1257951430

96

pokazano na rys. 7.3a. Czas inkubacji do osiągnięcia przez szczelinę jej krytycznego rozwarcia 5* może być określony z zależności:

(7.28)

lub ogólnie (7.29) gdzie: p, a - stałe materiałowe.

Wyznaczenie czasu inkubacji na podstawie powyższych zależności wymaga wyznaczenia dwóch stałych materiałowych, a w szczególności krytycznego rozwarcia szczeliny 5_r

Przy znajomości krzywej pełzania dla naprężenia równego naprężeniu bazowemu Gr elementu z pęknięciem czas inkubacji może być wyznaczony

graficznie. Czas ten jest równy okresowi, po którym odkształcenie pełzania

osiągnie wartość krytyczną ef definiowaną jako:

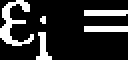
5. \l/(el + 1)

(7.30)

lub w formie konserwatywnej:

5. W(n + 1)

(7.31)

Oprócz omówionego powyżej procesu zaokrąglania wierzchołka szczeliny, w okresie inkubacji może zachodzić proces rozbudowy obszarów zniszczenia i mikrowzrostu szczeliny. Jako czas inkubacji przyjmuje się wzrost szczeliny o wielkość równą rozmiarowi ziarn r_c. Dolna i górna granica okresu inkubacji mogą być wtedy wyznaczone z zależności

(7.32)

(7.33)

(n + l)r_c£f

3C*°,85

gdzie: r_c - wyrażono w mm, t, w godzinach, C w MJ/m h, £f jest bezwymiarowym maksymalnym odkształceniem pełzania.

7.2.2. Propagacja pęknięć przy obciążeniach stałych

Wyniki badań doświadczalnych wskazują, że proces propagacji pęknięcia może być opisany ogólną zależnością typu [48, 53]

4^ = D C*^<p    (7.34)

dt

gdzie: D, <p - stałe materiałowe.

Na podstawie rozważań pola naprężeń w obszarze zniszczenia wokół wierzchołka pęknięcia w pracach [135, 137] podano następujące zależności analityczne do obliczenia stałych D i cp

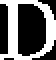
n + 1
	£f()	InGi£0

_r(n+ 1 - v)(n + 1)

(7 35)

(7.36)

(p = v/(n + 1)

gdzie:

g₀, e₀, n, v - stałe materiałowe,

^efo maksymalne odkształcenie pełzania przy naprężeniu Gq, r_c - rozmiar strefy zniszczenia.

Powyższą zależność dla płaskiego stanu naprężenia można aproksymować następującą prostą formułą [95]

da

dt

(7 37)

gdzie:

da

dt

wyrażone jest w mm/h, C w MPam/h.

W płaskim stanie odkształcenia odpowiednikiem równania (7.37) jest zależ

ność

da

dt

150C*^0,85

(7 38)