1388457465

56

Andrzej Szlęk

J

równanie (8.11) przyjmuje ostatecznie postać:

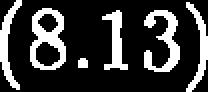
^A9^wgP_S

+

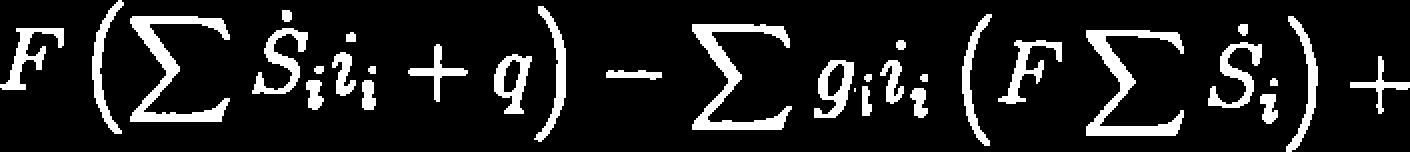
dT,

dx

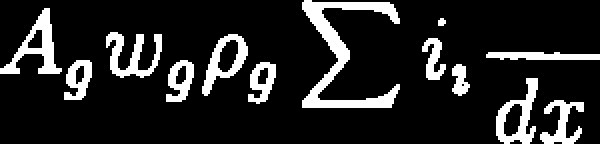
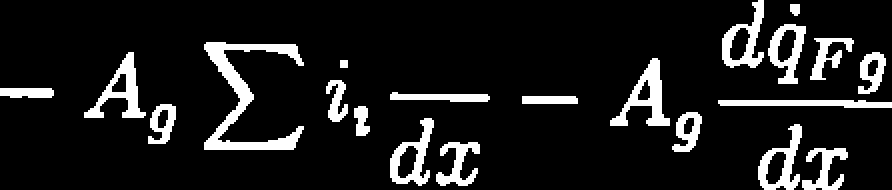
Z równania (8.13) można wyznaczyć pochodną temperatury fazy gazowej po wysokości złoża.

Przedstawione równania stanowią komplet równań umożliwiających określenie zmian temperatury i składu fazy gazowej wzdłuż wysokości złoża. Z równań postaci (8.9) wyznacza się pochodne udziałów gramowych -f*, na-

E3*

stępnie z równania (8.13) pochodną temperatury fazy gazowej W dalszej kolejności z równania (8.5) wyznacza się pochodną gęstości i ostatecznie z równania (8.3) pochodną prędkości. Wymienione równania stanowią układ równań różniczkowych sztywnych [15], których rozwiązanie wymaga stosowania specjalnych procedur, co niestety znacznie wydłuża czas obliczeń. Dodatkowo w równaniach tych, w członach dyfuzyjnych, występują w sposób

niejawny drugie pochodne udziałów gramowych oraz temperatury, co dodatkowo komplikuje rozwiązanie układu.

Autor niniejszej pracy zdecydował się rozwiązać przedstawiony układ metodą iteracyjną, biorąc do obliczeń wartości strumieni dyfuzyjnych obliczonych w poprzednim kroku iteracyjnym. Dokładniejszy opis zastosowanej metody rozwiązywania przedstawiono w dalszej części pracy.

8.3. Równania opisujące zmiany parametrów fazy stałej

W stanie ustalonym paliwo dopływa w sposób ciągły do dolnej części złoza i przesuwając się ku górze ulega wypaleniu wskutek wymiany substancji oraz energii z fazą gazową. Zmiany składu fazy stałej wynikają ze zjawiska

Mo del matem atyczny    ___

odgazowania i zgazowania, natomiast zmiany temperatury wynikają z dyfuzji ciepła w fazie stałej, wymiany ciepła z fazą gazową oraz ciepła reakcji zgazowania. Dla fazy stałej zapisać można równania bilansu całości masy, karbonizatu, i-tej części lotnej oraz energii. Poniżej przedstawiono postać

poszczególnych równań.

Bilans masy. Strumień masy, który obliczony może być jako A_sw_sp_s, zmienia się w wyniku odpływu od fazy stałej do gazowej strumieni masy związanych z odgazowaniem i zgazowaniem, co można ująć równaniem.

d{A_aw_aPaJ ₌ __{F Gi} + D\ _s    (8.14)

dx    '

w którym:

A_s - powierzchnia przekorju fazy stałej, m², w_s - prędkość fazy stałej, m/s, p_s - gęstość fazy stałej, kg/m³>

Gi - gęstość strumienia odgazowania i-tej substancji, kg/(m²s)j D_c - gęstość strumienia zgazowywanego pierwiastka węgla, kg/(m²s).

Bilans sumy części lotnych. Jakkolwiek części lotne w rozumieniu związków chemicznych tworzone są w wyniku pirolizy substancji węgla, to dla celów modelowania przyjąć można, że występują one w węglu w postaci związków uwalnianych do fazy gazowej wraz z nagrzewaniem paliwa. W takim przypadku bilans sumy części lotnych zapisać można jako:

d{A_aWsp_ay_v) ₌ __f^q.    (8.15)

i    Zu * ⁵

dx

przy czym symbolem y_u oznaczono gramowy udział części lotnych w paliwie. Wykonując w powyższym równaniu różniczkowanie względem wysokości złoża uzyskuje się następujący wynik:

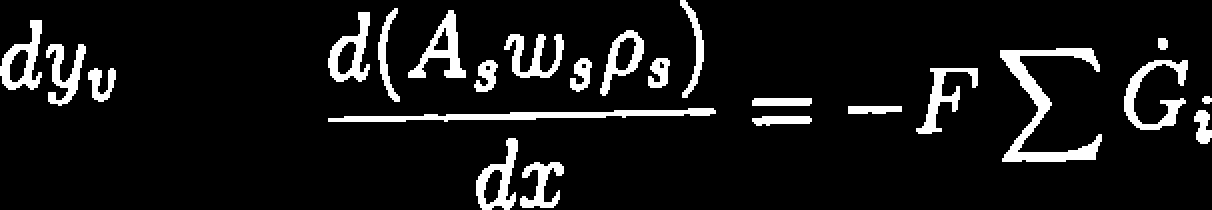
(8.16)