2150625544

(22)

8. Kryza pomiarowa

Na podstawie prawa przepływu Bemouliego:

p u²

—l--= C = const

P 2

dla kryzy pomiarowej umieszczonej w rurociągu (rys.2.1) można napisać:

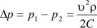
(23)

Na stanowisku laboratoryjnym mierzy się bezpośrednio charakterystykę Ap = /(u) za pomocą kryzy pomiarowej - różnicę ciśnień p\ i pi jako funkcja średniej prędkości przepływu gazu przez rurociąg u. Jeśli kryza pomiarowa będzie przy tej charakterystyce wywzorcowana to będzie mogła służyć jako przepływomierz przy czym zwykle wystąpi konieczność wyznaczenia jej charakterystyk pośrednich: Ap = f{Q_v) lub Ap = f{Q_m).

Z zależności (23) wynika że, w wyniku przepływu płynu o gęstości właściwej p przez przewężenie (kryza) powstaje różnica ciśnień Ap proporcjonalna do kwadratu prędkości przepływu płynu. Jest to zależność dla idealnego przepływu. W rzeczywistości kryza pomiarowa zmienia charakter przepływu (przed kryzą następuje spiętrzenie płynu i wzrost ciśnienia (p\ > p) a za kryzą spadek ciśnienia (p2 < p). Ponadto za kryzą powstają zawirowania przepływu. Przepływ za kryzą nie jest laminamy ale burzliwy (turbulentny). W przypadku rzeczywistym wartość C = Cr jak w zależności (23) nie jest stała. Zależy ona od prędkości przepływu u, charakteru przepływu (liczby Reynoldsa Re - dla przepływu burzliwwego Re >2000) współczynnika przewężenia kryzy P = d/D a także od stopnia rozprężenia płynu za kryzą - liczba ekspansji s.

Przepływ masowy Q_m mierzony za pomocą kryzy w warunkach rzeczywistych opisuje zależność:

(24)

przy czym:

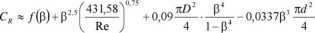
/(P) = 0,5959 + 0,0312P²¹ - 0.184P³;

(25)

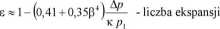
(26)

C

k =--wykładnik adiabaty (dla powietrza k = 1,4)

^{e =}/(Pi A/>/p\) - wartość można odczytać z wykresu dla określonej

zwężki np. kryzy o danej wartości P; N_q - liczba przepływu;

4p Q_v

Re =--liczba Reynoldsa

nDr\

(27)

w warunkach normalnych (p₀⁼101,33kPa; 7'₀=273,15K) dla powietrza można przyjąć:

(28)

MT ćw. 1 Pomiary przepływu

14