3071579908
Równania stanu - dyskretyzacja modeli (uproszczenia)

Jeżeli xq = 0, to szereg ten nazywamy szeregiem Maclaurina. Rozwinięcie funkcji w szereg Maclaurina ma następującą postać
f(x) = f(0) + f)^x" (34)
0=1
Dla funkcji wykładniczej, szereg Maclaurina ma postać
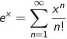
(35)
Wyszukiwarka
Podobne podstrony:
Równania stanu - dyskretyzacja modeli (uproszczenia) Postępowanie to odwołuje się do transformacji T
Równania stanu - dyskretyzacja modeli (uproszczenia) W praktyce do realizacji w czasie rzeczywistym
Równania stanu - dyskretyzacja modeli (uproszczenia) Model z czasem ciągłym 0 1 0 ■ 0
Równania stanu - dyskretyzacja modeli Chcąc zaprojektować układ regulacji w technice mikroprocesorow
Równania stanu - dyskretyzacja modeli Transformacja ciągłych równań różniczkowych do dyskretnych
Równania stanu - dyskretyzacja modeli Równanie stanu modelu przekształca się, zgodnie z zasadami
Równania stanu - dyskretyzacja modeli W przypadku modelu opisanego pulsacją drgań swobodnych ujq i
Równania stanu - dyskretyzacja modeli Ostatecznie otrzymuje się model z czasem dyskretnym: / X(k + 1
1.12 Napisać macierzowe równanie stanu układu liniowego f x(t) = Ax(t) + Bu(t), x(to) = xq y{t) =
Może to być np. długość łuku OP = L, wówczas z równania naturalnego L * R — a2 określimy promień R.
więcej podobnych podstron