3547343767

11

Egzamin maturalny z matematyki Kryteria oceniania odpowiedzi poziom podstawowy

Zdający otrzymuje............................................................................................................2 pkt

gdy poprawnie wyznaczy równanie symetralnej odcinka^#: x + 2_y-12 = 0 lub

1 .

y = —x + 6.

2

111 sposób rozwiązania

Z rysunku w układzie współrzędnych

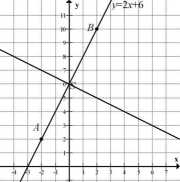
odczytujemy współrzędne punktu S = (0,6), współczynnik kierunkowy symetralnej odcinka AB: a = —^ * zapisujemy równanie symetralnej odcinka/IZ?: y = -^x+6.

Schemat oceniania III sposobu rozwiązania

Zdający otrzymuje............................................................................................................1 pkt

gdy odczyta, z dokładnie sporządzonego rysunku w układzie współrzędnych, współrzędne środka odcinka AB i współczynnik kierunkowy symetralnej prostej AB i na tym poprzestanie lub dalej popełni błędy.

Zdający otrzymuje............................................................................................................2 pkt

gdy zapisze równanie symetralnej odcinka/4Z?: x + 2_y-12

0 lub y

6.

IV sposób rozwiązania

Korzystamy z tego, że symetralna odcinka jest zbiorem wszystkich punktów równo oddalonych od jego końców. Jeśli punkt P = (x,y) leży na symetralnej, to \AP\ = \BP\.

Zatem    , czyli (x+2f +(y-2)² = (x-2f +(y-10)^!.

Po uporządkowaniu równania i redukcji wyrazów podobnych otrzymujemy x + 2y-\2 = 0.

Schemat oceniania IV sposobu rozwiązania

Zdający otrzymuje............................................................................................................1 pkt

gdy zapisze równanie tJ(x + 2)² + {y- 2)¹ = y](x-2)² +(y-10)² i na tym poprzestanie lub dalej popełni błędy.

Zdający otrzymuje............................................................................................................2 pkt

gdy wyznaczy równanie symetralnej odcinka AB: x+2y-\2 = 0 lub >■ = -—x + 6.