3547343770

14

Egzamin maturalny z matematyki Kryteria oceniania odpowiedzi - poziom podstawowy

Schemat oceniania 1 i II sposobu rozwiązania

Zdający otrzymuje............................................................................................................1 pkt

gdy

•    obliczy liczbę wszystkich możliwych zdarzeń elementarnych: |fi| = 7² = 49 albo

•    obliczy (zaznaczy poprawnie w tabeli) liczbę zdarzeń elementarnych sprzyjających zdarzeniu A : \A\ = 17 .

Zdający otrzymuje............................................................................................................2 pkt

gdy obliczy prawdopodobieństwo zdarzenia A\ P(A) - 22 Uwaga

Jeśli zdający rozwiąże zadanie do końca i otrzyma P(A) > 1, to otrzymuje za całe rozwiązanie 0 punktów.

III sposób rozwiązania {metodadrzewa) Drzewo z istotnymi gałęziami:

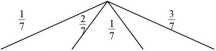
6	2,	4	3	1,5,7
’ / Dowolna z siedmiu	3,	1 6	^ł \ 2,4,6	^ł\ 6

Prawdopodobieństwo zdarzenia A (iloczyn wylosowanych liczb jest podzielny przez 6)

jest więc równe: P(A) =

I Z

7 7

2 2 7 7

I    ł 2 i

II    ii

17

49'

Schemat oceniania III sposobu rozwiązania

Zdający otrzymuje............................................................................................................1 pkt

gdy:

•    narysuje pełne drzewo i przynajmniej na jednej gałęzi opisze prawdopodobieństwo albo

•    narysuje drzewo tylko z istotnymi gałęziami.

Zdający otrzymuje............................................................................................................2 pkt

17

gdy obliczy prawdopodobieństwo zdarzenia/4: P(A) = —.

Jeśli zdający rozwiąże zadanie do końca i otrzyma P(A) > 1, to otrzymuje za całe rozwiązanie 0 punktów.

Kryteria oceniania uwzględniające specyficzne trudności w uczeniu się matematyki

Jeżeli zdający poprawnie obliczy prawdopodobieństwo i błędnie skróci ułamek, 17    1

np. P(A) = — = -, to otrzymuje 2 punkty.