5783291271

Kinematyka

Punkt Sjest chwilowym środkiem obrotu dla wodzika AB (rys. 2.14). Możemy zatem wyznaczyć prędkość kątową wodzika co:

v. 20    . _    , .

co = —— = — = 0,5 rad/s

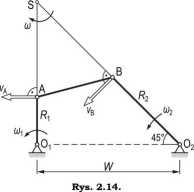
Prędkość punktu B jest równa:

v_B = a BS = 0,5 • 20(3V2 - 2) = 10(3^2 - 2) * 22,426 cm/s Znając prędkość punktu B, możemy wyznaczyć prędkość kątową korby O2B:

0,561 rad/s

10(3^2-2) 3J2-2

Wyznaczanie przyspieszeń poszczególnych punktów rozpoczynamy od punktu A. Korba OiA jest w ruchu obrotowym ze stałą prędkością co\, dlatego w punkcie A wystąpi tylko przyspieszenie normalne a_A :

a_A = a_A = a% • O_łA = oj² •    - (l)² • 20 = 20 cm/s²

Przyspieszenie punktu B jest równe (rys. 2.15):

~ ® A ®BA ®B ⁼ ® A ^BA Oba

gdzie:

a_A = 20 cm/s²

^aB - ^a2 ‘ ^2^ =    ■ R2

’3,/2- 2 J

• 40 = 5(11 - 6V2)«12,574 cm/s²

^aBA = w² ■ AB - (0,5)² • 2oVl4-8c/2 = 5Vl4-8i/2 * 8,195 cm/s²

Zrzutujmy wektory zaczepione w punkcie B na kierunek przyspieszenia normalnego dg i stycznego dg . Otrzymujemy:

— na kierunku przyspieszenia normalnego dg :

^aB - ^aA ’ cos(45°) - dg_A • sin(45° - fi) + dg_A ■ cos(45° - /3)