7193935653

Krzysztof Kęcik

wniosek można wyciągnąć, analizując wpływ tłumienia

MR (rys. 7).

Zmiana temperatury może powodować wzrost lub obniżenie amplitudy drgań wahadła w porównaniu do układu z liniową charakterystyką sprężyny (tys. 10).

3.2 DYNAMICZNA ELIMINACJA DRGAŃ

W poprzednim podrozdziale wykazano, że efekt dynamicznej eliminacji drgań jest nąjkorzystniejszy przy częstości wymuszenia 8 = 0.7. Na rys. 11 (oscylator) oraz 12 (wahadło) przedstawiono analizę bifurkacyjną rozwiązania okresowego, przy tej częstości, pod wpływem tłumienia MR. Szare punkty oznaczają badania doświadczalne, linie ciągłe i przerywane oznaczają odpowiednio stabilne i niestabilne rozwiązalne nume-

Wartością graniczną, przy której wahadło przestaje wykonywać ruch, jest a₃ — 0.5. W warunkach dynamicznej eliminacji drgań, aktywowanie tłumienia MR pozwala obniżyć drgania oscylatora z poziomu 1.35 do 1.15 (ok. 15%, rys. 11). W badaniach doświadczalnych uzyskano ok. 7% redukcji drgań. Wraz ze wzrostem wartości tłumienia MR spada wartość amplitudy drgań samego oscylatora (tzw. rozwiązanie pól-trywialne). Zmieniając wartość parametru oc₃. można również dobierać amplitudę drgań wahadła (rys. 12).

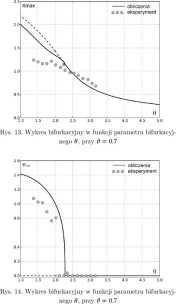
Wpływ temperatury sprężyny SMA na efekt dynamicznej eliminacji drgań jest przedstawiony na wykresie bifurkacyjnym (rys. 13). Graniczna wartość temperatury przy której wahadło przechodzi do spoczynku 8 w 2.2, tzn. aktywowana temperatura równa jest 2.2T>i (gdzie Tm jest temperaturą przemiany martenzytycznej). Spadek amplitud oscylatora rozwiązania trywialnego jest praktycznie taki sam jak rozwiązania liietrywialnego (obie linie są równolegle, rys. 13).

Natomiast zastosowanie sprężymy SMA w warunkach dynamicznej eliminacji drgań pozwala obniżyć drgania oscylatora o ok. 35%. Badania doświadczalne wykazały 8% obniżenie drgań oscylatora. W przypadku badań doświadczalnych układu ze sprężyną SMA, wyniki w pewnym stopniu odbiegają od numerycznych (rys. 13 i rys, 14). Prawdopodobnie wynika to z przyjętego modelu oraz z problemu z utrzymaniem stałej i równej temperatury w całej sprężyme.

87