8254445125

54

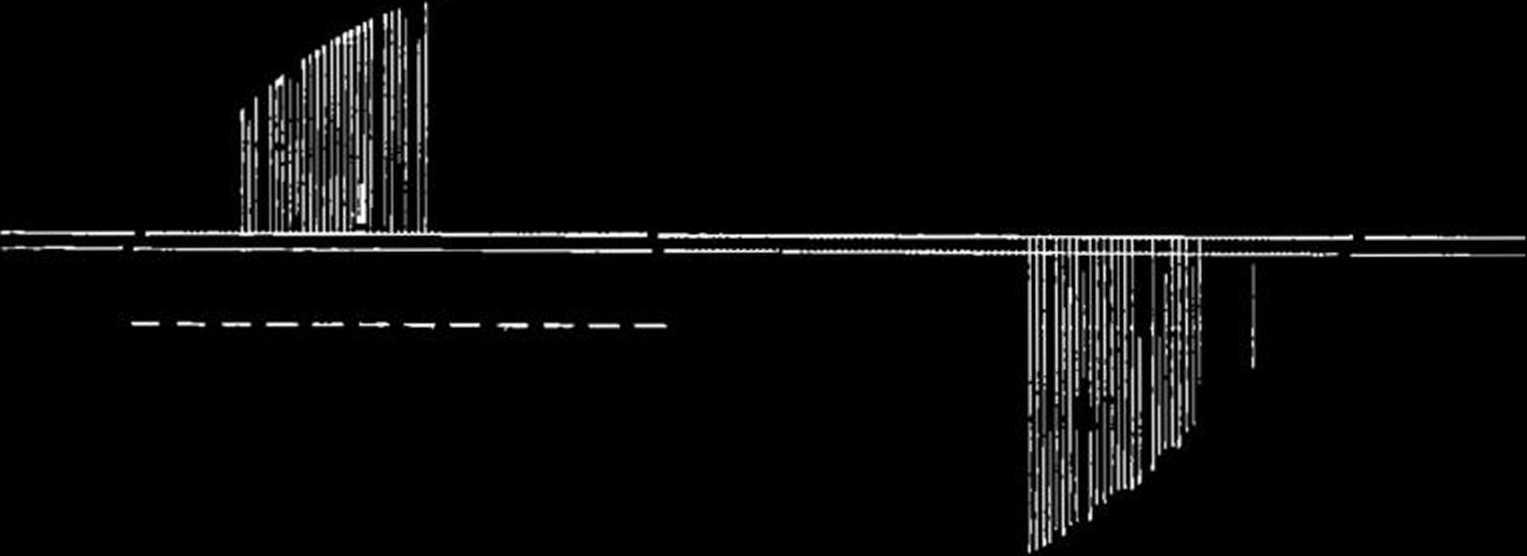
Ponieważ Am<mB, więc i CncnD (trapezy uważamy za prostokąty, gdyż Ah jest b. małe). Przez obniżenie linji rozdzielczej AB do pozycji CD rezultat będzie taki, że powierzchnia pierwszego segmentu wzrośnie o powierzchnię A h.Cn, zaś drugiego zmniejszy się o powierz-

s

T

Rys. 42.

chnięA h.nD, lecz więcej powierzchni ubędzie niż przybędzie, a w ogólnym wyniku ubędzie A h(mD—Cn). Opuszczając powtórnie linję rozdzielczą CD wdół o wysokość jh w konsekwencji dla obu segmentów razem, znów zyskujemy zmniejszenie ogólnej powierzchni o pewną wielkość, lecz nieco mniejszą od Ah(nD—Cn), ponieważ odcinek Cn ku dołowi stopniowo się zwiększa, zaś odcinek nD stopniowo się zmniejsza. Powtarzając tę operację w dalszym ciągu, dojdziemy wreszcie do takiego stanu, że podstawy prostokątów w obu segmentach zrównają się, a wtedy o ile się zwiększy powierzchnia pierwszego segmentu, o tyle się zmniejszy powierzchnia drugiego segmentu, a zatem dalsze opuszczenie linji rozdzielczej spowodowałoby zjawisko odwrotne, t. j., że powierzchnia dodawanego wąskiego paska prostokąta w pierwszym segmencie zaczęłaby wzrastać, a w drugim segmencie — zaczęłaby się zmniejszać. Stąd wnioskujemy, że dla osiągnięcia minimum momentów transportów opuszczanie linji rozdzielczej AB winno się odbywać poty, póki zrównają się podstawy segmentów, t. j. póki PR zrówna się z RQ. Zatem PQ będzie poszukiwaną linją rozdzielczą, zapewniającą minimalną sumę powierzchni segmentów, tern samem, minimalną sumę momentów transportów, a w swej dalszej konsekwencji — najekonomiczniejsze wykonanie robót ziemnych transportowych.

Powyższe dowodzenie odnosi się również do dowolnej ilości segmentów, o czem przekonamy się poniżej. Przyjmując (rys. 43) za linję rozdzielczą odcinek PQ, widzimy z grafiku krzywej Brucknera, że suma cię-