8857686414

2.3 Układy ciągłe: rachunek różniczkowy i całkowy ułamo-wego rzędu

W podrozdziale tym zostaną przedstawione podstawowe definicje różniczko-całek ułamkowego rzędu, wraz z przykładami. Definicje te unifikują definicje różniczki i całki w jedną definicję różniczko-całki. Dla rzędu dodatniego (a > 0) otrzymujemy pochodną, dla rzędu ujemnego (a < 0) otrzymujemy całkę, a dla a — 0 tę samą funkcję. Na początku zostanie przedstawiona definicja Riemanna-Liouville’a (w skrócie R-L), która jest rozszerzeniem reguły Cauchy’ego całkowania wielokrotnego. Następnie pokazana zostanie definicja Caputo, będąca modyfikacją definicji R-L, po czym zostanie przedstawiona definicja Griinwalda-Letnikowa (w skrócie G-L), która jest rozszerzeniem definicji pochodnej wielokrotnej całkowitego rzędu. Zostaną także podane podstawowe właściwości tych definicji. Na szczególną uwagę zasługuje fakt, przedstawiony w książce [162], jednoznaczności definicji R-L i G-L (przy założeniu odpowiedniej klasy różniczkowalności funkcji). Jest to wyrazem unifikacji, jaką daje rachunek różniczkowy ułamkowego rzędu. Rozpoczynając uogólnianie od definicji całki czy od pochodnej otrzymujemy jednoznaczne definicje różniczko-całki ułamkowego rzędu.

W rozdziale tym zostanie przedstawiony także transmitancja ułamkowego rzędu wraz z przykładami charakterystyk Bode’go podstawowych członów dynamicznych ułamkowego rzędu, po czym przedstawiony zostanie układ ciągły ułamkowego rzędu opisany w przestrzeni stanu, wraz z podstawowymi własnościami.

2.3.1 Definicja Riemanna-Liouville’a

Przedstawienie definicji całki ułamkowego rzędu zostanie rozpoczęte (jak to ma miejsce w [77]) od wzoru na całkowanie wielokrotne

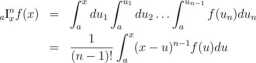
(2.4)

gdzie n G N jest krotnością całkowania, (a, x) jest przedziałem całkowania funkcji f(u). Korzystając z zależności (n — 1)! = T(n) można uogólnić wzór 2.4 na n € IŁ Otrzymujemy w ten sposób zależność Riemanna-Liouville’a na wyznaczanie całki ułamkowego rzędu.

18