1tom020

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI

W praktyce najczęściej występuje niezawodność wykładnicza P(f) = e“*. (t > 0, a > 0)

Wówczas funkcja intensywności uszkodzeń jest stała i wynosi r(t) = a.

1.2.9. Rachunek błędów. Interpolacja, aproksymacja funkcji

Błędy pomiaru dzieli się na dwie kategorie. Do błędów systematycznych zalicza się błędy, które zniekształcają wynik pomiaru, zachowując ustaloną prawidłowość. Pozostałe błędy zalicza się do kategorii błędów przypadkowych. Przyjmuje się, że błędy przypadkowe równe co do modułu są jednakowo prawdopodobne, błędy małe co do modułu są bardziej prawdopodobne niż duże oraz, że prawdopodobieństwo wystąpienia błędu przekraczającego co do modułu liczbę E, zwaną granicą możliwych błędów, jest praktycznie równe zeru.

Jeżeli przyjmuje się, że błąd a jest zmienną losową ciągłą, to dystrybuanta F(«) rozkładu błędów jest równa F(s) = P(a < «), czyli prawdopodobieństwu tego, że błąd a nie przekroczy wartości e. Prawdopodobieństwo tego, że błąd a będzie się znajdował w z góry ustalonych granicach jest równe całce

fr

P (a < a < b) = f <p(e) de

a

gdzie <p(e) jest funkcją gęstości rozkładu błędów (patrz p. 1.2.8).

Błędy przypadkowe mogą mieć różne rozkłady. Jeżeli jednak przyjmuje się założenie, że najbardziej prawdopodobną wartością szukanej wielkości jest średnia arytmetyczna wyników pomiarów (postulat Gaussa), to rozkład błędów jest rozkładem normalnym. Tym samym funkcja gęstości rozkładu błędów ma postać

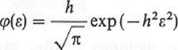
gdzie h — miara dokładności.

Porównując funkcję gęstości rozkładu normalnego (patrz tabl. 1.8) z funkcją gęstości rozkładu błędów można stwierdzić, że miara dokładności h jest związana z wariancją o relacją

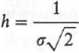
Wzór ten jest często wykorzystywany przy obliczeniach. Jeżeli wynikiem pomiarów pewnej wielkości A, wykonanych z jednakową dokładnością, są liczby x_t,i = 1,2,... n, to najbardziej prawdopodobną wartością miary dokładności jest

l

h =

gdzie x — wartość średnia

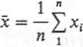
Natomiast, jeżeli pomiary są niejednakowo dokładne i doprowadziły do wyników Xj,i = 1,2,...,n, z miarami dokładności odpowiednio h_t, i = 1,2to wprowadzając liczby g_f, i = 1,2— zwane wagami pomiarów — spełniające warunek

hf = g_th², i = 1,2,..„»

otrzymuje się

n

J

gdzie x =

i

n

Y.9i

Problem błędów przy obliczeniach wykonywanych na maszynach cyfrowych jest omówiony szczegółowo w [1.2].

' W celu matematycznego opracowania wyników doświadczeń można posłużyć się interpolacją lub aproksymacją funkcji.

Interpolacja

Zagadnienie interpolacji funkcjif(x) polega na znalezieniu funkcji F(x), która w (n +1) punktach x₀,x_l,...,x„ danego przedziału <a,b), w którym jest określona funkcja f(x), przyjmuje wartości funkcjif(x) oraz przybliża wartości tej funkcji w punktach pośrednich, wraz z oszacowaniem błędów interpolacji.

Funkcję F(x)nazywa sięfunkcją interpolacyjną, zaś punkty x_i,i = 0,1,2.....n, należące do

przedziału <a,h>, nazywa się węzłami. Funkcję interpolacyjną F(x) poszukuje się najczęściej w postaci wielomianów algebraicznych lub trygonometrycznych Fouriera. Dobre wyniki daje interpolacja wielomianem Lagrange'a

gdzie: a„(x) = (x-x₀)(x-x_])...(x-x„), zaś co„(x_i) jest wartością pochodnej wielomianu co„(x) w punkcie x_y Można wykazać, że błąd interpolacji w tym przypadku wynosi

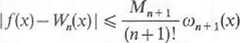
gdzie M„₊₁= sup |/<"^+1,(x)

Aproksymacja

Aproksymacja lub przybliżenie danej funkcji F(x) polega na wyznaczeniu parametrów «j,i=l,....m funkcji y = f(x,a_y,...,aj przybliżającej wartości zadanej funkcji F(x) w punktach F(Xj) = y„i = l,...,n. Funkcja F(x) może być określona wzorem lub tablicą wartości.

Najbardziej rozpowszechnioną metodą aproksymacji jest metoda najmniejszych kwadratów, zwana często metodą średniokwadratową. Metoda ta polega na doborze parametrów a_hi = 1 w taki sposób, aby zminimalizować wyrażenie

n

1

Najczęściej jako funkcję aproksymującą przyjmuje się funkcję

n

f(x) = XUi<P,(A)