Rodzaje sił:1.skupione;2.powierzchniowe

1.zewnetrzne(aktywne;reakcji) 2.wewnetrzne

Wiezy przykłady: przegub walcowy, kulisty,podpora przegubowa stala i przesuwna,ciegna

Warunki rownowagi:

Układy sil na plaszczyznie

A.ukłąd sil zbieznych(wszystkie kierunki sil musza zbiegac si w jaednym punkcie)

r. rownowagi dla sil zbieznych na plaszczyznie:

b)uklad sil rownoleglych. Rownania rownowagi:
(lub zamiast y i 0 wstawic A i B)

Tarcie i praca tarcia:

Prawa Coulomba i Morena:

1.sila tarcia jest niezalezna od wielkosci stykajacych się ze soba powierzcchni i zalezy jedynie od ich rodzaju.

2.Wielkosc sily tarcia dalc iala znajdujacego się w spoczynku może się zmieniac od zera do maksymalnej wartsci proporcjonalnej do calkowitego nacisku normalnego

3.W przypadku gdy cialo slizga się po pewnej powierzchni, sila tarcia jest skierowana zawsze przeciwnie do kierunku ruchu.

Wniosek t<=μN

Dynamika:

Bezwladnosciowy uklad odniesienia- uklad w którym obowiazuja 3 prawa Newtona.

Zasada wzglednosci mechaniki klasycznej-uklad odniesienia poruszajacy się względem ukladu bezwladnosciowego ruchem jednostajnym prostoliniowym tez jest ukl. Bezwladnosciowym.

Ruch prostolinowy nieswobodny-przykład rownia pochyla

Rcu krzywoliniowy nieswobodny-punkt o masie m , na który dziala sila p może poruszac się tylko po lini l. Na punkt działa siła reakcji więzów R. Rownanie dynamiczne mp=P+R

Naturalny ukłąd wspolrzednych:τ-styczna,β-binormalna,υ-normalna

Wszystko rzutujemy na 3 osie naturalnego ukl.( τ,β,υ)

Rownania dynamiczne ruchu:

Jeśli pojawi się tarcie to:

Sila N jest rowna reakcji wiezow prostopadlych do linii l. Przykład wahadlo mat.

Ruch pod wplywem sily centralnej(linia dzilania sily przechodzi stale przez nieruchomy punkt O(sreodek sily))

P_r=-P(r), P_φ=0

M(r''-rφ'²)=-P(r), m/r*d(r²φ')/dt=0

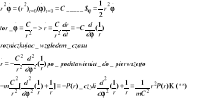
Prawo ciazenia powszechnego

Podstawiaja do (**)
i u=1/r otrzymujemy:

wstawiamy:

rozwiazujemy rownanie i wychodzi:

(☼)

Ruch pod wplywem ciazenia ziemskiego:

=mg κM=R²g->P=mgR²/r²

(□)

->C=r₀v₀

Rozwiazujemy rowanie rozniczkowe(□)

φ₀=0,r|_φ=0=r₀;dr/dφ=0->

w rownaniu(☼)
e<1-elipsa;e=0-okrag;e>1-hiperbola,e=1-parabola

---