Egzamin z rachunku prawdopodobieństwa
17 czerwca 1999
Imię i Nazwisko............................................................................Nr indeksu.............
1. Z przedziału <−1,1> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .
2. Doświadczenie polegające na rzucie trzema monetami powtarzamy tak długo, dopóki nie otrzymamy trzech orłów jednocześnie. Niech X oznacza liczbę wykonanych doświadczeń. Obliczyć:
a) ,
b) EX.
3. Dwuwymiarowa zmienna losowa ma rozkład o funkcji gęstości
gdzie D jest trójkątem o wierzchołkach (0,0), (1,0), (1,1).
a) Wyznaczyć stałą c.
b) Wyznaczyć rozkłady brzegowe zmiennych .
c) Zbadać niezależność zmiennych .
4. Jednowymiarowa zmienna losowa X ma rozkład dla k = 1,2,...
a) Wyznaczyć stałą a.
b) Wyznaczyć funkcję charakterystyczną zmiennej losowej X.
c) Wyznaczyć funkcję charakterystyczną zmiennej losowej Y = X − 1.
5. Niezależne zmienne losowe mają jednakowy rozkład o funkcji charakterystycznej . Obliczyć przybliżoną wartość prawdopodobieństwa .
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
Imię i Nazwisko......................................................................................
1. Obliczyć prawdopodobieństwo zdarzenia, że pierwiastki równania ax2 + bx + 1 = 0 są rzeczywiste, jeśli liczby a i b zostały wybrane losowo z przedziału <−1,1>.
2. Rzucamy dwukrotnie kostką sześcienną. Niech A oznacza zdarzenie : wśród wyrzuconej liczby oczek jest co najmniej jedna szóstka, B - zdarzenie: wśród wyrzuconej liczby oczek jest co najwyżej jedna liczba parzysta. Zbadać, czy zdarzenia A i B są niezależne.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) wyznaczyć stałą c,
b) wyznaczyć dystrybuantę zmiennej X,
c) wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej Y = X2 −1.
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład o stałej gęstości na trójkącie o wierzchołkach (0,0), (0,2), (2,0). Obliczyć współczynnik korelacji zmiennych X1, X2.
5. Wyznaczyć funkcję charakterystyczną zmiennej losowej X i Y = 4 − 2X, gdzie X ma rozkład określony tabelką
.
a) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład Bernoulliego z parametrami
n, dla n=1,2,...,
będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie
Yn = n−3Xn − 3n,
spełnia słabe i mocne prawo wielkich liczb.
egzamin z rachunku prawdopodobieństwa
drugi termin
luty 1998
Imię i Nazwisko.........................................................................................................
1. 1800 razy wybieramy losowo jeden punkt z przedziału <1,5>. Obliczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że 550 razy otrzymamy punkt, którego odległość od środka przedziału <1,5> jest większa od 1/3 długości tego przedziału.
2. Zmienna losowa X ma rozkład bezwzględnie ciągły o funkcji gęstości
a) Wyznaczyć stałą c.
b) Wyznaczyć dystrybuantę zmiennej X.
c) Wyznaczyć funkcję gęstości zmiennej .
3. Dwuwymiarowa zmienna losowa ma rozkład czysto skokowy o funkcji prawdopodobieństwa , gdzie N = {1,2,...}, określonej wzorem
.
a) Wyznaczyć stałą c.
b) Zbadać niezależność zmiennych X1, X2.
c) Obliczyć prawdopodobieństwo zdarzenia, że .
4. Niezależne zmienne losowe mają identyczny rozkład gamma z parametrami . Wyznaczyć funkcję charakterystyczną zmiennej
.
Sprawdzić, czy funkcja charakterystyczna zmiennej Y przyjmuje tylko wartości rzeczywiste. Odpowiedż uzasadnić.
5. Niech będzie ciągiem takich niezależnych zmiennych losowych, że zmienna Xn (n=1,2,...) ma rozkład o funkcji gęstości
Sprawdzić, czy ciąg spełnia słabe i mocne prawo wielkich liczb.
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
Imię i Nazwisko......................................................................................
1. Obliczyć prawdopodobieństwo zdarzenia, że pierwiastki równania są rzeczywiste, jeśli liczby b i c zostały wybrane losowo z przedziału <−1,1>.
2. Rzucamy dwukrotnie kostką sześcienną. Niech A oznacza zdarzenie : wśród wyrzuconej liczby oczek jest co najmniej jedna czwórka, B - zdarzenie: wśród wyrzuconej liczby oczek jest co najwyżej jedna liczba nieparzysta. Zbadać, czy zdarzenia A i B są niezależne.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) wyznaczyć stałą c,
b) wyznaczyć dystrybuantę zmiennej X,
c) wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej .
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład normalny o funkcji gęstości
.
Wyznaczyć rozkład zmiennej
5. Zmienna losowa X ma rozkład określony tabelką
.
a) Wyznaczyć funkcję charakterystyczną zmiennej losowej X i Y = 4 − 2X.
b) Czy funkcja charakterystyczna zmiennej losowej X przyjmuje tylko wartości rzeczywiste? Odpowiedź uzasadnić.
c) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład o funkcji charakterystycznej dla
n 1,2,..., będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie Yn = n−2Xn cos(n), spełnia słabe i mocne prawo wielkich liczb.
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
Imię i Nazwisko......................................................................................
1. Z przedziału <-2,2> wybrano losowo dwie liczby x i y. Obliczyć prawdopodobieństwo zdarzenia, że xy ≤ 1.
2. Z urny zawierającej 1 kulę białą i 99 czarnych losujemy ze zwracaniem 80 razy po jednej kuli. Obliczyć przybliżoną wartość prawdopodobieństwa wylosowania co najwyżej dwa razy kuli białej.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) wyznaczyć stałą c,
b) wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej Y = X2 −1.
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład o stałej gęstości na trójkącie o wierzchołkach (0,0), (1,1), (1,0). Obliczyć współczynnik korelacji zmiennych X1, X2.
5. Wyznaczyć funkcję charakterystyczną zmiennej losowej Y = X1 − X2, gdzie X1, X2
są niezależnymi zmiennymi losowymi o jednakowym rozkładzie określonym tabelką
.
a) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład N(n,1) dla n=1,2,..., będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie Yn = n−1Xn + n, spełnia słabe i mocne prawo wielkich liczb.
Egzamin z rachunku prawdopdobieństwa
styczeń 1998
Imię i Nazwisko..................................................................................................
1. Wybieramy losowo dwie liczby a i b z przedziału <1,1>. Obliczyć prawdopodobieństwo zdarzenia, że .
2. Ze zbioru liczb 1,2,...,200 losujemy 10000 razy ze zwracaniem po jednej liczbie. Wyznaczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że liczb parzystych otrzymamy co najmniej o dwieście więcej niż nieparzystych.
3. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX.
c) Wyznaczyć rozkład zmiennej Y X2.
d) Obliczyć EY.
4. Dwuwymiarowa zmienna losowa X (X1,X2) ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Wyznaczyć dystrybuantę zmiennej X.
5. Zmienna losowa X ma rozkład określony tabelką
.
a) Wyznaczyć funkcję charakterystyczną zmiennej losowej X i Y 3 − X.
b) Wykazać, że funkcja charakterystyczna zmiennej losowej X przyjmuje tylko wartości rzeczywiste.
c) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn (n 1,2,...) ma rozkład o funkcji charakterystycznej , będzie ciągiem niezależnych zmiennych losowych. Dla jakich a∈R ciąg (Yn), gdzie, spełnia warunek Kołmogorowa.
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
Imię i Nazwisko......................................................................................
1. Z przedziału <-2,2> wybrano losowo dwie liczby x i y. Obliczyć prawdopodobieństwo zdarzenia, że xy ≤ 2.
2. Z urny zawierającej 1 kulę białą i 99 czarnych losujemy ze zwracaniem 80 razy po jednej kuli. Obliczyć przybliżoną wartość prawdopodobieństwa wylosowania co najwyżej dwa razy kuli białej.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) wyznaczyć stałą c,
b) wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej Y = X2 −1.
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład o stałej gęstości na trójkącie o wierzchołkach (0,0), (1,1), (1,0). Obliczyć współczynnik korelacji zmiennych X1, X2.
5. Wyznaczyć funkcję charakterystyczną zmiennej losowej Y = X1 − X2, gdzie X1, X2
są niezależnymi zmiennymi losowymi o jednakowym rozkładzie określonym tabelką
.
a) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład N(n,1) dla n=1,2,..., będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie Yn = n−1Xn + n, spełnia słabe i mocne prawo wielkich liczb.
Egzamin Extra z rachunku prawdopdobieństwa
Imię i Nazwisko..................................................................................................
1. Wybieramy losowo dwie liczby a i b z przedziału <1,1>. Obliczyć prawdopodobieństwo zdarzenia, że .
2. Ze zbioru liczb 1,2,...,200 losujemy 10000 razy ze zwracaniem po jednej liczbie. Wyznaczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że liczb parzystych otrzymamy o dwieście więcej niż nieparzystych.
3. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX i D2X.
c) Wyznaczyć rozkład zmiennej Y = X2.
d) Obliczyć EY.
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład normalny o funkcji gęstości
.
Wyznaczyć rozkład zmiennej
5. Zmienna losowa X ma rozkład określony tabelką
.
a) Wyznaczyć funkcję charakterystyczną zmiennej losowej X i Y = 4 − 2X.
b) Czy funkcja charakterystyczna zmiennej losowej X przyjmuje tylko wartości rzeczywiste? Odpowiedź uzasadnić.
c) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład o funkcji charakterystycznej dla
n 1,2,..., będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie Yn = n−2Xn cos(n), spełnia słabe i mocne prawo wielkich liczb.
Egzamin poprawkowy z rachunku prawdopodobieństwa
Imię i Nazwisko........................................................................................................
1. Z przedziału (2,2) wybieramy losowo dwie liczby x i y. Obliczyć prawdopodobieństwo zdarzenia, że .
2. Obliczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że w 180 rzutach kostką otrzymamy 3 oczka co najmniej 40 razy.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gestości
a) Wyznaczyć stałą c.
b) Wyznaczyć dystrybuantę zmiennej X.
c) Sprawdzić, czy istnieją momenty , gdzie k∈N, zmiennej X.
4. Dwuwymiarowa zmienna losowa ma rozkład jednostajny w prostokącie 0,1>x0,π>. Wyznaczyć rozkład zmiennej , gdzie , .
5. Funkcja charakterystyczna jednowymiarowej zmiennej losowej X określona jest wzorem
.
a) Wyznaczyć rozkład zmiennej X.
b) Wyznaczyć funkcję charakterystyczną zmiennej .
6. Niech będzie ciągiem niezależnych zmiennych losowych o rozkladach normalnych N(1,n). Sprawdzić, czy ciąg , gdzie , spełnia słabe i mocne prawo wielkich liczb.
Egzamin z rachunku prawdopodobieństwa
28 stycznia 2000
Imię i Nazwisko.............................................................................Nr indeksu...............
1. Z przedziału <−1,1> wybieramy losowo dwa punkty x i y. Wyznaczyć w zależności od wartości parametru a ∈ R prawdopodobieństwo zdarzenia .
2. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Wyznaczyć dystrybuantę zmiennej X.
c) Obliczyć EX i .
3. Niezależne zmienne losowe , mają rozkłady o funkcjach charakterystycznych odpowiednio równych , .
a) Wyznaczyć tabelkę rozkładu prawdopodobieństwa dwuwymiarowej zmiennej losowej .
b) Wyznaczyć dystrybuantę rozkładu prawdopodobieństwa dwuwymiarowej zmiennej losowej .
c) Obliczyć współczynnik korelacji , gdzie , .
4. Niech będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach określonych tabelką
.
Obliczyć przybliżoną wartość prawdopodobieństwa .
5. Niech będzie wstępującym (tzn. dla n ∈ N) ciągiem zdarzeń losowych takich, że
, dla n ∈ N.
Obliczyć 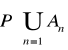
.
Egzamin z rachunku prawdopodobieństwa
28 stycznia 2000
Imię i Nazwisko.............................................................................Nr indeksu...............
1. Z przedziału <−1,1> wybieramy losowo dwa punkty x i y. Wyznaczyć w zależności od wartości parametru a ∈ R prawdopodobieństwo zdarzenia .
2. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Wyznaczyć dystrybuantę zmiennej X.
c) Obliczyć EX i .
3. Niezależne zmienne losowe , mają rozkłady o funkcjach charakterystycznych odpowiednio równych , .
a) Wyznaczyć tabelkę rozkładu prawdopodobieństwa dwuwymiarowej zmiennej losowej .
b) Wyznaczyć dystrybuantę rozkładu prawdopodobieństwa dwuwymiarowej zmiennej losowej .
c) Obliczyć współczynnik korelacji , gdzie , .
4. Niech będzie ciągiem niezależnych zmiennych losowych o jednakowych rozkładach określonych tabelką
.
Obliczyć przybliżoną wartość prawdopodobieństwa .
5. Niech będzie zstępującym (tzn. dla n ∈ N) ciągiem zdarzeń losowych takich, że
, dla n ∈ N.
Obliczyć 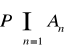
.
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
sem. zimowy 96/97
Imię i Nazwisko......................................................................................
1. Z przedziału <-1,1> wybrano losowo dwie liczby a i b. Obliczyć prawdopodobieństwo zdarzenia, że trójmian kwadratowy nie ma rzeczywistych pierwiastków.
2. Z urny zawierającej 1 kulę białą i 99 czarnych losujemy ze zwracaniem 80 razy po jednej kuli. Obliczyć przybliżoną wartość prawdopodobieństwa wylosowania co najwyżej dwa razy kuli białej.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) wyznaczyć stałą c,
b) wyznaczyć dystrybuantę zmiennej X,
c) wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej Y = X2 −1.
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład o stałej gęstości na trójkącie o wierzchołkach (0,0), (1,1), (1,0). Obliczyć współczynnik korelacji zmiennych X1, X2.
5. Wyznaczyć funkcję charakterystyczną zmiennej losowej Y = 2X1 − X2, gdzie X1, X2
są niezależnymi zmiennymi losowymi o jednakowym rozkładzie określonym tabelką
.
a) Obliczyć EY, D2Y.
6. Niech (Xn), gdzie Xn ma rozkład o funkcji charakterystycznej dla n = 1,2,..., będzie ciągiem niezależnych zmiennych losowych. Sprawdzić, czy ciąg (Yn), gdzie Yn = n−3/2 (Xn + 1), spełnia słabe i mocne prawo wielkich liczb.
EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
sem. letni 96/97
Imię i Nazwisko......................................................................................
1. Z przedziału <-2,2> wybrano losowo dwie liczby b i c. Obliczyć prawdopodobieństwo zdarzenia, że trójmian kwadratowy ma rzeczywiste pierwiastki.
2. Z urny zawierającej 1 kulę białą i 99 czarnych losujemy ze zwracaniem 100 razy po dwie kule. Obliczyć przybliżoną wartość prawdopodobieństwa wylosowania co najwyżej dwa razy pary kul o różnych kolorach.
3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c,
b) Wyznaczyć dystrybuantę zmiennej X,
c) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej .
4. Dwuwymiarowa zmienna losowa X = (X1,X2) ma rozkład o stałej gęstości na trójkącie o wierzchołkach (0,0), (1,1), (1,1). Obliczyć współczynnik korelacji zmiennych X1, X2.
5. Niezależne zmienne losowe X1,X2 mają rozkłady gamma odpowiednio z parametrami λ1 = λ2 oraz s1 = 3s2. Wyznaczyć wartości tych parametrów, jeśli zmienna ma rozkład χ2 o sześciu stopniach swobody.
6. Niech X1,...,X200 będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie o funkcji charakterystycznej . Obliczyć przybliżoną wartość prawdopodobieństwa .
Egzamin Extra z rachunku prawdopdobieństwa
Imię i Nazwisko..................................................................................................
1. Wybieramy losowo dwie liczby a i b z przedziału <-1,1>. Obliczyć prawdopodobieństwo zdarzenia, że .
2. Ze zbioru liczb 1,2,...,200 losujemy 10000 razy ze zwracaniem po jednej liczbie. Wyznaczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że otrzymamy nie mniej liczb parzystych niż nieparzystych.
3. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX i D2X.
c) Wyznaczyć rozkład zmiennej Y = X2.
d) Obliczyć EY.
4. Rzucamy dwukrotnie kostką sześcienną. Niech zmienna X1 oznacza sumę liczb wyrzuconych oczek, a X2 będzie zmienną taką, że
a) Wyznaczyć rozkład dwuwymiarowej zmiennej losowej .
b) Wyznaczyć rozkłady brzegowe.
c) Zbadać niezależność zmiennych X1 i X2.
Egzamin z rachunku prawdopodobieństwa
10 czerwca 1998
Imię i Nazwisko......................................................................grupa............................
1. Z przedziału <0,2> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .
2. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX i D2X.
c) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej .
3. Niech będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie. Wyznaczyć rozkład zmiennej , jeśli wiadomo, że zmienna ma dystrybuantę określoną wzorem
4. Dwuwymiarowa zmienna losowa ma funkcję gęstości określoną wzorem
gdzie D jest trójkątem o wierzchołkach w punktach (0,0), (1,0), (0,−1).
a) Wyznaczyć stałą c.
b) Wyznaczyć macierz kowariancji zmiennych .
5. Dwuwymiarowa zmienna losowa ma rozkład określony tabelką
.
a) Zbadać niezależność zmiennych .
b) Wyznaczyć funkcję charakterystyczną zmiennej .
c) Czy funkcja charakterystyczna zmiennej Y przyjmuje tylko wartości rzeczywiste.
6. Niech będzie ciągiem takich niezależnych zmiennych losowych, że zmienna (n∈N) ma funkcję charakterystyczną . Dla jakich a ∈ R ciąg spełnia warunek Kołmogorowa.
Egzamin z rachunku prawdopodobieństwa
10 czerwca 1998
Imię i Nazwisko......................................................................grupa............................
1. Z przedziału <0,1> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .
2. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX i D2X.
c) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej .
3. Niech będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie. Wyznaczyć rozkład zmiennej , jeśli wiadomo, że zmienna ma dystrybuantę określoną wzorem
4. Dwuwymiarowa zmienna losowa ma funkcję gęstości określoną wzorem
gdzie D jest trójkątem o wierzchołkach w punktach (0,0), (−1,0), (0,1).
a) Wyznaczyć stałą c.
b) Wyznaczyć macierz kowariancji zmiennych .
5. Dwuwymiarowa zmienna losowa ma rozkład określony tabelką
.
a) Zbadać niezależność zmiennych .
b) Wyznaczyć funkcję charakterystyczną zmiennej .
c) Czy funkcja charakterystyczna zmiennej Y przyjmuje tylko wartości rzeczywiste.
6. Niech będzie ciągiem takich niezależnych zmiennych losowych, że zmienna (n∈N) ma funkcję charakterystyczną . Dla jakich a ∈ R ciąg spełnia warunek Kołmogorowa.
Egzamin z rachunku prawdopodobieństwa
wrzesień 1998
Imię i Nazwisko......................................................................grupa............................
1. Z przedziału <0,1> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .
2. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć stałą c.
b) Obliczyć EX i D2X.
c) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej .
3. Niech będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie wykładniczym z parametrem λ. Wyznaczyć dystrybuantę zmiennej .
4. Dwuwymiarowa zmienna losowa ma funkcję gęstości określoną wzorem
gdzie D jest trójkątem o wierzchołkach w punktach (0,0), (1,0), (0,1).
a) Wyznaczyć stałą c.
b) Wyznaczyć macierz kowariancji zmiennych .
5. Dwuwymiarowa zmienna losowa ma rozkład określony tabelką
.
a) Wyznaczyć p.
b) Wyznaczyć rozkład zmiennej .
c) Wyznaczyć funkcję charakterystyczną zmiennej .
6. Niech będzie ciągiem takich niezależnych zmiennych losowych, że zmienna (n∈N) ma funkcję charakterystyczną . Dla jakich a ∈ R ciąg spełnia warunek Kołmogorowa.
Egzamin z rachunku prawdopodobieństwa
(extra)
Imię i Nazwisko.................................................................................gr.......................
1. Wybieramy losowo punkt (x,y) z trójkąta o wierzchołkach (0,0), (1,0), (0,1). Dla jakiej wartości parametru a ∈ R prawdopodobieństwo zdarzenia, że y ≤ ax jest równe 1/2 ?
2. Zmienna losowa X ma rozkład o funkcji gęstości
a) Wyznaczyć wartość parametru a.
b) Obliczyć EX i D2X.
c) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej Y ln X.
Wyszukiwarka
Podobne podstrony:
rachunek pra, kol2, KOLOKWIUM II Z RACHUNKU PRAWDOPODOBIEŃSTWA
zagadnienia teoretyczne na egzamin, dokumenty, polibuda, sem 2, rachunek prawdopodobienstwa
Pytania egzaminacyjne z rachunku prawdopodobieństwa i statystyki, Pytania egzaminacyjne
rachunek pra, kol1r, KOLOKWIUM I Z RACHUNKU PRAWDOPODOBIEŃSTWA
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Matematyka - rachunek prawdopodbieństwa - ściąga, szkoła
09 Rachunek prawdopodobie ästwaid 7992
7 ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA
MATEMATYKA Rachunek prawdopodobieństwa, str tytułowa, Marcin Nowicki
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka dzienne wyklad1, Rachunek prawdopodobie˙stwa
1 zadania z rachunku prawdopodobieństwa, Zad
Zestaw10 rachunek prawdopodobie Nieznany
więcej podobnych podstron