AUTOMAT

skończony ⇔ nieskończony

zupełny ⇔ niezupełny

deterministyczny ⇔ probabilistyczny

Automat - układ sekwencyjny - posiada choćby jedną pętlę sprzężenia zwrotnego.

i
to czysto kombinacyjna część automatu;
to część pamięciowa.

Układy bez pętli sprzężenia zwrotnego są zawsze kombinacyjnymi, ale na odwrót

s być nie musi. Przykład:

x	y	z
0	0	0
1	1	1

Poniżej wyjścia : y, z, s nie są zdefiniowane dla każdej kombinacji wejść x.

x	y	z	s
0	1	0	1
1	×	×	×

Automaty MOORE'a i MEALY'ego

Automat to uporządkowana struktura - wszystkie zbiory skończone i niepuste.

- zbiór sygnałów wejściowych (alfabet);

- zbiór stanów wewnętrznych (alfabet);

- zbiór sygnałów wyjściowych (alfabet);

- funkcja przejść;

- funkcja wyjść;

- dziedzina funkcji przejść;

MEALY
MOORE - dziedziny funkcji wyjść;

Gdy znak
zastąpiony przez =, to automat jest zupełny
i
określone dla wszystkich par
.

Przykład:

STANY \ WEJŚCIA	LOLO	BOLO	LOLO	BOLO
ALA	OLA	OLA	PIES	-
OLA	-	ELA	KOT	-
ELA	-	ALA	PIES	-
	tabela przejść		tabela wyjść

GRAF STANÓW

Równoważność automatów

Automaty generują te same ciągi wyjściowe w odpowiedzi na ciągi wejściowe.

Automat A jest równoważny automatowi B
jeżeli
i dla każdego
automaty te generują identyczne
. Ustalona relacja równoważności w klasie automatów skończonych.

Dwa stany
oraz
automatu A są równoważne jeżeli automat rozpoczynający pracę w stanie
jest równoważny automatowi A rozpoczynającemu pracę w
.

Jeżeli dwa stany są równoważne to jeden z nich jest nadmiarowy.

Twierdzenie. A jest automatem MOORE'a lub MEALY'ego.

Stany
oraz
są równoważne ⇔

1. 
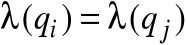
   MOORE

MEALY

b)
.

LOLO / KOT

BOLO / -

BOLO / -

LOLO / PIES

BOLO / -

ELA

OLA

ALA

---