Wykład 7
Metody pomiarowe
Pomiar metodą bezpośredniego porównania z wzorcem
Zasada cyfrowego pomiaru czasu i częstotliwości
(metoda -greckie methodos = badanie;
-w nauce sposób badania rzeczy i zjawisk, ogół reguł stosowany przy badaniu rzeczywistości,
-powszechnie świadomie i konsekwentnie stosowany sposób dla osiągnięcia określonego celu.)
Podziału metod pomiarowych można dokonać wedługróżnych kryteriów np.:
rodzaju wielkości fizycznych mierzonych za ich pomocą (metody optyczne, elektryczne, cieplne..,)
rodzaju wielkości fizycznych mierzonych za ich pomocą (metody optyczne, elektryczne, cieplne..,)
sposobu przekazywania informacji obserwatorowi (analogowe, cyfrowe)
sposobu uzyskiwania wyniku pomiaru (bezpośrednie,pośrednie)
sposobu porównania z wzorcem (bezpośredniego, pośredniego porównania z wzorcem)
Metodologicznie najważniejszy podział na sposób porównania z wzorcem:
Pomiar metodą bezpośredniego porównania z wzorcem
Pomiar metodą pośredniego porównania z wzorcem
POMIAR METODĄ BEZPOŚREDNIEGO PORÓWNANIA Z WZORCEM ( wzorzec Ww i wielkość mierzona Wx jednorodne)
Porównanie - określenie relacji między szukaną wartością wielkości mierzonej Wx, a wartością wzorca Ww.
Wx < Ww
Wx = Ww
Wx > Ww
Istotna relacja równości, aby ją stwierdzić trzeba dysponować wzorcem i układem porównania - komparatorem.
Komparacja- łacińskie comparatio - porównanie , przyrównanie
Przykłady:
pomiar długości z użyciem wzorca długości ,
pomiar odcinka czasu,
ważenie na wadze równoramiennej.
pomiar napięcia metodą kompensacyjną.
Pomiar długości -WZORZEC długości - wyskalowana linijka
Układ porównania- przyłożenie miary wzorca do badanego obiektu, obserwator stwierdza stan zrównania lx=lw.
Co będzie decydowało o niepewności wyniku?
Δlx=Δlw+Δlzrównania
Δlw- błąd wzorca
Δlzrównania = Δl=lw=rozdzielczości wzorca lub
Δl=czułości (dokładności) porównania (komparacji)
POMIAR ODCINKA CZASU Tx
Zajmować się będziemy tylko odcinkami czasu zdefiniowanymi przez czas trwania sygnału elektrycznego.
Do pomiaru niezbędny generator wzorcowy generujący sygnał o stałym okresie Tw oraz układ porównania trwania sygnałów elektrycznych Tx i Tw.
Żądamy, aby sygnały elektryczne, których czas trwania chcemy porównywać, przyjmowały dwa poziomy napięć, wysokiemu potencjałowi przypisuje się 1; niskiemu, 0 (sygnał zero-jedynkowy).
Sygnały 0,1 można porównywać za pomocą układów logicznych.
Układ tzw BRAMKI LOGICZNEJ realizuje iloczyn sygnałów wejściowych
wej1 wej2 wyjście
0 0 0
0 1 0
1 0 0
1 1 1
Jak wykorzystać w pomiarze odcinka czasu?
wej1 Tx
wyjście - zliczenie liczby impulsów (1) pojawiającychsie na wejściu 2, gdy na wejściu 1 sygnał1 (stan wysoki)
wej2 Tw
Ile impulsów pojawi się na wyjściu bramki jeśli w czasie trwania T1 impulsu o wartości „1”; na wejściu 2 pojawi się i zniknie N-krotnie impuls T2 o wartości „1” ?
Bramka pozwala na stwierdzenie, że:
Tx=N*Tw
Jaka niepewność tak wyznaczonej wartości Tx ?
ΔTx = ΔN*Tw + N*ΔTw
Δ N=? Δ Tw=?
Δ N- błąd zrównania Δ N= ± 1
Δ Tw- błąd graniczny określenia wartości Tw
Błąd względny wyniku pomiaru Tx
δTx= δN+δTw gdzie δN = 1/N
POMIAR OKRESU I CZĘSTOTLIWOŚCI SYGNAŁÓW ELEKTRYCZNYCH
Sygnał elektryczny X(t), zmienny w czasie t, nazywamy okresowym , jeśli istnieje wartość T taka, że spełnione jest równanie X(t)=X(t+T) dla dowolnej wartości t.
Najmniejsza wartość T spełniająca ten warunek nazywa się OKRESEM, a jej odwrotność CZĘSTOTLIWOŚCIĄ.
okres 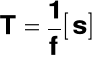
częstotliwość 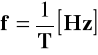
Przykład sygnału okresowego ;
sygnał sinusoidalny U(t) =Um*sinωt; ω-pulsacja; ω=2πf
Schemat blokowy okresomierza
Aby móc zmierzyć okres sygnału należy utworzyć z sygnału okresowego sygnał prostokątny (zero-jedynkowy) - potrzebny układ formujący
Co będzie decydowało o niepewności uzyskanego wyniku?
Tx=N*Tw
ΔTx=ΔN Tw +N*ΔTw
Czy czas otwarcia bramki odpowiada dokładnie wartości Tx ?
Bramka może być „otwarta” przez czas z przedziału Tx1- Tx2
Błąd wprowadzany przez układ formujący Δt zależy od parametrów układu formowania i parametrów sygnału.
Od przedziału napięcia , w którym -zamiast w momencie przejścia sygnału mierzonego przez zero -zmieni się wartość sygnału na wyjściu układu formującego.
Od szybkości narastania sygnału mierzonego
Jaki charakter ma błąd Δt układu formującgo ?
Jaki charakter mają błądy ΔN,ΔTw ?
Która składowa błędu rośnie jeśli mierzymy sygnał o coraz mniejszym okresie (większej częstotliwości)?
ZADANIE
Dobrać warunki pracy ( częstotliwość wzorcową) do pomiaru okresu sygnału prostokątnego wynoszącego około 20ms, tak aby wynik pomiaru był obarczony błędem nie większym niż 0,001%.
Generator wzorcowy umożliwia generację sygnałów o częstotliwości:1Hz, 10Hz, 100Hz, 1kHz, 10kHz, 100kHz, 1MHz, 10MHz
czyli generację sygnałów o okresie:1;0,1s; 0,01s ; 1ms; 0,1ms; 0,01ms; 1μ; 0,1μs
Błąd graniczny określenia częstotliwości wzorcowej δfw = 10-6
Rozwiązanie:
δTx=±(δTw+δN) δTw=10-6= 0,0001% (pomijalnie małe w stosunku do 0,001%)
można przyjąć , że δTx=±δN δN=1/N
czyli 1/N ma być mniejsze od 0,00001 co można uzyskać jeśli w mierzonym okresie zliczonych zostanie co najmniej 100 000 impulsów wzorcowych.
Tx=N*Tw
Tw=Tx/N
Jeśli N≥100 000 to Tw≤0,02/100 000
Stąd Tw≤0,000 000 2s; Tw≤0,2 μs
CZYLI należy wybrać częstotliwość sygnału wzorcowego o okresie 0,1μs.
Sygnały o jakim okresie można zmierzyć z błędem nie większym niż 0,01% dysponując tym generatorem wzorcowym?
Jak zmierzyć okres ( częstotliwość) sygnałów o mniejszym okresie (większej częstotliwości)
Jak zmierzyć metodą porównania odcinków czasu częstotliwość?
Schemat blokowy częstościomierza.
Czy układ formujący impuls prostokątny (former) będzie wpływał na dokładność pomiaru częstotliwości.
Dobrać warunki pracy ( częstotliwość wzorcową- czas otwarcia bramki) do pomiaru częstotliwości sygnału około 50kHz, tak aby wynik pomiaru był obarczony błędem nie większym niż 0,001%.
Generator wzorcowy umożliwia generację sygnałów o częstotliwości:0,1Hz, 1Hz, 10Hz, 100Hz, 1kHz, 10kHz, 100kHz, 1MHz, 10MHz czyli generację sygnałów o okresie:
10s; 1s; 0,1s; 0,01s ; 1ms; 0,1ms; 0,01ms; 1μ; 0,1μs
Błąd graniczny określenia częstotliwości wzorcowej δfw = 10-6
Rozwiązanie:
δfx=±(δfw+δN)
fw=10-6= 0,0001%(pomijalnie małe w stosunku do 0,001%) można przyjąć , że δfx=±δN δN=1/N
czyli 1/N ma być mniejsze od 0,00001 co można uzyskać jeśli w mierzonym okresie zliczonych zostanie co najmniej 100 000 impulsów wzorcowych.
fx=N*fw
Tw=N/fx
Jeśli N≥100 000 to Tw≤100 000/50000
Stąd
Tw≤2s; Tw=10s; fw=0,1Hz
Częstotliwość możemy mierzyć przez bezpośrednie porównanie z wzorcem bezpośrednio - wynik w Hz lub pośrednio przez pomiar okresu.
Kiedy stosować metodę bezpośrednią a kiedy pośrednią?
UWAGA
Uzupełnić materiał korzystając z podanej literatury, można także skorzystać z materiału do ćwiczenia laboratoryjnego Pomiar częstotliwości i przesunięcia fazowego -szukać na stronie WWW.kmeif.pwr.wroc.pl
Wykład 7
W4 Miernictwo elektroniczne IF 3
Wyszukiwarka
Podobne podstrony:
Pytania nr 3 (21), sem II, Podstawy Teorii Okrętów - Wykład.Laboratorium, Laboratorium nr 3 (21) - M
METODY POMIARU LĘKU, Diagnoza psychologiczna - wykłady - Maciejczyk
Opis metody pomiaru rezystancja skrośna i pow
Czas metody pomiaru dawniej i dziś
Metody pomiaru charakterystyk przepływu ciepła
3 Metody pomiaru wybranych właściwości reologicznych płynów
A3 Metrologia metody pomiarowe
Metody pomiaru parametrów źródeł v2
1 Sprawozdanie$ 10 2014 Oscyloskopowe metody pomiaru częstotliwości i przesunięcia?zowego
Elektronika gotowe Różne metody pomiaru częstości drgań elektrycznych szczegó
Ćwiczenie 3 (Wstęp) Metody Pomiaru Rezystancji i Impedancji
Metody pomiaru trwałości warstwy granicznej olejów i smarów’’
Metody pomiaru predkosci
metody+pomiaru+w b3asno 9cci+cieplnych+ OTCQPYVK6X5X2BGZW4MVHTHGSRTET6ILEEIREIY
METODY POMIARU REZYSTANCJI1, OPOLE 13-10-1994r.
Statystyczne metody pomiarów
METODY POMIARU SKŁADU CIAŁA
więcej podobnych podstron