Sprawozdanie z laboratorium z fizyki i biofizyki
Ćwiczenie nr 1
Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego przy
użyciu wahadła matematycznego
Data wykonania ćwiczenia: 22. 04. 2008 r.
Sekcja nr 8 w składzie:
1. Andrzej Michalski
2. Robert Jała
3. Piotr Apczyński
Data oddania sprawozdania:
Ocena:
I. Wstęp teoretyczny
Nieodłącznym aspektem naszego życia jest niewątpliwie grawitacja. Przyspieszenie grawitacyjne, czyli przyspieszenie ziemskie jest powodem swobodnego spadku ciał na ziemię . Wartość przyspieszenia ziemskiego zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Wraz z wysokością przyspieszenie maleje odwrotnie proporcjonalnie do kwadratu odległości do środka Ziemi i jest wynikiem zmniejszania się siły grawitacji zgodnie z prawem powszechnego ciążenia.
Wahadło matematyczne to punktowy ciężar zawieszony na nierozciągliwej, bezmasowej nici o długości d. Wahadło będzie wykonywało ruch zbliżony do harmonicznego, pod warunkiem, że wychylimy je z położenia równowagi o niewielki kąt
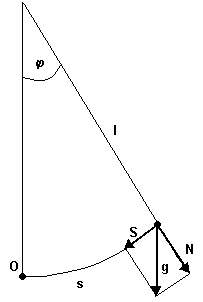
Gdy wahadło wychylone jest o kąt φ, możemy przyspieszenie g jakiego doznaje obciążnik w polu siły ciężkości rozłożyć na dwie składowe: jedną składową wzdłuż naprężonej nici N i na składową styczną do toru S (S = gsinφ). Obciążnik wahadła jest traktowany jako punkt materialny.
Gdy pewien punkt zatacza łuk, jego długość można obliczyć ze wzoru
s=lϕ gdzie:
ϕ jest kątem pomiędzy nicią, a pionem,
l jest długością nici, jak na rys. 1
Wzór na przyspieszenie styczne można zapisać w następujący sposób:
![]()
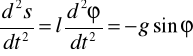
Jeśli kąty są małe możemy przyjąć: ![]()
oraz s = x
Podstawiając do równania na przyśpieszenie styczne otrzymujemy:
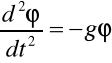
l a ponieważ s = l ϕ to: ![]()
lub ![]()
I jest to równanie ruchu harmonicznego prostego.
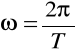
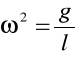
Jeśli wahadło wychylimy o mały kąt z położenia równowagi, zacznie on wykonywać drgania harmoniczne proste.
Wiedząc, iż: oraz możemy napisać równanie na okres wahań:
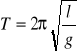
gdzie: l - długość wahadła; g - przyspieszenie ziemskie
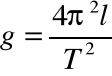
Stąd przyspieszenie ziemskie możemy obliczyć z następującego wyrażenia:
II. Przebieg ćwiczenia
1. Opis wykonywanych czynności:
W sali laboratoryjnej mieliśmy do dyspozycji 3 wahadła matematyczne.
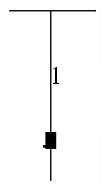
W pierwszym etapie ćwiczenia ustawiliśmy długość l drucika na długość 111 cm.
Następnie wychyliliśmy wahadło o mały kąt, który wynosił u nas 5o i wprowadziliśmy wahadło w ruch harmoniczny.
Odmierzaliśmy stoperem czas potrzebny do 70 wahnięć wahadła
Powtórzyliśmy tę czynność pięciokrotnie.
Po zanotowaniu czasów zmieniliśmy długość drucika do 142 cm.
I również tak jak w poprzednim etapie ćwiczenia wprowadziliśmy wahadło w ruch harmoniczny odchylając je o kąt 5o i puszczając.
Odmierzyliśmy stoperem czas potrzebny do 70 wahnięć i powtórzyliśmy czynność pięciokrotnie. Zanotowaliśmy wyniki.
2. Tabele pomiarów:
a) l1 = 111 cm
Ilość wahnięć: 70
Lp |
Długość l [ m ] |
Czas t potrzebny do 70 wahnięć [s] |
Okres T1 [ s ] |
1 |
1,11 |
148,14 |
2,12 |
2 |
1,11 |
148,49 |
2,12 |
3 |
1,11 |
148,74 |
2,12 |
4 |
1,11 |
147,96 |
2,11 |
5 |
1,11 |
148,32 |
2,12 |
b) l2 = 142 cm
Ilość wahnięć: 70
Lp |
Długość l [ m ] |
Czas t potrzebny do 70 wahnięć [s] |
Okres T2 [ s ] |
1 |
1,42 |
167,12 |
2,39 |
2 |
1,42 |
166,35 |
2,38 |
3 |
1,42 |
166,87 |
2,38 |
4 |
1,42 |
167,62 |
2,39 |
5 |
1,42 |
166,97 |
2,39 |
3. Obliczenia:
Z danych zebranych w tabeli powyżej obliczamy średni okres drgań T za pomocą wzoru:
![]()
- Dla l1 = 111 cm => T1 = 2,12 [s]
- Dla l2 = 142 cm => T2 = 2,39 [s]
Obliczamy średnią długość drucika wahadła:
![]()
=> ![]()
![]()
[ cm ]
Następnie obliczamy przyśpieszenie ziemskie g:
Ponieważ: 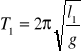
oraz 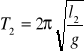
Stąd: ![]()
I po przekształceniu:
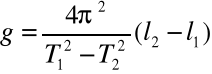
Podstawiając odpowiednie dane do wzoru obliczamy przyśpieszenie ziemskie g:
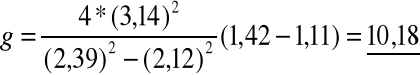
[ m/s2 ]
4. Analiza Błędów:
Błąd jest liczony za pomocą różniczki zupełnej:
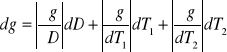
Dokładności pomiarowe dla poszczególnych elementów:
dD = 1 mm = 0,001 m
dT1 = 0,01 s
dT2 = 0,01 s
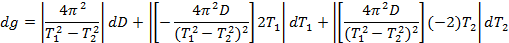
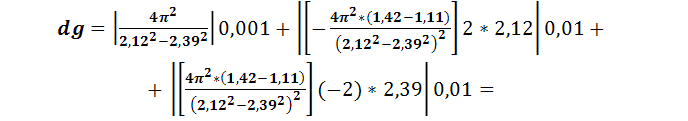
0,73
5. Wynik końcowy:
g = 10,18 ![]()
0,73 [ ![]()
]
III. Wnioski
Dzięki doświadczeniu przekonujemy się, że wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego jest możliwe, ponieważ jak wynika ze wzoru na okres drgań T wahadła matematycznego nie zależy on od masy, ani amplitudy, a jedynie od długości wahadła.
Według dokładnych pomiarów przyśpieszenie ziemskie wynosi 9,81 m/s2. Wynik naszego doświadczenie nieznacznie odbiega od tej liczby, jednakże mieści się w granicach błędu. Wpływ na tę niedokładność miało kilka czynników:
Wahadło matematyczne dostępne w laboratorium nie było zawieszone na nieważkiej nici, lecz na metalowym cienkim druciku, które powodowało tarcie.
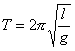
Wzór: jest ściśle słuszny jedynie w przypadku idealnym, kiedy poruszające się
wahadło nie jest narażone na żadne opory ruchu. W rzeczywistości istnieje tarcie drucika w punkcie jej zawieszenia oraz opór powietrza przeciwko ruchowi wahadła.
Podczas wychylania wahadła o kąt 5○ drucik z zawieszonym na nim odważniku bardzo drgał, co uniemożliwiało mu ruch harmoniczny przez pierwsze kilka wahnięć;
Podczas mierzenia długości drucika korzystaliśmy z metra krawieckiego, o dokładności 1mm, poza tym metr krawiecki jest bardzo giętki i te dwie przyczyny są kolejnym czynnikiem niepewności pomiarowych;
Stoper którym odmierzaliśmy czas posiadał dokładność 0,01 sekundy, do tego dochodził nasz refleks podczas startu i wyłączania stopera, a nawet ułamek sekundy znacznie wpływał na wynik.
Podczas ćwiczenia można zauważyć, że im krótszy był drucik wahadła, tym krócej trwało jedno wahnięcie.
Wyszukiwarka
Podobne podstrony:
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 2, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania-biofizyka, SPRAWOZDANIE Z ĆWICZENIA Z FIZYKI MEDYCZNEJ, SPRAWOZDANIE Z ĆWICZENIA Z FIZY
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 9, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawka zrobione, F ekstynkcja i transmisja DO ODDANIA, Sprawozdanie z ćwiczenia z fizyki medycznej
sprawozdania-biofizyka, mikroobiekty-lucidakamera2, Sprawozdanie z ćwiczenia z fizyki medycznej
sprawozdania-biofizyka, sprawozdanie mikroskop, Sprawozdanie z ćwiczenia z fizyki medycznej
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 7, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 10, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania-biofizyka, 1Sprawozdanie z ćwiczenia z fizyki medycznej, Sprawozdanie z ćwiczenia z fiz
sprawka zrobione, fantom narz±du, Sprawozdanie z ćwiczenia z fizyki medycznej
SPRAWOZDANIE Z CWICZENIA NR 4, Technologia zywnosci, semestr III, chemia zywnosci
Sprawozdanie z ćwiczenia nr 2(transformator), Studia, AAAASEMIII, 3. semestr, Elektrotechnika II, Pa
sprawozdanie cwiczenie 22, studia, agrobiotechnologie
Sprawozdanie ćwiczenie 3 poprawa wspólczynnika mocy
sprawozdanie ćwiczenie 4
Sprawozdanie ćwiczenie 4
Sprawozdanie z cwiczenia nr 1 justa
sprawozdanie ćwiczenie 7
26067395 Sprawozdanie ćwiczenie 2 i 3 OC
więcej podobnych podstron