Etapy prognozowania I
Zapisujemy dane wejściowe w postaci tabeli
Sporządzamy wykres szeregu Yt
Pozbywamy się trendu wykonując operacje
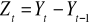
( od wartości następnej odejmujemy poprzednią )Sporządzamy wykres szereg Zt
Podejmujemy decyzje, czy szereg nie ma trendu ( wykres oscyluje w okolicach osi
OX ). Jeśli występuje trend wracamy do punktu 3Pozbywamy się wyrazu wolnego wykonując operacje
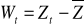
Sporządzamy wykres szeregu Wt
Liczymy autokorelacje C korzystając ze wzoru
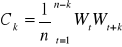
Obliczamy rk korzystając ze wzoru
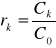
Sporządzamy wykres słupkowy szeregu rk
Sporządzamy macierz R, której elementami są wartości rk uporządkowane rosnąco, symetrycznie względem przekątnej macierzy ( na przekątnej same jedynki )
Liczymy macierz odwrotną R-1
Obliczamy macierz
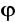
korzystając ze wzoru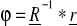
. Dla k=1 jest to część macierzy R-1 o wymiarze 1 x 1 i wartość pierwszego wiersza w macierzy r. Analogicznie dla k=2 jest to część macierzy R-1 o wymiarze 2 x 2 i wartość pierwszych dwóch wierszy w macierzy r itd.Wybieramy elementy autokorelacji cząstkowej
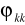
leżące na przekątnej macierzy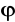
Sporządzamy wykres słupkowy szeregu
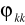
Szacujemy parametry szeregu odczytując z macierzy
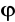
wartości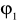
i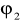
. Są to wartości powstałe z wymnożenia fragmentu macierzy R-1 i r dla k=2Powracamy do szeregu Yt podstawiając odpowiednie wartości w miejsce Zt i Wt
Prognoza na jeden okres do przodu
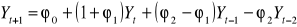
Sporządzamy wykres prognozy
Obliczamy błąd prognozy korzystając ze wzoru
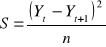
Etapy prognozowania II
Wczytujemy dane wejściowe
Jeśli szereg nie ma postaci liniowej to parametry stojące przy zmiennych objaśniających zamieniamy X'ami np.
X1=t; X2=t2; X3=t3Sporządzamy wykres tak stworzonego szeregu
Sporządzamy postać macierzową modelu
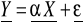
. Macierz X ma w pierwszej kolumnie same 1Obliczamy parametry strukturalne modelu korzystając ze wzoru
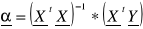
Obliczamy wartość teoretyczną
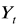
korzystając ze wzoru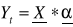
Obliczamy reszty modelu korzystając ze wzoru
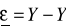
Obliczamy wariancję resztową korzystając ze wzoru
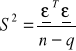
gdzie
n - liczba obserwacji
q - liczba parametrów strukturalnych modelu + 1Obliczamy macierz wariancji i kowariancji korzystając ze wzoru
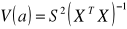
. Pierwiastek wartości leżących na przekątnej tej macierzy stanowi odchylenie standardowe reszt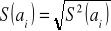
. Zapisujemy je w nawiasach pod parametrami strukturalnymi modelu
Ryzyko prognozy
![]()
Błąd średniokwadratowy
![]()
1
Wyszukiwarka
Podobne podstrony:
!!! ETAPY CYKLU PROJEKTU !!!id 455 ppt
etapy i perspektywy biotechnologii
etapy
Etapy cyklu zycia rodzinnego, ciaza
PROGNOZY GOSPODARCZE DLA POLSKI
prognozowanie 1
41 etapy rozwoju dziecka
Kawa etapy integracji
wyklad 13 Modele ARIMA w prognozowaniu (1)
Etapy planu nalotu
prognozowanie w
prognozowanie i symulacje wyklad (25 str)
Prognozowanie na podstawie modeli autoregresji
Prognoza sprzedaży
prognoza rezydentow analiza vgm
ORT Etapy organizacji imprezy turystycznej
Finanse Wycena przedsiębiorstwa i prognoza finansowa przykład (12 str )
(170 189) 11 Główne Etapy Historii Retoryki
więcej podobnych podstron