AKADEMIA GÓRNICZO - HUTNICZA
W KRAKOWIE
LABORATORIUM Z PRZEDMIOTU
PRZEWIETRZANIE I KLIMATYZACJA
Temat: WYZNACZANIE WSPÓŁCZYNNIKA OPORU LOKALNEGO (SKUPIONEGO)
Wykonali:
Tomasz Janas
Katarzyna Kornaus
IV BUDOWNICTWO
Celem ćwiczenia było zapoznanie się z wyznaczeniem strat oporu powietrza.
Przebieg ćwiczenia
W aparaturze pomiarowej umieszczane były wkładki z otworem, przez który przepływało powietrze. Mierzone było ciśnienie powietrza przed i za umieszczoną wkładką a także ciśnienie dynamiczne dla pięciu różnych prędkości przepływającego powietrza.
W celu obliczeń korzystamy z następujących wzorów:
Średnia prędkość powietrza w przekroju odcinka pomiarowego
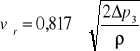
,[ m/s]
gdzie:
Δp3-ciśnienie dynamiczne
ρ-gęstość powietrza na stanowisku
Średnia prędkość powietrza w przekroju 1-4
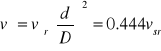
[ m/s]
gdzie:
v śr - średnia prędkość powietrza w przekroju odcinka pomiarowego
d - średnica elementu oporu skupionego
D - średnica rury
Gęstość powietrza na stanowisku pomiarowym
![]()
,[ kg/m3]
gdzie:
Ts=273,15 + ts , oC
ts - temperatura termometru suchego
e - prężność pary wodnej
e = E(tw) - Ap(ts-tw)p ,[ Pa]
Ap = 6,6225⋅10-4 , [1/oC]
E(tw) - prężność pary wodnej w stanie nasycenia
![]()
Tw=273,15+tw , [oC]
Współczynnik oporu lokalnego ξ
![]()
Parametry powietrza na stanowisku |
|
Temperatura sucha, ts |
18,8 °C |
Temperatura wilgotna, tw |
22,8 °C |
Ciśnienie barometryczne, p |
986 [Pa] |
Gęstość powietrza, ρ |
1,15 [kg/m3] |
L.p. |
Wielkości zmierzone |
Wielkości obliczone |
|||||
|
U1 |
U2 |
U3 |
vśr [m/s] |
v [m/s] |
|
współczyn. oporu skupionego ξ |
|
Δp1 [N/m2] |
Δp2 [N/m2] |
Δp3 [N/m2] |
|
|
|
|
1. de = 10 [mm] |
|||||||
1.1 |
5424,93 |
5630,94 |
245,25 |
16,90 |
0,83 |
0,22 |
14621,20 |
1.2 |
5248,35 |
5366,07 |
196,2 |
15,11 |
0,75 |
|
17170,69 |
1.3 |
4757,85 |
4708,8 |
196,2 |
15,11 |
0,75 |
|
14590,48 |
1.4 |
3973,05 |
3874,95 |
196,2 |
15,11 |
0,75 |
|
11825,97 |
1.5 |
2943 |
2943 |
98,1 |
10,69 |
0,53 |
|
18430,08 |
wartość średnia oporu dla danego de/D |
15327,68 |
||||||
2. de = 15 [mm] |
|||||||
2.1 |
3629,7 |
3678,75 |
588,6 |
26,18 |
1,29 |
0,33 |
3890,79 |
2.2 |
3384,45 |
3433,5 |
588,6 |
26,18 |
1,29 |
|
3634,82 |
2.3 |
2844,9 |
2893,95 |
490,5 |
23,90 |
1,18 |
|
3686,02 |
2.4 |
2403,45 |
2354,4 |
392,4 |
21,38 |
1,06 |
|
3609,22 |
2.5 |
1863,9 |
1863,9 |
294,3 |
18,51 |
0,91 |
|
3890,79 |
wartość średnia oporu dla danego de/D |
3742,33 |
||||||
3. de = 20 [mm] |
|||||||
3.1 |
1706,94 |
1716,75 |
981 |
33,80 |
1,67 |
0,44 |
1081,23 |
3.2 |
1667,7 |
1716,75 |
981 |
33,80 |
1,67 |
|
1105,80 |
3.3 |
1373,4 |
1324,35 |
784,8 |
30,23 |
1,49 |
|
998,30 |
3.4 |
1079,1 |
1128,15 |
833,85 |
31,16 |
1,54 |
|
867,30 |
3.5 |
784,8 |
784,8 |
441,45 |
22,67 |
1,12 |
|
1092,15 |
wartość średnia oporu dla danego de/D |
1028,96 |
||||||
4. de = 25 [mm] |
|||||||
4.1 |
686,7 |
686,7 |
1079,1 |
35,45 |
1,75 |
0,56 |
390,94 |
4.2 |
686,7 |
588,6 |
1079,1 |
35,45 |
1,75 |
|
279,24 |
4.3 |
490,5 |
490,5 |
686,7 |
28,28 |
1,40 |
|
438,81 |
4.4 |
490,5 |
490,5 |
686,7 |
28,28 |
1,40 |
|
438,81 |
4.5 |
372,78 |
313,92 |
588,6 |
26,18 |
1,29 |
|
266,21 |
wartość średnia oporu dla danego de/D |
362,80 |
||||||
5. de = 30 [mm] |
|||||||
5.1 |
294,3 |
294,3 |
1275,3 |
38,54 |
1,90 |
0,67 |
141,77 |
5.2 |
264,87 |
294,3 |
1177,2 |
37,02 |
1,83 |
|
168,94 |
5.3 |
147,15 |
196,2 |
981 |
33,80 |
1,67 |
|
153,58 |
5.4 |
196,2 |
196,2 |
784,8 |
30,23 |
1,49 |
|
153,58 |
5.5 |
147,15 |
137,34 |
588,6 |
26,18 |
1,29 |
|
133,11 |
wartość średnia oporu dla danego de/D |
150,20 |
||||||
6. de = 35 [mm] |
|||||||
6.1 |
39,24 |
58,86 |
1471,5 |
41,39 |
2,04 |
0,78 |
32,76 |
6.2 |
39,24 |
58,86 |
1373,4 |
39,99 |
1,97 |
|
35,10 |
6.3 |
29,43 |
49,05 |
1079,1 |
35,45 |
1,75 |
|
39,09 |
6.4 |
19,62 |
29,43 |
882,9 |
32,06 |
1,58 |
|
27,30 |
6.5 |
19,62 |
19,62 |
784,8 |
30,23 |
1,49 |
|
15,36 |
wartość średnia oporu dla danego de/D |
29,93 |
||||||
Dla pomierzonych i wyliczonych wielkości opracowaliśmy następujące wykresy zależności.
WNIOSKI:
Wykonanie tego doświadczenia zapoznało nas z metodą wyznaczania współczynnika oporu lokalnego, który jest wskaźnikiem start, odniesionym do średniej prędkości poza przeszkodą. Na otrzymanych wykresach nie można jednoznacznie określić zależności współczynnika oporu lokalnego od prędkości. Spodziewaliśmy się, że wraz ze wzrostem prędkości będzie malała wartość współczynnika oporu. Prawdopodobnie niedokładności pomiarowe oraz niewielka liczba odczytów (tylko 5) spowodowały odchylenia. Na podstawie ostatniego wykresu zależności współczynnika oporu lokalnego od stosunku średnic de/D możemy powiedzieć, że współczynnik ten maleje, gdy zwiększamy średnicę przeszkody (tzn. mniejszy wpływ przeszkody na ruch powietrza)
Wyszukiwarka
Podobne podstrony:
Lokalny układ współrzędnych
Opór lokalny Waldek
Opor lokalny
opór lokalny
Społecznośc lokalna
PS spolecznosc lokalna 3
Rodzina w systemie profilaktyki na szczeblu lokalnym
Srodowisko lokalne
Funkcje organizacji i stowarzyszeń społecznych w środowisku lokalnym
Opor jako reakcja na wplyw spoleczny
Organizowanie środowiska lokalnego na rzecz działalności opiekuńczo wychowawczej i pracy socjalnej p
struktura układu lokalnego
Leksykon podatków i opłat lokalnych 517 pytań i odpowiedzi
03 lokalne strategie zapewnieni Nieznany (2)
Instytucjonalne uwarunkowania rozwoju lokalnego
ekstrema lokalne
mysl lokalnie
więcej podobnych podstron