Szyjka Monika

I rok informatyki

Ćwiczenie E.2b.

Wyznaczanie oporu elektrycznego metodą mostka Wheatstone'a.

Zagadnienia teoretyczne.

Natężenie prądu i różnica potencjałów.

Jeżeli bieguny źródła połączymy przewodnikiem, to ładunki będą przepływały przez przewodnik, czyli jak mówimy potocznie, przez przewodnik będzie przepływał prąd elektryczny. Wielkością charakteryzującą prąd w przewodniku jest „natężenie prądu”.

Natężeniem prądu nazywamy stosunek ładunku przepływającego przez przekrój poprzeczny przewodnika do czasu przepływu tego ładunku. Jednostką natężenia jest amper [1A]. 1 Amper jest to natężenie takiego prądu, który przepływając przez dwa równoległe, nieskończenie długie przewodniki znajdujące się w odległości 1m od siebie w próżni, wywołuje wzajemne oddziaływanie między nimi siłą równą 210^-7 niutona na każdy metr długości.

Różnica potencjałów między dwoma punktami A i B równa jest stosunkowi pracy jaką muszą wykonać siły pola elektrycznego przy przesuwaniu ładunku z punktu A do punktu B, do wielkości tego ładunku.

Jednostką różnicy potencjałów, napięciem, jest volt (V).

Prawo Ohma.

Przy zmianach napięcia ulega zmianie natężenie prądu przepływającego przez ten przewodnik. Natężenie prądu jest zazwyczaj wprost proporcjonalne do wartości napięcia, a zatem stosunek tych dwóch wielkości jest dla danego przewodnika stały.

Powyższą zależność nazywamy prawem Ohma. Stosunek ten nosi nazwę oporu elektrycznego i jest zwykle oznaczany R. Jednostką oporu jest om (1
).

Opór przewodnika wykonanego z jednolitego materiału o stałym przekroju poprzecznym jest wprost proporcjonalny do długości przewodnika
i odwrotnie proporcjonalny do pola przekroju S:

jest współczynnikiem proporcjonalności, zależnym od materiału, zwanym oporem właściwym.

Opór właściwy jest równy liczbowo oporowi przewodnika o długości równej jednostce długości
i o polu powierzchni przekroju poprzecznego równej jednostce pola powierzchni
.

Łączenie oporników.

Przy łączeniu szeregowym natężenie prądu płynącego przez dane przewodniki jest jednakowe w każdym punkcie tych przewodników, natomiast całkowite U na przewodnikach równe jest sumie U₁ i U₂.

Szeregowe połączenie oporników.

Z założenia powyższego wynika wzór:

Po odpowiednich przekształceniach wynikających z prawa Ohma otrzymujemy zależność:

Zatem przy łączeniu szeregowym przewodników ich opór wypadkowy równa się sumie poszczególnych oporów poszczególnych przewodników.

Przy łączeniu równoległym jest spełnione równanie
.

Równoległe łączenie oporników.

W połączeniu równoległym przewodników wzór na opór wypadkowy wygląda następująco :

Otrzymane wzory dla łączenia szeregowego i równoległego, możemy uogólnić na dowolną liczbę przewodników.

Opis ćwiczenia.

Mostek Wheatstone'a to urządzenie stosowane dzisiaj w elektrotechnice oraz elektronice do szybkiego i dość dokładnego pomiaru oporu.

Prąd o natężeniu I płynący z baterii B ulega w punkcie A rozgałęzieniu. Natężenia prądów w rozgałęzieniach ADE i ACE wynoszą odpowiednio
i
.Obie te gałęzie połączone są gałęzią CD zawierającą galwanometr. Gałąź CD spina punkty C i D niby most- stąd nazwa metody. Przez gałąź CD prąd płynie albo nie zależnie od położenia suwaka czyli czy różnica potencjałów w punktach C i D jest różna od zera. Przesuwając suwak C wzdłuż rozpiętego na skali drutu AE możemy tak dobrać położenie suwaka żeby prąd nie płynął przez galwanometr. Wtedy spadek potencjału na gałęzi AD jest równy spadkowi potencjału na gałęzi AC, który oznaczamy jako
. Podobnie równe są spadki potencjału na prawych gałęziach mostka DE i CE, które oznaczamy jako
.

Stąd i z prawa Ohma mamy:

Z powyższych zależności otrzymujemy:

Ponieważ drut oporowy na całej długości ma jednakowy przekrój S i opór właściwy
, to zapisujemy:

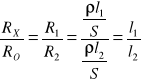
Ostatecznie :
.Posługując się tym wzorem obliczamy odpowiednie opory.

Wyniki pomiarów.

Opór nieznany	Pomiar	Opór [ ]	Długość [m]	Długość [m]	Wartość oporu [ ]	Średnia wartość oporu [ ]	Wartość oporu otrzymana ze wzoru
RX	1	60	51	49	62,45	61,02	______
		2	63	48	52			58,15
		3	65	49	51			62,45
	RY	1	60	52	48			65,00	65,19	_______
		2	63	51	49			65,57
		3	65	50	50			65,00
	RX i RY połączone szeregowo	1	120	51	49			124,90	125,13	126,21
		2	123	50,5	49,5			125,48
		3	125	50	50			125,00
	RX i RY połączone równoległe	1	30	51	49			31,22	31,53	31,517616
		2	33	49	51			31,71
		3	35	47,5	52,5			31,67

Dyskusja błędu.

Dyskusję błędu można wykonać metodą różniczkową. A zatem różniczkujemy poniższe równanie po zmiennej
:

Podstawiając odpowiednie wartości do powyższego równania otrzymujemy:
.

Stąd maksymalny błąd względny
wynosi :
.

Natomiast błąd procentowy
:

Dyskusję dla
wykonujemy analogicznie do powyższego przykładu i tak :

Stąd maksymalny błąd względny
wynosi :

Zatem maksymalny błąd procentowy
jest równy :

Dyskusję błędu dla połączenia szeregowego wykonujemy również metodą różniczkową.

Z tego równania wynika, że

.

Maksymalny błąd względny
wynosi :
,

zatem maksymalny błąd procentowy

Pozostała dyskusja błędu dla połączenia równoległego. Wykonujemy ją podobnie więc maksymalny błąd
przy połączeniu równoległym wynosi:

Stąd maksymalny błąd względny :
, a błąd procentowy

Jak widać wyniki pomiarów zarówno te bezpośrednio z pomiarów jak i obliczone ze wzoru mieszczą się w granicach wyliczonego błędu.

---