Sprawdzian nr 2
Oblicz prawdopodobieństwo:
Rzut kostką do gry:
ၗ={653421}
-wypadło mniej niż 5 oczek
A={2134 }
n(ၗ)=6
n(A)=4
![]()
1p
Prawdopodobieństwo warunkowe:
Rzut kostką do gry:
-parzysta liczba oczek
A={246}
n(A)=3
-więcej niż 3 oczka
B={456 } n(B)=3
A∩B={46} n(A∩B)=2
![]()
1p
Prawdopodobieństwo całkowite:
W urnie są 4 kule białe i 2 czarne. Losujemy jedną kulę, zwracamy ją do urny i wrzucamy jeszcze jedną kulę tego samego koloru. Następnie losujemy jedną kulę. Oblicz prawdopodobieństwo, że będzie to kula biała.
B1- w pierwszym losowaniu uzyskano białą kulę
B2- w pierwszym losowaniu uzyskano czarną kulę
A- w drugim losowaniu uzyskano białą kulę
n(ၗ)=6
n(B1)=4
![]()
![]()
![]()
![]()
P(A)=P(B1)P(A\B1)+P(B2)*P(A\B2)
![]()
0,25p
Niezależność zdarzeń
Rzut kostką do gry i monetą:
ၗ={1o, 2o, 3o, 4o, 5o, 6o, 1r, 2r, 3r, 4r, 5r, 6r}
A-parzysta liczba oczek
A={2o,4o,6o,2r,4r,6r}
n(ၗ)=12
n(A)=6
![]()
B- na monecie wypadł orzeł
B={1o, 2o, 3o, 4o, 5o, 6o } n(B)=6
A∩B={2o,4o,6o} n(A∩B)=3
Zdarzenia A i B są niezależne jeśli spełniony jest warunek:
![]()
![]()
![]()
![]()
![]()
![]()
1p
Schemat Bernoulliego
W urnie są 3 kule białe i 2 czarne. Losujemy 3 razy jedną kulę, zwracamy ją za każdym razem do urny. Jakie jest prawdopodobieństwo, że 2 razy wylosujemy kulę białą.?
A-sukces wylosujemy kulę białą
A'-porażka wylosujemy kulę czarną
n=2
k=3
![]()
![]()
![]()
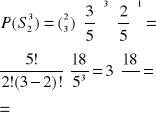
0,25p
Razem: 3,5p dostateczny
Wyszukiwarka
Podobne podstrony:
matematyka, Praw niezal1, Zdarzenie losowe
matematyka, Praw całkowite, Zdarzenie losowe
matematyka, Praw warunkowe, Zdarzenie losowe
matematyka, Schem Bernoul1, Zdarzenie losowe
matematyka, Prawdopodobieństwo, Zdarzenie losowe
Zdarzenia losowe, Matematyka, Matematyka(4)
ĆW 04, ĆW 4, Niech A i B oznaczają zdarzenia losowe
gim Zdarzenia losowe - gimnazjum, gimnazjum i podstawówka, gimnazjum, polak, matma
6 1 Zdarzenia losowe
Wlodarczyk E Zdarzenie losowe i sytuacja kryzysowa
zadania - zmienne losowe, matematyka, Matematyka. Prawdopodobienstwo i Statystyka
MATEMATYCZNA postac praw elektrostatyki
regul praw stan wyjątk 05
Kombinatoryka matematyka
więcej podobnych podstron