C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
Wykład nr 13.
13. Dynamika budowli układy o jednym dynamicznym stopniu
swobody.
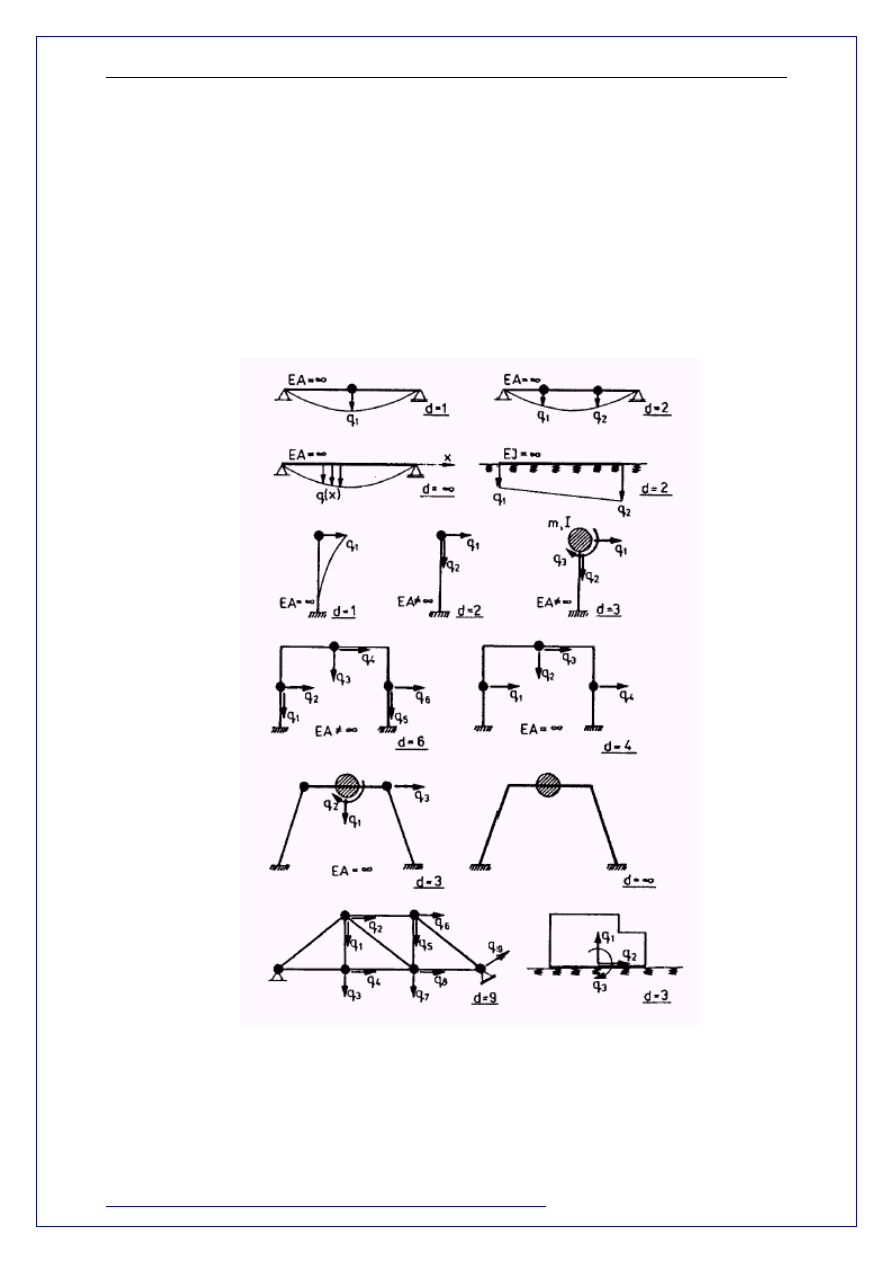
Pojęcie dynamicznego stopnia swobody zależy od sposobu rozłożenia
masy układu (masa skupiona w jednym lub kilku punktach lub rozłożona w
sposób ciągły) oraz od sztywności samej konstrukcji (EJ=
∞ lub EA=∞ dla
jednego lub kilku prętów mogą ograniczać liczbę stopni swobody).
rysunek : Mechanika Budowli ujęcie komputerowe tom 2...G.Rakowski
;
wykład 10
; 2003/2004 sem.4
W niniejszych rozważaniach zajmować się będziemy drganiami układów o
jednym stopniu swobody.
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
13.1. Drgania swobodne bez tłumienia
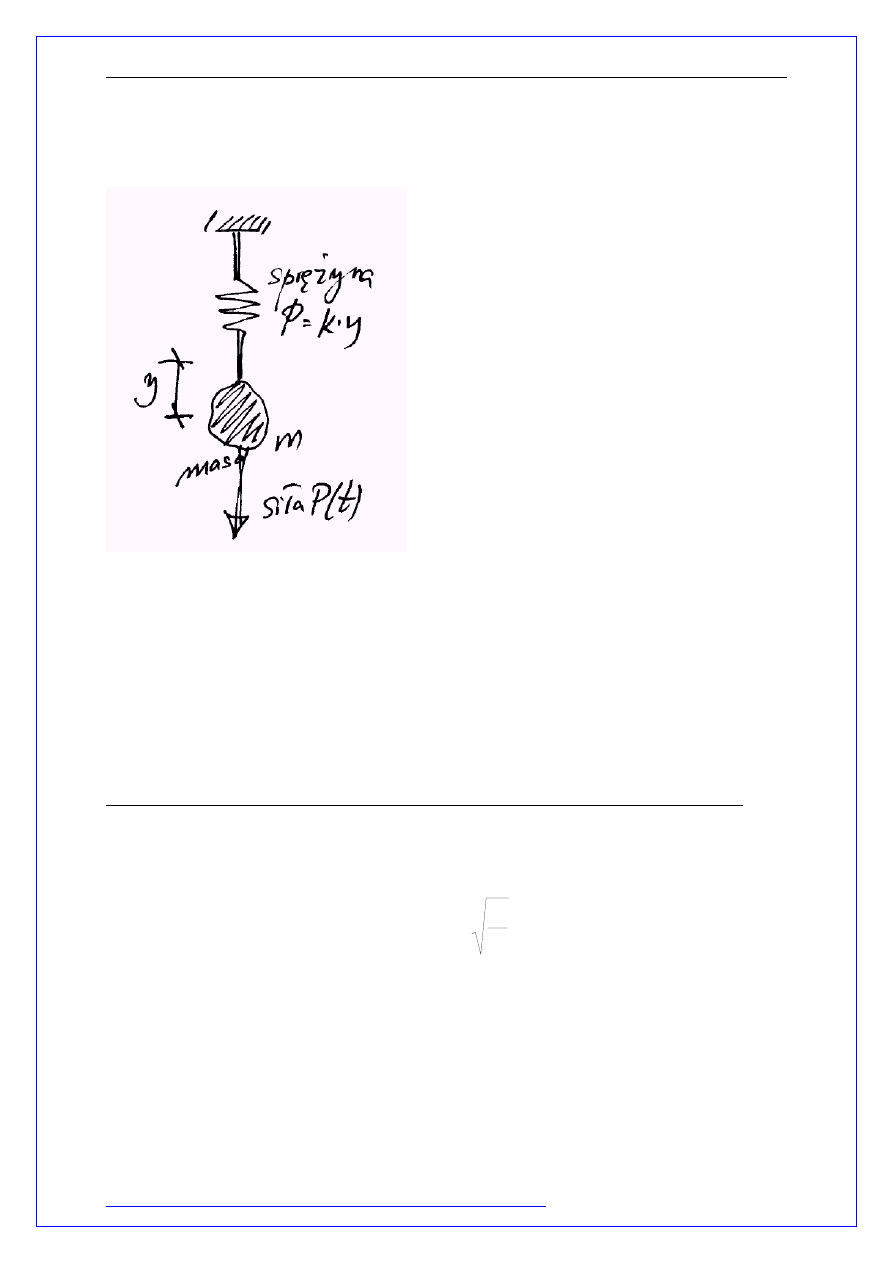
Rozpatrzmy masę m znajdującą się na
sprężynie o sztywności k.
W dowolnej chwili na ciało działają
następujące siły:
P(t) – zewnętrzna siła wymuszająca
drgania,
y
m &&
- siła bezwładności (masa
⋅
przyspieszenie),
y
c&
-siła tłumienia proporcjonalna do
prędkości ciała,
ky
-siła powstająca w sprężynie na skutek
jej wydłużenia (skrócenia)
Zmienna y(t) oznacza wychylenie ciała z
położenia równowagi statycznej a (prędkość), (przyspieszenie)
oznaczają pierwszą i drugą pochodną wychylenia względem czasu.
y&
y&&
Ogólne równanie równowagi ciała ma postać:
)
(t
P
ky
y
c
y
m
=
+
+ &
&&
jeżeli P(t)=0, to mamy do czynienia z drganiami swobodnymi,
Jeżeli , to drgania ciała są bez tłumienia (drgania swobodne).
0
=
y
c&
Równanie drgań swobodnych bez tłumienia jest więc następujące:
0
=
+ ky
y
m &&
jeżeli w powyższej zależności wprowadzimy stałą , która oznacza
częstość drgań własnych układu:
ω
m
k
=
ω
to równanie ma postać:
0
2
=
+
y
y
ω
&&
po podstawieniu
i po rozwiązaniu równania
charakterystycznego
rt
rt
e
r
y
e
y
2
,
=
=
&&
0
2
2
=
+
ω
r
;
wykład 10
; 2003/2004 sem.4
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
rozwiązanie równania różniczkowe ma postać:
t
B
t
A
y
ω
ω
cos
sin
+
=
jeżeli wprowadzimy następujące warunki brzegowe:
0
)
0
(
y
y
=
- wychylenie początkowe,
0
)
0
(
v
y
=
&
- prędkość początkowa, to stałe A i B możemy wyrazić w
funkcji powyższych warunków brzegowych:
,
0
y
B
=
ω
0
v
A
=
.
Po podstawieniu stałych równanie ma postać:
t
y
t
v
y
ω
ω
ω
cos
sin
0
0
+
=
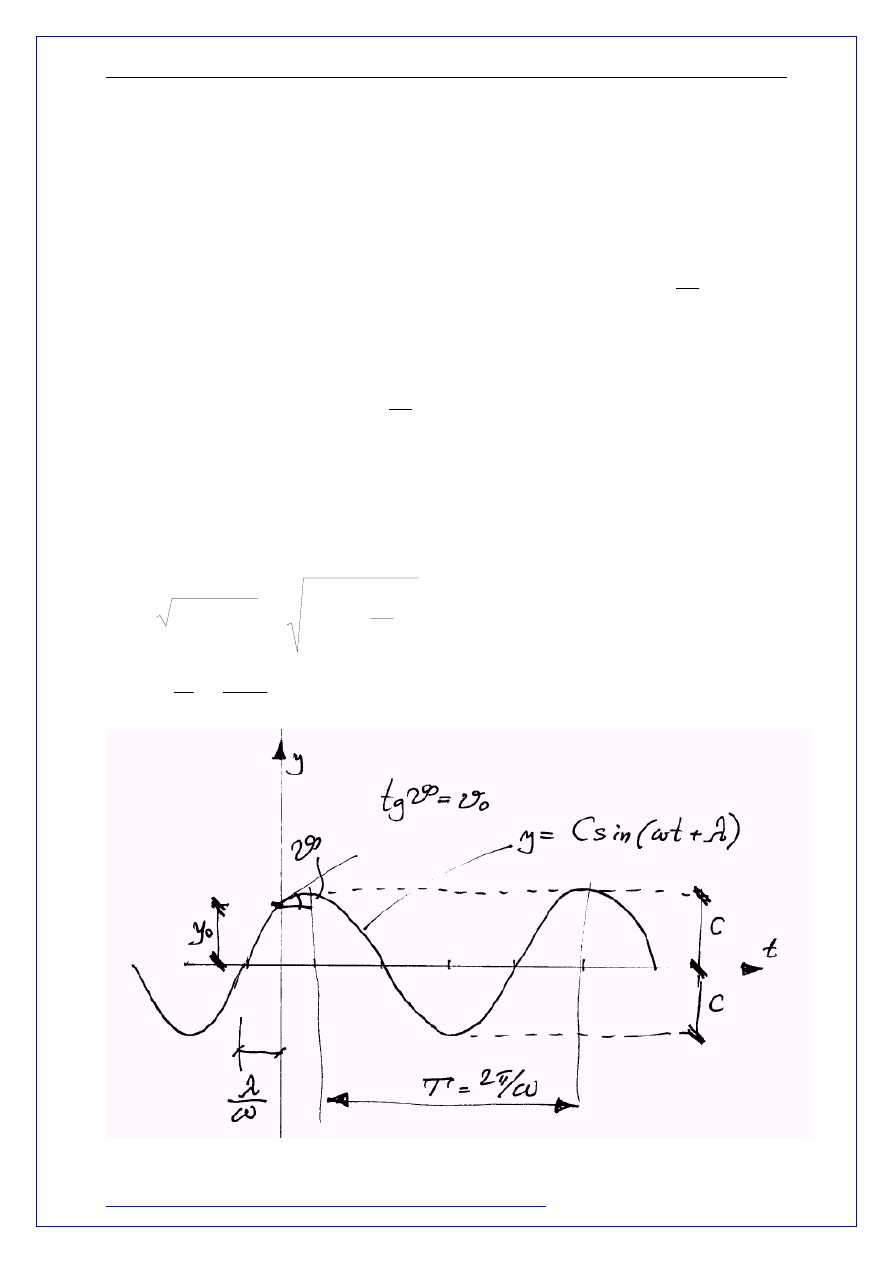
Funkcja powyższa może być również zapisana następującym wzorem:
)
sin(
λ
ω
+
=
t
C
y
gdzie :
2
0
2
0
2
2
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
ω
v
y
B
A
C
,oznacza amplitudę drań,
0
0
v
y
A
B
tg
ω
λ
=
=
jest kątem przesunięcia fazowego
;
wykład 10
; 2003/2004 sem.4
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
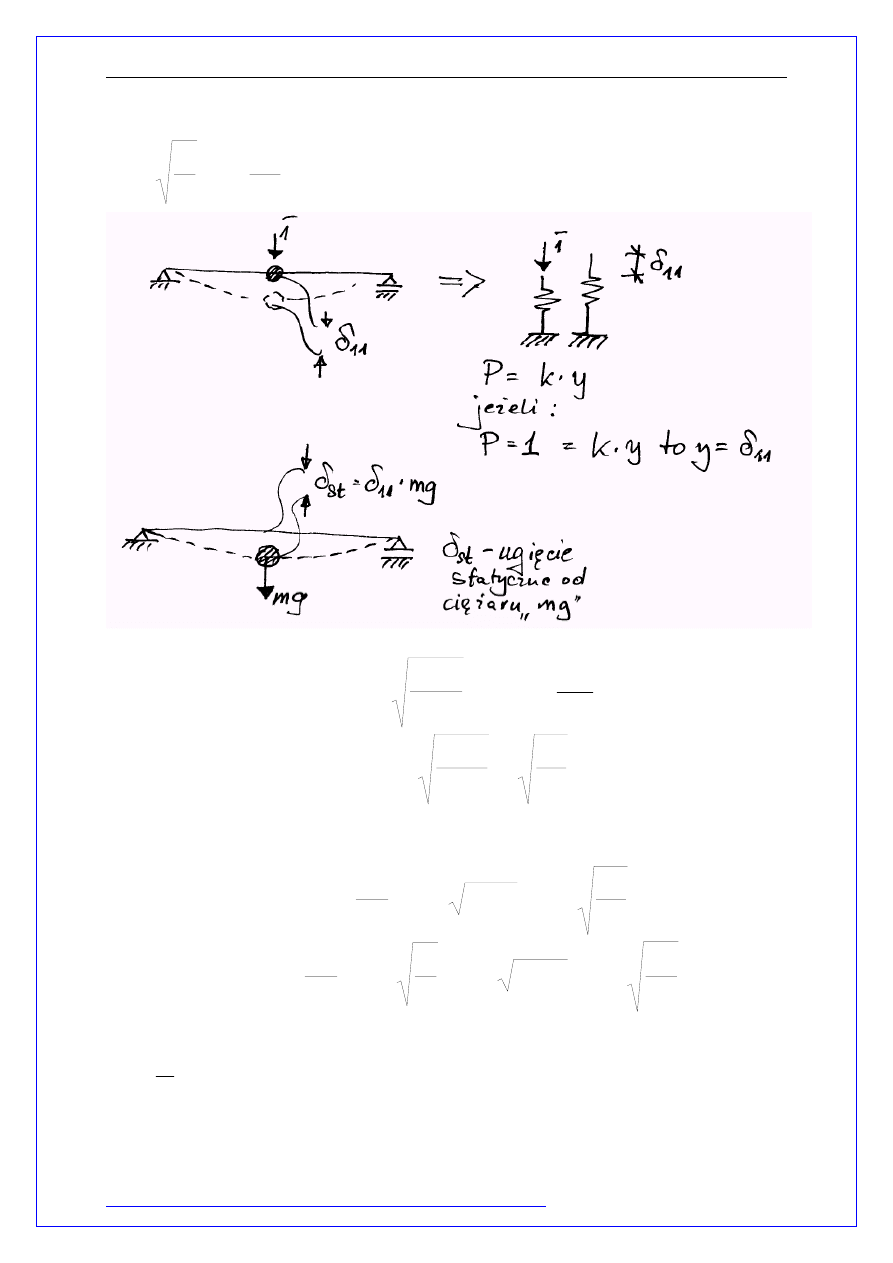
Podstawową charakterystyką drgań swobodnych jest częstość kołowa
drgań
ω
, którą można wyznaczać również z następujących zależności:
11
1
,
δ
ω
=
=
k
m
k
11
1
δ
ω
m
=
,
mg
st
δ
δ
=
11
st
st
g
m
mg
δ
δ
ω
=
=
T oznacza okres drgań:
g
m
T
st
δ
π
δ
π
ω
π
2
2
2
11
=
=
=
g
m
k
m
T
st
δ
π
δ
π
π
ω
π
2
2
2
2
11
=
=
=
=
w praktyce stosuje się też wielkości:
;
wykład 10
; 2003/2004 sem.4
]
[
1
Hz
T
f
=
-częstość fizyczna,
n=60/T –częstość techniczna
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
;
wykład 10
; 2003/2004 sem.4
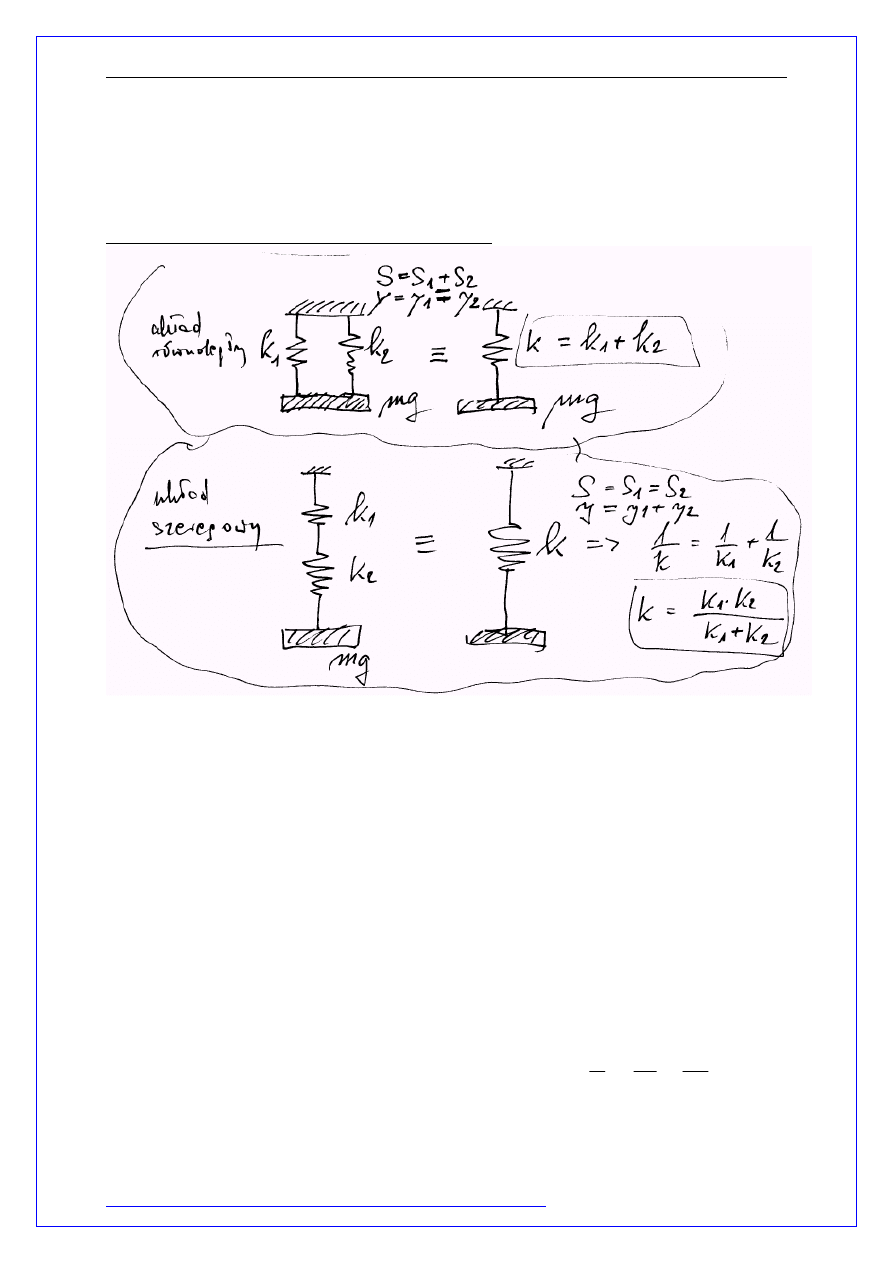
W praktyce elementy konstrukcyjne współpracują ze sobą. Połączenie
elementów konstrukcji, w którym we wszystkich częściach są takie same
przemieszczenia nazywamy połączeniem równoległym, a połączenie w
którym są takie same siły połączeniem szeregowym:
ównoległy i szeregowy układ sprężyn:
R
Układ równoległy:
układ szeregowy:
2
1
2
1
2
2
1
1
2
2
1
1
2
1
2
1
k
k
k
y
k
y
k
ky
y
k
y
k
ky
y
k
P
y
k
P
ky
P
P
P
P
y
y
y
+
=
+
=
+
=
=
=
=
+
=
=
=
2
1
2
1
2
2
1
1
2
2
1
1
2
1
2
1
1
1
1
/
/
/
/
/
/
k
k
k
k
P
k
P
k
P
k
P
k
P
k
P
y
k
P
y
k
P
ky
P
P
P
P
y
y
y
+
=
+
=
+
=
=
=
=
=
=
+
=
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
;
wykład 10
; 2003/2004 sem.4
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
;
wykład 10
; 2003/2004 sem.4
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
;
wykład 10
; 2003/2004 sem.4
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
13.2. Drgania swobodne tłumione
Równanie równowagi ciała o masie m ma postać:
)
(t
P
ky
y
c
y
m
=
+
+ &
&&
przy założeniu że nie działa siła zewnętrzna P(t):
0
=
+
+
y
m
k
y
m
c
y
&
&&
oznaczanąc:
m
k
=
2
ω
m
c
=
α
2
otrzymamy równanie:
jeżeli założymy:
to otrzymamy równanie charakterystyczne:
Rozwiązanie tego równania zależy od:
0
2
2
=
+
+
y
y
y
ω
α
&
&&
rt
rt
rt
e
r
y
re
y
e
y
2
,
,
=
=
=
&&
&
0
2
2
2
=
+
+
rt
rt
rt
e
re
e
r
ω
α
0
2
2
2
=
+
+
ω
α
r
r
(
)
2
2
4
ω
α
−
=
∆
Rozpatrujemy trzy przypadki:
1.
α
ω
>
<
∆
,
0
2
2
2
2
12
2
2
2
2
ω
α
α
ω
α
α
−
±
−
=
−
±
−
=
∆
±
−
=
a
b
r
2
2
2
2
2
1
,
ω
α
α
ω
α
α
−
−
−
=
−
+
−
=
r
r
znaczamy:
1
2
1
1
,
ω
α
ω
α
i
r
i
r
−
−
=
+
−
=
o
2
2
1
α
ω
ω
−
=
gdy
ównanie opisujące wychylenie ciała przyjmuje postać:
α
ω
>
r
;
wykład 10
; 2003/2004 sem.4
)
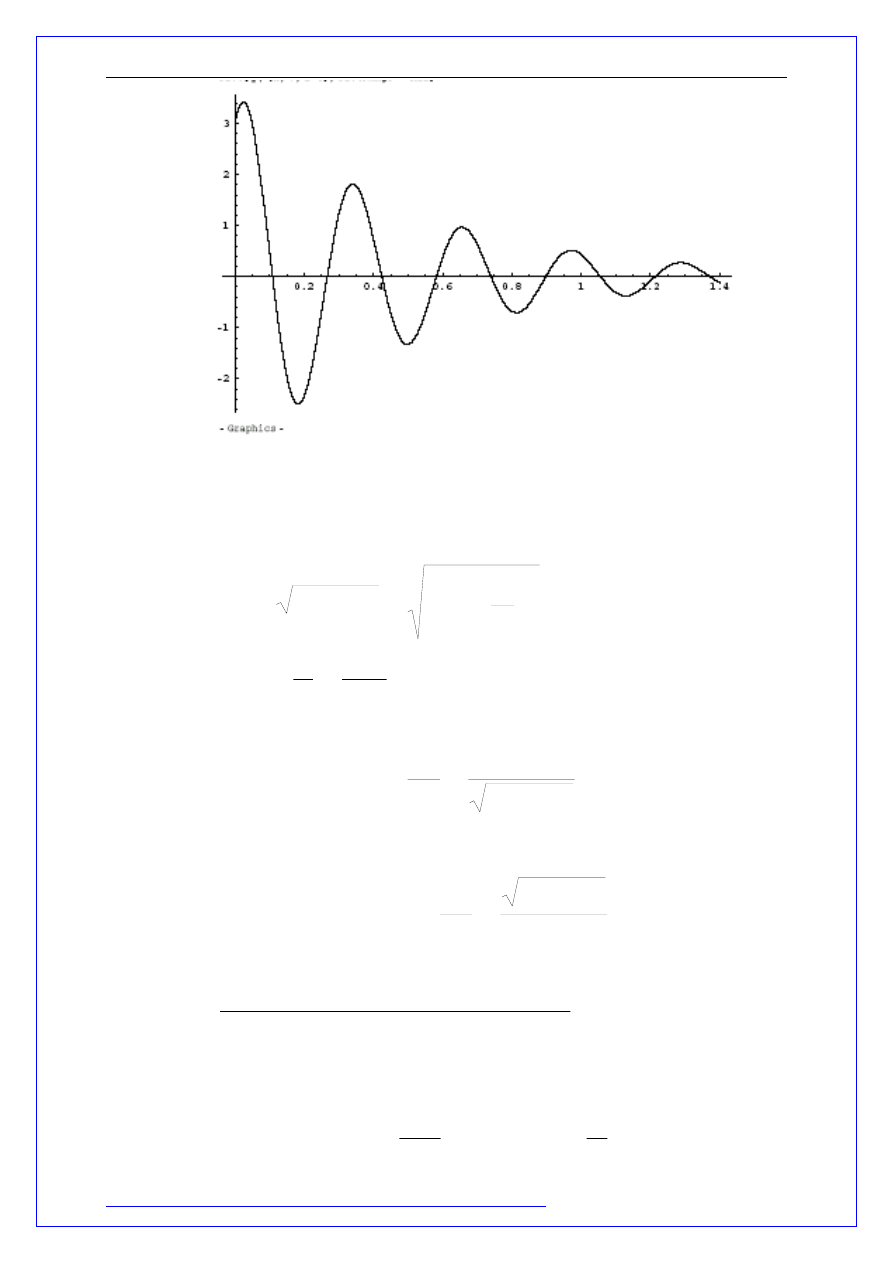
cos
sin
(
)
(
1
1
t
B
t
A
e
t
y
t
ω
ω
α
+
=
−
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
wykres y(t) od czasu
gdzie :
)
sin(
)
(
1
λ
ω
α
+
=
−
t
C
e
t
y
t
2
0
2
0
⎟
⎠
⎜
⎝
ω
2
2
⎞
⎛
+
=
+
=
v
y
B
A
C
,oznacza amplitudę drań,
0
okres
0
v
A
tg
λ
=
=
jest kątem
y
B
ω
przesunięcia fazowego
drgań zanikających:
2
2
1
2
2
α
ω
π
ω
π
−
=
=
T
częstotliwość drgań:
π
α
ω
π
ω
2
2
2
2
1
1
−
=
=
=
−
T
f
obliczamy sto
prze
y
sunek amplitud
sunięt ch o okres T
1
const
e
t
C
e
t
y
T
t
=
=
+
=
−
1
)
sin(
)
(
1
α
α
λ
ω
T
t
C
e
t
y
T
t
+
+
=
+
−
)
sin(
)
(
1
1
)
(
α
λ
ω
ω
na podstawie powyższej zależności możemy zdefiniow logarytmiczny
dekrement tłumienia:
ać
;
wykład 10
; 2003/2004 sem.4
1
1
1
ln
T
T
y
y
n
n
δ
α
α
δ
=
→
=
=
+
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
;
wykład 10
; 2003/2004 sem.4
wielkość logarytmicznego dekrementu tłumienia oraz okres drgań T
1
mogą
być wyznaczone doświadczalnie. Na ich podstawie możemy wyznaczyć
stałą tłumienia:
1
1
1
1
1
2
2
2
2
δω
π
π
δω
δ
α
m
T
m
m
T
m
c
=
=
=
=
wnioski:
•
współczynnik c tłumienia lepkiego zależy od częstości drgań
własnych
1
1
δω
π
m
c
=
•
siły tłumienia zmniejszają częstość kołową drgań
2
2
1
α
ω
ω
−
=
•
częstość drgań nie zależy od amplitudy
•
drgania tłumione mają
2.
charakter zanikający
ω
α
>
>
∆
,
0
2
2
2
2
2
1
,
ω
α
α
ω
α
α
−
−
−
=
−
+
−
=
r
r
2
2
2
ω
α
ω
−
=
gdy
ω
α
>
,
0
0
2
<
−
ω
α
2
2
1
−
=
<
+
−
=
ω
α
r
r
równanie drgań:
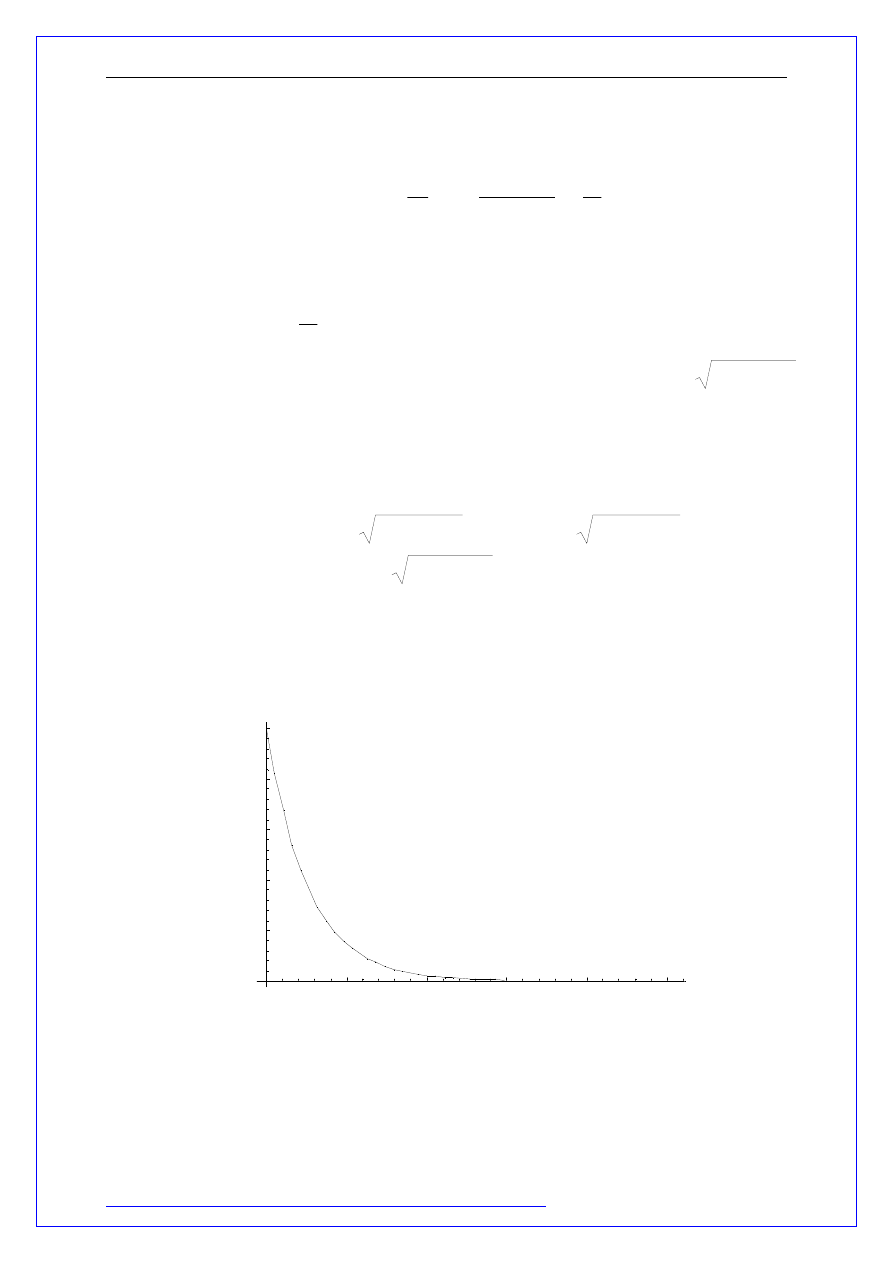
3.
t
t
De
Ce
t
y
)
(
)
(
2
2
)
(
ω
α
ω
α
−
−
+
−
+
=
ω
α
=
=
∆
,
0
0.1
0.2
0.3
0.4
0.5
1
2
3
4
5
wykres y(t) od czasu
nanie drgań :
α
α
−
=
−
=
2
1
,r
r
rów
)
(
)
(
Bt
A
e
t
y
t
+
=
−
α
C16 wykład
Mechanika Budowli I
Piotr Iwicki
http://www.pg.gda.pl/wil/dydaktyka/c16.html
Przypadek 2 i 3 tzn. gdy
ω
α
≥
nie odpowiada ruchowi drgającemu układu.
W praktyce należy je stosować gdy chcemy uniknąć drgań.
Krytyczna wartość stałej c (c
kr
) dla
ω
α
=
dana jest wzorem:
c
2
=
zamy bezwymiarowy parametr tłumienia
η
ω
m
kr
Wprowad
ω
α
ω
η
=
=
=
c
c
stąd
ηω
m
c
kr
2
α
=
η
parametr może charakteryzować tłumienia i
ą
tłu
o u
nazywany jest liczb
mienia.
P ds mowanie:
Dla
η<1,
α
ω
>
,
2
2
2
η
ω
α
ω
ω
−
=
−
=
)
cos
sin
(
)
cos
sin
(
)
(
t
B
t
A
t
B
t
A
e
t
y
t
t
ω
ω
ω
ω
α
+
+
=
−
Dla
η=1,
ω
=
)
(
)
(
Bt
A
e
t
y
+
=
−
Dla
η>1,
α
ω
<
,
1
1
1
1
1
1
e
ηω
=
−
α
,
t
α
2
2
α
ω
ω
+
−
=
)
cos
sinh
(
)
(
t
B
t
A
e
t
y
t
ω
ω
α
+
=
−
2
;
wykład 10
; 2003/2004 sem.4
2
2
Document Outline