C16 – wykład

MECHANIKA BUDOWLI I

Marek Krzysztof Jasina

13. Metoda sił – belki ciągłe, równanie trzech momentów

Metoda sił jest metodą ogólną pozwalającą rozwiązywać różnego typu układy statycznie niewyznaczalne.

Zaprezentujemy modyfikację metody sił pozwalającą rozwiązywać statycznie niewyznaczalne belki
ciągłe.

Belką ciągłą nazywamy belkę wspartą więcej niż dwu podporach, przy czym zakłada się, że jedna z
podpór jest nieprzesuwna a pozostałe przesuwne.

Belka taka jest zwykle pozioma a siły zewnętrzne i związane z nimi reakcje skierowane są pionowo.

Układ podstawowy metody sił dla belki ciągłej tworzymy zakładając przeguby nad podporami
wewnętrznymi i w utwierdzeniu, jeżeli mamy taki warunek brzegowy.

W powyższy sposób otrzymujemy bardzo korzystny z ekonomicznego punktu widzenia (prostota
schematycznego podejścia oraz mały nakładu pracy przy całkowaniu) układ złożony z belek swobodnie
podpartych.

W wyniku tego zabiegu otrzymujemy niewiadome nadliczbowe metody sił

i

X , które są momentami

zginającymi w przekrojach nad podporami, są to tzw. momenty podporowe.

Adaptacja metody sił do analizy belek ciągłych prowadzi do bardzo prostego układu równań
kanonicznych, które odniesionej do

k

-tej

podpory można zapisać w następującej postaci

1

1

1

1

1

1

1

0

6

3

6

k

k

k

k

k

k

k

k

k

k

k

k

l

l

l

l

X

X

X

EI

EI

EI

EI

δ

+

+

−

+

+

+

⎛

⎞

+

+

+

+

⎜

⎟

⎝

⎠

0

=

(13.1)

gdzie

1

k

X

−

,

k

X ,

1

k

X

+

są nadliczbowymi odpowiednio nad kolejnymi podporami

1

k

−

,

k

,

;

1

k

+

k

l ,

to rozpiętości przęseł,

1

k

l

+

natomiast

k

I ,

1

k

I

+

są momentami bezwładności belek położonych z lewej i prawej strony podpory

k

,

E jest modułem sprężystości materiału,

natomiast

0

k

δ

oznacza przemieszczenie – zmianę kąta obrotu osi belki w przekroju nad podporą od

przyczyny zewnętrznej.

k

Przyjmując oznaczenia

c

k

k

k

I

l

l

I

′ =

i

1

1

1

c

k

k

k

I

l

l

I

+

+

+

′ =

(13.2)

oraz

0

6

k

c

N

EI

0

k

δ

= −

(13.3)

wzór (13.1) można wyrazić w formie równania trzech momentów.

(

)

1

1

1

2

k

k

k

k

k

k

k

k

1

0

X

l

X

l

l

X

l

N

−

+

+

+

′

′

′

′

+

+

+

=

(13.4)

przy czym wielkość

określa się szczegółowo w zależności od rodzaju obciążenia (oddziaływania)

zewnętrznego.

0

k

N

http://www.pg.gda.pl/wil/dydaktyka/c16.html rok

2003/2004, sem. 4

C16wyklad-04d1.doc [1/3]

C16 – wykład

MECHANIKA BUDOWLI I

Marek Krzysztof Jasina

(© branicki & rakowsk)

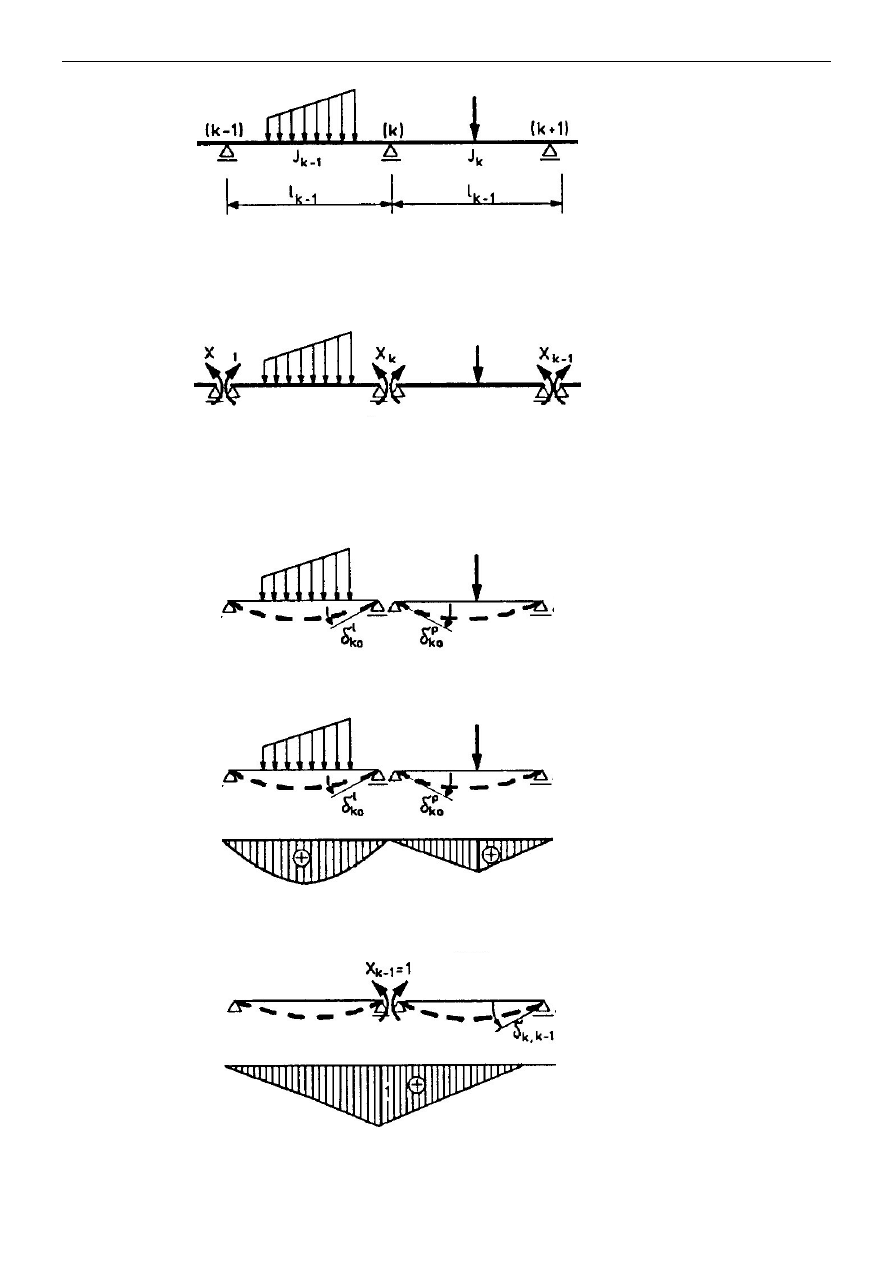
Rys. 13.1 Belka ciągła - układ wyjściowy

1

k

X

−

,

k

X ,

1

k

X

+

- nadliczbowe nad kolejnymi podporami

1

k

−

,

k

,

1

k

+

.

(© branicki & rakowsk)

Rys. 13.2 Belka ciągła - układ podstawowy metody sił

0

0

l

k

k

0

p

k

δ

δ

δ

=

+

– sumaryczna (z lewej i prawej strony podpory), zmianę kąta obrotu osi belki w przekroju

nad podporą

k

od przyczyny zewnętrznej.

(© branicki & rakowsk)

Rys. 13.3 Belka ciągła – UPMS – zmiana kąta obrotu osi belki w przekroju nad podporą

k

(© branicki & rakowsk)

Rys. 13.4 Belka ciągła – UPMS – wykresy momentów od obciążenia zewnętrznego

k

(© branicki & rakowsk)

Rys. 13.5 Belka ciągła – UPMS – wykresy momentów od obciążenia

1

1

k

X

−

=

http://www.pg.gda.pl/wil/dydaktyka/c16.html rok

2003/2004, sem. 4

C16wyklad-04d1.doc [2/3]

C16 – wykład

MECHANIKA BUDOWLI I

Marek Krzysztof Jasina

(© branicki & rakowsk)

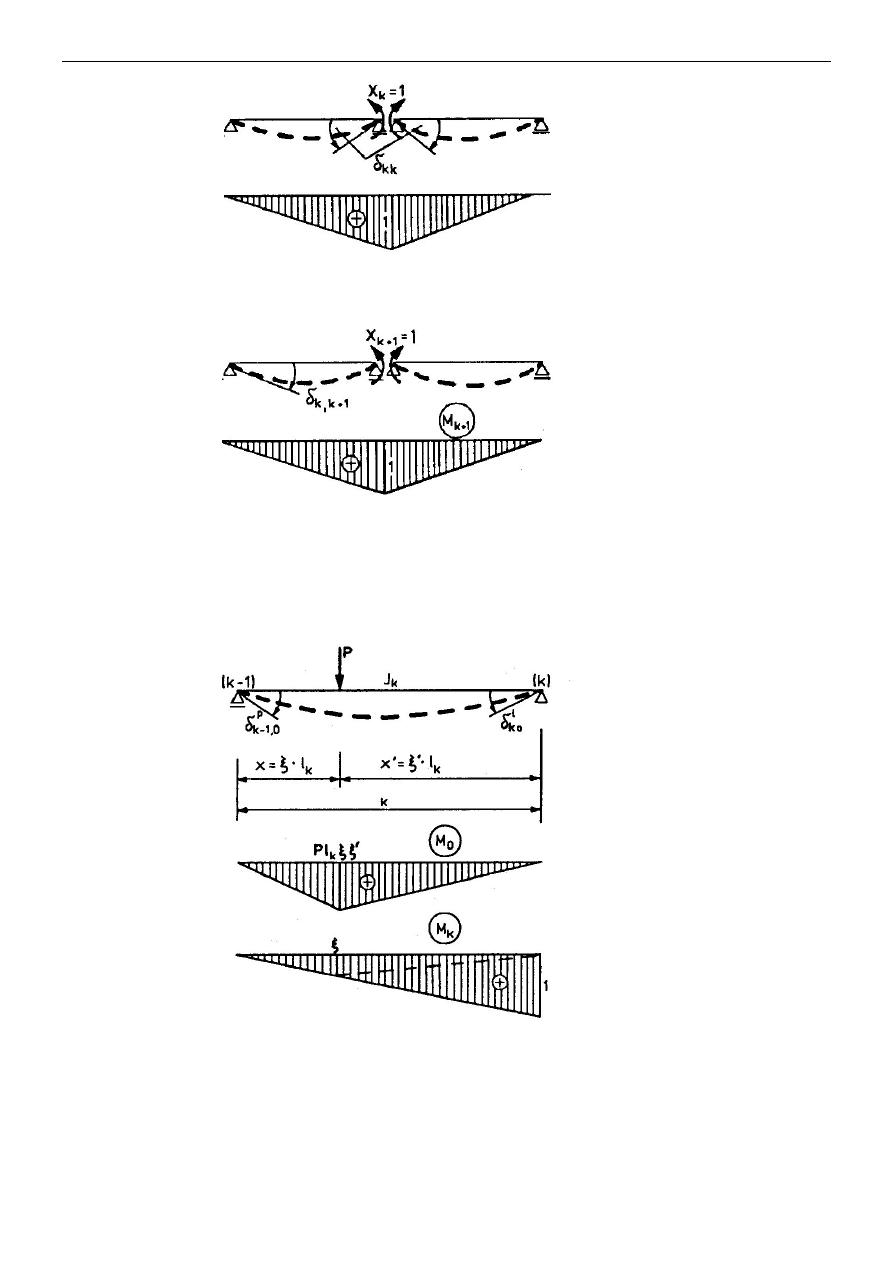
Rys. 13.6 Belka ciągła – UPMS – wykresy momentów od obciążenia

1

k

X

=

(© branicki & rakowsk)

Rys. 13.7 Belka ciągła – UPMS – wykresy momentów od obciążenia

1

1

k

X

+

=

Przykładowe wyznaczenie wielkości współczynnika prawej strony

przy obciążeniu siłą skupioną.

0

k

N

(© branicki & rakowsk)

Rys. 13.8 UPMS – wyznaczenie

0

k

N

N

kP

=

- stan obciążenia zewnętrznego

p

http://www.pg.gda.pl/wil/dydaktyka/c16.html rok

2003/2004, sem. 4

C16wyklad-04d1.doc [3/3]