1
DOMINANTA
Dominanta to wartość cechy najczęściej występująca (najpopularniejsza, najmodniejsze ⇒ moda,
wartość modalna, tryb)
Dane indywidualne
( )
x
D
- przyjmuje wartość wariantu badanej cechy, który występuje
najczęściej
Szereg rozdzielczy
ilościowy punktowy
( )
x
D
- przyjmuje wartość wariantu badanej cechy, dla którego wartość
i
n jest największa
Szereg rozdzielczy
ilościowy przedziałowy
( )
(
)
(
) (
)
1
1
1
+
−
−
−
+
−
−
+
=
D
D
D
D
D
D
D
OD
n
n
n
n
n
n
h
x
x
D
Oznaczenia:
( )
x
D
- dominanta
OD
x
- początek przedziału dominującego
D
D
D
x
x
h
0
1
−
=
- długość przedziału dominującego, obliczana jako różnica między końcem a
początkiem przedziału dominującego
D
n
- liczebność przedziału dominującego
1
−
D
n
- liczebność przedziału przed przedziałem dominującym
1
+
D
n
- liczebność przedziału następnego za przedziałem dominującym
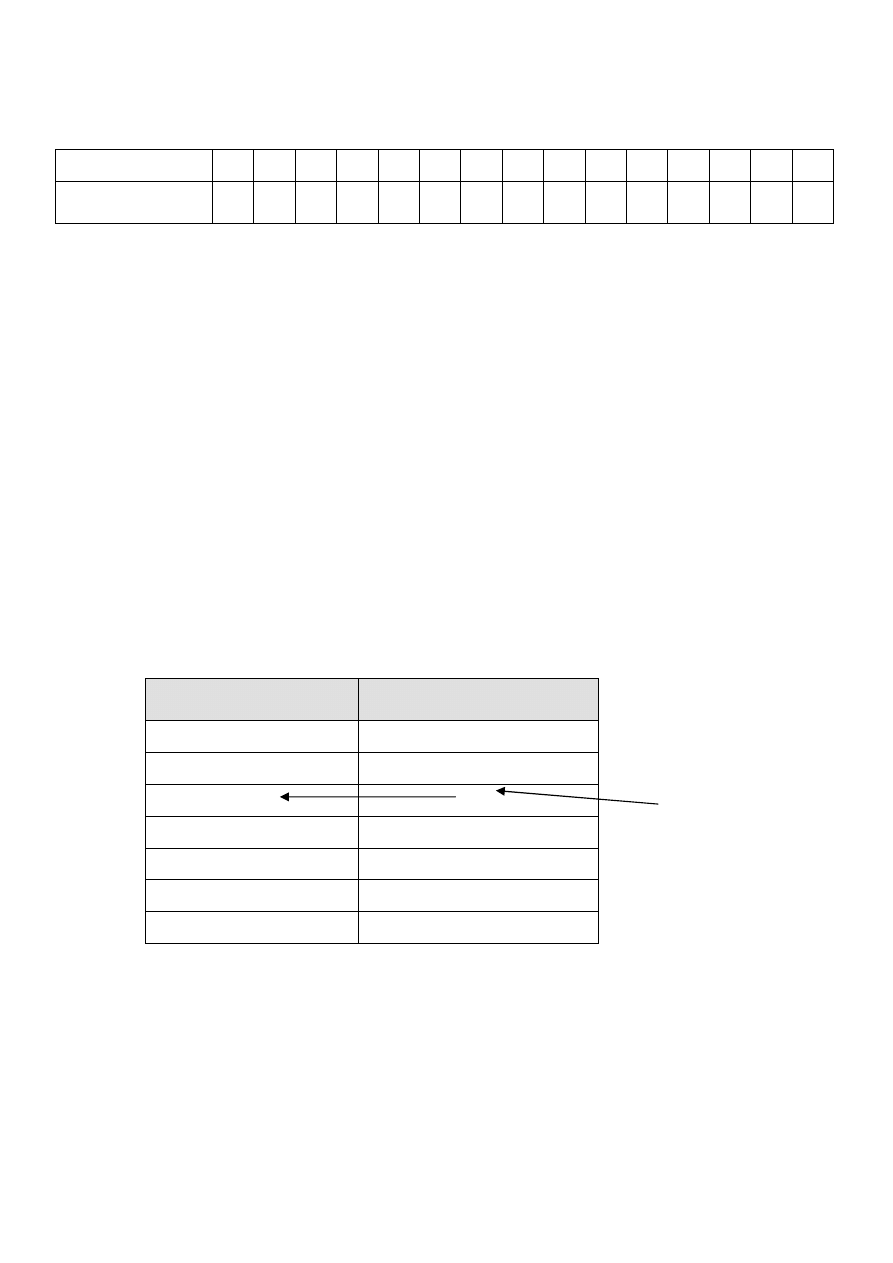
WARUNKI WYZNACZENIA DOMINANTY
NA SZEREGU ROZDZIELCZYM PRZEDZIAŁOWYM
Dominantę, na podstawie szeregu rozdzielczego ilościowego przedziałowego można obliczyć, jeśli:
o
występuje dokładnie jeden ośrodek dominujący,
o
przedział dominujący nie jest przedziałem skrajnym (ani ostatnim ani pierwszym),
o
przedział dominujący oraz przedziały sąsiednie (przedział wcześniejszy i przedział następny)
muszą mieć taką samą długość
2
Zadanie 1.
Na podstawie danych indywidualnych dotyczących długości pobytu w szpitalu pacjentów oddziału
……………………….., obliczyć i zinterpretować wartość dominanty.
Numer pacjenta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Długość pobytu w
szpitalu (w dniach)
2
3
5
6
4
5
3
2
3
2
4
3
3
4
5
•
2 dni w szpitalu spędziło 3 pacjentów
•
3 dni w szpitalu spędziło 5 pacjentów
!!!! (najwięcej pacjentów) !!!!!
( )
3
=
x
D
•
4 dni w szpitalu spędziło 3 pacjentów
•
5 dni w szpitalu spędziło 3 pacjentów
•
6 dni w szpitalu spędził 1 pacjent
Interpretacja:
Najwięcej pacjentów (5 pacjentów) spędza 3 dni w szpitalu.
Zadanie 2.
Na podstawie poniższych danych (szereg rozdzielczy punktowy) dotyczących długości pobytu pacjentów
w szpitalu, obliczyć i zinterpretować wartość dominantą.
Liczba dni pobytu
pacjentów szpitalu
Liczba pacjentów
x
i
n
i
8
max
=
i
n
1
3
2
8
3
6
4
6
5
2
SUMA
25
( )
2
2
8
max
=
⇒
=
⇒
=
x
D
x
n
i
i
Interpretacja:
Najwięcej pacjentów spędza 2 dni w szpitalu.
3
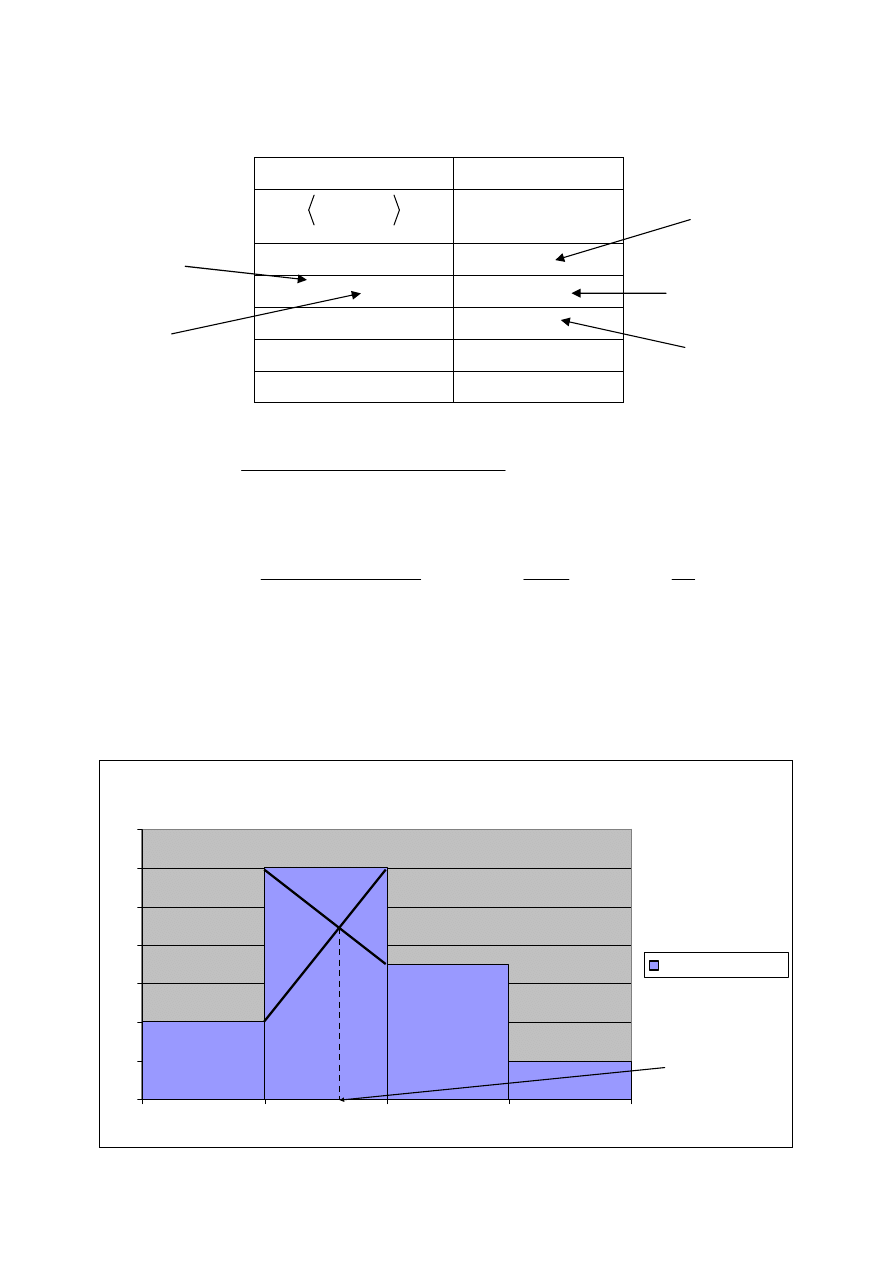
Zadanie 3.
Na podstawie poniższych danych (szereg rozdzielczy przedziałowy) dotyczących wzrostu pacjentów
przebywających w szpitalu, obliczyć i zinterpretować wartość dominanty.
D
x
0
D
x
1
wzrost (w cm)
Liczba pacjentów
1
−
D
n
12
max
=
=
D
i
n
n
1
+
D
n
i
oi
x
x
1
−
i
n
<156 – 165>
4
<166 – 175>
12
<176 – 185>
7
<186 – 195>
2
SUMA
25
( )
(
)
(
) (
)
1
1
1
+
−
−
−
+
−
−
+
=
D
D
D
D
D
D
D
OD
n
n
n
n
n
n
h
x
x
D
9
166
175
0
1
=
−
=
−
=
D
D
D
x
x
h
( )
(
)
(
) (
)
54
,
171
13
8
9
166
5
8
8
9
166
7
12
4
12
4
12
9
166
=
⋅
+
=
+
⋅
+
=
−
+
−
−
⋅
+
=
x
D
Interpretacja:
Najwięcej pacjentów ma wzrost wynoszący 171,54 cm
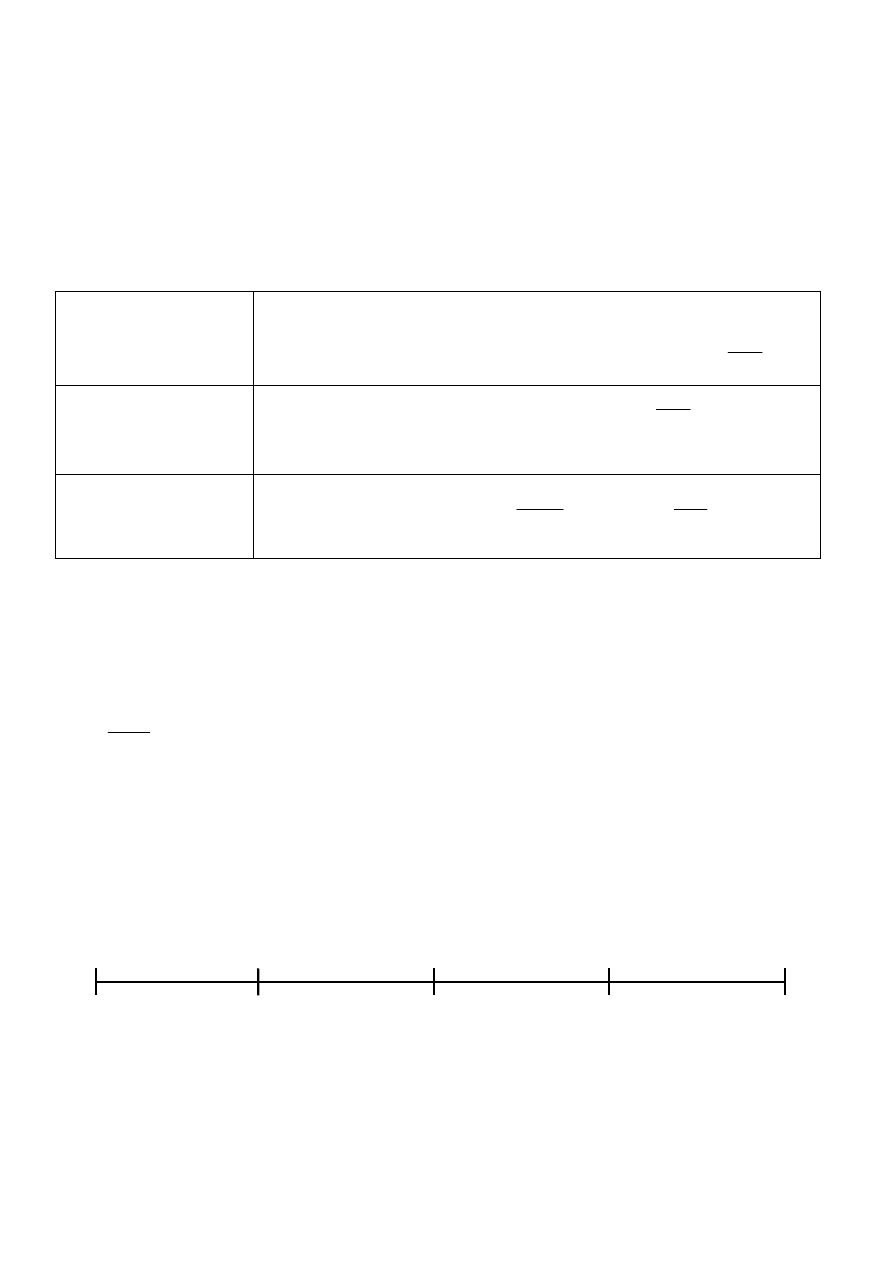
GRAFICZNE WYZNACZANIE DOMINANTY
Wzrost pacjentów przebywaj
ą
cych na oddziale ....
0
2
4
6
8
10
12
14
<156 - 165>
<166 - 175>
<176 - 185>
<186 - 195>
Liczba pacjentów
D(X)
4
MEDIANA
Mediana to wartość środkowa – wartość środkowego elementu – środkowej jednostki badania. Mediana
rozdziela badaną zbiorowość na dwie liczebnie równe części. Oznacza, że połowa badanej zbiorowości
ma wartości badanej cechy nie większe niż wartość mediany, a druga połowa badanej zbiorowości ma
wartości badanej cechy nie mniejsze niż wartość dominanty.
Dane indywidualne
( )
x
M
- po uporządkowaniu wszystkich wartości od najmniejszej do
największej, mediana przyjmuje wartość jednostki numer
2
1
+
n
Szereg rozdzielczy
ilościowy punktowy
( )
x
M
- mediana przyjmuje wartość jednostki numer
2
1
+
n
, odczytanej na
liczebnościach skumulowanych
Szereg rozdzielczy
ilościowy przedziałowy
( )
( )
M
M
MO
OM
n
h
x
F
n
x
x
M
−
+
+
=
2
1
Oznaczenia:
( )
x
M
- mediana
OM
x
- początek przedziału mediany
2
1
+
n
- numer środkowej jednostki badanej
( )
MO
x
F
- liczebność wszystkich przedziałów klasowych przed przedziałem mediany
OM
M
M
x
x
h
−
=
1
- długość przedziału mediany, obliczana jako różnica między
końcem a początkiem przedziału mediany
M
n
-
- liczebność przedziału mediany
0 %
50 %
100 %
M(x)
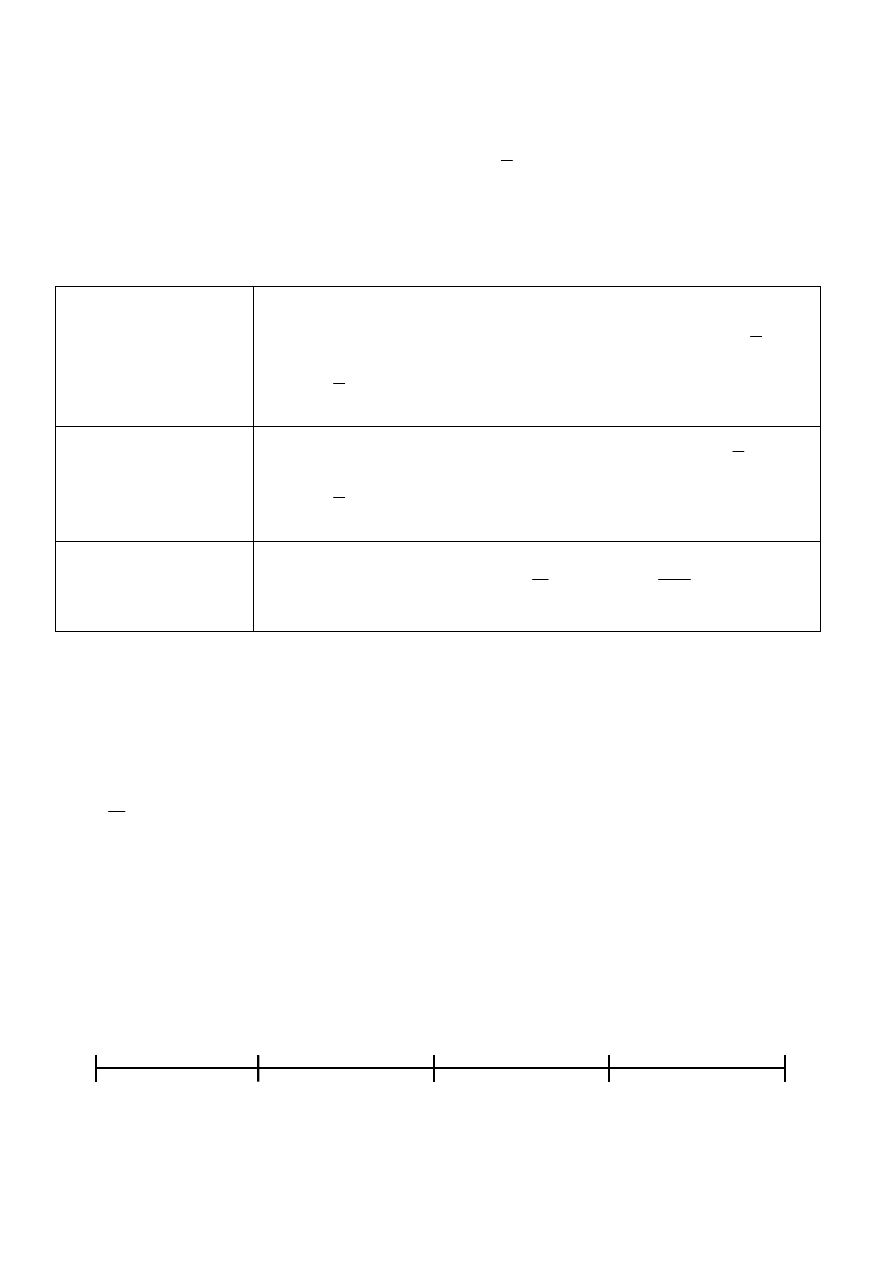
5
KWARTYL PIERWSZY
Kwartyl pierwszy to wartość jednostki badania o numerze
4
n
. Wartość kwartyla pierwszego oznacza, że
25% badanej zbiorowości ma wartości badanej cechy nie większe niż wartość kwartyla pierwszego,
a 75% badanej zbiorowości ma wartości badanej cechy nie mniejsze niż wartość kwartyla pierwszego.
Dane indywidualne
( )
x
Q
1
- po uporządkowaniu wszystkich wartości od najmniejszej do
największej, kwartyl pierwszy przyjmuje wartość jednostki numer
4
n
. Jeśli
numer
4
n
znajduje się między dwiema różnymi wartościami, to kwartyl
pierwszy przyjmie wartość wyższą.
Szereg rozdzielczy
ilościowy punktowy
( )
x
Q
1
- kwartyl pierwszy przyjmuje wartość jednostki numer
4
n
. Jeśli
numer
4
n
znajduje się między dwiema różnymi wartościami, to kwartyl
pierwszy przyjmie wartość wyższą.
Szereg rozdzielczy
ilościowy przedziałowy
( )
( )
1
1
1
1
4
1
Q
Q
OQ
OQ
n
h
x
F
n
x
x
Q
−
+
=
Oznaczenia:
( )
x
Q
1
- kwartyl pierwszy
1
OQ
x
- początek przedziału z kwartylem pierwszym
4
n
- numer jednostki wyznaczającej kwartyl pierwszy
)
(
1
OQ
x
F
- liczebność wszystkich przedziałów przed przedziałem z kwartylem pierwszym
1
1
1
1
OQ
Q
Q
x
x
h
−
=
- długość przedziału z kwartylem pierwszym, obliczana jako różnica
między końcem a początkiem przedziału z kwartylem pierwszym
1
Q
n
- liczebność przedziału z kwartylem pierwszym
0 %
50 %
100 %
M(x)
Q
1
(x)
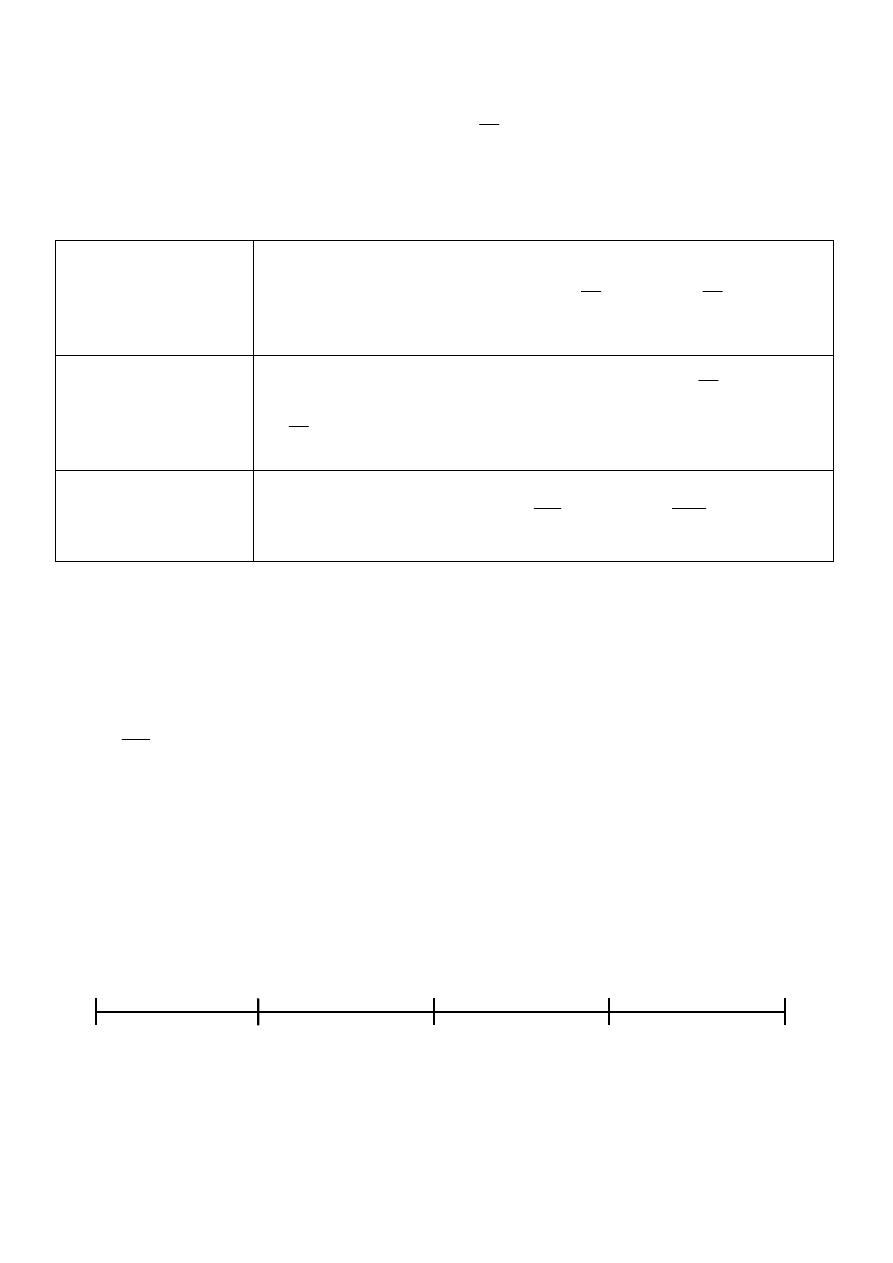
6
KWARTYL TRZECI
Kwartyl trzeci to wartość jednostki badania o numerze
4
3n
. Wartość kwartyla oznacza, że 75% badanej
zbiorowości ma wartości badanej cechy nie większe niż wartość kwartyla, a 25% badanej zbiorowości ma
wartości badanej cechy nie mniejsze niż wartość kwartyla.
Dane indywidualne
( )
x
Q
3
- po uporządkowaniu wartości od najmniejszej do największej, kwartyl
trzeci przyjmuje wartość jednostki numer
4
3
n
. Jeśli numer
4
3
n
znajduje się
między dwiema różnymi wartościami, to kwartyl trzeci przyjmie wartość
wyższą.
Szereg rozdzielczy
ilościowy punktowy
( )
x
Q
3
- kwartyl trzeci przyjmuje wartość jednostki numer
4
3
n
. Jeśli numer
4
3
n
znajduje się między dwiema różnymi wartościami, to kwartyl trzeci
przyjmie wartość wyższą.
Szereg rozdzielczy
ilościowy przedziałowy
( )
( )
3
3
3
3
4
3
3
Q
Q
OQ
OQ
n
h
x
F
n
x
x
Q
−
+
=
Oznaczenia:
( )
x
Q
3
- kwartyl trzeci
3
OQ
x
- początek przedziału z kwartylem trzecim
4
3n
- numer jednostki wyznaczającej kwartyl trzeci
)
(
3
OQ
x
F
- liczebność wszystkich przedziałów przed przedziałem z kwartylem trzecim
3
3
3
1
OQ
Q
Q
x
x
h
−
=
- długość przedziału z kwartylem trzecim, obliczana jako różnica
między końcem a początkiem przedziału z kwartylem trzecim
3
Q
n
- liczebność przedziału z kwartylem trzecim
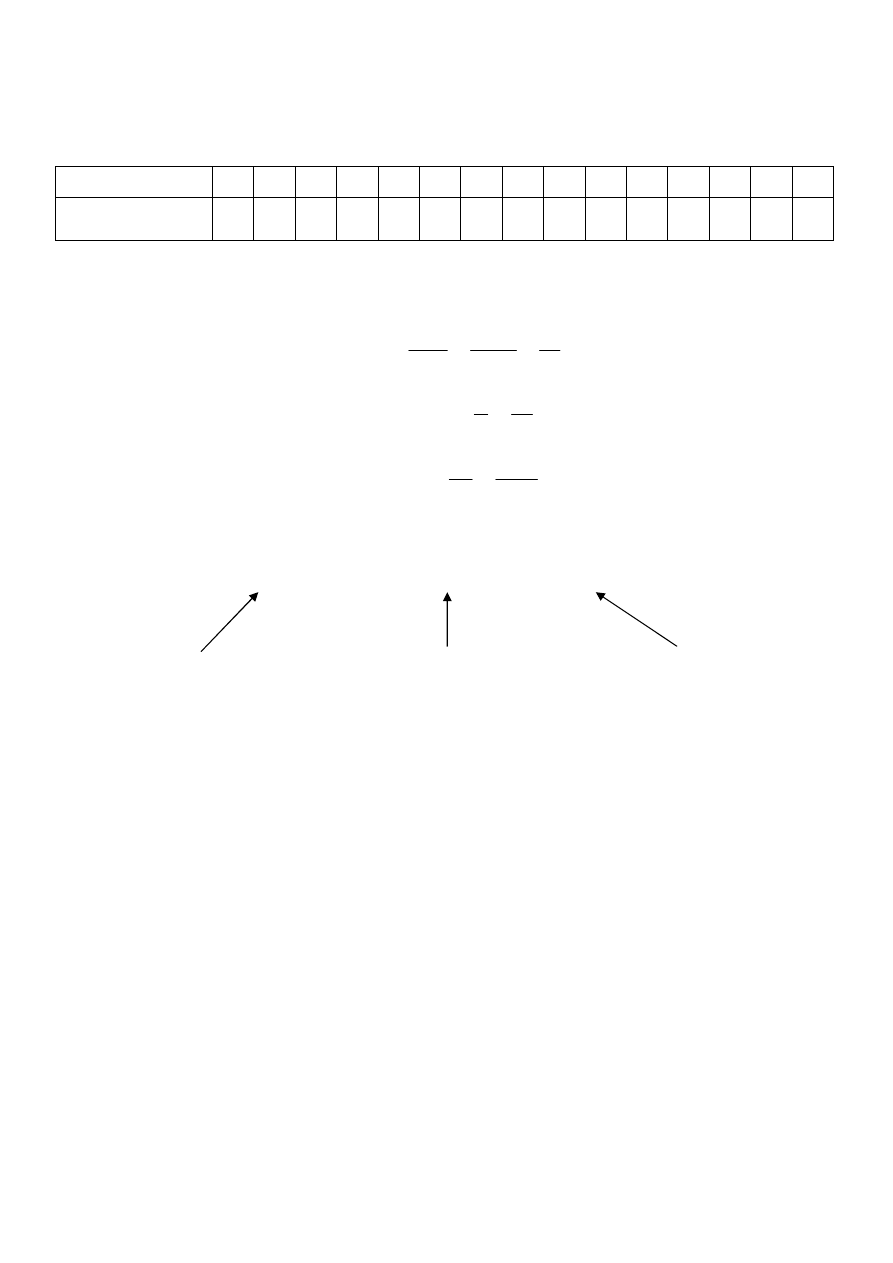
0 %
50 %
100 %
M(x)
Q
1
(x)
Q
3
(x)
7
Zadanie 1.
Na podstawie danych indywidualnych dotyczących długości pobytu pacjentów w szpitalu na oddziale
……………………….., obliczyć i zinterpretować wartość mediany, kwartyla pierwszego i kwartyla
trzeciego.
Numer pacjenta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Długość pobytu w
szpitalu (w dniach)
2
3
5
6
4
4
3
2
3
2
4
3
3
4
5
Ż
eby wyznaczyć wartość mediany, kwartyla pierwszego oraz kwartyla trzeciego, należy uporządkować
wartości badanej cechy od najmniejszego do największej.
•
Mediana ma wartość obserwacji numer
8
2
16
2
1
15
2
1
=
=
+
=
+
n
•
Kwartyl pierwszy ma wartość obserwacji numer
75
,
3
4
15
4
=
=
n
•
Kwartyl trzeci ma wartość obserwacji numer
25
,
11
4
15
3
4
3
=
⋅
=
n
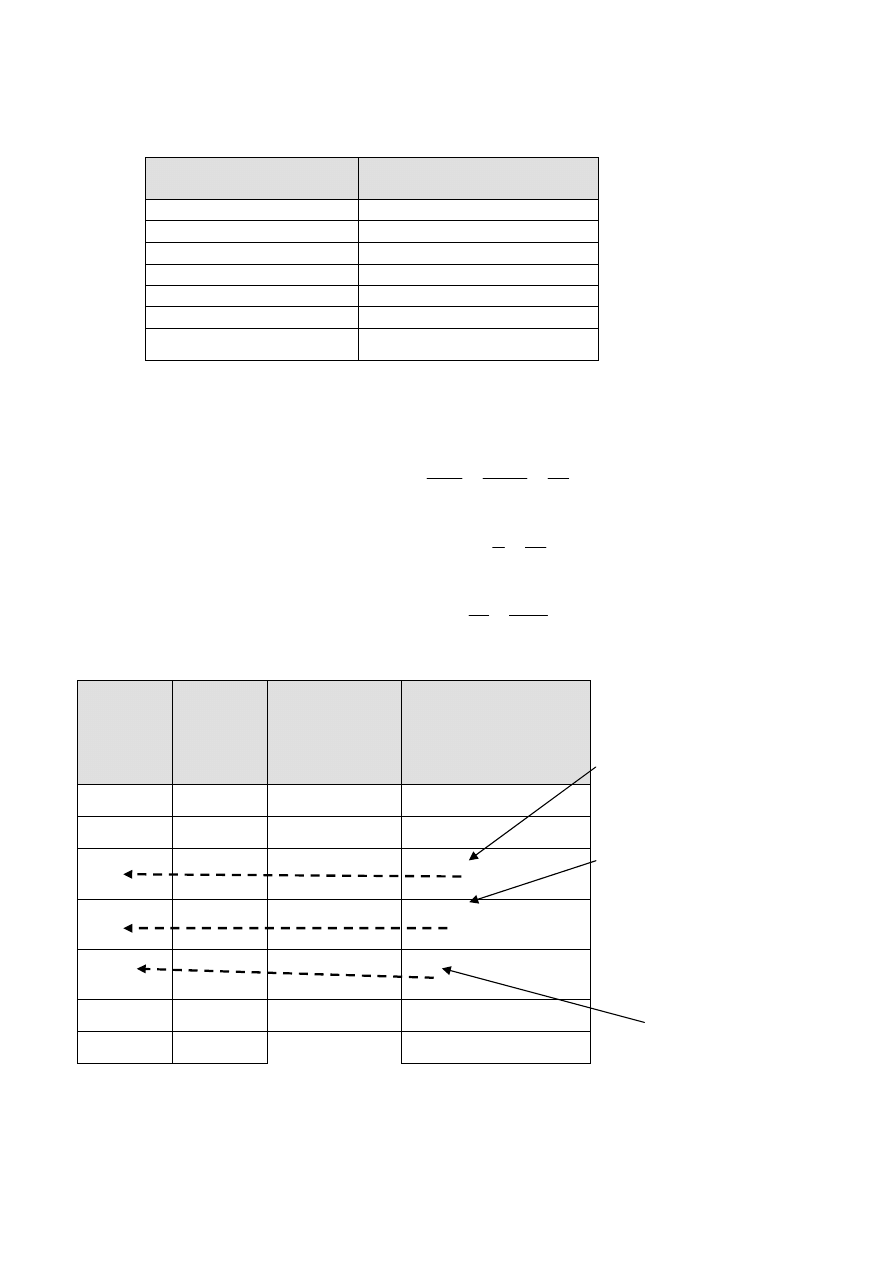
uporządkowane wartości cechy badanej (długość pobytu w szpitalu)
2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4 , 4, 5, 5, 6,
Obserwacja numer 3,75
znajduje się między
wartościami 2 i 3, więc
kwartyl pierwszy przyjmuje
wartość większą (wartość 3)
Obserwacja
numer 8 ma wartość 3,
więc mediana przyjmuje
wartość 3
Obserwacja numer 11,25
znajduje się między
wartościami 4 i 4, więc
kwartyl trzeci przyjmuje
wartość 4
( )
3
1
=
x
Q
( )
3
=
x
M
( )
4
3
=
x
Q
Interpretacje:
( )
3
=
x
M
Połowa badanych pacjentów przebywa w szpitalu nie dłużej niż 3 dni, a druga połowa
nie krócej niż 3 dni.
( )
3
1
=
x
Q
25% badanych pacjentów przebywa w szpitalu nie dłużej niż 3 dni, a 75% badanych
pacjentów nie krócej niż 3 dni.
( )
4
3
=
x
Q
75% badanych pacjentów przebywa w szpitalu nie dłużej niż 4 dni, a 25% badanych
pacjentów nie krócej niż 4 dni.
8
Zadanie 2.
Na podstawie poniższych danych (szereg rozdzielczy punktowy) dotyczących długości pobytu pacjentów
w szpitalu, obliczyć wartość mediany, kwartyla pierwszego i kwartyla trzeciego.
Liczba dni pobytu
pacjentów szpitalu
Liczba pacjentów
x
i
n
i
1
3
2
8
3
6
4
6
5
2
SUMA
25
Ż
eby wyznaczyć wartość mediany, kwartyla pierwszego oraz kwartyla trzeciego, należy wyznaczyć
liczebności skumulowane (sumowanie liczebności coraz większej liczby wariantów badanej cechy),
•
Mediana ma wartość obserwacji numer
13
2
26
2
1
25
2
1
=
=
+
=
+
n
odczytanej na liczebnościach
skumulowanych
•
Kwartyl pierwszy ma wartość obserwacji numer
25
,
6
4
25
4
=
=
n
odczytanej na liczebnościach
skumulowanych
•
Kwartyl trzeci ma wartość obserwacji numer
75
,
18
4
25
3
4
3
=
⋅
=
n
odczytanej na liczebnościach
skumulowanych
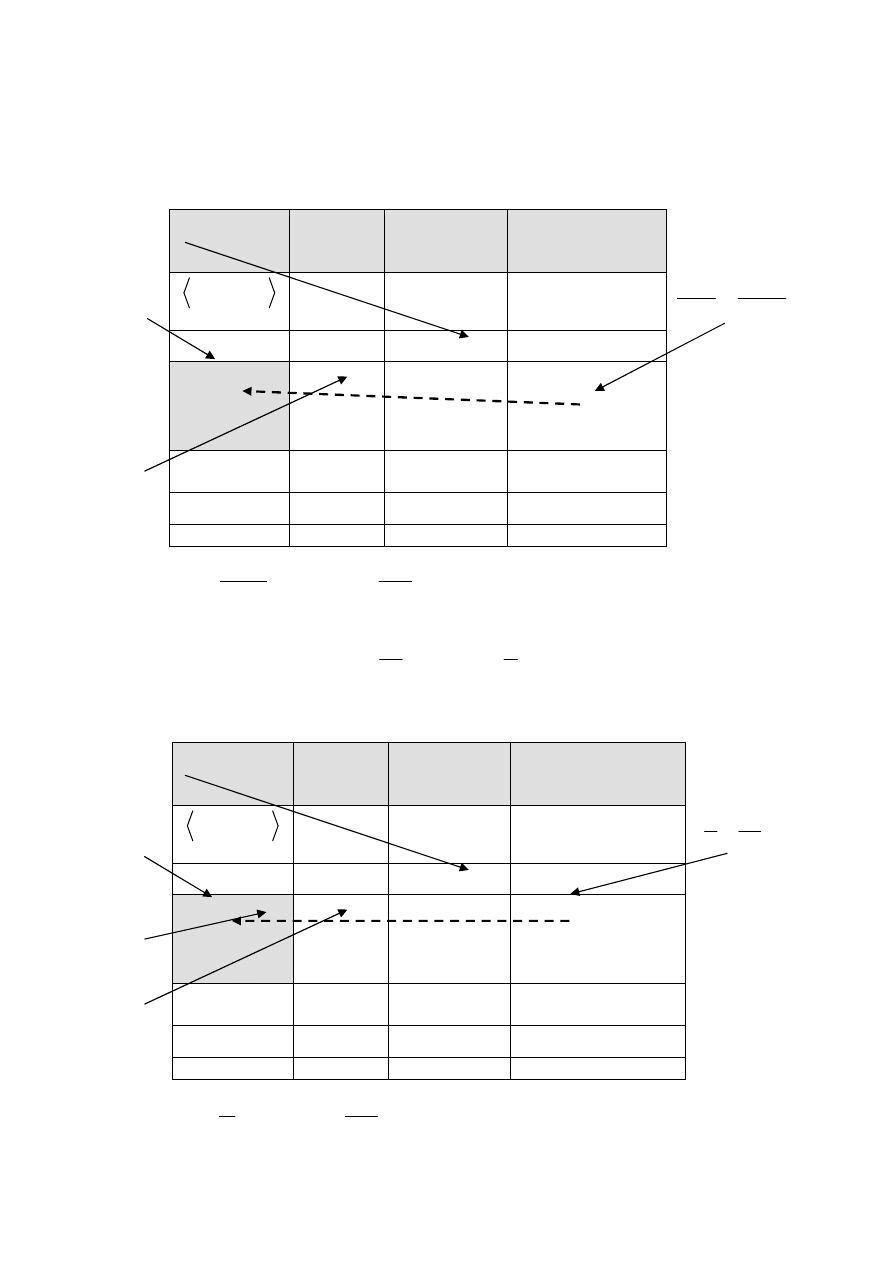
Liczba
dni
pobytu
pacjentów
szpitalu
Liczba
pacjentów
Liczebności
skumulowane
Numery pacjentów
Obserwacja numer 6,25 ma
wartość 2, więc kwartyl
pierwszy przyjmuje wartość
2
( )
2
1
=
x
Q
x
i
n
i
n
sk
1
3
3
(1, 2, 3)
Obserwacja
numer 13 ma wartość 3, więc
mediana przyjmuje wartość 3
2
8
3+8=11
(4, 5,
6, 7
, 8, 9, 10, 11)
3
6
3+8+6=17
(12,
13
, 14, 15, 16, 17)
4
6
3+8+6+6=23
(
18, 19
, 20, 21, 22, 23)
Obserwacja numer 18,75 ma
wartość 4, więc kwartyl trzeci
przyjmuje wartość
4
( )
4
3
=
x
Q
5
2
3+8+6+6+2=25
(24, 25)
SUMA
25
9
Zadanie 3.
Na podstawie poniższych danych (szereg rozdzielczy przedziałowy) dotyczących wzrostu pacjentów
przebywających w szpitalu, obliczyć i zinterpretować wartość mediany, kwartyla pierwszego kwartyla
trzeciego.
MEDIANA
)
(
OM
x
F
M
x
0
M
x
1
M
n
wzrost (w
cm)
Liczba
pacjentów
Liczebności
skumulowane
Numery
pacjentów
13
2
1
25
2
1
=
+
=
+
n
i
oi
x
x
1
−
i
n
sk
n
<156 – 165>
4
4
(1, 2, 3, 4)
<
166 –175
>
PRZEDZIAŁ
MEDIANY
12
4+12=16
(5, 6, 7, 8, 9, 10,
11, 12,
13
, 14, 15,
16)
<176 – 185>
7
4+12+7=23
(17, 18, 19, 20, 21,
22, 23)
<186 – 195>
2
4+12+7+2=25
(24, 25)
SUMA
25
( )
( )
M
M
OM
OM
n
h
x
F
n
x
x
M
−
+
+
=
2
1
9
166
175
)
1
=
−
=
−
=
M
M
M
x
x
h
( )
(
)
75
,
172
75
,
6
166
4
3
9
166
12
9
4
13
166
=
+
=
⋅
+
=
⋅
−
+
=
x
M
KWARTYL PIERWSZY
)
(
1
OQ
x
F
1
0Q
x
1
1Q
x
1
Q
n
wzrost (w
cm)
Liczba
pacjentów
Liczebności
skumulowane
Numery pacjentów
25
,
6
4
25
4
=
=
n
i
oi
x
x
1
−
i
n
sk
n
<156 – 165>
4
4
(1, 2, 3, 4)
<
166 –175
>
PRZEDZIAŁ
KWARTYLA 1
12
4+12=16
(5,
6, 7
, 8, 9, 10, 11,
12, 13, 14, 15, 16)
<176 – 185>
7
4+12+7=23
(17, 18, 19, 20, 21,
22, 23)
<186 – 195>
2
4+12+7+2=25
(24, 25)
SUMA
25
( )
( )
1
1
1
1
4
1
Q
Q
OQ
OQ
n
h
x
F
n
x
x
Q
−
+
=
9
166
175
1
1
1
0
1
=
−
=
−
=
Q
Q
Q
x
x
h
10
( )
(
)
69
,
167
69
,
1
166
4
3
25
,
2
166
12
9
4
25
,
6
166
1
=
+
=
⋅
+
=
⋅
−
+
=
x
Q
KWARTYL TRZECI
)
(
3
OQ
x
F
3
1Q
x
3
0Q
x
3
Q
n
wzrost (w
cm)
Liczba
pacjentów
Liczebności
skumulowane
Numery
pacjentów
75
,
18
4
25
3
4
3
=
⋅
=
n
i
oi
x
x
1
−
i
n
sk
n
<156 – 165>
4
4
(1, 2, 3, 4)
<166 –175>
12
4+12=
16
(5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
16)
<176 -185>
PRZEDZIAŁ
KWARTYLA 3
7
4+12+7=23
(17,
18, 19
, 20,
21, 22, 23)
<186 – 195>
2
4+12+7+2=25
(24, 25)
SUMA
25
( )
( )
3
3
3
3
4
3
3
Q
Q
OQ
OQ
n
h
x
F
n
x
x
Q
−
+
=
9
176
185
3
3
3
0
1
=
−
=
−
=
Q
Q
Q
x
x
h
( )
(
)
54
,
179
54
,
3
176
7
9
75
,
2
176
7
9
16
75
,
18
176
3
=
+
=
⋅
+
=
⋅
−
+
=
x
Q
( )
69
,
167
1
=
x
Q
( )
75
,
172
=
x
M
( )
54
,
179
3
=
x
Q
Interpretacje:
( )
69
,
167
1
=
x
Q
25% badanych pacjentów ma wzrost nie większy niż 167, 69 cm, a 75% badanych
pacjentów ma wzrost nie mniejszy niż 167,69 cm.
( )
75
,
172
=
x
M
Połowa badanych pacjentów ma wzrost nie większy niż 172,75 cm, a druga połowa
badanych pacjentów ma wzrost nie mniejszy niż 172,75 cm.
( )
54
,
179
3
=
x
Q
75% badanych pacjentów ma wzrost nie większy niż 179,54 cm, a 25% badanych
pacjentów ma wzrost nie mniejszy niż 179,54 cm.