Allel – jedna z mo

ż

liwych,

powstałych w wyniku mutacji form danego genu

Para alleli determinuje jedn

ą

cech

ę

jako

ś

ciow

ą

.

Le

żą

one naprzeciwko siebie

w

ś

ci

ś

le okre

ś

lonym miejscach (loci)

w chromosomach homologicznych

Allele dominuj

ą

ce - koduj

ą

informacj

ę

, której ekspresja w fenotypie

wyst

ę

puje równie

ż

, gdy jest w układzie heterozygotycznym

Allele dominuj

ą

ce całkowicie

– koduj

ą

cech

ę

dominuj

ą

c

ą

kompletnie

Allele dominuj

ą

ce cz

ęś

ciowo

– koduj

ą

cech

ę

dominuj

ą

c

ą

niekompletnie

DZIEDZICZENIE – PRZEKAZYWANIE CECH
Z POKOLENIA NA POKOLENIE

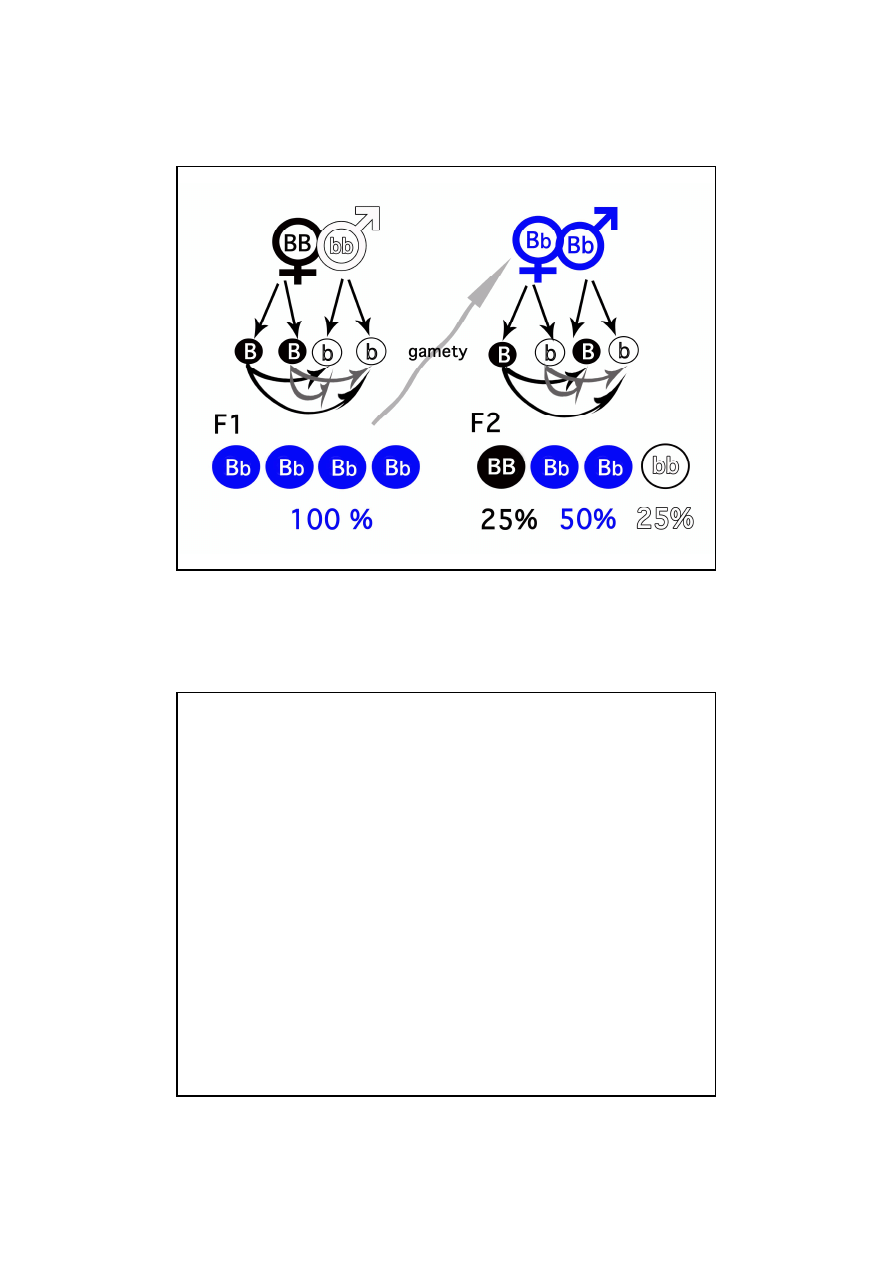
Dziedziczenie jednej cechy o dominowaniu

kompletnym (typ Pisum)

Przykład: dziedziczenie czarnego i czerwonego umaszczenia u bydła

C – gen warunkuj

ą

cy umaszczenie czarne jest dominuj

ą

cy

c – gen warunkuj

ą

cy umaszczenie czerwone jest recesywny

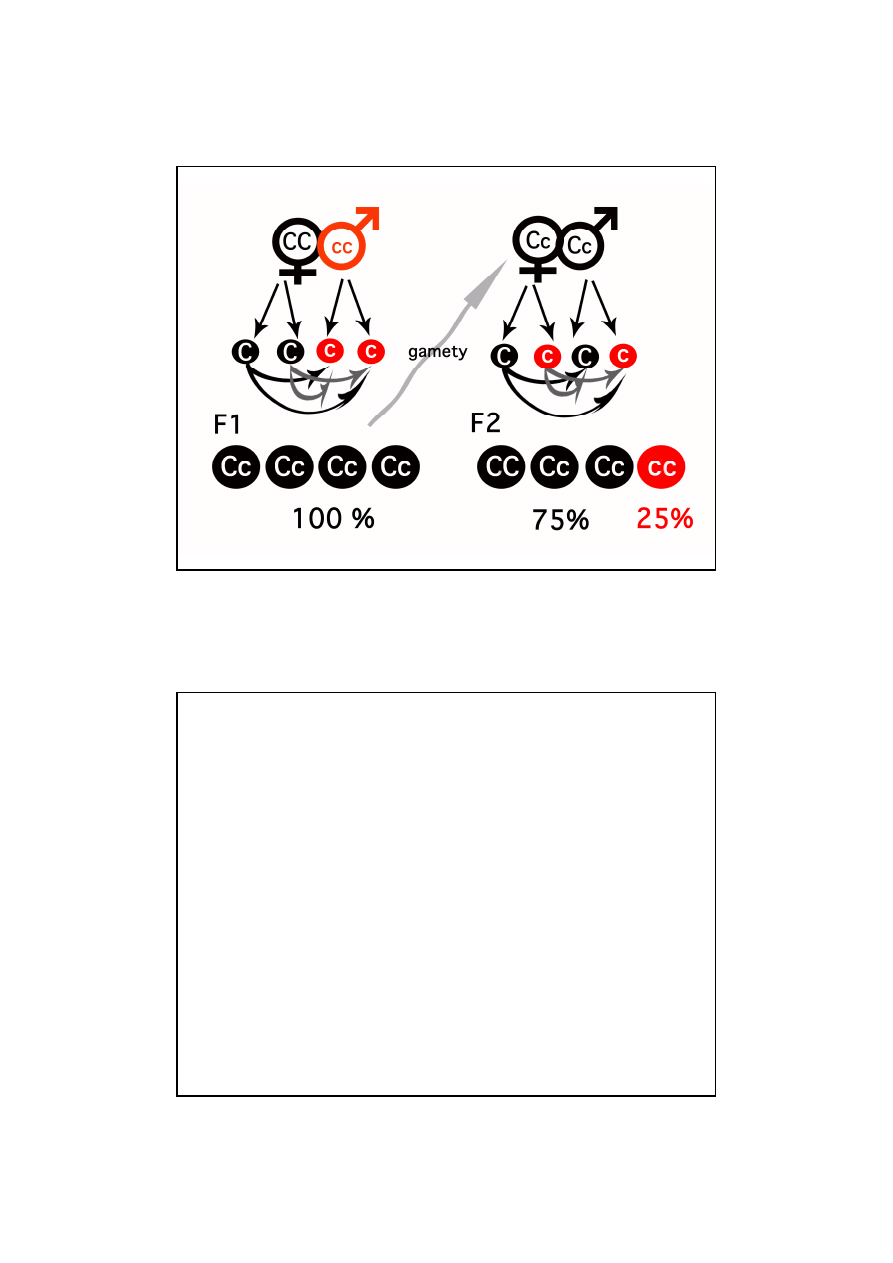
Kwadrat Punneta

Przykłady cech dziedzicz

ą

cych si

ę

w typie Pisum

BYDŁO:
- brak rogów (P) obecno

ść

rogów (p)

- umaszczenie jednolite (S) umaszczenie łaciate (s)
- głowa biała (W) głowa innej barwy (w)
- k

ę

dzierzawa sier

ść

(K) gładka sier

ść

(k)

KONIE:
- umaszczenie kare (K) umaszczenie kasztanowate (k)
- umaszczenie łaciate (Ł) umaszczenie jednolite (ł)

OWCE:
- umaszczenie białe (W) umaszczenie czarne (w)
- umaszczenie jednolite (Ł) umaszczenie pstre (ł)
- barwa pełna (C) albinizm (c)
- tłuszcz biały (W) tłuszcz

ż

ółty (w)

Przykłady cech dziedzicz

ą

cych si

ę

w typie Pisum

Ś

WINIE:

- czarny pigment skóry (B) brak pigmentu (b)
- włosy białe (W) włosy czarne (w)
- racica mułowata (M) racica normalna (m)
- brak reakcji na halotan (H) reakcja na halotan (h)

KURY:
- skóra biała (W) skóra

ż

ółta (w)

- grzebie

ń

ró

ż

yczkowaty (R) grzebie

ń

prosty (r)

- niebieska skorupa jaja (O) biała skorupa jaja (o)
- broda i baki (B) brak brody i baków (b)

Zadanie:

Jakie genotypy i fenotypy oraz w jakich proporcjach wyst

ą

pi

ą

u potomstwa:

a)Czarnych buhajów homozygotycznych i czarnych krów homozygotycznych
b)Czarnych buhajów homozygotycznych i czarnych krów heterozygotycznych
c)Czarnych buhajów homozygotycznych i czerwonych krów
d)Czarnych buhajów heterozygotycznych i czerwonych krów
e)Czeronych buhajów i czerwonych krów

DZIEDZICZENIE – PRZEKAZYWANIE CECH
Z POKOLENIA NA POKOLENIE

Dziedziczenie jednej cechy o dominowaniu

niekompletnym (typ Zea)

Przykład: dziedziczenie ubarwienia u kur rasy andaluzyjskiej

Bl – gen warunkuj

ą

cy ubarwienie czarne

– tylko w przypadku homozygoty dominuj

ą

cej (BlBl)

bl – gen warunkuj

ą

cy ubarwienie białe

– tylko w przypadku homozygoty recesywnej (blbl)

W przypadku heterozygoty cecha w fenotypie przyjmuje warto

ś

ci

po

ś

rednie – ubarwienie jest niebieskie (Blbl)

Przykłady cech dziedzicz

ą

cych si

ę

w typie Zea

BYDŁO:
- rasa shorthorn – umaszczenie: czerwone - BB, dereszowate - Bb,

białe - bb

KONIE:
-rasa palomino – umaszczenie: bladokremowe - DD, palomino - Dd,

jasnokasztanowate lub jasnogniade - dd

KOZY:
-uszy długie - UU, uszy

ś

rednie - Uu, brak uszu – uu

KURY:
- upierzenie szurpate – FF, upierzenie

ś

rednio szurpate – Ff, upierzenie

normalne – ff

Zadanie:

Jakie b

ę

dzie ubarwienie u potomstwa kur andaluzyjskich:

a)czarnych kogutów i białych kur
b)czarnych kogutów i czarnych kur
c)czarnych kogutów i niebieskich kur
d)białych kogutów i niebieskich kur
e)niebieskich kogutów i niebieskich kur

Zadanie:

Pewne stado kur andaluzyjskich składaj

ą

ce si

ę

w 50% z kur białych i w

50% z kur niebieskich, zostało skojarzone z:
a)Kogutami czarnymi,
b)Kogutami białymi,
c)Kogutami niebieskimi

Jakie fenotypy wyst

ą

pi

ą

u potomstwa I w jakich proporcjach?

Jak rozwi

ą

za

ć

zadanie w przypadku, gdy stado składa si

ę

w 25% z kur białych

i w 75% z kur niebieskich?

DZIEDZICZENIE – PRZEKAZYWANIE CECH
Z POKOLENIA NA POKOLENIE

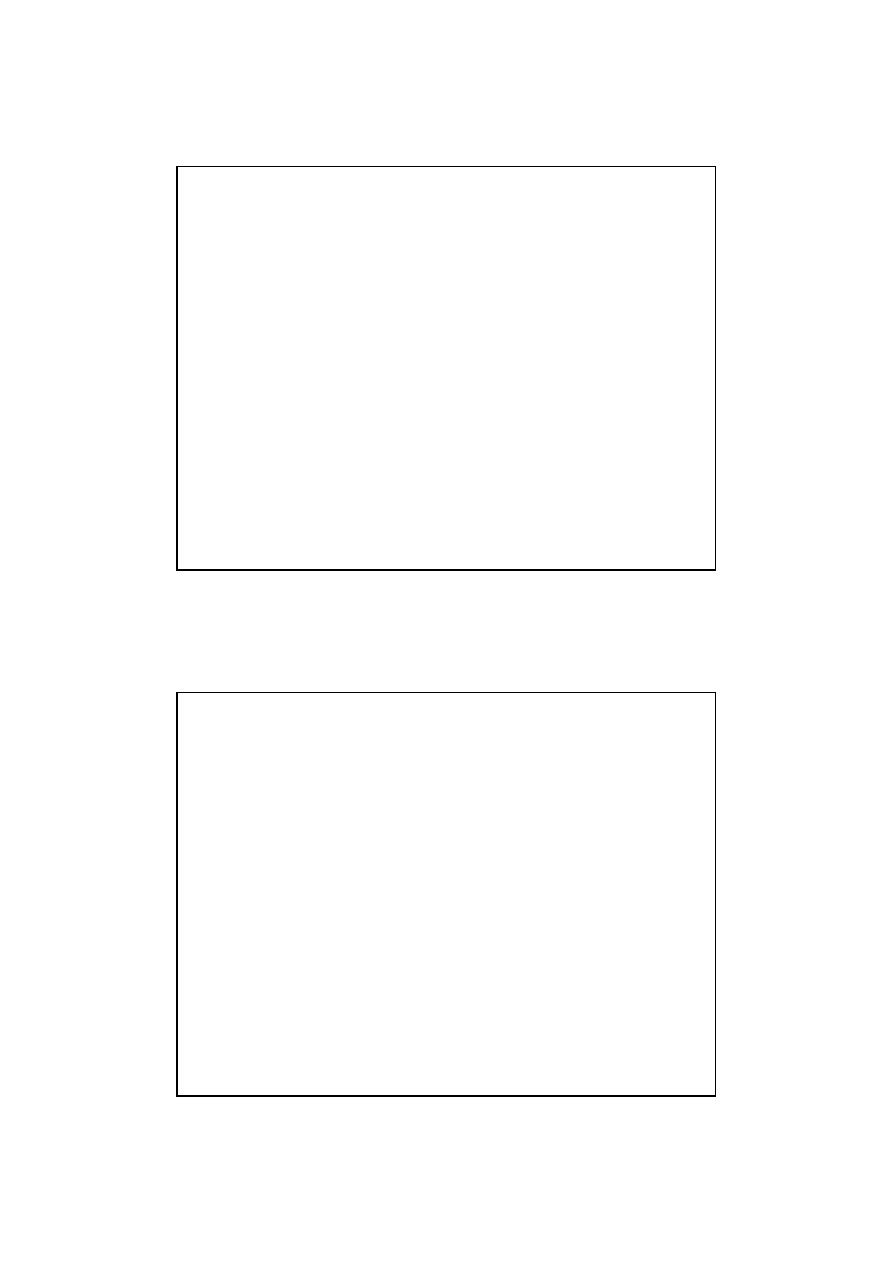
Dziedziczenie dwóch cech niezale

ż

nych o

dominowaniu

kompletnym

Przykład: dziedziczenie umaszczenia u bydła

C – gen warunkuj

ą

cy umaszczenie czarne

c – gen warunkuj

ą

cy umaszczenie czerwone

S – gen warunkuj

ą

cy umaszczenie jednolite

s – gen warunkuj

ą

cy umaszczenie łaciate

Zadanie:

Jakie b

ę

d

ą

fenotypy potomstwa otrzymanego z kojarze

ń

osobników o genotypach:

a) CCSS x Ccss
b) CcSs x ccSs
c) CcSs x Ccss
d) CCss x CcSs

Zadanie:

Po jakich ró

ż

ni

ą

cych si

ę

umaszczeniem rodzicach mo

ż

e pochodzi

ć

czerwone łaciate ciel

ę

? Poda

ć

genotypy rodziców

DZIEDZICZENIE – PRZEKAZYWANIE CECH
Z POKOLENIA NA POKOLENIE

Dziedziczenie dwóch cech niezale

ż

nych o

dominowaniu

niekompletnym

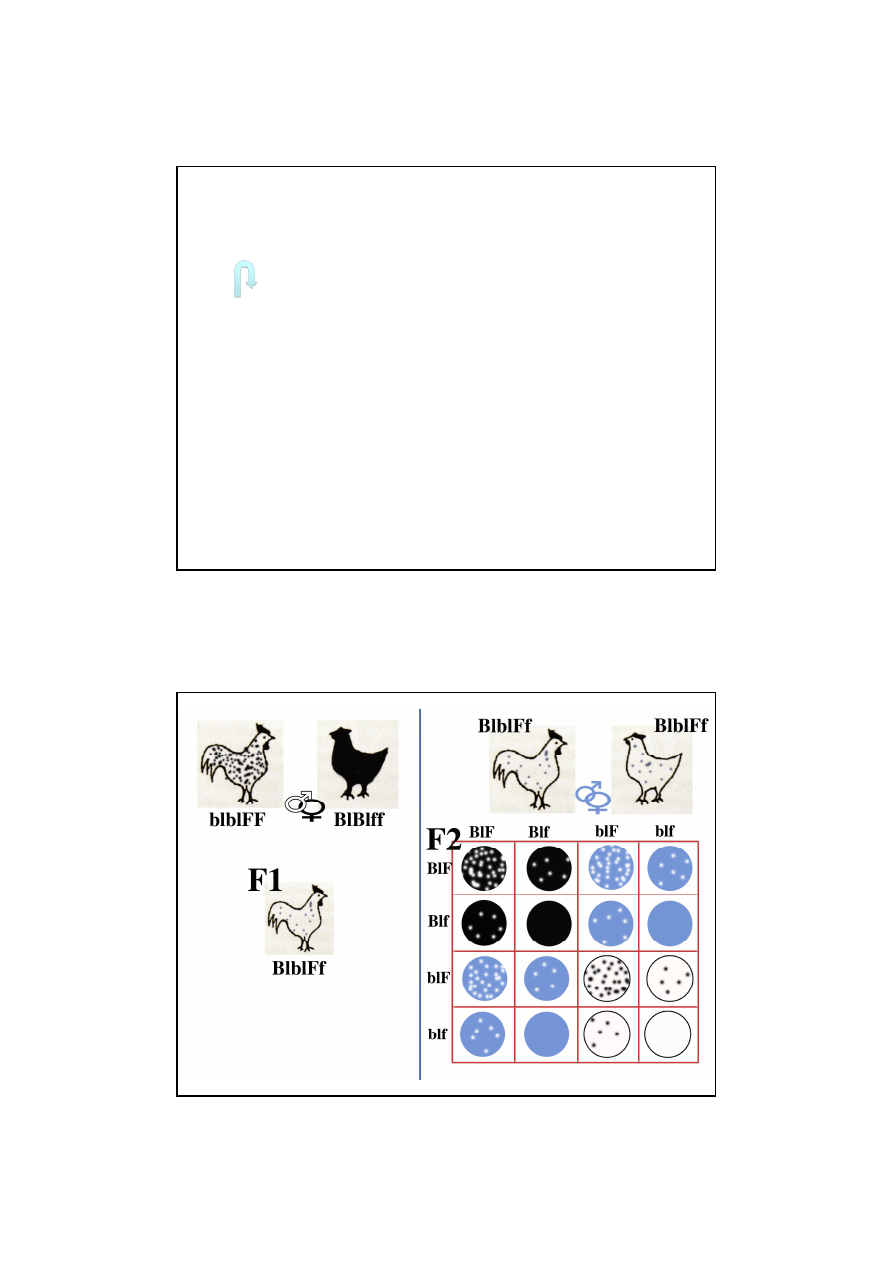
Przykład: dziedziczenie u kur rasy andaluzyjskiej ubarwienie i sposób
upierzenia
Bl – gen warunkuj

ą

cy ubarwienie czarne

– tylko w przypadku homozygoty dominuj

ą

cej (BlBl)

bl – gen warunkuj

ą

cy ubarwienie białe

– tylko w przypadku homozygoty recesywnej (blbl)

W przypadku heterozygoty cecha w fenotypie przyjmuje warto

ś

ci

po

ś

rednie – ubarwienie jest niebieskie (Blbl)

F – gen warunkuj

ą

cy upierzenie szurpate

- tylko w przypadku homozygoty dominuj

ą

cej (FF)

f – gen warunkuj

ą

cy upierzenie gładkie

– tylko w przypadku homozygoty recesywnej (ff)

W przypadku heterozygoty cecha w fenotypie przyjmuje warto

ś

ci

po

ś

rednie – upierzenie jest słabo szurpate (Ff)

Dziedziczenie 2 cech o ró

ż

nym

typie dominowania

Pisum: brak rogów (P) rogato

ść

(p)

Zea: barwa sier

ś

ci czerwona (BB), biała (bb) lub

dereszowata (Bb)

Rodzice: BBpp x bbPP

Gamety: Bp i bP

F1: BbPp

Gamety: BP, Bp, bP, bp

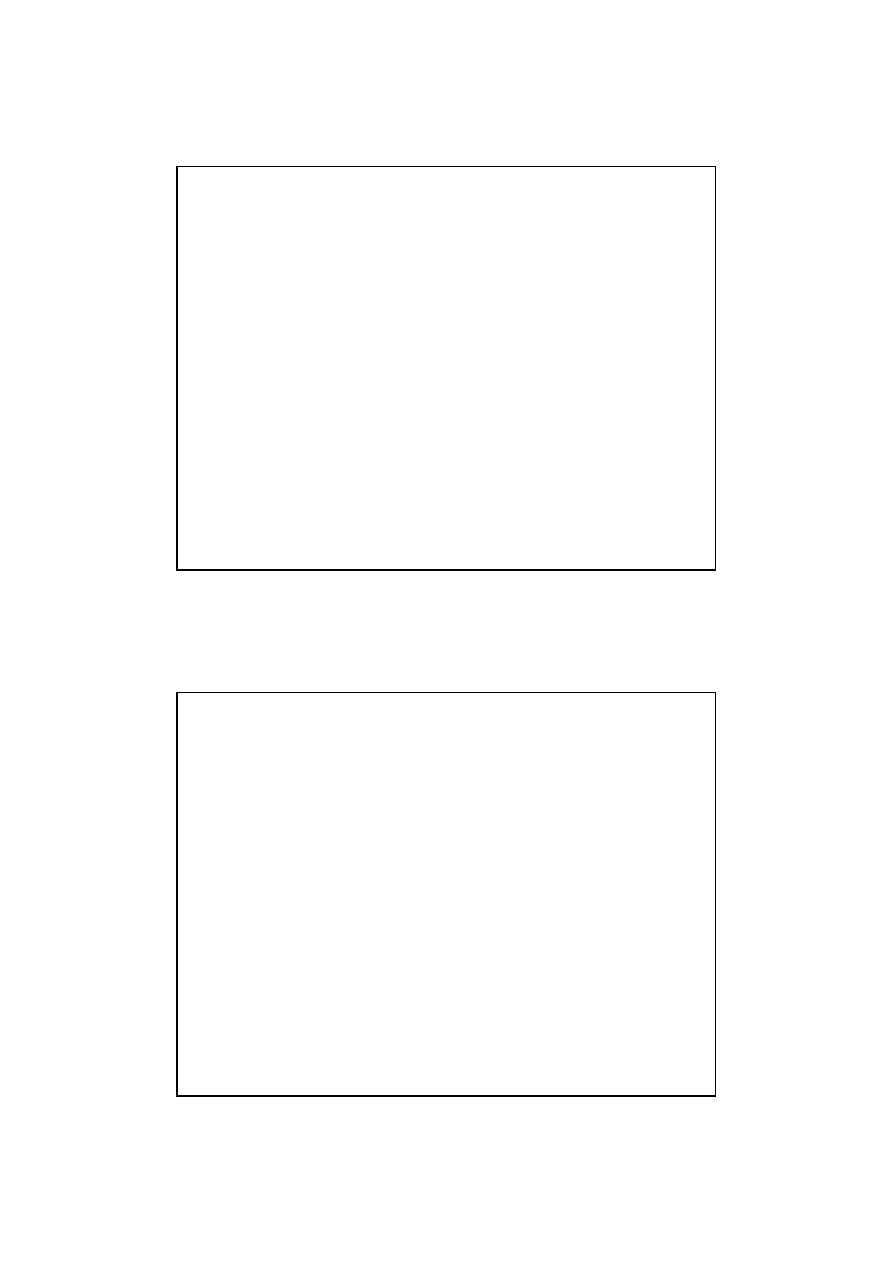
F2:

2 cechy (Zea i Pisum)

Pokolenie F2

bbpp

bbPp

Bbpp

BbPp

bp

bbPp

bbPP

BbPb

BbPP

bP

Bbpp

BbPp

BBpp

BBPp

Bp

BbPp

BbPP

BBPp

BBPP

BP

bp

bP

Bp

BP

gamety

Genotypy: 1:2:1:2:4:2:1:2:1
Fenotypy: 3:1:6:2:3:1

czerwone bez rogów : czerwone z rogami : dereszowate bez rogów : dereszowate z
rogami : białe bez rogów : białe z rogami

Wi

ę

cej cech

Przy rozpatrywaniu rozszczepienia cech stosuje si

ę

prawo

statystyki matematycznej:

Je

ś

li jakie

ś

przypadki zachodz

ą

niezale

ż

nie od siebie, to

prawdopodobie

ń

stwo ich jednoczesnego zaj

ś

cia równe jest

iloczynowi prawdopodobie

ń

stw zaj

ś

cia ka

ż

dego z nich

Prawdopodobie

ń

stwo wyst

ą

pienia fenotypu w F2 dla 2 cech typu PISUM:

sier

ść

czarna - ¾

sier

ść

czerwona - ¼

jednoma

ś

cisto

ść

– ¾

łaciato

ść

– ¼

Czyli czarny, jednoma

ś

cisty – ¾ * ¾ = 9/16

Czarny, łaciaty – ¾ * ¼ = 3/16

2 cechy typu Zea

Cechy kury:
BlBl – pióra czarne
blbl – pióra białe
Blbl – pióra niebieskie

FF – pióra szurpate
ff – pióra proste
Ff – słabo szurpate

Rozpatrujemy ka

ż

d

ą

z cech osobno, by wyznaczy

ć

prawdopodobie

ń

stwo jej

wyst

ą

pienia

Dla 2 pokolenia wywodz

ą

cego si

ę

od homozygotycznego pokolenia P:

pióra czarne 1/4
pióra białe 1/4
pióra niebieskie 2/4

Pióra niebieskie, słabo szurpate - 2/4 * 2/4 = 4/16

Test chi

2

Jak sprawdzi

ć

czy cecha dziedziczy si

ę

zgonie z prawami Mendla,

gdy wyniki eksperymentu nie s

ą

„idealne”.

Eksperyment 1.
Po skrzy

ż

owaniu osobników heterozygotycznych Aa x Aa otrzymali

ś

my

¼ AA - 1000 osobników ma

ś

ci czarnej

¼ aa - 1000 osobników ma

ś

ci białej

½ Aa – 2000 oobników ma

ś

ci czarnej

PROSTE! – dziedziczenie 1
cechy typu Pisum , rozkład
3:1

Eksperyment 2.
Po skrzy

ż

owaniu osobników heterozygotycznych Aa x Aa otrzymali

ś

my

- 32 osobników ma

ś

ci czarnej

- 8 osobników ma

ś

ci białej

?

Test chi2

Słu

ż

y:

-sprawdzeniu zgodno

ś

ci wyników krzy

ż

owa

ń

z zało

ż

onym modelem teoretycznym,

-porównaniu populacji,
-okre

ś

laniu heterozygotyczno

ś

ci potomstwa miesza

ń

cowego

Obliczanie testu X^2:
1. Przygotuj nast

ę

puj

ą

c

ą

tabel

ę

5) d^2/e

4) d^2

Liczba białych - e

Liczba czarnych - e

3) Odchylenie

Teoretyczna l. białych

Teoretyczna l. czarnych

2) Oczekiwana (e)

Liczba białych

Liczba czarnych

1) Obserwowana

Cecha fenotypowa 2

Cecha fenotypowa 1

Cz

ę

stotliwo

ść

2. Zsumuj liczby z rz

ę

du 5) – to da warto

ść

X^2

3. Oblicz liczb

ę

stopni swobody v = n – 1, gdzie n oznacza liczb

ę

klas

potomstwa

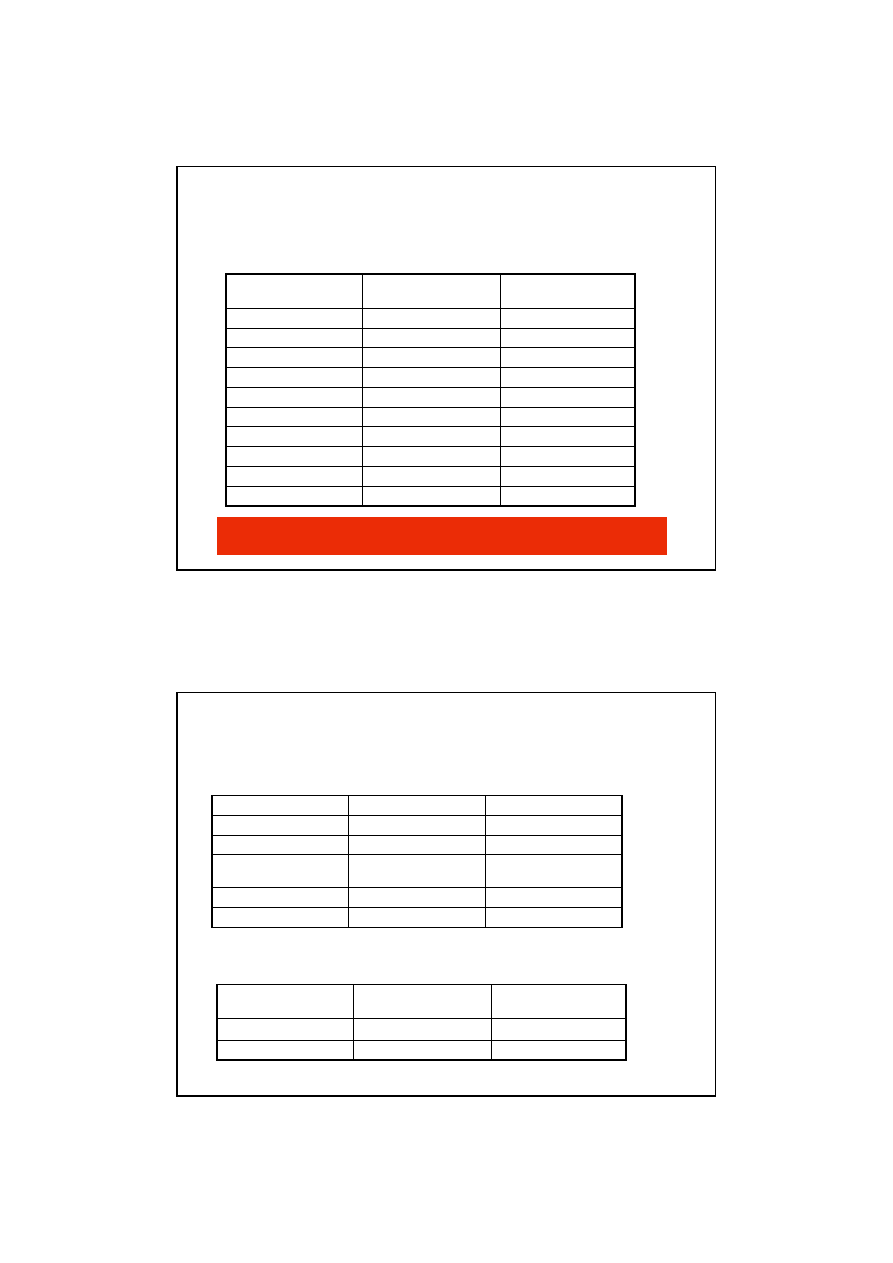
Test chi2

23,21

18,31

10

18,48

14,07

7

16,81

12,59

6

20,09

15,51

8

15,09

11,07

5

21,67

16,92

9

13,28

9,49

4

11,35

7,82

3

9,21

5,99

2

6,64

3,84

1

P=0,01

P=0,05

Liczba stopni
swobody

4. Odczytaj warto

ść

graniczn

ą

z tabeli warto

ś

ci chi^2 dla p=0,05:

Je

ś

li obliczona warto

ść

chi^2 jest mniejsza od warto

ś

ci odczytanej z

tabeli, to wyniki s

ą

zgodne z zało

ż

onym modelem dziedziczenia

Eksperyment 2.
Po skrzy

ż

owaniu osobników heterozygotycznych Aa x Aa otrzymali

ś

my

¼ AA - 32 osobników ma

ś

ci czarnej

¼ aa - 8 osobników ma

ś

ci białej

0,4

0,133

5) d^2/e

4

4

4) d^2

8 – 10 = -2

32 - 30 = 2

3) Odchylenie

¼ * 40 = 10

¾ * 40 = 30

2) Oczekiwana (e)

8

32

1) Obserwowana

Ma

ść

biała

Ma

ść

czarna

Cz

ę

stotliwo

ść

X^2 = 0,53
v = 2 - 1 = 1

9,21

5,99

2

6,64

3,84

1

Warto

ść

X^2 dla

P=0,01

Warto

ść

X^2 dla

P=0,05

Liczba stopni
swobody

0,53 < 3,84, wi

ę

c przyj

ę

ty model dziedziczenia jest poprawny

Zakładamy dziedziczenie PISUM

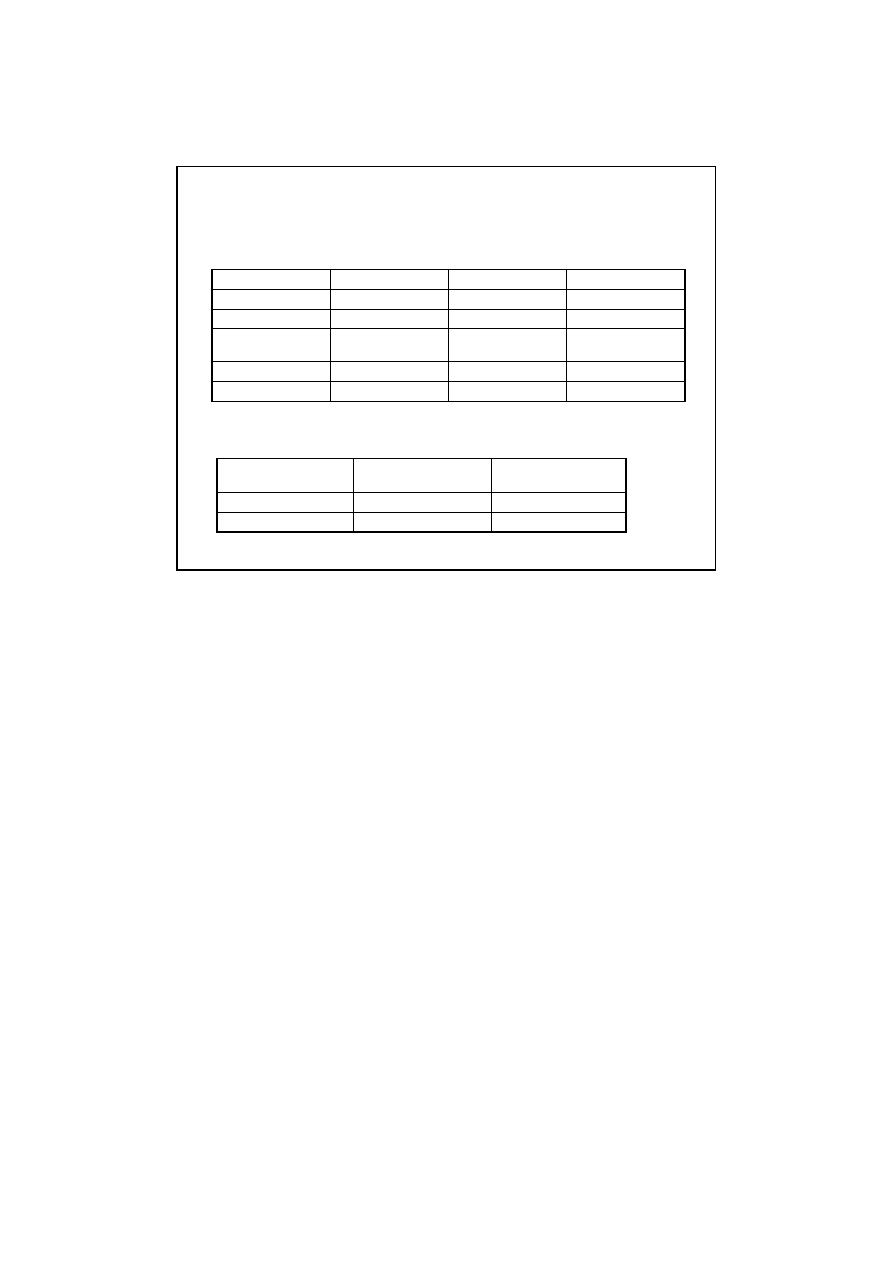
Eksperyment 2.
Po skrzy

ż

owaniu osobników heterozygotycznych Aa x Aa otrzymali

ś

my

¼ AA - 32 osobników ma

ś

ci czarnej

¼ aa - 8 osobników ma

ś

ci białej

0,4

4

8 – 10 = -2

¼ * 40 = 10

8

Ma

ść

biała

2

48,4

5) d^2/e

400

484

4) d^2

0 – 20 = -20

32 - 10 = 22

3) Odchylenie (d)

1/2 * 40 = 20

1/4 * 40 = 10

2) Oczekiwana (e)

0

32

1) Obserwowana

Ma

ść

niebieska

Ma

ść

czarna

Cz

ę

stotliwo

ść

X^2 = 50,8
v = 3 - 1 = 2

9,21

5,99

2

6,64

3,84

1

Warto

ść

X^2 dla

P=0,01

Warto

ść

X^2 dla

P=0,05

Liczba stopni
swobody

50,8 > 5,99, wi

ę

c przyj

ę

ty model dziedziczenia jest bł

ę

dny

Zakładamy dziedziczenie ZEA – pojawiaj

ą

si

ę

3 fenotypy