Mechanika płynów

1

Dr Tomasz Wajman

Zespół Maszyn Wodnych i Mechaniki Płynów

Instytut Maszyn Przepływowych PŁ

E-mail: [e-mail]

Przepływy laminarne

i turbulentne

i turbulentne

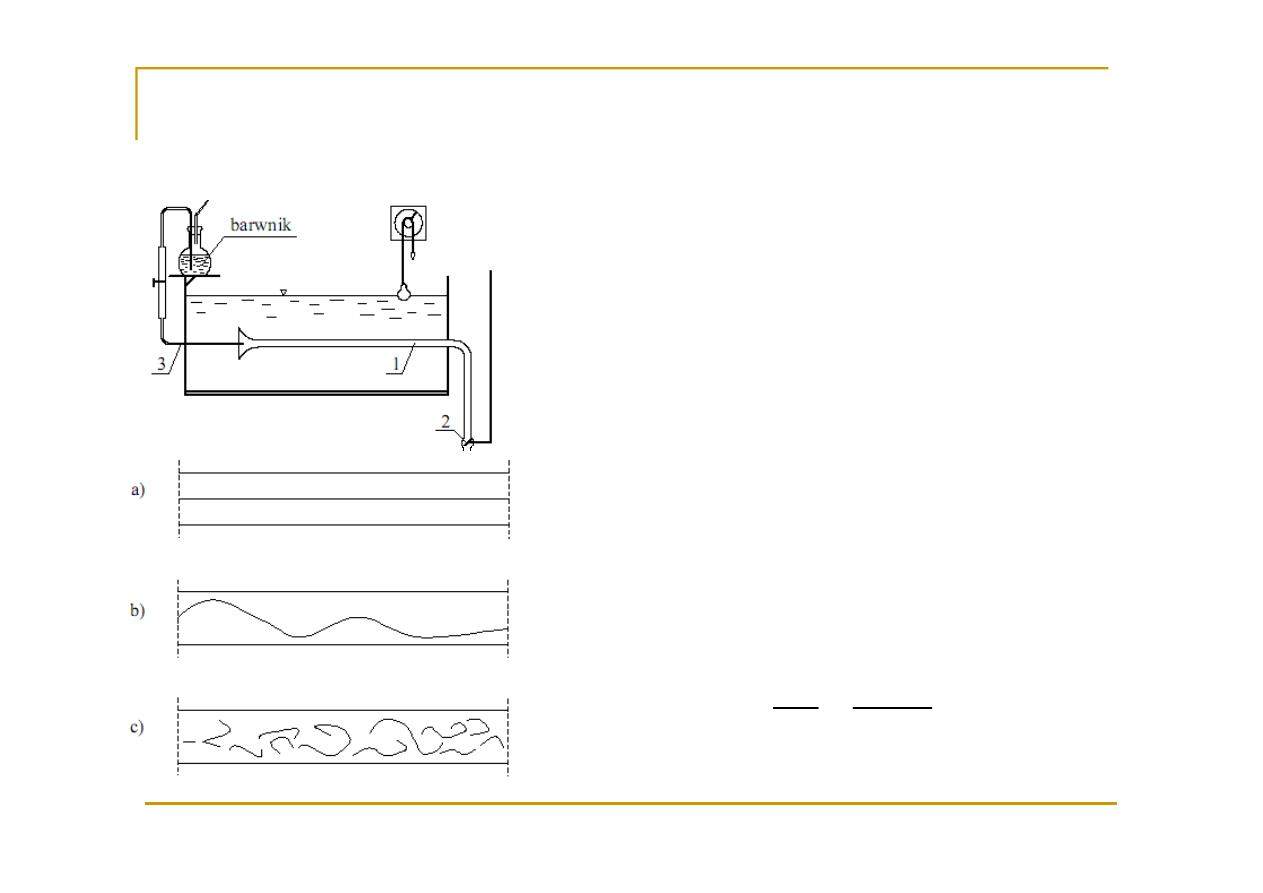
Doświadczenie Reynolds’a

Podział przepływów na dwa rodzaje:

- laminarny przed utratą stateczności (a)

- turbulentny po utracie stateczności (b)

Ruch laminarny tzn. warstwowy, czyli
charakteryzujący się nie mieszaniem poszczególnych
warstw płynu, tylko jak gdyby „ślizganiem się ich po
sobie”.

Ruch turbulentny jest niestacjonarny z bardzo

3

Ruch turbulentny jest niestacjonarny z bardzo
złożonymi torami elementów płynu, mieszający się
nieustannie i nie wykazujący jakiejś widocznej
powtarzalności. Elementy płynu w ruchu turbulentnym
przemieszczają się zgodnie z głównym kierunkiem
transportu masy, wykonując jednocześnie trudne do
przewidzenia ruchy pulsacyjne wzdłuż i w poprzek
głównego kierunku ruchu

idem

µ

ρ

v

l

ν

v

l

=

⋅

⋅

=

⋅

=

Re

Dla Re < 2300 przepływ w rurze kołowej jest zawsze

laminarny, a dla Re > 50000 jest zawsze turbulentny

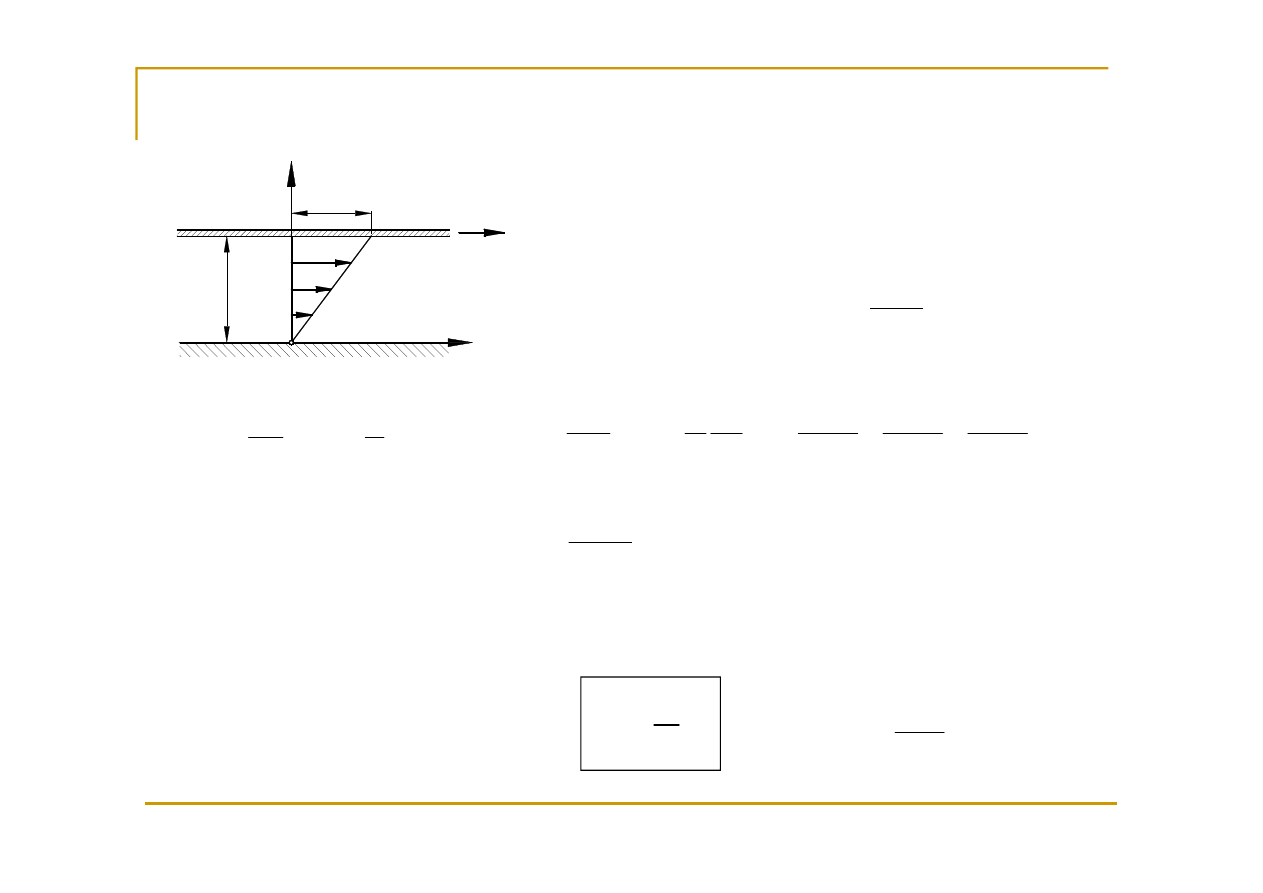
Przepływ Couette’a

x

y

II

I

U

0

s

0

v

v

z

y

=

=

0

)

y

(

v

x

≠

0

x

v

x

=

∂

∂













∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

−

=

2

x

2

2

x

2

2

x

2

x

v

v

v

1

d

dv

z

y

x

x

p

X

t

υ

ρ

Z równania ciągłości

R. N-S

v

p

ρ

F

t

v

m

r

r

r

r

2

1

d

d

∇

+

∇

−

=

υ

dla









∂

∂

∂

∂

2

2

2

d

z

y

x

x

X

t

ρ

0

y

v

2

x

2

=

∂

∂

2

1

C

y

C

v

x

+

=

0

=

y

0

=

x

v

s

y

=

U

v

x

=

U

s

y

v

x

=

1300

Re

,

Re

≤

⋅

=

kr

s

U

υ

R. N-S

v

p

ρ

F

t

m

d

∇

+

∇

−

=

υ

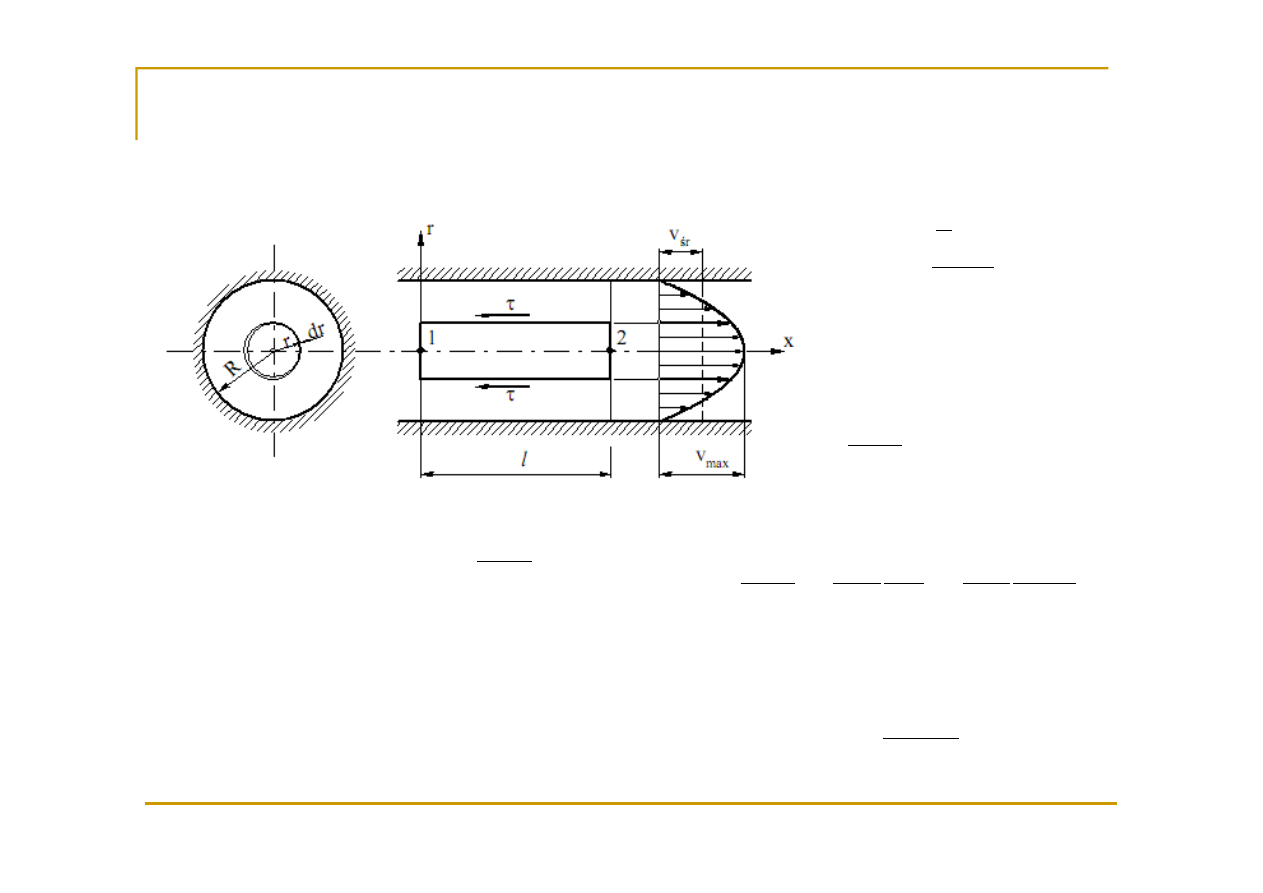
Laminarny przepływ w rurze kołowej

- Przepływ Hagena-Poiseuille’a

0

=

=

r

v

v

ϕ

0

=

∂

∂v

x

2300

Re

≤

⋅

=

υ

d

v

5

x

r

r

v

x

r

d

π

2

d

π

2

x

∂

∂

=

µ

τ

Siły tarcia:

Siły ciśnienia:

p

r

d

2

π

l

p

r

x

p

r

r

v

st

x

2

d

d

2

∆

=

=

∂

∂

µ

µ

0

=

∂

x

R

r

=

0

=

x

v

dla

0

=

r

2

str

max

4

R

l

p

v

x

µ

∆

=

dla

Laminarny przepływ w rurze kołowej

- Przepływ Hagena-Poiseuille’a

2

st

max

8

2

1

R

l

p

v

v

x

µ

∆

=

=

(

)

2

2

st

4

r

R

l

p

v

x

−

∆

=

µ

max

2

1

x

v

v

=

6

8

2

l

µ

d

l

v

p

2

Re

64

2

st

ρ

=

∆

d

l

v

d

v

d

v

l

R

v

l

p

2

64

2

3

8

2

2

2

st

ρ

υ

µ

µ

=

=

=

∆

d

l

v

f

p

2

2

T

st

ρ

=

∆

Re

64

T

=

f

Turbulentny przepływ w rurze kołowej













=

k

d

f

f

Re,

T

T

3164

,

0

d

l

v

f

p

2

2

T

st

ρ

=

∆

7

dla przepływu turbulentnego (dla rur gładkich k = 0) wg Blasiusa

( )

4

/

1

T

Re

3164

,

0

=

f

dla przepływu turbulentnego (dla rur chropowatych) - wykres Nikuradse

ś

rednica zast

ę

pcza dla rur

o niekołowym przekroju

S

A

d

z

4

=

A

– pole przekroju

S

– obwód zwilżony

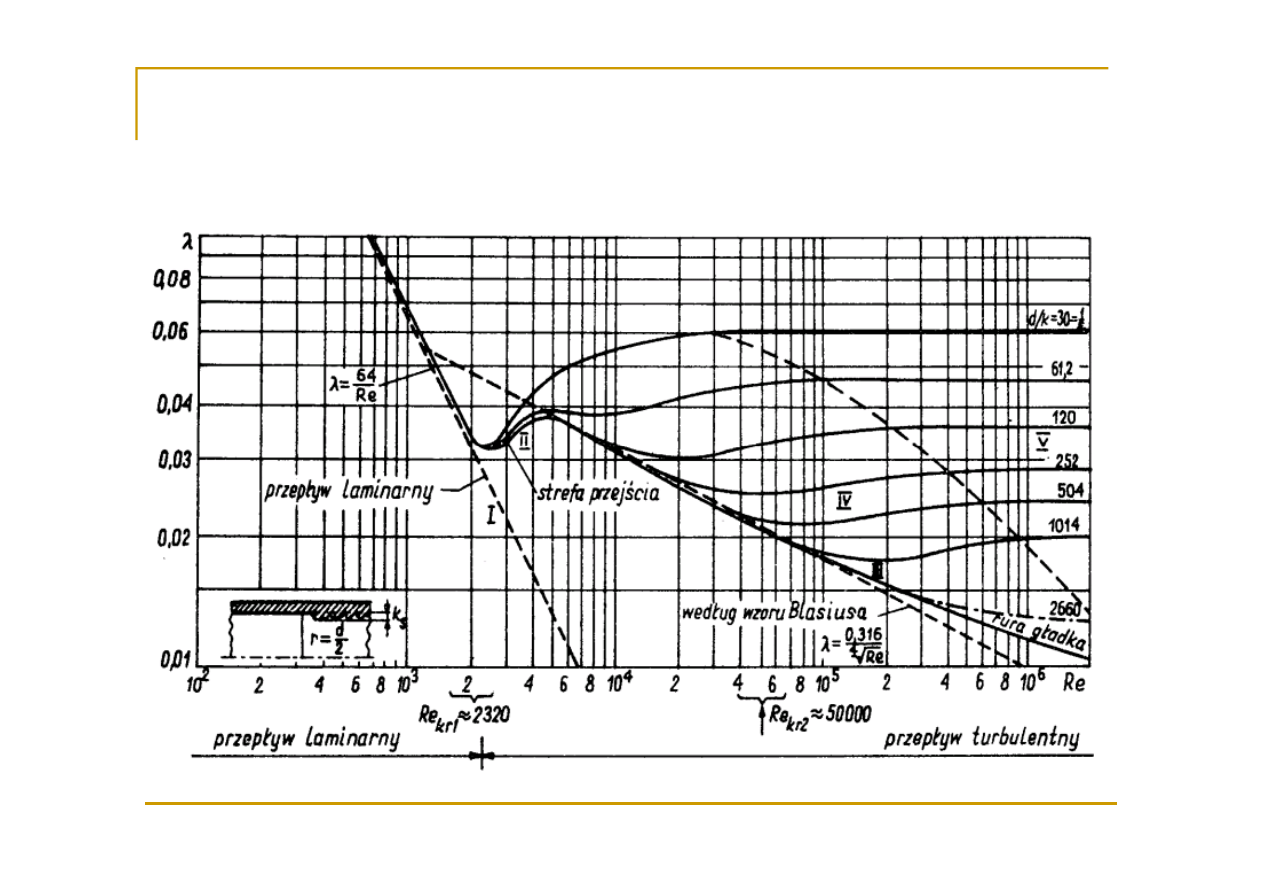
Współczynnik strat tarcia

– wykres Nikuradse

8

Półempiryczne równanie Bernoulliego

2

1

str

2

2

2

2

1

1

2

1

2

2

-

p

z

g

ρ

p

ρv

z

g

ρ

p

ρv

∆

+

+

+

=

+

+

9

d

l

v

k

d

f

p

2

Re,

2

T

st

ρ













=

∆

(

)

2

geom.

Re

ζ

2

sm

v

,

p

ρ

=

∆

Straty liniowe - tarcia

Straty miejscowe