
Mechanika Płynów
Dr Tomasz Wajman
Zespół Maszyn Wodnych i Mechaniki Płynów
Instytut Maszyn Przepływowych PŁ
Pokój 110, tel. 42 631 23 60, (24 54)
E-mail: tomasz.wajman@p.lodz.pl

Literatura
• Zbyszko Kazimierski, „Podstawy mechaniki płynów i metod
komputerowej symulacji przepływów”, Łódź, 2004.
• Zbyszko Kazimierski, Zdzisław Orzechowski, „Laboratorium
z mechaniki płynów”, Łódź, 2001.
• Zdzisław
Orzechowski,
Paweł
Wewiórski,
„Ćwiczenia
• Zdzisław
Orzechowski,
Paweł
Wewiórski,
„Ćwiczenia
audytoryjne z mechaniki płynów”, Łódź, 1999.
• Zbyszko Kazimierski, Zdzisław Orzechowski, „Mechanika
płynów”, Łódź, 1986.

Płyny
Płyny – ciała posiadające zdolność do zmiany swych kształtów
pod działaniem dowolnie małych sił zewnętrznych, jeśli działają
one dostatecznie długo.
Płyny - różnią się od ciał stałych tym, że nie posiadają tzw.
Płyny - różnią się od ciał stałych tym, że nie posiadają tzw.
sztywności postaciowej. Wynika to z ich struktury cząsteczkowej
i małych wewnętrznych sił spójności w porównaniu z ciałami
stałymi.
Płyny dzielimy na ciecze i gazy.

Płyny – ciecze i gazy
Ciecze - płyny, które zmieniają nieznacznie swoją objętość pod
działaniem sił zewnętrznych (nawet bardzo dużych) -
ciecze są
nieściśliwe
.
Wypełniają część zbiorników, równą objętości wprowadzonej
cieczy, tworzą powierzchnie swobodne, oraz krople w wyniku
działania napięcia powierzchniowego.
działania napięcia powierzchniowego.
Gazy - płyny, które zmieniają łatwo swą objętość pod działaniem
zewnętrznych sił –
duża ściśliwość
.
Wypełniają całe objętości naczyń, w których się znajdują.
Procesy sprężania i rozprężania gazów podlegają znanym
przemianom termodynamicznym.
Mechanika Płynów
• Zjawiska występujące podczas ruchu i spoczynku płynów wraz
z oddziaływaniem płynów na ścianki ciał stałych zanurzonych
w płynie.
• Poznanie praw rządzących ruchem płynów (szczególnie
przepływów turbulentnych).
przepływów turbulentnych).
Mechanika Płynów
Statyka
Kinematyka Dynamika
Ruch ↔ siły
Ruch
Płyn nieruchomy
względem naczynia

Ośrodek ciągły. Element płynu.
Ośrodek ciągły - płyn wypełnia przestrzeń w sposób ciągły,
bez pustych obszarów typowych dla struktury molekularnej
i związanych z tym zjawisk mikroskopowych.
Sformułowane zostaną prawa makro-mechaniki w odniesieniu
do tzw. elementu płynu. Element płynu dV jest to bardzo
mała ilość płynu, której wymiary liniowe są dużo mniejsze
mała ilość płynu, której wymiary liniowe są dużo mniejsze
od wymiarów opływanych ciał lub kanałów, a jednocześnie
o wymiarach dużo większych od średniej drogi swobodnej
molekuł lub ich temperaturowej amplitudy drgań.
Elementy płynu zawierają ogromną liczbę molekuł.
(1
µm
3
powietrza zawiera w warunkach normalnych około 27mln molekuł)

Zasady zachowania
Model ośrodka ciągłego pozwala na określenie
makroskopowych własności płynu jako funkcji przestrzeni
oraz czasu i potraktowanie ich jako pól, co stwarza
możliwości zastosowania ogólnych twierdzeń teorii pola
w mechanice płynów.
Prawa rządzące zachowaniem się płynów zostaną
sformułowane w oparciu o podstawowe zasady fizyki tj.:
• zasadę zachowania masy,
• zasadę zachowania pędu i momentu pędu (krętu),
• zasadę zachowania energii.

Parametry termodynamiczne
i kinematyczne
Podstawowymi parametrami termodynamicznymi są:
• gęstość
• ciśnienie p,
• temperatura bezwzględna T,
• energia wewnętrzna u,
,
ρ
• energia wewn
ę
trzna
u
,
• entalpia
h
.
dla cieczy
dla gazów idealnych:
Podstawowy parametr kinematyczny:
prędkość
v
r
const.
=
ρ
T
c
h
T
c
u
RT
p
p
v
=
=
=
,
,
ρ

Własności dyssypatywne płynów
Podczas ruchu płynów w układach adiabatycznych, energia
mechaniczna płynu zmniejsza si
ę
przechodz
ą
c w energi
ę
ciepln
ą
(w sposób nieodwracalny).
Proces taki nazywamy
dyssypacją
(rozpraszaniem) energii
mechanicznej.
mechanicznej.
Procesy dyssypacji s
ą
zwi
ą
zane z takimi makroskopowymi
własno
ś
ciami płynu jak:
•
lepkość
, która powoduje zjawiska tarcia (napr
ęż
enia
styczne),
•
przewodnością cieplną
, która powoduje przepływ energii
z obszarów o wy
ż
szej temperaturze do obszarów
o temperaturze ni
ż
szej.

Statyka cieczy

Statyka cieczy
Statyka cieczy
zajmuje si
ę
zagadnieniami równowagi cieczy,
a tak
ż
e obliczaniem sił wywieranych przez nieruchom
ą
ciecz na
ś
ciany zbiorników oraz na ciała nieruchome w niej zanurzone.
Równowaga ta mo
ż
e mie
ć
charakter bezwzgl
ę
dny lub wzgl
ę
dny.
W obu przypadkach elementy cieczy nie zmieniaj
ą
swego
poło
ż
enia wzgl
ę
dem siebie i
ś
cian naczynia, lecz w przypadku
równowagi bezwzgl
ę
dnej ciecz jest nieruchoma wzgl
ę
dem
ziemi, a w przypadku równowagi wzgl
ę
dnej ciecz wraz
z naczyniem znajduje si
ę
w ruchu.
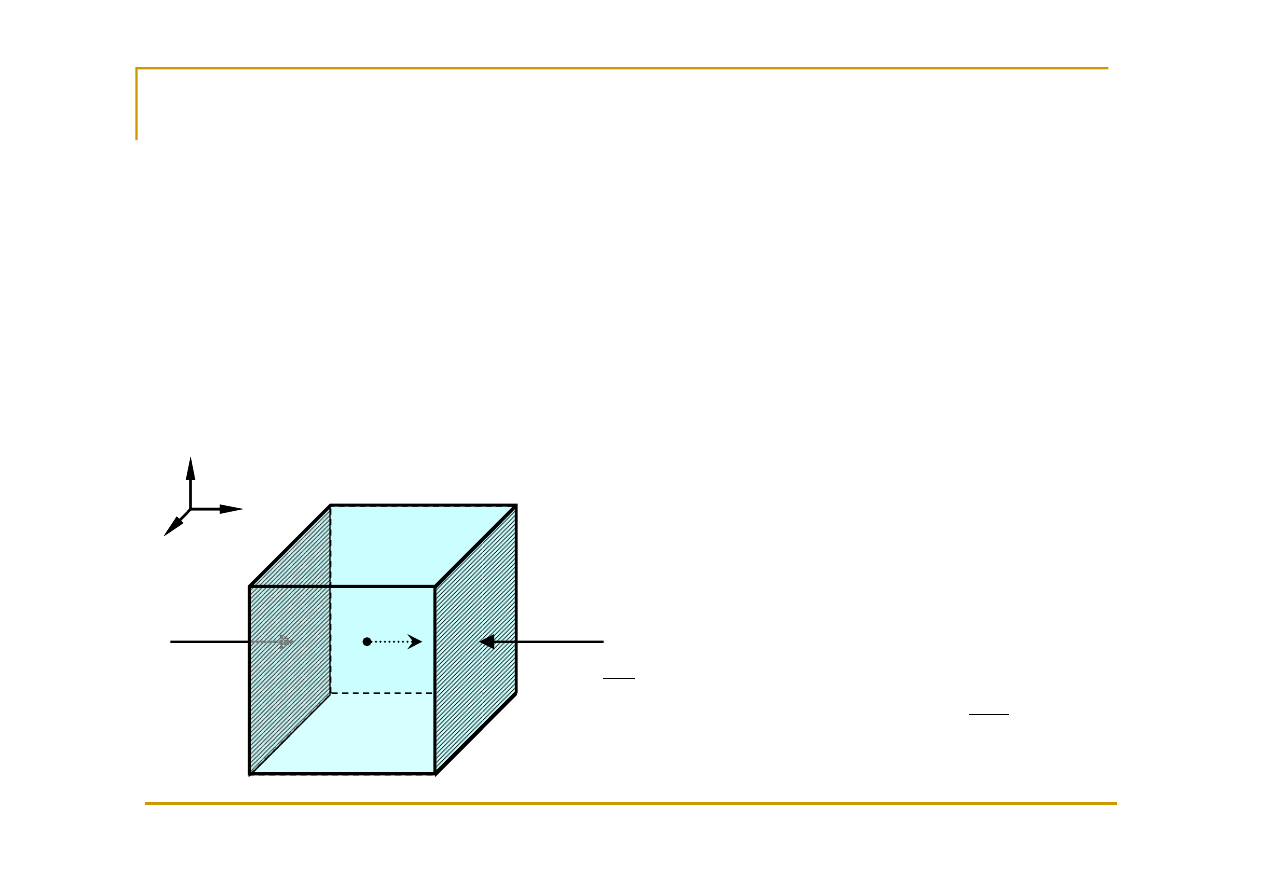
Równanie równowagi
z
y
x
V
d
d
d
d
=
Element płynu b
ę
d
ą
cy w spoczynku musi znajdowa
ć
si
ę
pod
działaniem całkowicie równowa
żą
cych si
ę
sił.
Równowaga musi zaistnie
ć
mi
ę
dzy siłami powierzchniowymi
i siłami masowymi.
Y j
r
Y j
r
x
x
p
p
x
x
p
d
)
d
(
∂
∂
+
=
+
)
(x
f
p
=
X
Y
Z
i
r
j
r
k
r
X
Y
Z
i
r
j
r
k
r
x
x
p
p
d
∂
∂
+
y
d
x
d
z
d
p
x
F
r
Siły powierzchniowe
Rozwa
ż
amy składow
ą
X

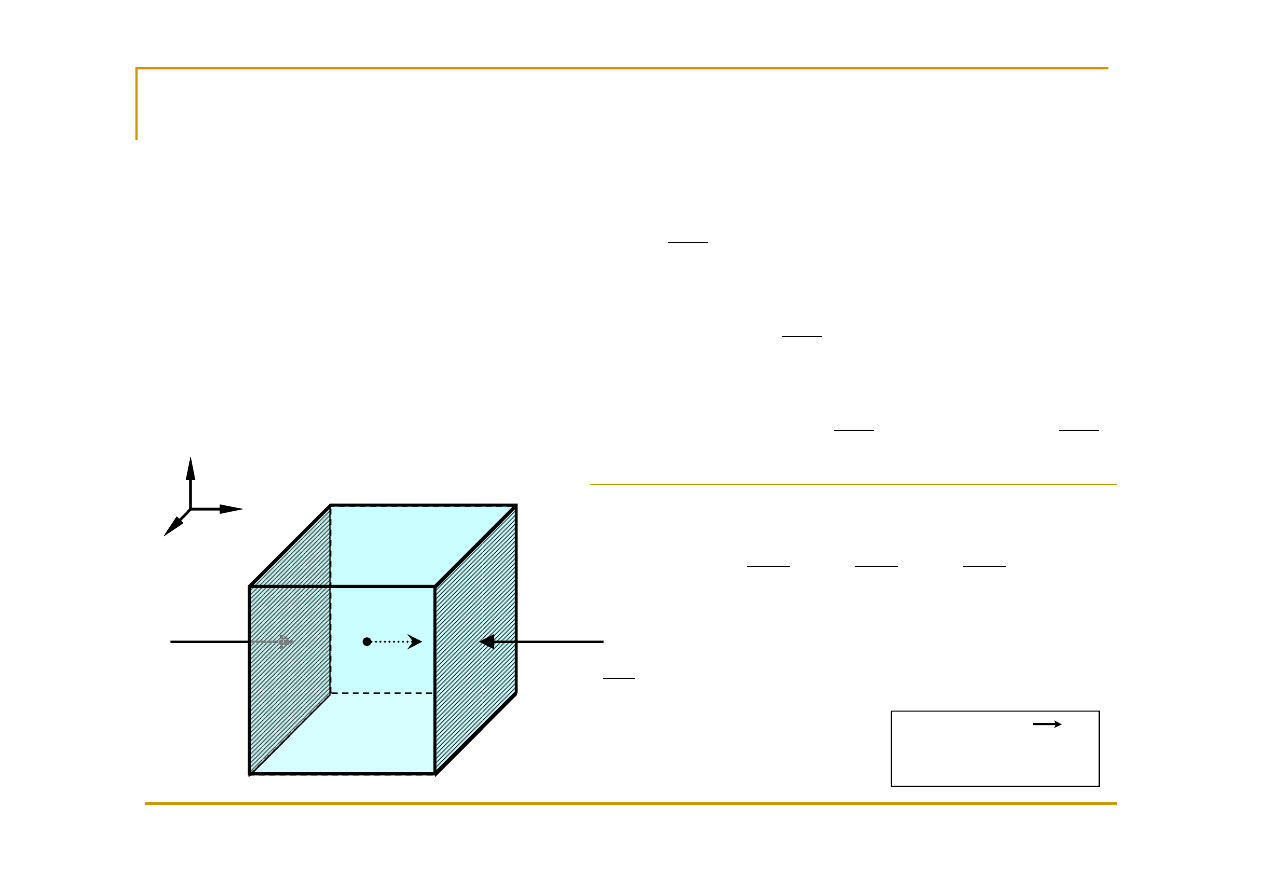
Równanie równowagi
Siła masowa – siła, której warto
ść
jest proporcjonalna do
masy ciała na które działa:
z
y
x
X
V
X
m
X
F
x
d
d
d
d
d
ρ
ρ
=
=
=
Y j
r
Y j
r
x
x
F
i
F
r
r
=
V
m
d
d
ρ
=
z
y
x
V
d
d
d
d
=
X
Y
Z
i
r
j
r
k
r
X
Y
Z
i
r
j
r
k
r
x
x
p
p
d
∂
∂
+
y
d
x
d
z
d
p
x
F
r
Równanie równowagi
0
d
d
d
d
d
d
d
d
=
+
∂
∂
+
−
z
y
x
X
z
y
x
x
p
p
z
y
p
ρ
x
p
i
X
i
x
p
X
∂
∂
=
⇒
∂
∂
=
r
r
ρ
ρ
0
d
d
d
=
+
∂
∂
−
z
y
x
X
x
p
ρ
z
y
x
X
F
x
d
d
d
ρ
=
Y j
r
Y j
r
p
F
∇
=
m
r
ρ
Z
k
Y
j
X
i
F
r
r
r
r
+
+
=
m
p
z
p
k
y
p
j
x
p
i
∇
=
∂
∂
+
∂
∂
+
∂
∂
r
r
r
r
df
x
i
X
i
x
X
∂
=
⇒
∂
=
ρ
ρ
z
y
x
X
F
x
d
d
d
ρ
=
x
x
p
p
d
∂
∂
+
X
Y
Z
i
r
j
r
k
r
X
Y
Z
i
r
j
r
k
r
y
d
x
d
z
d
p
x
F
r
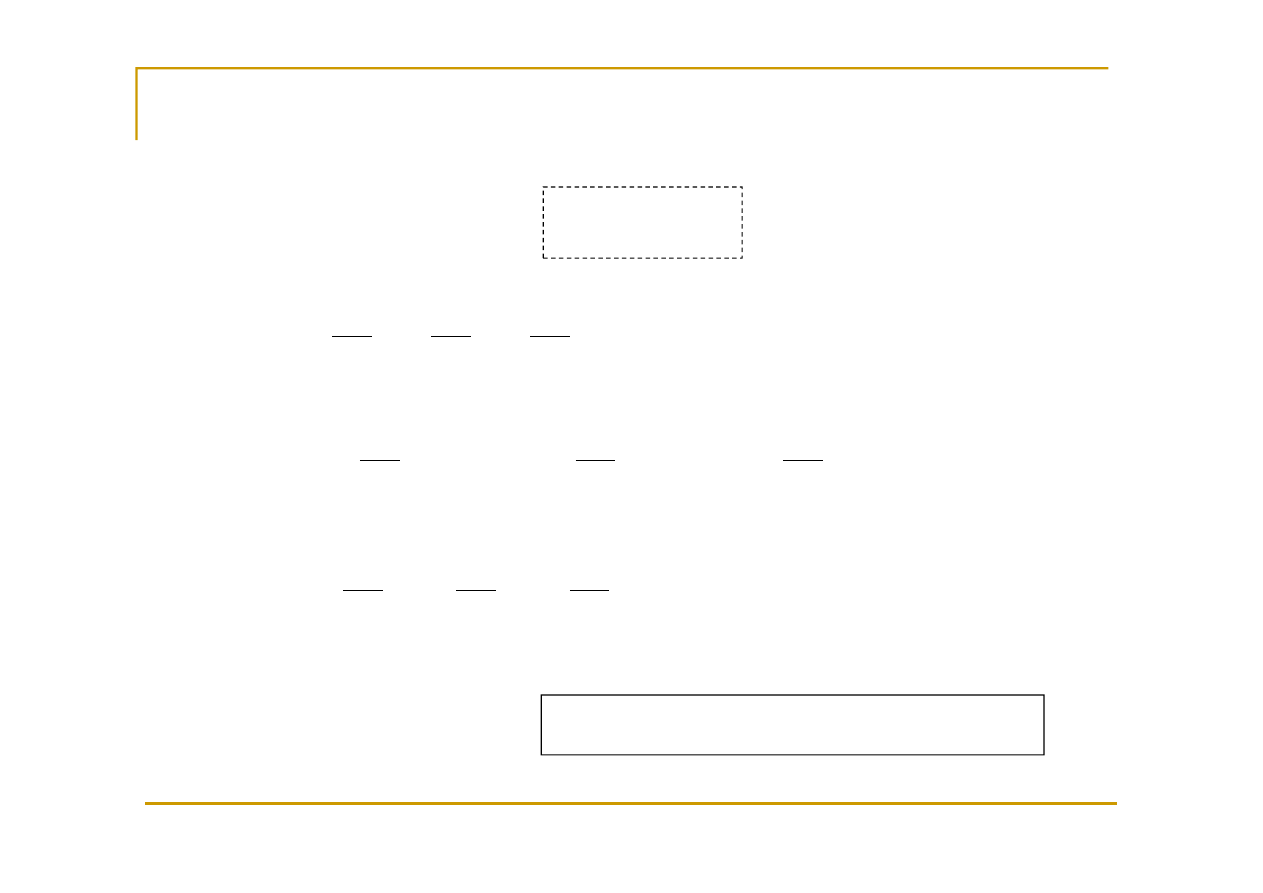
Z
p
Y
p
X
p
ρ
ρ
ρ
=
∂
=
∂
=
∂
,
,
Równanie równowagi
m
F
p
r
r
ρ
=
∇
z
p
k
y
p
j
x
p
i
p
∂
∂
+
∂
∂
+
∂
∂
=
∇
r
r
r
r
Z
k
Y
j
X
i
F
r
r
r
r
+
+
=
m
)
d
d
d
(
d
z
Z
y
Y
x
X
p
+
+
=
ρ
Z
z
p
Y
y
p
X
x
p
ρ
ρ
ρ
=
∂
∂
=
∂
∂
=
∂
∂
,
,
(
)
z
Z
y
Y
x
X
z
z
p
y
y
p
x
x
p
d
d
d
d
d
d
+
+
=
∂
∂
+
∂
∂
+
∂
∂
ρ
Ró
ż
niczka ci
ś
nienia
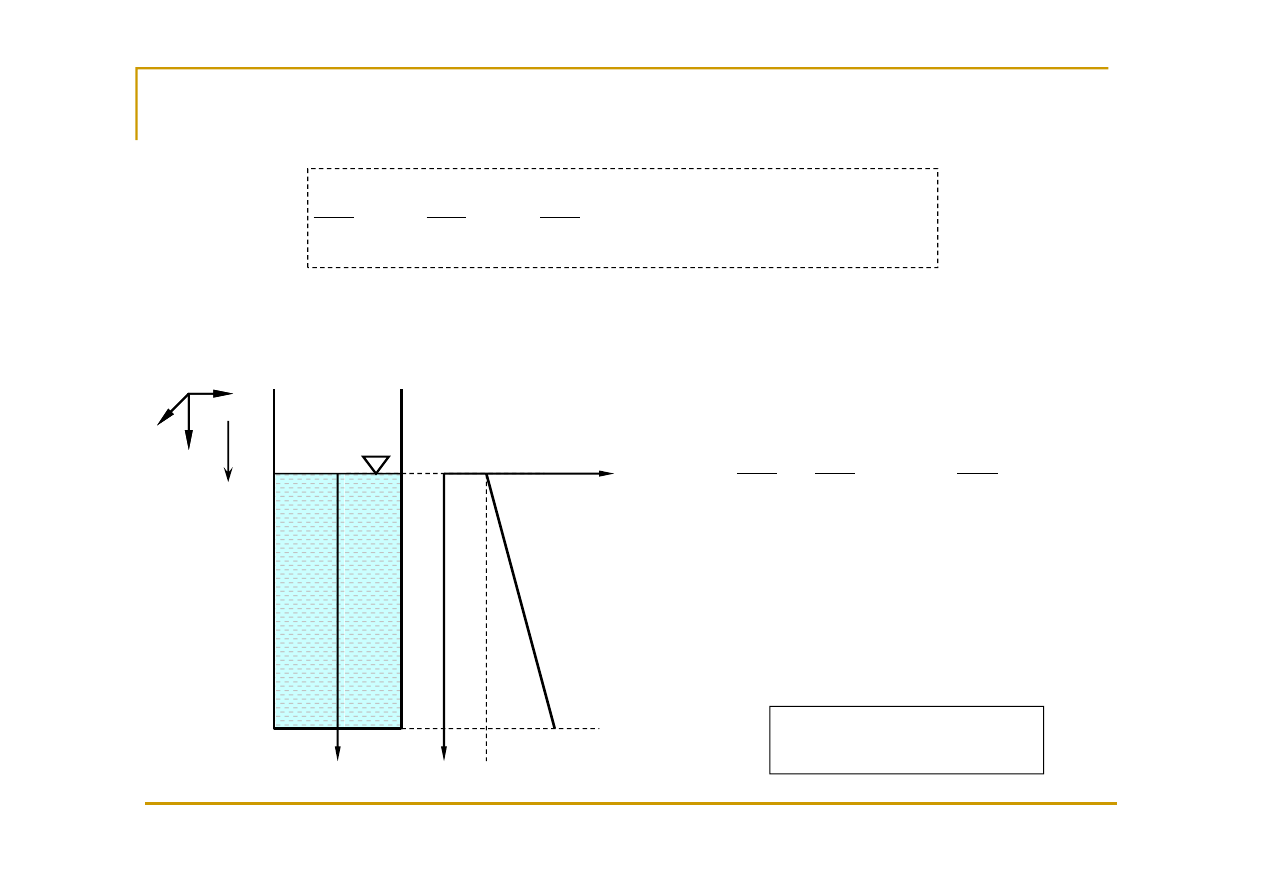
Najczęściej spotykanym polem sił masowych w zagadnieniach równowagi cieczy jest pole
grawitacji ziemskiej.
g
Z
0,
Y
,
0
=
=
=
X
p
p
p
ρ
=
=
∂
=
∂
d
Równanie manometryczne
(
)
z
Z
y
Y
x
X
z
z
p
y
y
p
x
x
p
d
d
d
d
d
d
+
+
=
∂
∂
+
∂
∂
+
∂
∂
ρ
a
p
X
Y
Z
X
Y
Z
g
r
p
p
g
z
p
y
p
x
p
ρ
=
=
∂
∂
=
∂
∂
d
d
,
0
z
g
p
p
ρ
+
=
a
a
a
C
0,
z
dla
p
p
p
=
⇒
=
=
C
z
g
p
+
=
ρ
a
Z
Z
g
z
z
p
a
p
H
g
p
a
ρ
+
H

Równowaga względna cieczy
Gdy w poruszaj
ą
cym si
ę
naczyniu z ciecz
ą
elementy cieczy s
ą
nieruchome wzgl
ę
dem siebie i
ś
cianek naczynia mo
ż
emy
stosowa
ć
równania równowagi cieczy uzupełniaj
ą
c siły masowe
o nowy rodzaj tych sił zwi
ą
zany z ruchem naczynia.
Wykorzystamy to w dwóch przypadkach:
• post
ę
powego, jednostajnie przyspieszonego ruchu
naczynia,
• ruchu obrotowego.
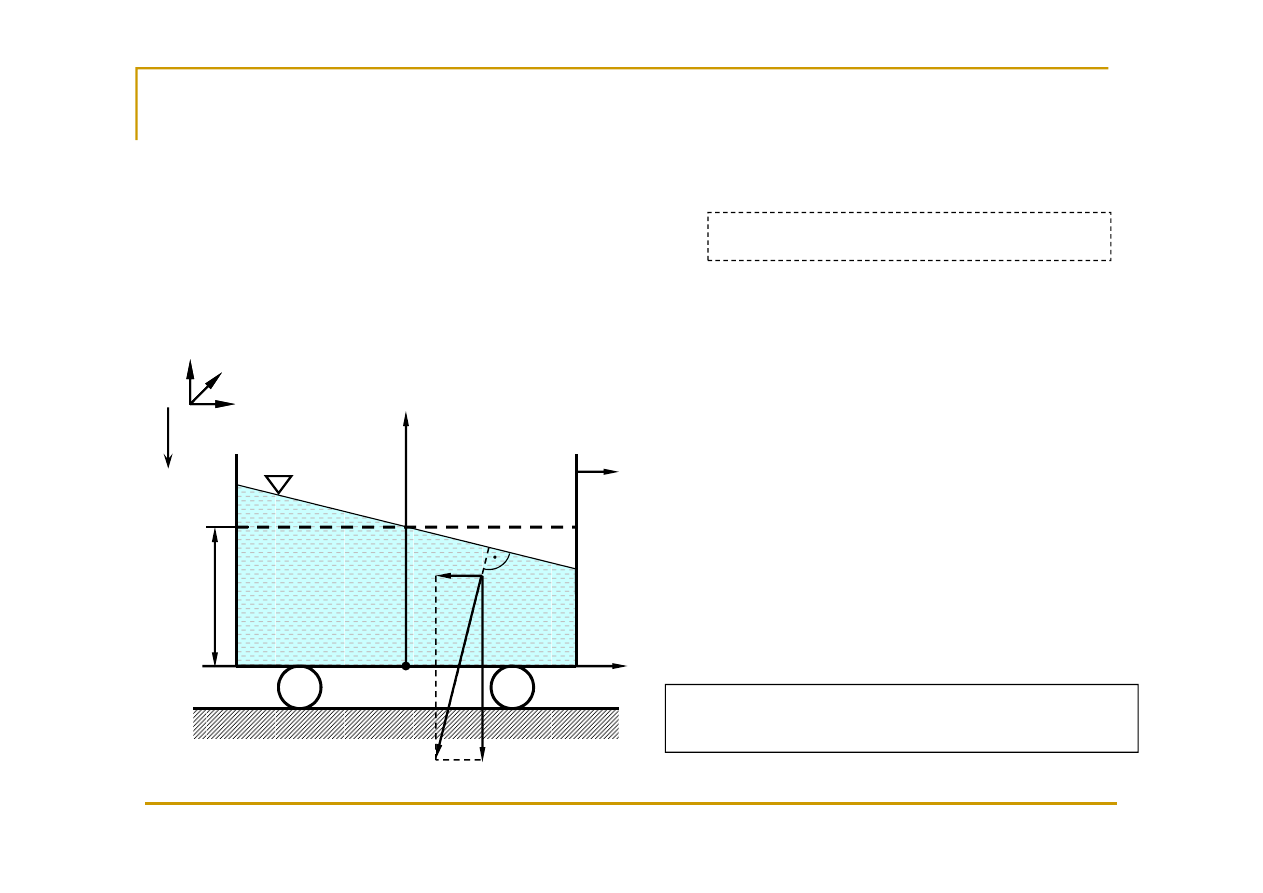
Postępowy ruch naczynia
)
d
d
d
(
d
z
Z
y
Y
x
X
p
+
+
=
ρ
g
, Z
a, Y
X
−
=
=
−
=
0
)
d
d
(
d
z
g
x
a
p
+
−
=
ρ
C
z
g
x
a
p
+
+
−
=
)
(
ρ
X
Y
Z
X
Y
Z
g
r
p
z
a
r
Wyznaczenie warto
ś
ci
ci
ś
nienia
C
z
g
x
a
p
+
+
−
=
)
(
ρ
1
1
0
dla
z
g
ρ
p
C
p
p
,
z
z
,
x
a
a
+
=
=
=
=
(
)
[
]
ax
z
z
g
p
p
−
−
+
=
1
a
ρ
a
p
x
a
r
1
z
a
r
−
g
r
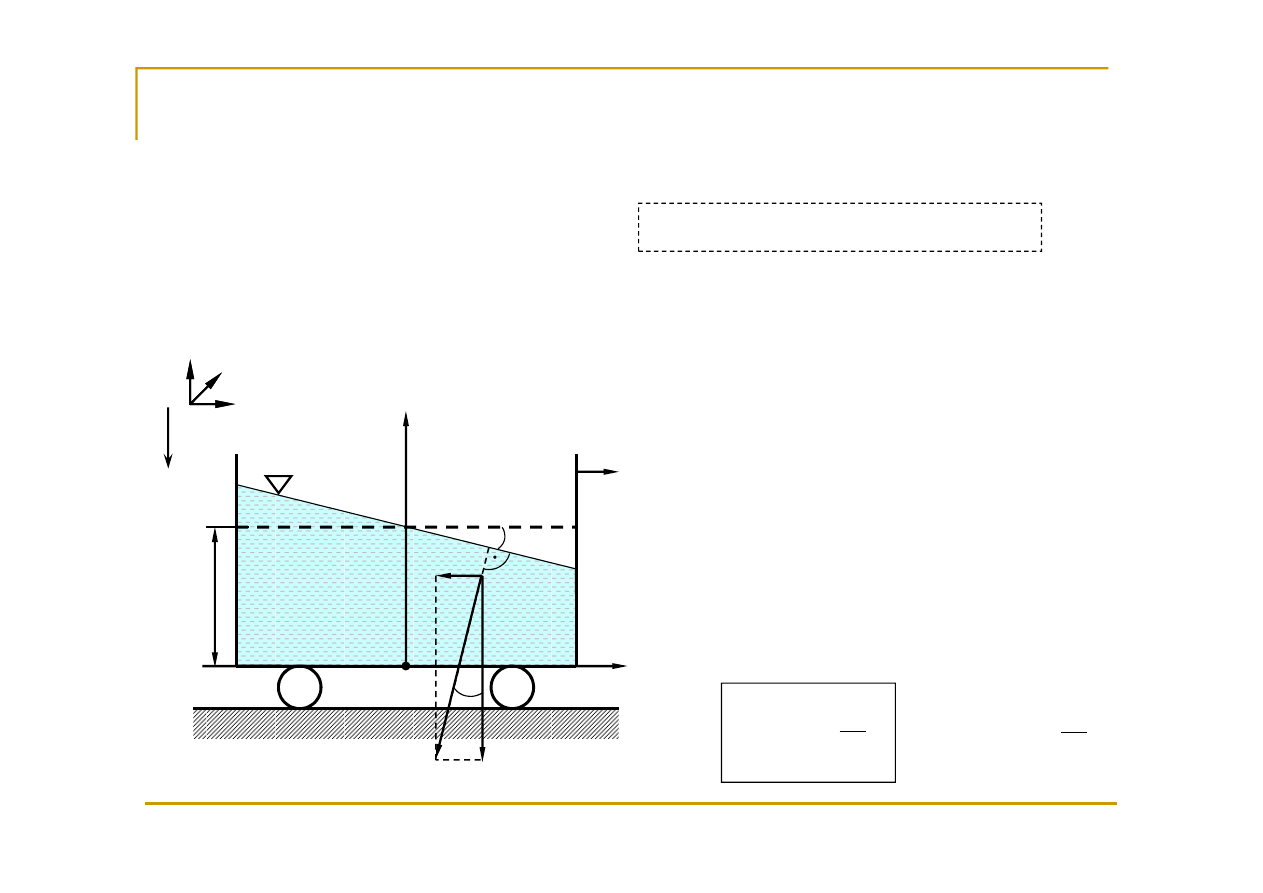
Postępowy ruch naczynia
X
Y
Z
X
Y
Z
g
r
p
z
a
r
Wyznaczenie równania
powierzchni swobodnej
)
d
d
d
(
d
z
Z
y
Y
x
X
p
+
+
=
ρ
0
d
d
=
+
z
g
x
a
0
d
=
p
0
d
d
d
=
+
+
z
Z
y
Y
x
X
powierzchnia swobodna ⇒
g
, Z
a, Y
X
−
=
=
−
=
0
a
p
x
a
r
1
z
1
1
0
dla
gz
C
z
, z
x
=
⇒
=
=
0
d
d
=
+
z
g
x
a
C
gz
ax
=
+
x
g
a
z
z
−
=
1
g
a
=
α
tg
a
r
−
g
r
α
α
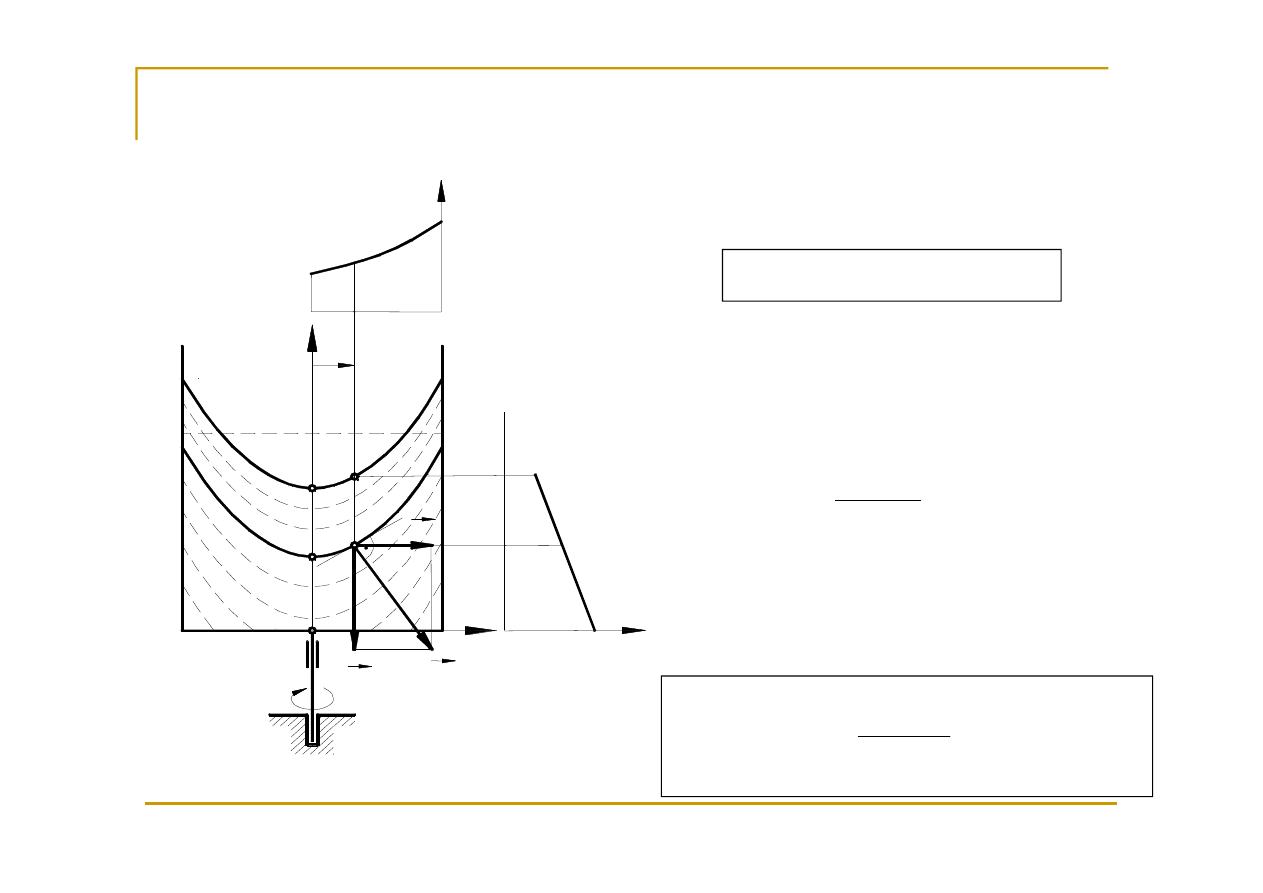
Ruch obrotowy naczynia – wirówki
(
)
dz
g
dr
r
dp
−
=
2
ω
ρ
)
(
dz
Z
dr
X
dp
+
=
ρ
-g
Z
,
2
=
=
ω
r
X
Wyznaczenie ci
ś
nienia
z
p
p
a
r
z
1
C
z
g
r
p
+
−
=
2
2
2
ω
ρ
(
)
−
+
+
=
z
z
g
r
p
p
a
2
2
a
2
ω
ρ
a
a
a
a
ρgz
p
C
p
, p
z
, z
r
dla
+
=
⇒
⇒
=
=
= 0
p
0
a
-g
F
m
r
p
a
z
a
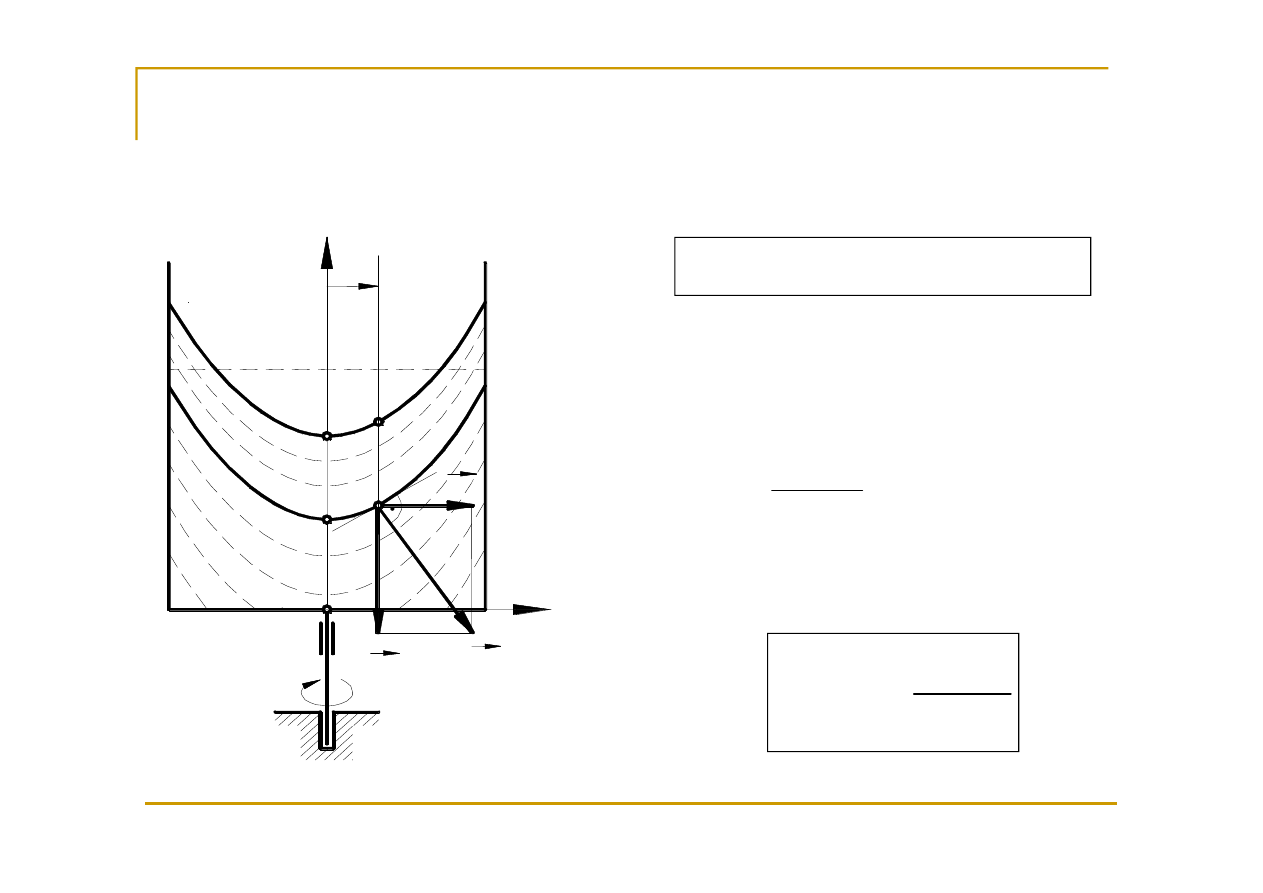
Ruch obrotowy naczynia – wirówki
(
)
0
2
=
−
=
dz
g
dr
r
dp
ω
ρ
0
2
=
− dz
g
dr
r
ω
r
2
2
ω
Wyznaczenie równania powierzchni swobodnej
z
p
a
r
z
a
z
1
a
a
ρgz
C
z
, z
dla r
−
=
⇒
=
= 0
C
z
g
r
=
−
2
2
2
ω
g
r
z
z
2
2
2
a
ω
+
=
0
a
-g
F
m
r
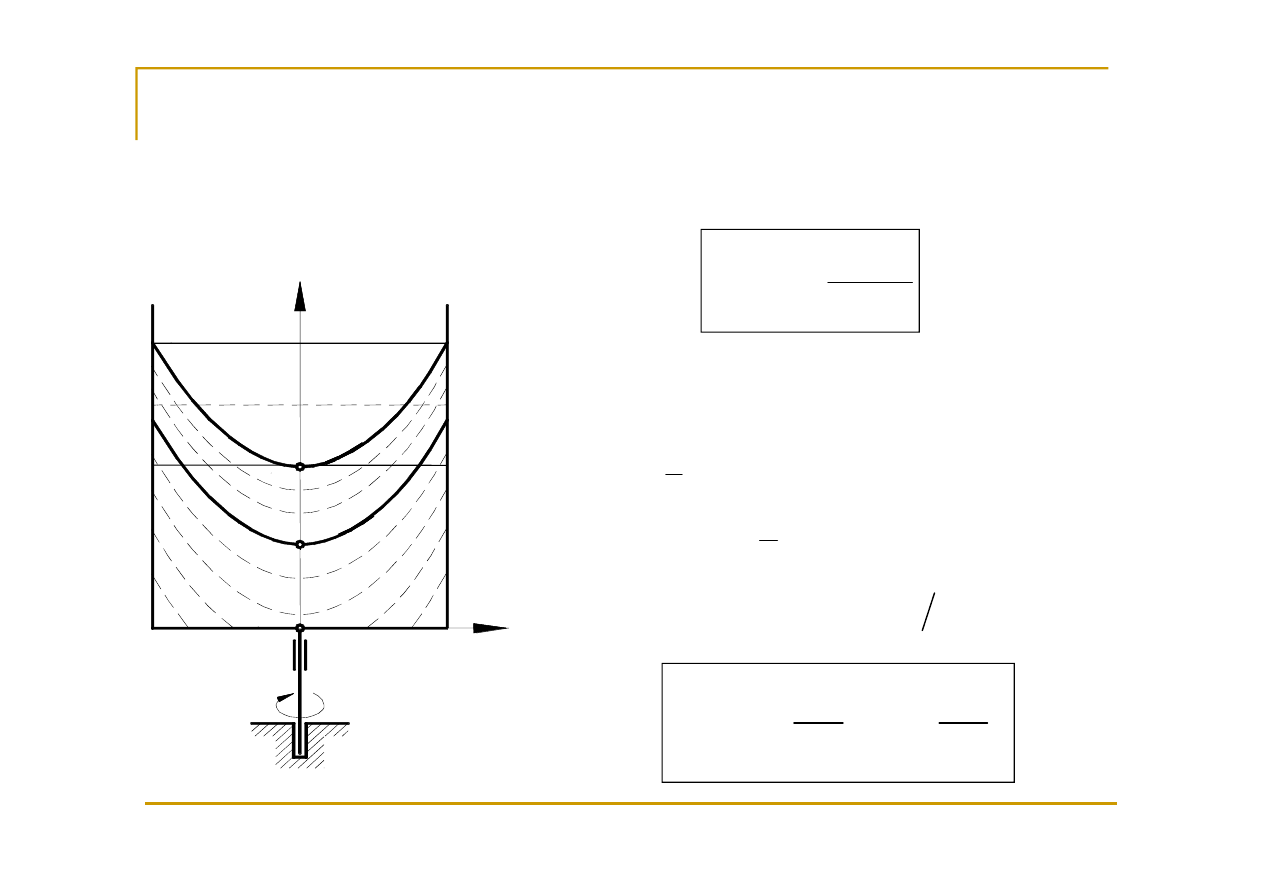
Ruch obrotowy naczynia – wirówki
(
)
(
)
1
g
r
z
z
2
2
2
a
ω
+
=
Objętość pod paraboloidą obrotową jest o połowę mniejsza od
objętości walca cylindrycznego, w który ta paraboloida jest wpisana
Wyznaczenie równania powierzchni swobodnej
z
p
a
z
a
z
1
z
R
(
)
(
)
a
1
2
a
R
2
2
1
z
z
R
z
z
R
−
=
−
π
π
(
)
1
a
R
2
1
z
z
z
=
+
g
R
z
z
4
2
2
1
a
ω
−
=
−
+
=
2
2
2
2
2
1
R
r
g
z
z
ω
0
r
z
a
R
Wyszukiwarka
Podobne podstrony:
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 6
Mechanika płynów dzienne energetyka 30h Wyklad 9
Mechanika płynów dzienne energetyka 30h Wyklad 4
Mechanika płynów dzienne energetyka 30h Wyklad 5
Mechanika płynów dzienne energetyka 30h Wyklad 7
Mechanika płynów dzienne energetyka 30h Wyklad 3
Mechanika płynów dzienne energetyka 30h Wyklad 8
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 3
Mechanika płynów dzienne energetyka 30h Wyklad 9
więcej podobnych podstron