
Mechanika Płynów
Dr Tomasz Wajman
Zespół Maszyn Wodnych i Mechaniki Płynów
Instytut Maszyn Przepływowych PŁ
Pokój 110, tel. 42 631 23 60, (24 54)
E-mail: tomasz.wajman@p.lodz.pl
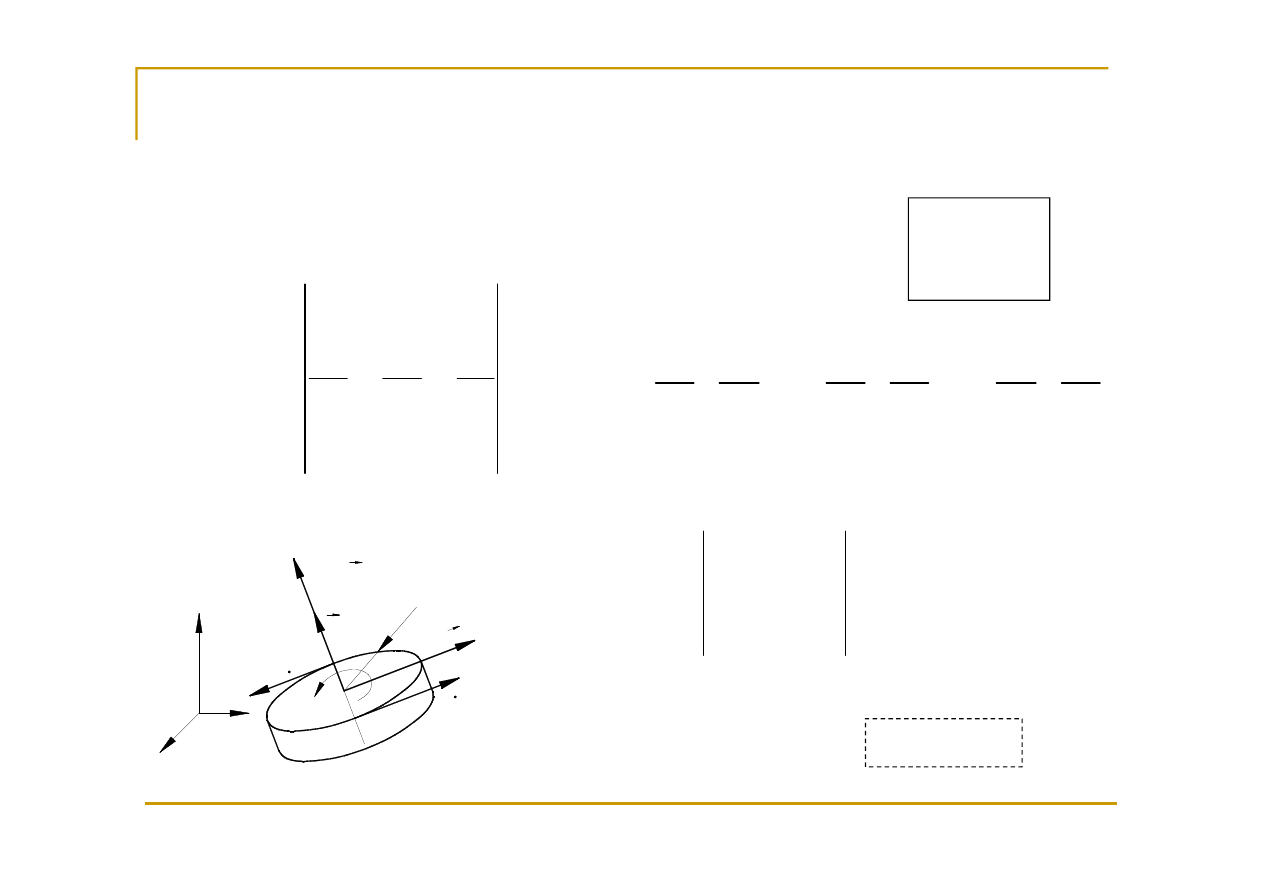
Wirowe i bezwirowe pola prędkości
Pole wirowe jest to takie pole, dla którego niezerowa
jest operacja rotacji wektora pola prędkości.
0
0
rot
≠
×
∇
≠
v
v
r
r
r
v
v
v
z
y
x
k
j
i
v
∂
∂
∂
∂
∂
∂
=
×
∇
r
r
r
r
r
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
=
×
∇
y
v
x
v
k
x
v
z
v
j
z
v
y
v
i
v
x
y
z
x
y
z
r
r
r
r
r
z
y
x
v
v
v
Wirowe pole prędkości ≠ wiry
z
x
y
rot
n
v
n
v
dr
ω
dr
ω
dr
ω
dz
dy
dx
k
j
i
r
d
z
y
x
v
ω
ω
ω
ω
r
r
r
r
r
r
=
×
=
dy
dz
z
y
x
v
ω
ω
−
=
dz
dx
x
z
y
v
ω
ω
−
=
dx
dy
y
x
z
v
ω
ω
−
=
ω
r
r
2
v
rot
=
dr
n
⊥
r
x
x
2
rot
ω
=
v
z
z
2
rot
ω
=
v
y
y
2
rot
ω
=
v
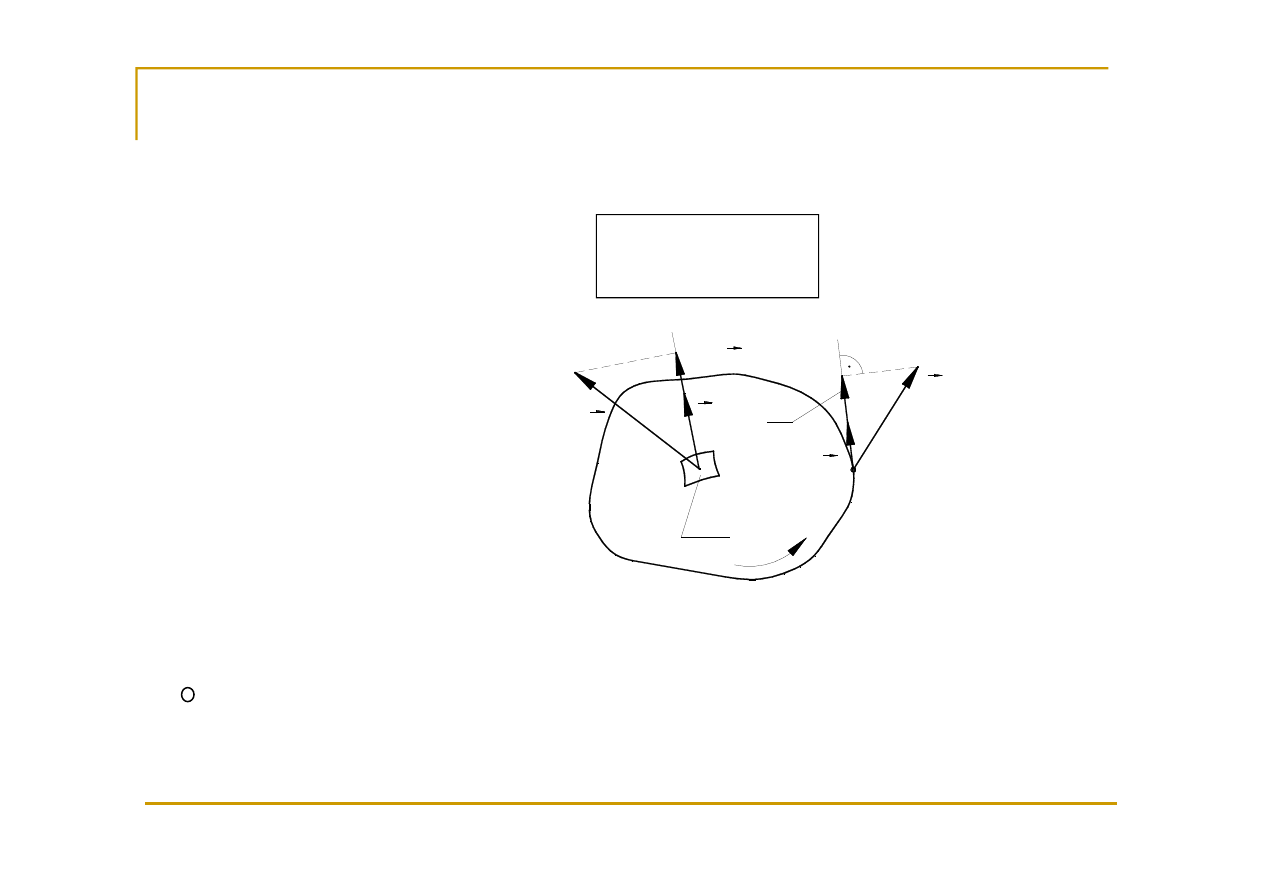
Cyrkulacja prędkości
∫
∫
≡
⋅
=
Γ
B
A
s
B
A
v
v
ds
s
d
r
r
n
v
rot v
v
s
rot
n
v
∫
+
=
Γ
B
y
x
)
dy
v
dx
(v
Dla przypadku płaskiego
Cyrkulację obliczamy po krzywej – otwartej lub zamkniętej.
Dla krzywej otwartej AB mamy:
Gdzie v
s
jest składową styczną.
ds
dA
∫
+
=
Γ
A
y
x
)
dy
v
dx
(v
∫∫
∫
⋅
=
⋅
A
S
v
rot
v
dA
n
s
d
r
r
r
r
Twierdzenie Stokesa
Cyrkulacja prędkości po krzywej zamkniętej
S jest równa strumieniowi rotacji (wirowości)
przechodzącemu przez powierzchnię A
ograniczoną krzywą S.
Ruch bezcryrkulacyjny => ruch bezwirowy

Wirowe i bezwirowe pola prędkości
0
rot
=
v
r
Pole bezwirowe – potencjalne - pole, dla którego rotacja
jest równa zero w całej przestrzeni z wyjątkiem izolowanych
punktów lub linii.
y
v
v
linie
prądu
0
ω
r
r
2
v
rot
=
0
=
ω
r
Elementy nie mają prędkości kątowej.
x
v
v
0
Bezwirowość wiąże się z pominięciem lepkości płynu
– lepkość odpowiada za wirowość płynu/
Elementy nie mają prędkości kątowej.
Poruszają się po torze bez obrotów wokół własnej osi.
Rotacja pola równa zero => pole można przedstawić jako gradient potencjału.
Pole bezwirowe = pole potencjalne
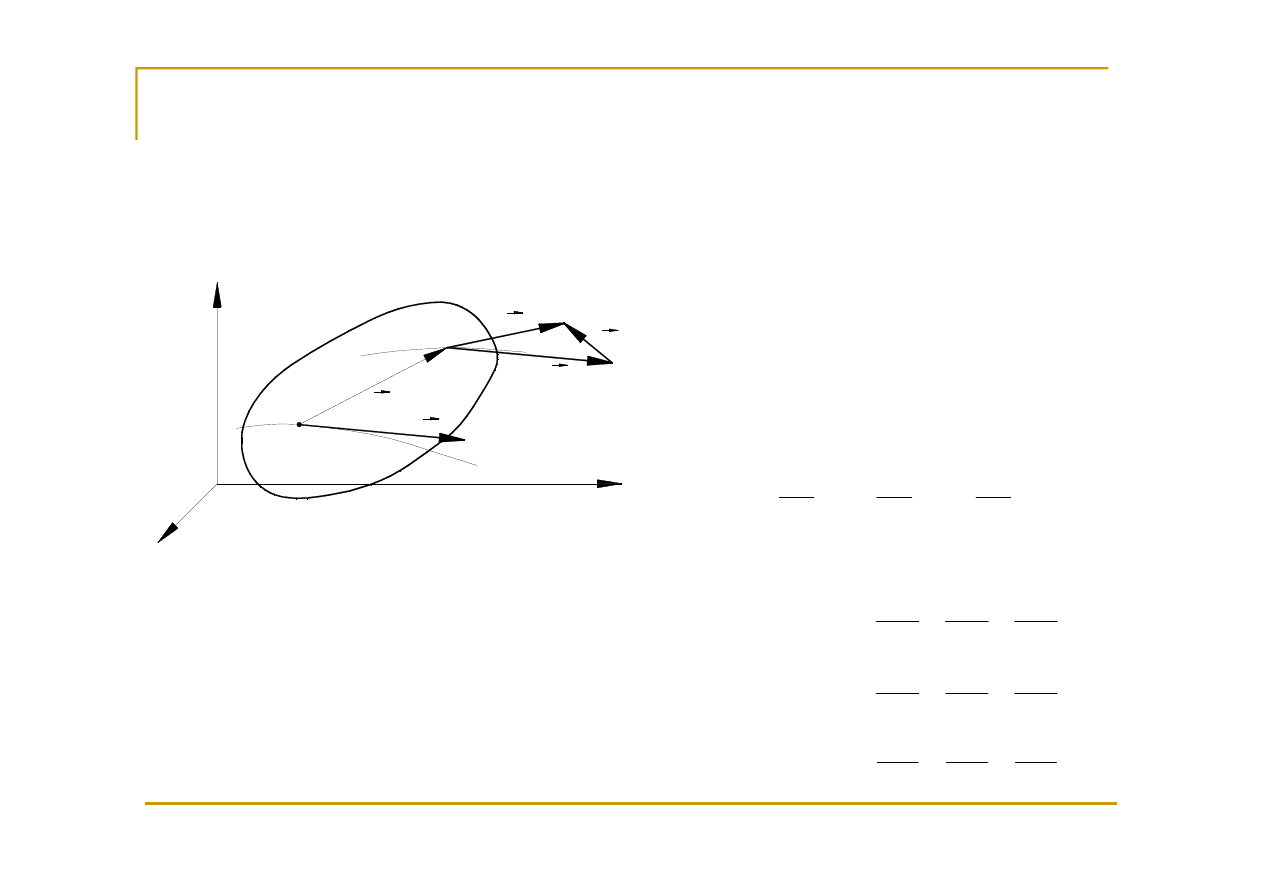
Ruch lokalny płynu
z
∆
r
v
WP
v
P
v
B
P
v
(
)
t
z
y
x
v
v
i
,
,
,
=
r
z
k
y
j
x
i
r
∆
+
∆
+
∆
=
∆
r
r
r
r
)
,
,
,
(
t
z
z
y
y
x
x
P
∆
+
∆
+
∆
+
)
∆
∆
∆
(
t
z,
z
y,
y
x,
x
v
v
Pi
P
+
+
+
=
r
Bryła sztywna – ruch postępowy oraz obrotowy.
Płyn – ruch postępowy, obrotowy oraz deformacja.
prędkość bieguna
x
y
0
B – biegun
)
∆
∆
∆
(
t
z,
z
y,
y
x,
x
v
v
Pi
P
+
+
+
=
z
z
v
y
y
v
x
x
v
v
v
i
i
i
i
Pi
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
+
=
Prędkość względną punktu P względem bieguna B
r
z
y
x
z
y
x
z
y
x
r
v
WP
r
r
r
∆
⋅
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∆
⋅
=
z
z
z
y
y
y
x
x
x
v
v
v
v
v
v
v
v
v
T
WP
P
v
v
v
r
r
r
+
=
T
– tensor prędkości względnej
Tensor prędkości względnej
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
z
y
x
z
y
x
z
y
x
z
z
z
y
y
y
x
x
x
v
v
v
v
v
v
v
v
v
T
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
y
z
y
y
x
x
z
y
x
x
z
z
y
z
x
z
y
y
x
y
z
x
x
y
x
v
v
v
1
v
v
1
v
v
2
1
v
v
v
2
1
v
v
2
1
v
v
2
1
v
S
Tensor prędkości deformacji
(symetryczny)
∂
∂
∂
z
y
x
∂
∂
+
∂
∂
+
∂
z
y
z
x
z
2
2
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
∂
∂
−
∂
∂
=
0
y
v
z
v
2
1
x
v
z
v
2
1
y
v
z
v
2
1
0
x
v
y
v
2
1
x
v
z
v
2
1
x
v
y
v
2
1
0
z
y
z
x
z
y
y
x
z
x
y
x
Ω
Tensor prędkości obrotu
(antysymetryczny)
Ω
S
+
=
T
.
.
. p
e
wir
v
r
r
r
r
r
r
=
∆
×
=
∆
⋅
ω
Ω
Prędkość wirowania elementu płynu wokół własnej osi
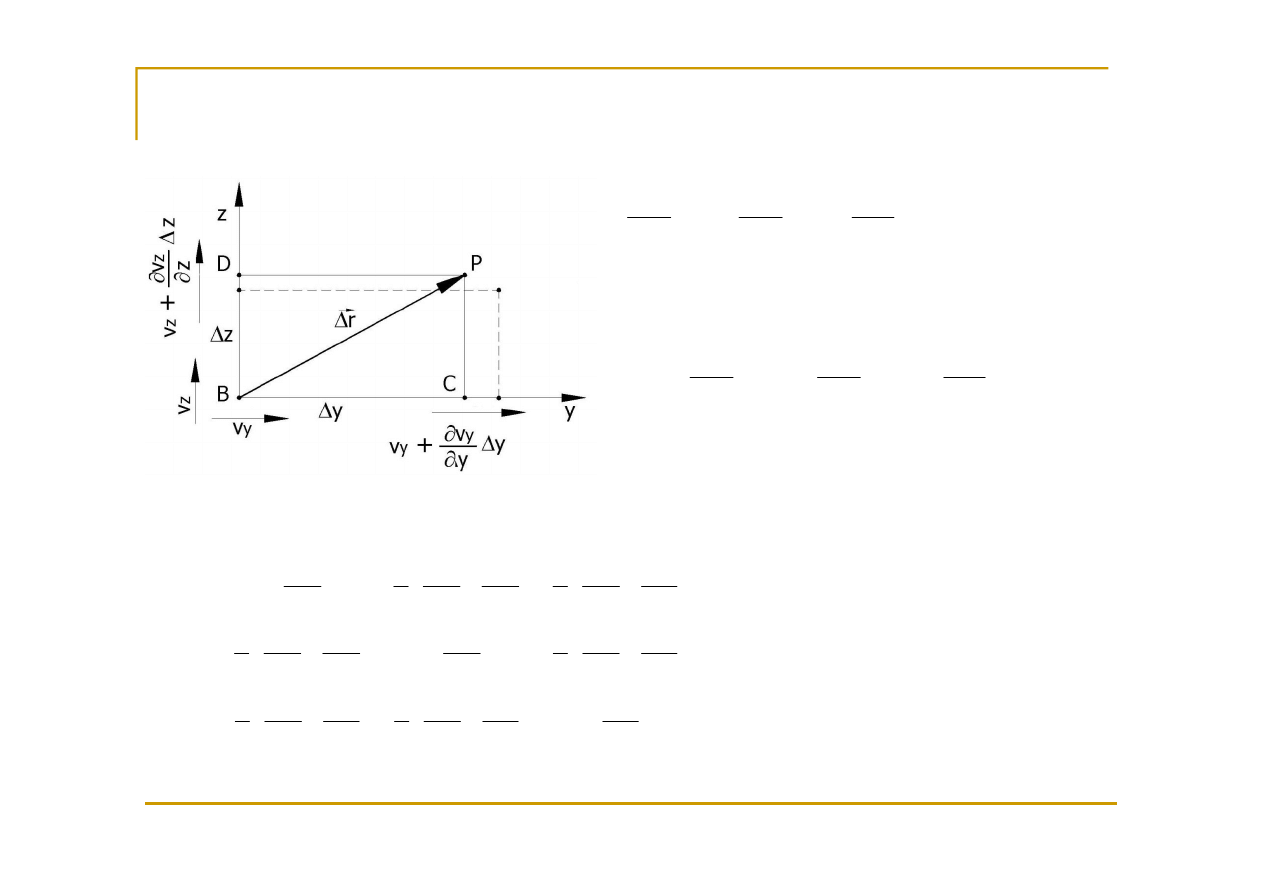
Ruch lokalny płynu
z
z
y
y
x
x
∆
∂
∂
∆
∂
∂
∆
∂
∂
z
y
x
v
,
v
,
v
Prędkości deformacji liniowej elementu płynu
w kierunku osi x, y i z.
z
y
x
∂
∂
=
∂
∂
=
∂
∂
=
z
z
y
y
x
x
v
,
v
,
v
ε
ε
ε
Prędkości względnej deformacji liniowej
elementu płynu w kierunku osi x, y i z.
r
z
y
z
x
z
y
z
y
y
x
x
z
y
x
x
r
r
r
∆
⋅
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∆
⋅
z
z
y
z
x
z
y
y
x
y
z
x
x
y
x
v
v
v
2
1
v
v
2
1
v
v
2
1
v
v
v
2
1
v
v
2
1
v
v
2
1
v
S
elementu płynu w kierunku osi x, y i z.
v
r
r
⋅
∇
=
+
+
z
y
x
ε
ε
ε
Względna prędkość deformacji
objętościowej elementu płynu.
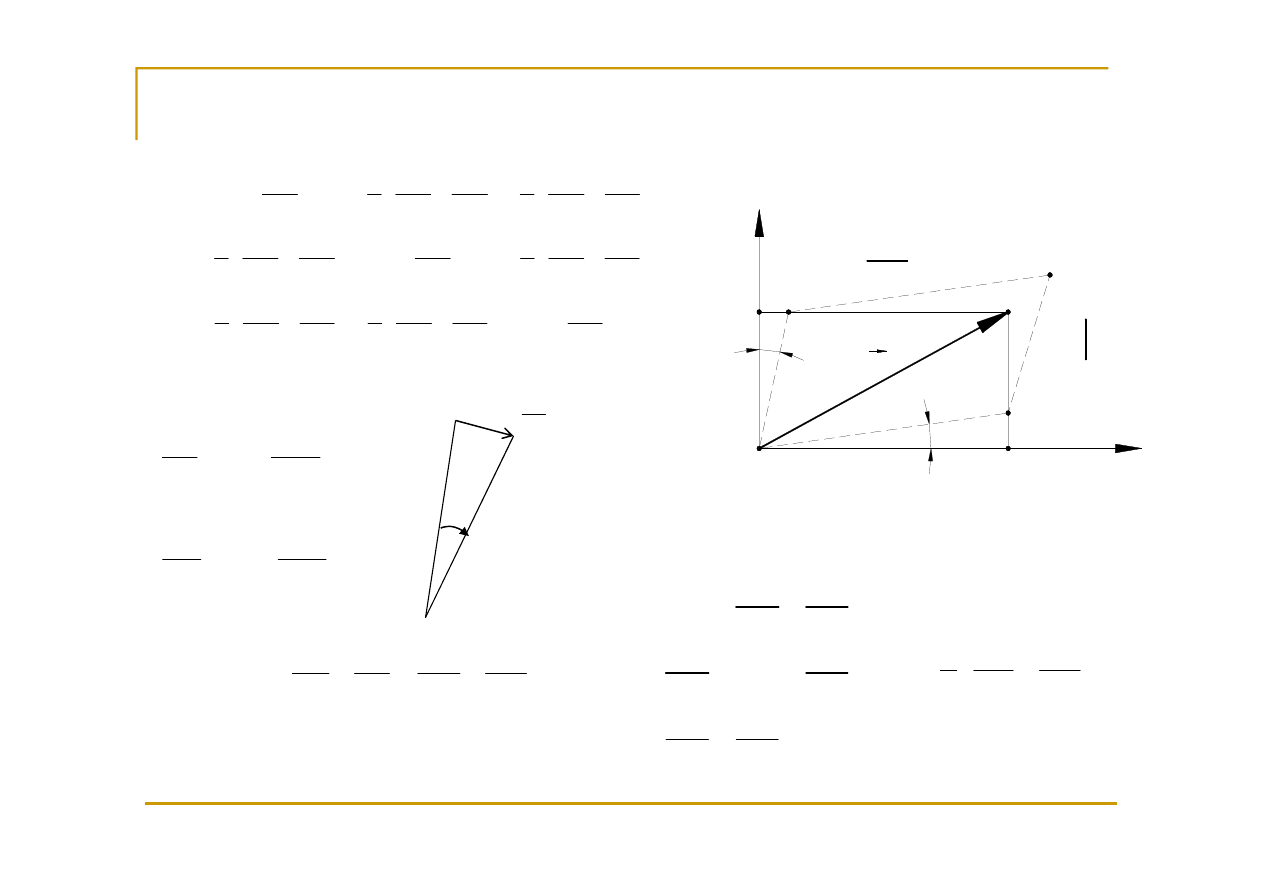
Ruch lokalny płynu
z
∆
r
B
P
v
y
+
∂
v
y
∂
z
∆
z
D
v
z
+
∂
v
z
∂
y
∆
y
∆
∆
z
d
β
z
v
z
d
y
∆
∂
=
∆
β
r
z
y
z
x
z
y
z
y
y
x
x
z
y
x
x
r
r
r
∆
⋅
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∆
⋅
z
z
y
z
x
z
y
y
x
y
z
x
x
y
x
v
v
v
2
1
v
v
2
1
v
v
2
1
v
v
v
2
1
v
v
2
1
v
v
2
1
v
S
z
d
d
∆
=
∆
t
v
y
β
y
B
C
∆
y
d
α
y
y
v
y
dt
d
z
∆
∂
∂
=
∆
α
z
z
v
z
dt
d
y
∆
∂
∂
=
∆
β
y
z
dt
d
dt
d
∂
∂
+
∂
∂
=
+
=
Θ
=
Θ
z
y
zy
yz
v
v
β
α
Zmiana kąta DBC, deformacji postaciowa
β
Θ
Θ
Θ
Θ
Θ
Θ
=
z
zy
zx
yz
y
yx
xz
xy
x
2
2
2
2
2
2
ε
ε
ε
S
∂
∂
+
∂
∂
=
i
j
j
i
ij
v
v
x
x
S
2
1
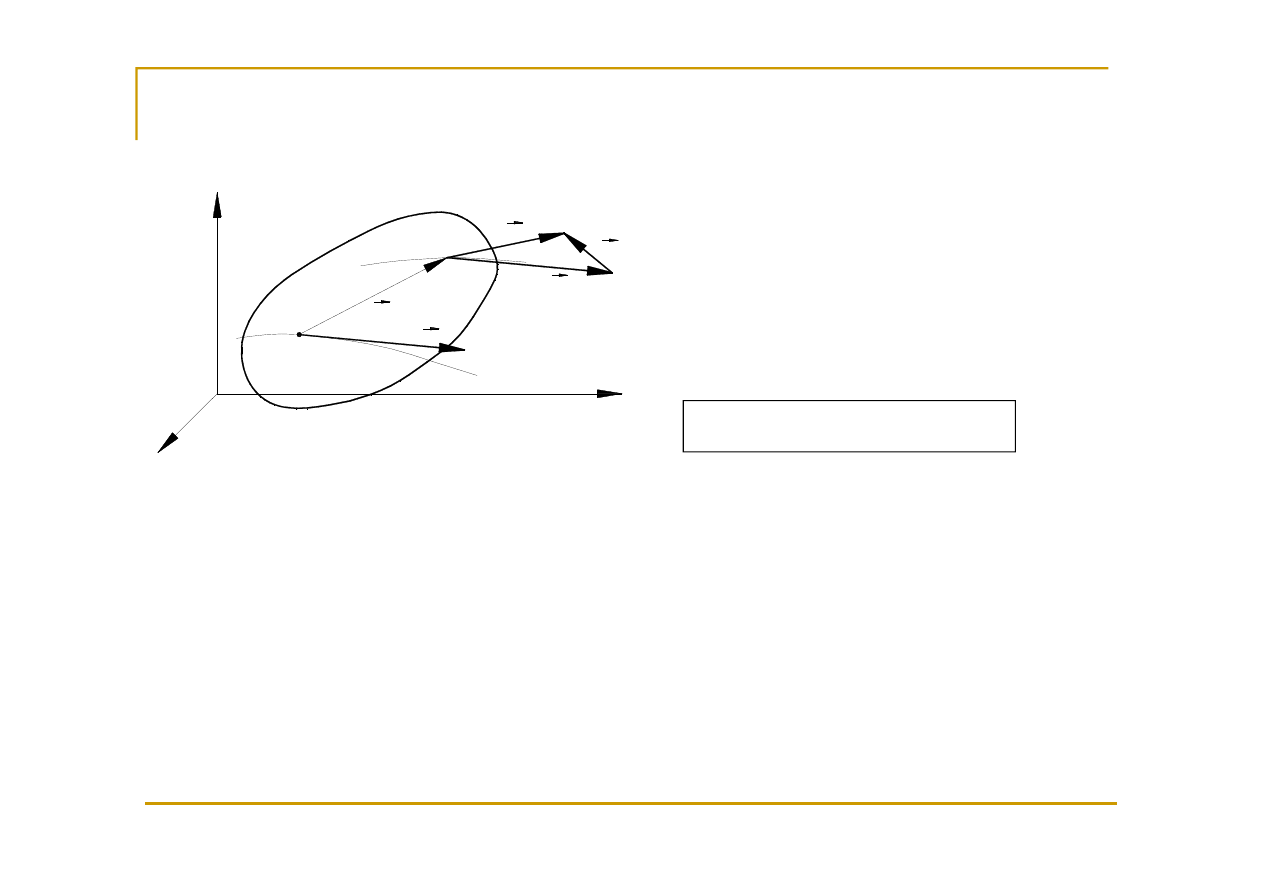
Twierdzenie Helmholtza
r
r
ω
v
v
B
P
r
r
r
r
r
S∆
∆
+
×
+
=
z
x
y
∆
r
v
WP
v
P
v
B
P
v
0
WP
P
v
v
v
r
r
r
+
=
(
)
r
r
v
WP
r
r
r
∆
⋅
+
=
∆
⋅
=
Ω
S
T
B
P
Prędkość punktu P znajdującego się w elemencie płynu
możemy przedstawić jako sumę wektorową
prędkości postępowej bieguna B
plus prędkości względnej wynikającej z obrotu wokół B
i deformacji.
x

Dynamika
płynów
płynów
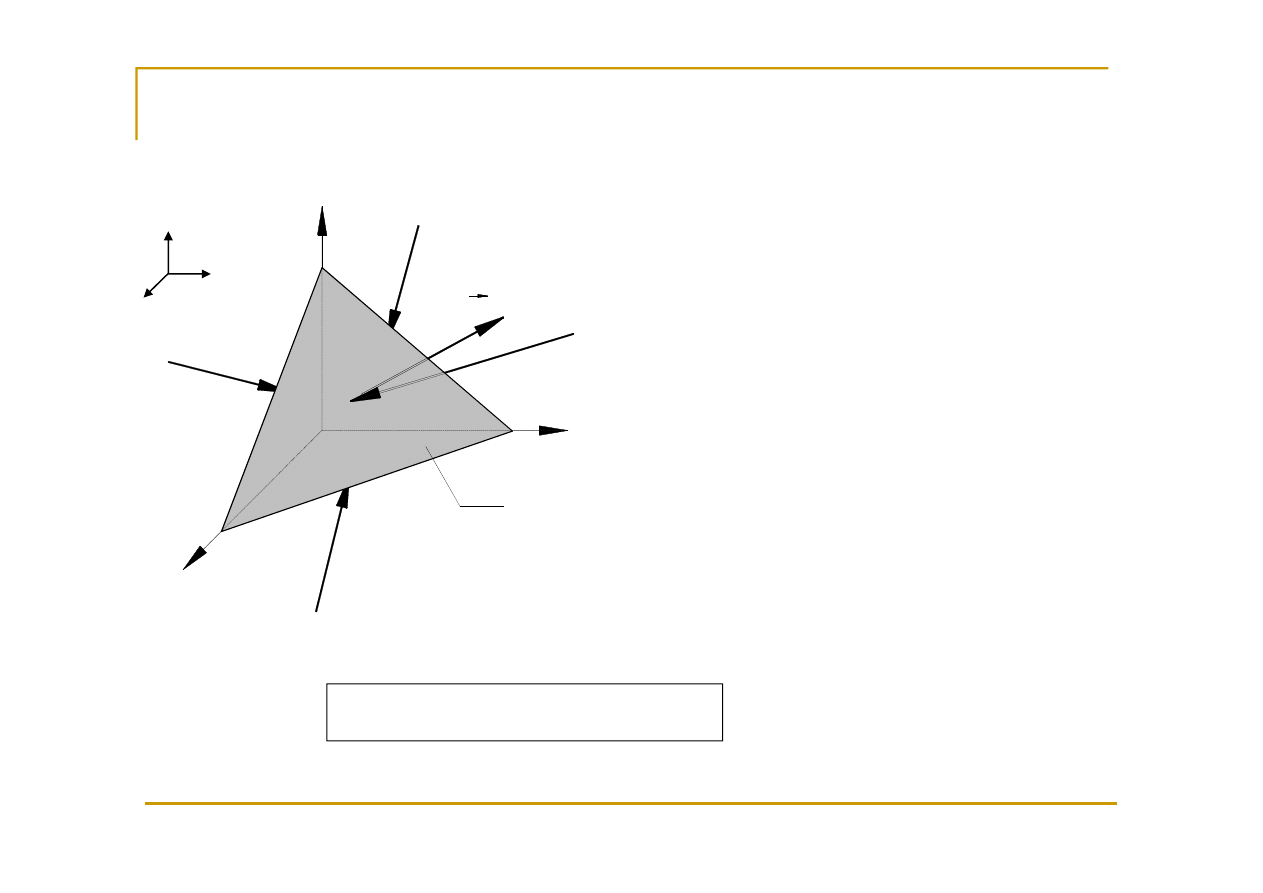
Siły powierzchniowe, tensor naprężeń
0
d
d
d
d
=
−
−
−
z
z
y
y
x
x
n
A
p
A
p
A
p
A
p
r
r
r
r
y
p
r
z
y
n
n
p
r
x
p
r
x
dA
y
dA
i
r
j
r
k
r
k
j
i
r
r
r
−
−
−
,
,
n
p
r
z
y
x
p
,
p
,
p
r
r
r
lokalna równowaga sił powierzchniowych
Wektor naprężenia
=
=
=
z
z
y
y
x
x
n
A
A
n
A
A
n
A
A
d
d
d
d
d
d
z
y
x
n
k
n
j
n
i
n
r
r
r
r
+
+
=
z
z
y
y
x
x
n
n
p
n
p
n
p
p
r
r
r
r
+
+
=
+
+
=
+
+
=
+
+
=
zz
zy
zx
z
yz
yy
yx
y
xz
xy
xx
x
p
k
τ
j
τ
i
p
τ
k
p
j
τ
i
p
τ
k
τ
j
p
i
p
r
r
r
r
r
r
r
r
r
r
r
r
z
p
r
y
x
A
d
z
dA
lokalna równowaga sił powierzchniowych
Siły powierzchniowe, tensor naprężeń
+
+
=
+
+
=
+
+
=
zz
z
yz
y
xz
x
nz
zy
z
yy
y
xy
x
ny
zx
z
yx
y
xx
x
nx
p
n
τ
n
τ
n
p
τ
n
p
n
τ
n
p
τ
n
τ
n
p
n
p
=
∏
zx
yx
xx
df
τ
p
τ
τ
τ
p
z
z
y
y
x
x
n
n
p
n
p
n
p
p
r
r
r
r
+
+
=
+
+
=
+
+
=
+
+
=
zz
zy
zx
z
yz
yy
yx
y
xz
xy
xx
x
p
k
τ
j
τ
i
p
τ
k
p
j
τ
i
p
τ
k
τ
j
p
i
p
r
r
r
r
r
r
r
r
r
r
r
r
=
∏
zz
yz
xz
zy
yy
xy
p
τ
τ
τ
p
τ
Π
n
p
n
r
r
=
zx
xz
τ
τ
=
xy
yx
τ
τ
=
zy
yz
τ
τ
=
Tensor napr
ęż
e
ń
powierzchniowych
Wektor naprężenia
można pokazać, że jest to
tensor symetryczny:
Przy braku ruchu płynu (statyka) oraz
podczas przepływu płynu nielepkiego
p
p
p
p
zz
yy
xx
=
=
=
Wyszukiwarka
Podobne podstrony:
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 6
Mechanika płynów dzienne energetyka 30h Wyklad 9
Mechanika płynów dzienne energetyka 30h Wyklad 4
Mechanika płynów dzienne energetyka 30h Wyklad 5
Mechanika płynów dzienne energetyka 30h Wyklad 7
Mechanika płynów dzienne energetyka 30h Wyklad 1
Mechanika płynów dzienne energetyka 30h Wyklad 3
Mechanika płynów dzienne energetyka 30h Wyklad 8
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 9
więcej podobnych podstron