
Mechanika płynów
Dr Tomasz Wajman
Dr Tomasz Wajman
Zespół Maszyn Wodnych i Mechaniki Płynów
Instytut Maszyn Przepływowych PŁ
E-mail: tomasz.wajman@p.lodz.pl

Reakcja hydrodynamiczna
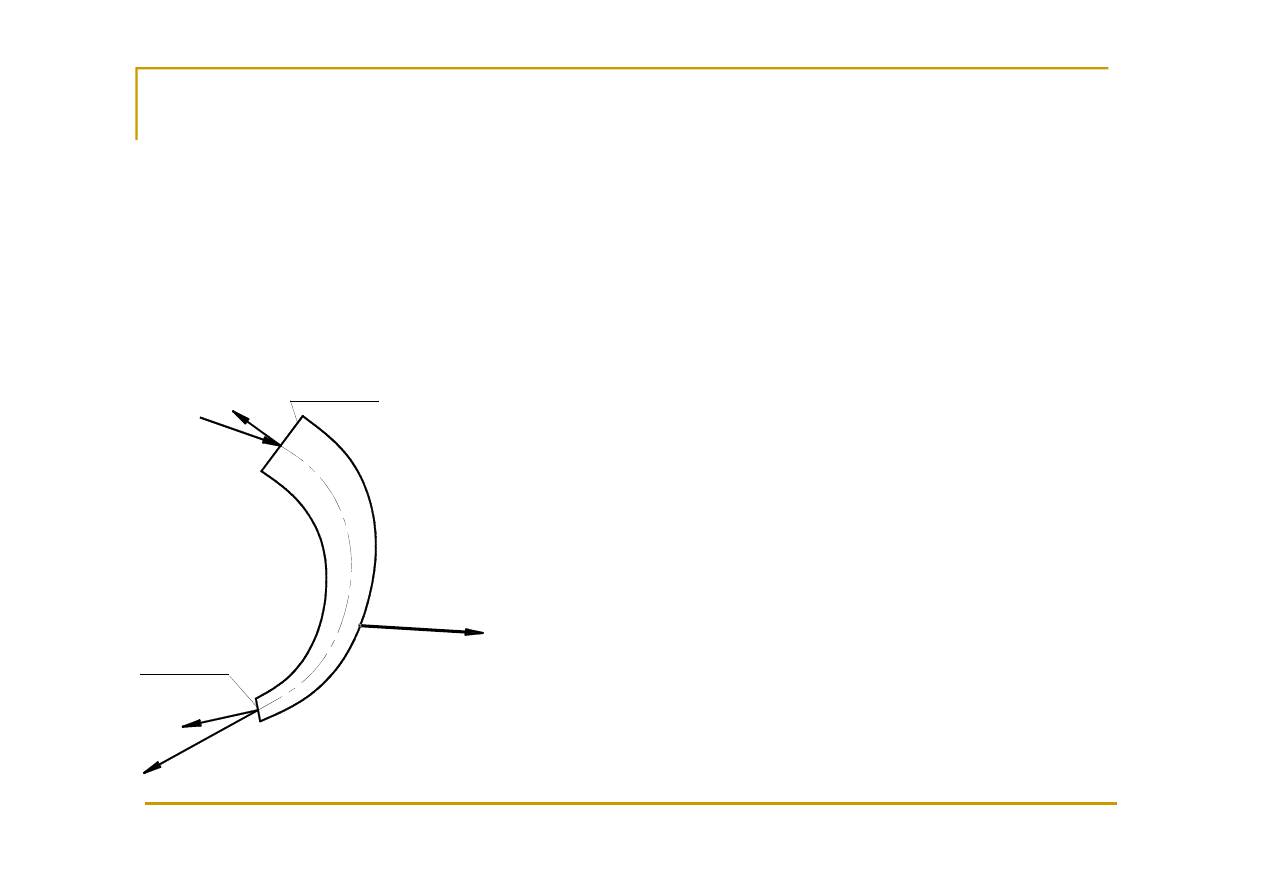
Reakcje na ścianki kanałów
∫∫
∫∫
∫∫
+
+
−
=
+
−
b
A
A
A
A
n
A
n
A
p
n
A
v
v
ρ
A
v
v
ρ
2
1
2
1
d
d
d
2
2
2
2
1
1
1
1
r
r
r
∫∫∫
∫∫
∫∫
+
=
V
m
A
n
n
A
V
ρ
F
A
p
A
v
v
ρ
d
d
d
r
r
r
Równanie pędu
w ruchu ustalonym
1
1
1
,
,
p
A
ρ
1
v
r
1
n
r
∫∫
=
b
A
b
A
p
n
R
d
r
r
Reakcja oddziaływania
płynu na ścianki
2
2
2
,
,
p
A
ρ
2
v
r
2
n
r
R
r
b
A
A
A
A
A
A
A
p
n
A
p
n
A
p
n
A
p
n
b
d
d
d
d
2
2
2
1
1
1
2
1
3
2
1
∫∫
∫∫
∫∫
∫∫
+
+
=
+
+
r
r
r
r
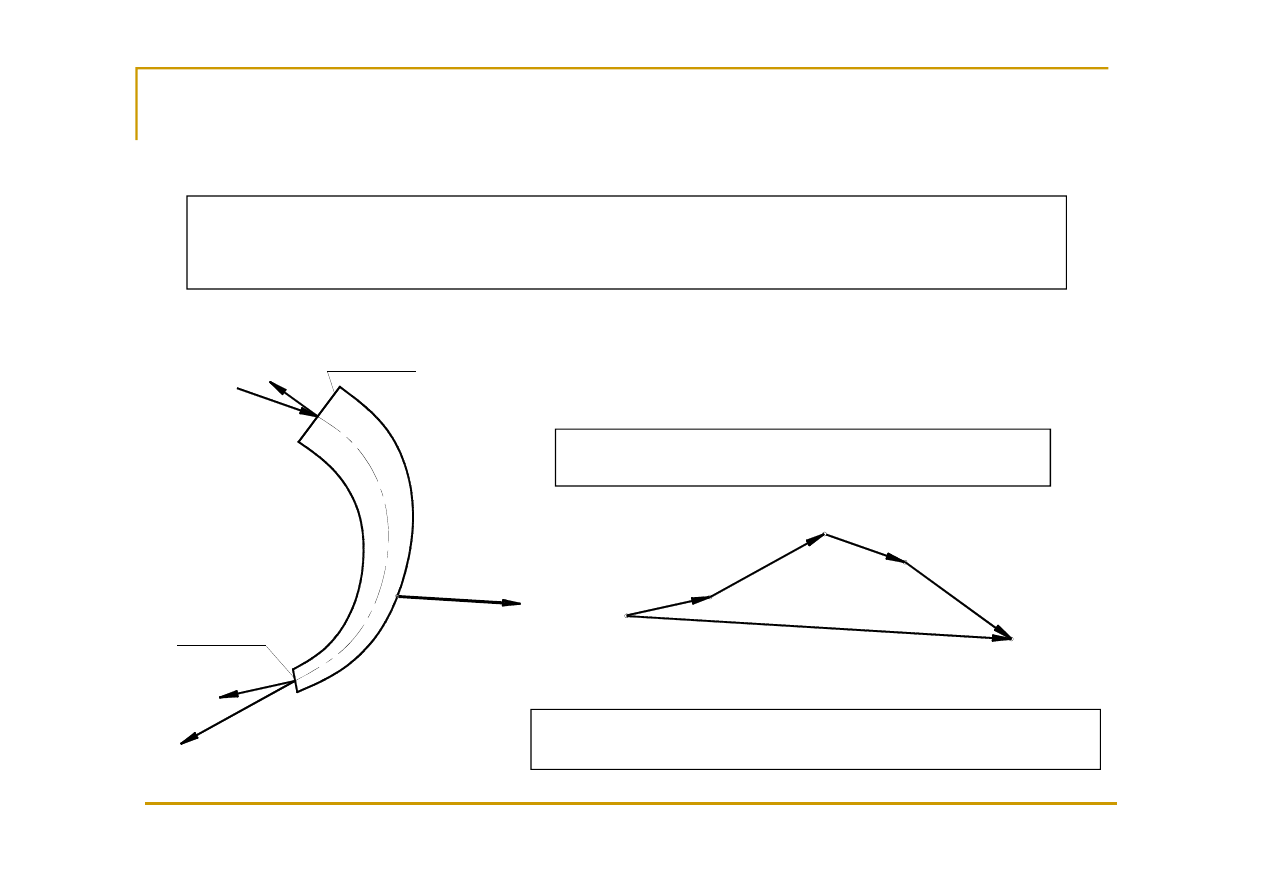
Reakcje na ścianki kanałów
(
)
A
p
n
A
p
n
v
v
m
R
r
r
r
r
&
r
−
−
−
=
Dla jednorodnych pól parametrów
w przekrojach kontrolnych:
2
2
2
1
1
1
2
2
2
2
1
1
1
1
d
d
d
d
2
1
2
1
A
p
n
A
p
n
A
v
v
ρ
A
v
v
ρ
R
A
A
n
A
n
A
∫∫
∫∫
∫∫
∫∫
−
−
−
=
r
r
r
r
r
1
1
1
,
,
p
A
ρ
1
v
r
1
n
r
(
)
2
2
2
1
1
1
2
1
A
p
n
A
p
n
v
v
m
R
r
r
r
r
&
r
−
−
−
=
(
)
2
2
2
1
1
1
2
1
A
p
n
A
p
n
v
v
m
R
netto
∆
−
∆
−
−
=
r
r
r
r
&
r
2
2
2
,
,
p
A
ρ
2
v
r
2
n
r
R
r
R
r
2
2
2
A
p
n
r
−
1
1
1
A
p
n
r
−
1
v
m
r
&
2
v
m
r
&
−
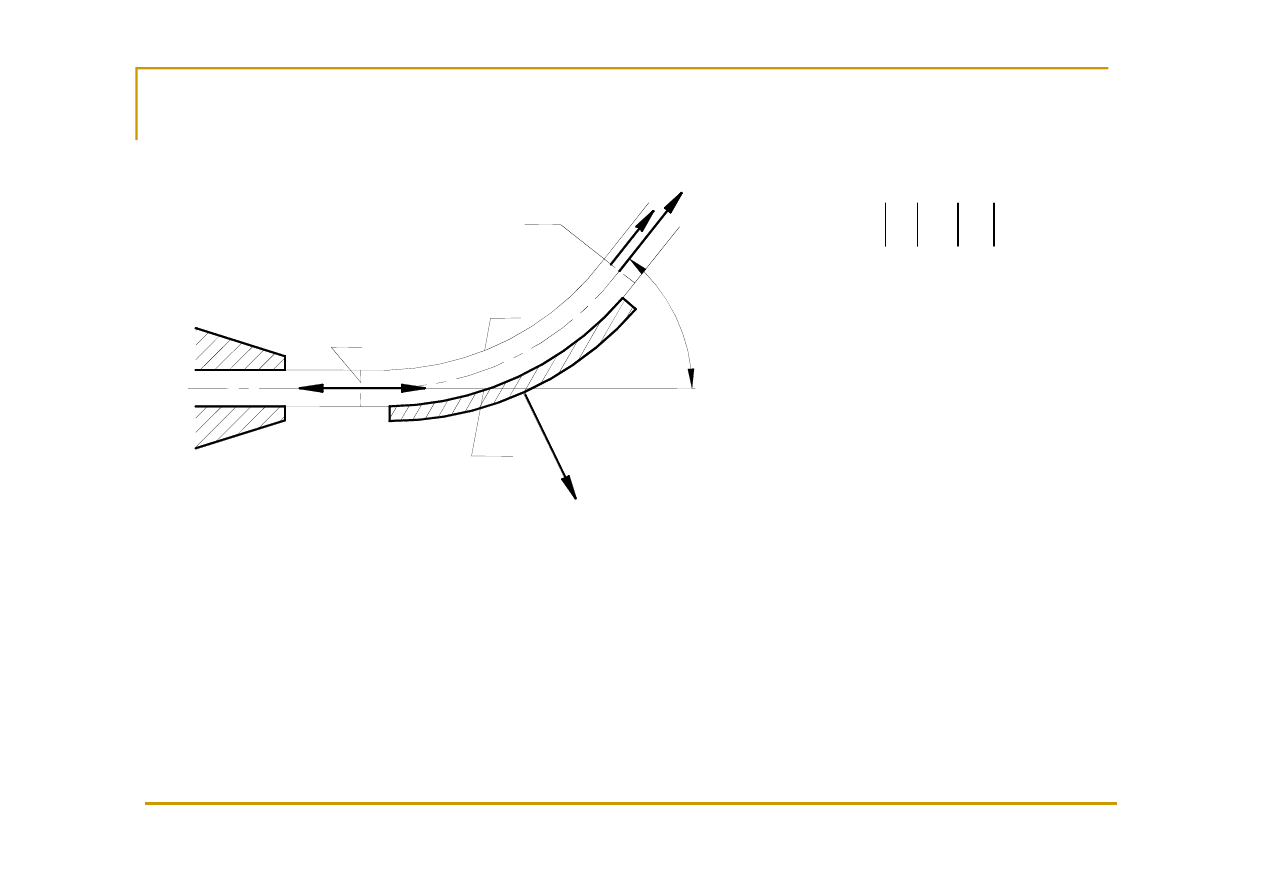
Reakcje na opływanie ciała
v
v
v
=
=
2
1
r
r
0
d
2
1
=
∫∫
+
+
+
b
S
A
A
A
A
a
A
n
p
r
a
p
1
v
r
1
n
r
2
A
2
v
r
2
n
r
1
A
a
p
S
A
b
A
α
n
R
r
b
A
∫∫
∫∫
∫∫
+
+
+
−
=
+
−
b
S
A
A
A
A
A
n
A
n
A
p
n
A
v
v
ρ
A
v
v
ρ
2
1
2
1
d
d
d
2
2
2
2
1
1
1
1
r
r
r
(
)
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∆
=
∆
+
+
=
+
=
+
+
+
+
+
+
+
b
b
S
b
S
b
S
A
A
a
A
A
A
a
A
A
A
A
a
A
A
A
A
A
p
n
A
p
p
n
A
p
n
A
p
n
A
p
n
A
p
n
d
d
d
d
d
d
2
1
2
1
2
1
r
r
r
r
r
r
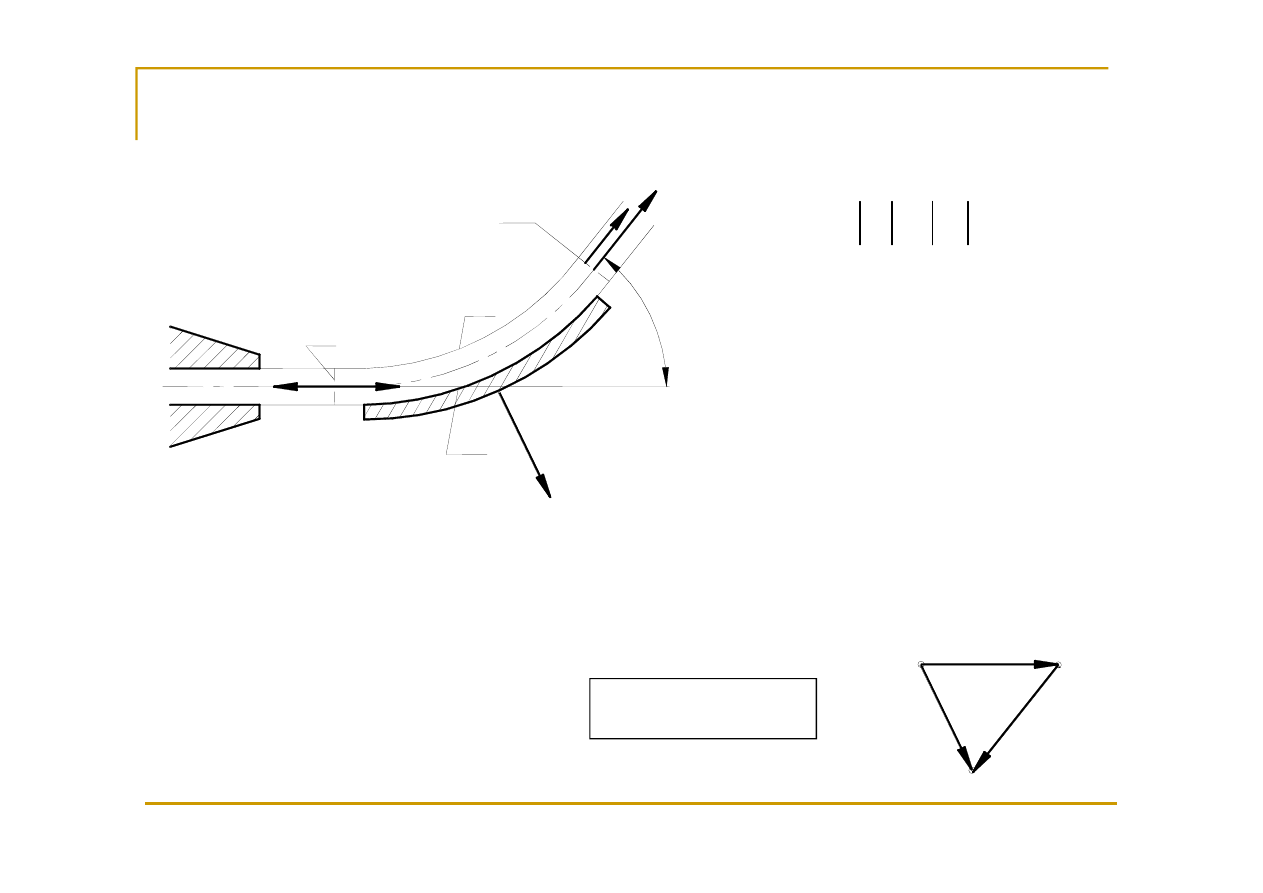
Reakcje na opływanie ciała
v
v
v
=
=
2
1
r
r
0
d
2
1
=
∫∫
+
+
+
b
S
A
A
A
A
a
A
n
p
r
a
p
1
v
r
1
n
r
2
A
2
v
r
2
n
r
1
A
a
p
S
A
b
A
α
n
R
r
(
)
n
b
a
A
b
A
A
A
R
A
p
p
n
A
p
n
A
v
v
ρ
A
v
v
ρ
b
b
r
r
r
r
r
−
=
−
−
=
∆
−
=
+
−
∫∫
∫∫
∫∫
∫∫
d
d
d
d
2
2
2
1
1
1
2
1
(
)
b
a
A
n
A
p
p
n
R
b
d
−
=
∫∫
r
r
(
)
2
1
v
v
m
R
n
r
r
&
r
−
=
b
A
n
R
r
1
v
m
r
&
2
v
m
r
&
−
Reakcje na opływanie ciała
3
2
m
m
m
&
&
&
+
=
v
v
v
v
=
=
=
3
2
1
r
r
r
2
3
m
m
&
& <
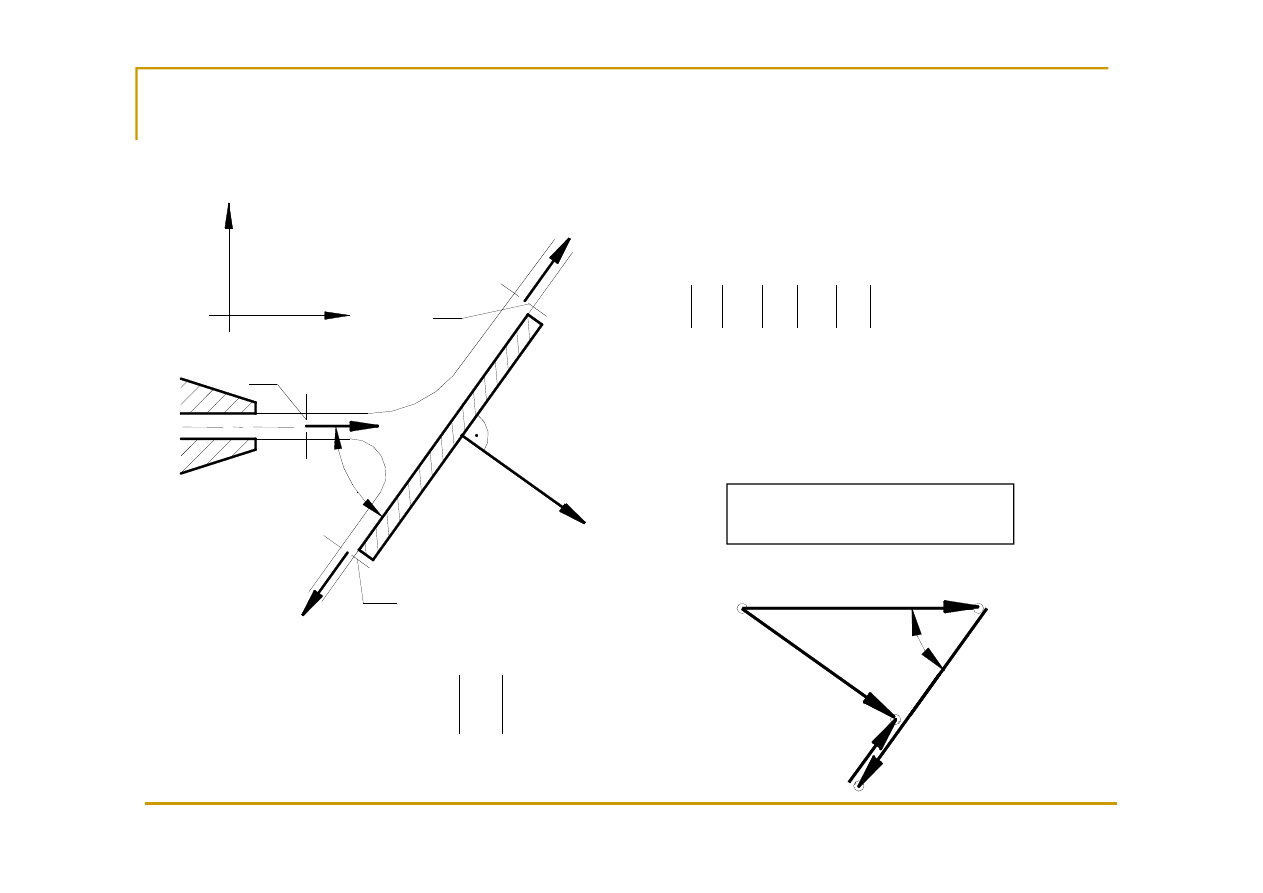
Płyn nielepki – składowe styczne
sił równe zero
1
A
2
A
1
v
r
2
v
r
x
y
α
v
m
R
n
sin
⋅
⋅
= &
r
n
R
r
3
A
3
v
r
α
(
)
3
2
1
v
v
v
m
R
n
r
r
r
&
r
−
−
=
n
R
r
1
v
m
r
&
2
v
m
r
&
−
3
v
m
r
&
−
α
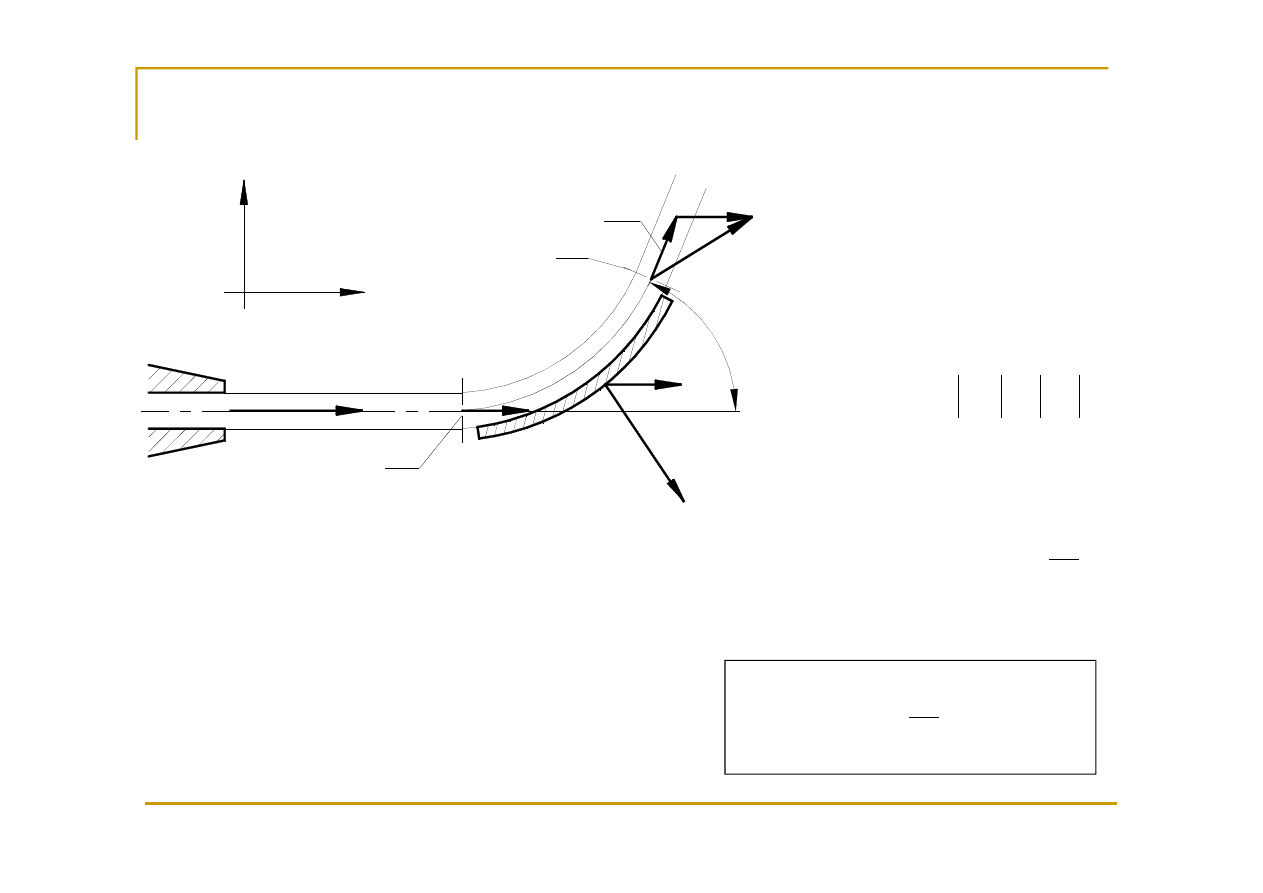
Reakcje na powierzchnie ruchome
u
v
w
r
r
r
−
=
1
1
1
2
w
w
r
r
=
x
y
a
p
1
v
r
2
A
2
v
r
A
α
R
r
u
r
1
w
r
2
w
r
u
r
(
)
−
=
−
=
=
1
1
1
1
1
1
v
u
m
A
ρ
u
v
A
ρ
w
m
w
&
&
(
)
2
1
1
1
w
w
v
u
m
R
nw
r
r
&
r
−
−
=
1
A
a
p
nw
R

Podobieństwo zjawisk
przepływowych
przepływowych

Podobieństwo zjawisk fizycznych
Badania eksperymentalne często prowadzi się na obiektach modelowych,
najczęściej zmniejszonych w odniesieniu do obiektów naturalnych.
Warunki podobieństwa:
- geometryczne (skala podobieństwa geometrycznego)
- kinematyczne (podobieństwo pól prędkości)
- dynamiczne

Główne twierdzenie
o podobieństwie zjawisk
Zjawisko fizyczne jest opisywane przez zestaw pól parametrów fizycznych.
Każde pole fizyczne można przedstawić w postaci bezwymiarowej, dzieląc funkcję
opisującą to pole przez wybraną charakterystyczną wartość tej funkcji.
Dla pola prędkości np. używamy prędkości przepływu niezaburzonego
lub średniej prędkości przepływu przez kanał.
Jeśli dwa porównywalne zjawiska opisane są w formie
bezwymiarowej identycznym układem równań różniczkowych
i warunków brzegowych, to zjawiska te są podobne
.
Dwa pola fizyczne nazywamy podobnymi, jeśli przedstawione w postaci
bezwymiarowej (w opisany powyżej sposób) są identyczne.

Główne twierdzenie
o podobieństwie zjawisk
∂
+
∂
+
∂
+
∂
−
=
∂
+
∂
+
∂
+
∂
2
2
2
1
v
v
v
p
X
v
v
v
v
v
v
v
x
x
x
x
x
x
x
υ
v
p
ρ
F
t
v
m
r
r
r
2
grad
1
d
d
∇
+
−
=
υ
0
div
=
v
r
υρ
=
=
.
const
µ
Równanie Naviera-Stokesa dla płynu nieściśliwego
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
2
2
2
1
z
v
y
v
x
v
x
p
ρ
X
z
v
v
y
v
v
x
v
v
t
v
x
x
x
x
z
x
y
x
x
x
υ
Charakterystyczne wielkości odniesienia:
- liniowy wymiar charakterystyczny, np. średnica kanału,
- czas charakterystyczny, np. okres dla zjawisk periodycznych,
- prędkość odniesienia, np. prędkość średnia w kanale,
- ciśnienie i gęstość odniesienia odpowiadająca prędkości,
- przyspieszenie ziemskie, parametr odniesienia dla sił masowych.
0
l
0
t
0
v
0
0
,
ρ
p
g

Główne twierdzenie
o podobieństwie zjawisk
0
ˆ
t
t
t
=
0
0
0
ˆ
,
ˆ
,
ˆ
l
z
z
l
y
y
l
x
x
=
=
=
0
0
0
ˆ
,
ˆ
,
ˆ
v
v
v
v
v
v
v
v
v
z
z
y
y
x
x
=
=
=
Parametry bezwymiarowe:
geometryczne -
czasu -
pr
ę
dko
ś
ci -
g
X
X
=
ˆ
0
0
ˆ
,
ˆ
ρ
ρ
ρ
=
=
p
p
p
sił masowych -
ci
ś
nienia i g
ę
sto
ś
ci -
t
v
t
v
t
v
x
o
o
x
ˆ
ˆ
∂
∂
=
∂
∂
x
o
x
v
v
v
ˆ
=
t
t
t
o
ˆ
=
2
2
2
2
2
ˆ
ˆ
x
v
l
v
υ
x
v
υ
x
o
o
x
∂
∂
=
∂
∂
x
l
x
o
ˆ
=

Kryteria podobieństwa przepływów
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
2
2
2
2
2
2
2
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
1
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
z
v
y
v
x
v
l
v
x
p
ρ
ρ
l
p
X
g
z
v
v
y
v
v
x
v
v
l
v
t
v
t
v
x
x
x
o
o
o
o
o
x
z
x
y
x
x
o
o
x
o
o
υ
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
2
2
2
2
2
2
2
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
1
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
z
v
y
v
x
v
l
v
x
p
ρ
v
ρ
p
X
v
l
g
z
v
v
y
v
v
x
v
v
t
v
t
v
l
x
y
x
o
o
o
o
o
o
o
x
z
x
y
x
x
x
o
o
o
υ
Re
1
,
Eu
1
,
Fr
1
,
St
1
2
2
=
=
=
=
o
o
o
o
o
o
o
o
o
o
l
v
v
ρ
p
v
l
g
t
v
l
υ
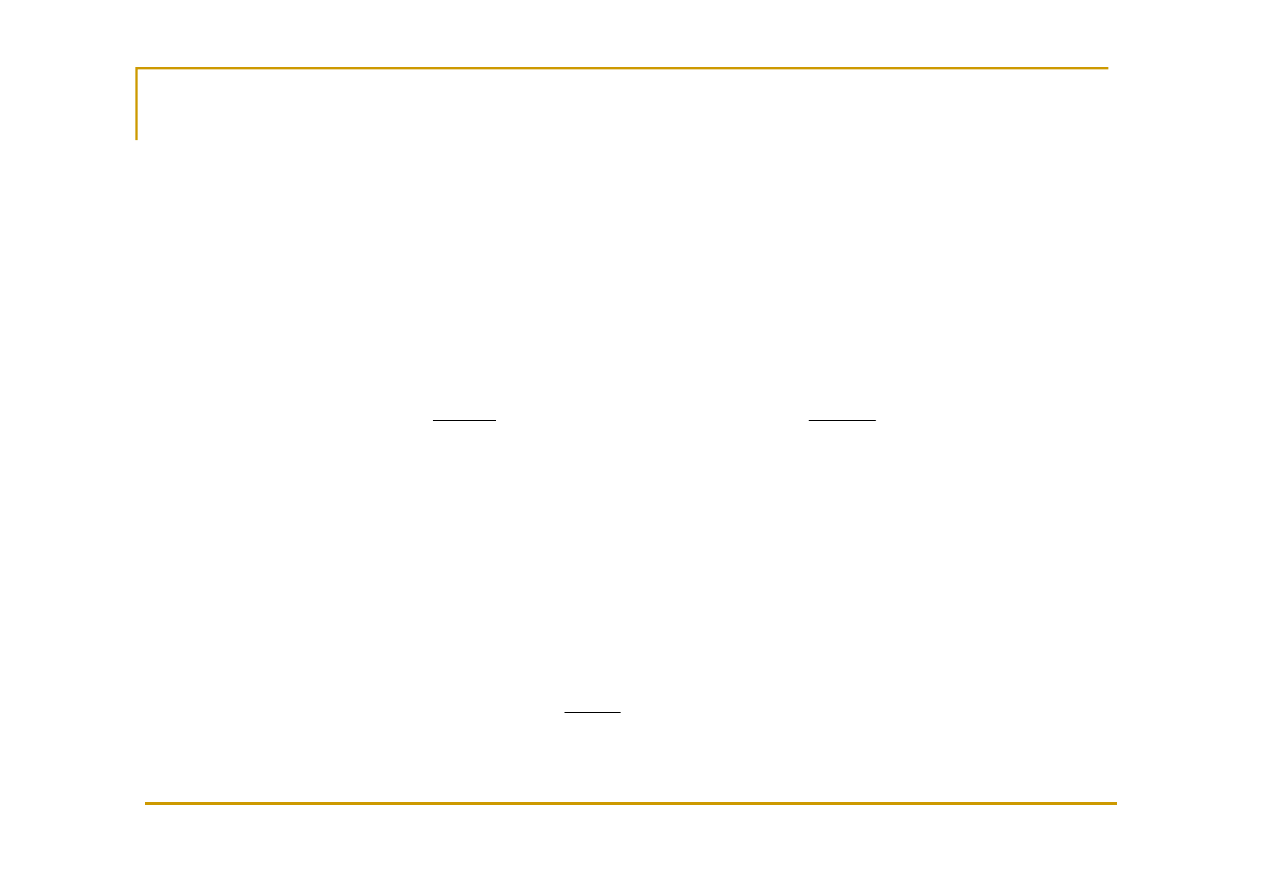
idem
St
=
=
o
o
l
t
v
Liczba Strouhala
- informuje o proporcji sił wynikaj
ą
cych z konwekcyjnych sił
bezwładno
ś
ci do sił powodowanych przez lokalne przyspieszenia.
Odgrywa ona znacz
ą
c
ą
rol
ę
przy badaniu przepływów niestacjonarnych i zwi
ą
zanych
z tym zjawisk, przede wszystkim przepływów pulsacyjnych (np. samowzbudnych drga
ń
konstrukcji w niestacjonarnym opływie, opływ struny, ruch
ś
migła).
Kryteria podobieństwa przepływów
o
o
v
f
l
=
St
o
l
idem
Fr
2
=
=
g
l
v
o
o
Liczba Froude’a
- podaje proporcj
ę
pomi
ę
dzy konwekcyjnymi siłami bezwładno
ś
ci
i siłami grawitacyjnymi. Dotyczy głównie zjawisk ruchu cieczy w ziemskim polu
grawitacyjnym z obecno
ś
ci
ą
swobodnej (pofalowanej) powierzchni cieczy.
Ma ona znaczenie w badaniu modeli okr
ę
tów oraz np. badaniu wiatru w górach.
o
v

Kryteria podobieństwa przepływów
Liczba Eulera
- podaje dla cieczy proporcj
ę
pomi
ę
dzy siłami ci
ś
nienia i konwekcyjnymi
siłami bezwładno
ś
ci, poniewa
ż
dla cieczy g
ę
sto
ść
i ci
ś
nienie s
ą
niezale
ż
ne od siebie.
W budowie maszyn wodnych liczba ta ma zastosowanie przy analizie zjawisk kawitacji.
Liczba Macha
- jest najwa
ż
niejszym kryterium w dynamice gazów.
idem
Eu
2
o
o
=
=
o
v
p
ρ
Liczba Macha
- jest najwa
ż
niejszym kryterium w dynamice gazów.
idem
Ma
1
1
1
Eu
2
2
2
=
=
=
κ
v
a
κ
o
o
idem
Re
=
=
=
µ
ρ
v
l
v
l
o
o
o
o
o
υ
Liczba Reynoldsa -
podaje proporcj
ę
pomi
ę
dzy konwekcyjnymi siłami bezwładno
ś
ci
i siłami lepko
ś
ci. Odgrywa ona kluczow
ą
rol
ę
w badaniu przepływów płynów lepkich.
V
p
o
o
o
c
c
κ
p
κ
a
=
=
,
2
ρ

Kryteria podobieństwa przepływów
Liczba Prandtla
- podaje dla cieczy proporcj
ę
pomi
ę
dzy molekularnym współczynnikiem
dyfuzji p
ę
dy a molekularnym współczynnikiem dyfuzji energii (ciepła).
Odgrywa rol
ę
w procesach konwekcyjnej wymiany ciepła.
Z równania energii w formie bezwymiarowej wynikaj
ą
dwie dodatkowe liczby
podobie
ń
stwa:
idem,
Pr
=
=
=
υ
µ
c
λρ
=
a
a – wsp. wyrównywania temp.
idem,
a
Pr
=
=
=
υ
λ
µ
c
idem
Nu
=
=
λ
α
o
l
Liczba Nusselta -
Odgrywa rol
ę
w opisie zjawisk przejmowania ciepła z płynu przez
ś
ciank
ę
.
c
λρ
=
a
a – wsp. wyrównywania temp.
λ
– wsp. przewodzenia ciepła
c
– ciepło wła
ś
ciwe
α
– wsp. przejmowania ciepła

Twierdzeniem Π (Buckinghama)
Zależności matematyczne pomiędzy wielkościami fizycznymi wyrażające prawa
fizyki nie zależą od wyboru układu jednostek, a wymiar obu stron równań
jest taki sam dla danego układu jednostek
.
Jeśli wśród n wielkości fizycznych opisujących dane zjawisko
jest k wielkości wymiarowo niezależnych, to można utworzyć z nich
(n - k) niezależnych bezwymiarowych iloczynów potęgowych.
Te spośród nich, które są zbudowane z wielkości fizycznych będących stałymi,
są parametrami podobieństwa.

Ustalony przepływ cieczy w rurze chropowatej o przekroju kołowym zale
ż
y od
nast
ę
puj
ą
cych parametrów:
d
− ś
rednicy rury,
v
− ś
redniej pr
ę
dko
ś
ci transportu masy,
ρ
−
g
ę
sto
ś
ci cieczy,
µ
−
lepko
ś
ci dynamicznej cieczy,
∆
p
st
/l
−
spadku ci
ś
nienia (strat tarcia) odniesionego do jednostki jej długo
ś
ci,
k
− ś
redniej chropowato
ś
ci powierzchni wewn
ę
trznej ruroci
ą
gu.
Przepływ w rurze kołowej
0
,
,
,
,
,
st
=
∆
k
l
p
v
d
f
µ
ρ
)
(
)
(
)
(
,
L
M
~
,
T
L
~
,
L
~
3
2
1
3
1
1
1
1
a
a
a
v
d
−
−
ρ
)
(
)
(
)
(
L
~
T
L
M
~
T
L
M
~
6
5
4
1
2
2
1
1
1
1
a
a
a
k
L
p
−
−
−
−
∆
µ

k
ρ
v
d
l
p
ρ
v
d
µ
;
ρ
v
d
z
y
x
z
y
x
z
y
x
3
3
3
2
2
2
1
1
1
3
2
1
Π
;
Π
Π
=
∆
=
=
(
) ( ) (
) (
) (
)
1
1
1
3
1
1
1
1
0
0
0
1
T
L
M
L
M
T
L
L
T
M
L
Π
1
1
1
−
−
−
−
=
=
z
y
x
=
−
−
+
0
1
3
1
1
1
z
y
x
1
µ
Przepływ w rurze kołowej
−
= 1
1
x
=
+
=
+
=
−
−
+
0
1
0
1
0
1
3
1
1
1
1
1
y
z
z
y
x
Re
1
Π
1
1
1
1
=
=
=
−
−
−
ρ
d
v
µ
µ
ρ
v
d
d
k
v
d
l
p
=
∆
=
3
2
st
2
Π
Π
ρ
0
,
,
Re
1
2
st
=
∆
d
k
v
d
L
p
ρ
ϕ
d
L
v
k
d
f
p
2
Re,
2
t
st
=
∆
ρ
−
=
−
=
−
=
1
1
1
1
1
1
z
y
x

Opływ ciała gazem lepkim
Zjawisko opływu ciała (niesmukłego) gazem lepkim zależy od:
d
− charakterystycznego wymiaru tego ciała,
v
− prędkości napływu,
ρ
− gęstości gazu,
w znacznej odległości od ciała
µ − lepkości dynamicznej gazu,
a
− prędkości dźwięku,
F
− siły działającej na to ciało ze strony gazu.
ρ
−
−
)
a
(
,
L
M
~
)
a
(
,
T
L
~
v
)
a
(
,
L
~
d
3
3
1
2
1
1
1
1
)
a
(
T
L
M
~
F
)
a
(
T
L
~
a
)
a
(
T
L
M
~
6
2
1
1
5
1
1
4
1
1
1
−
−
−
−
µ
(
)
0
F
,
a
,
,
v,
,
d
f
=
µ
ρ
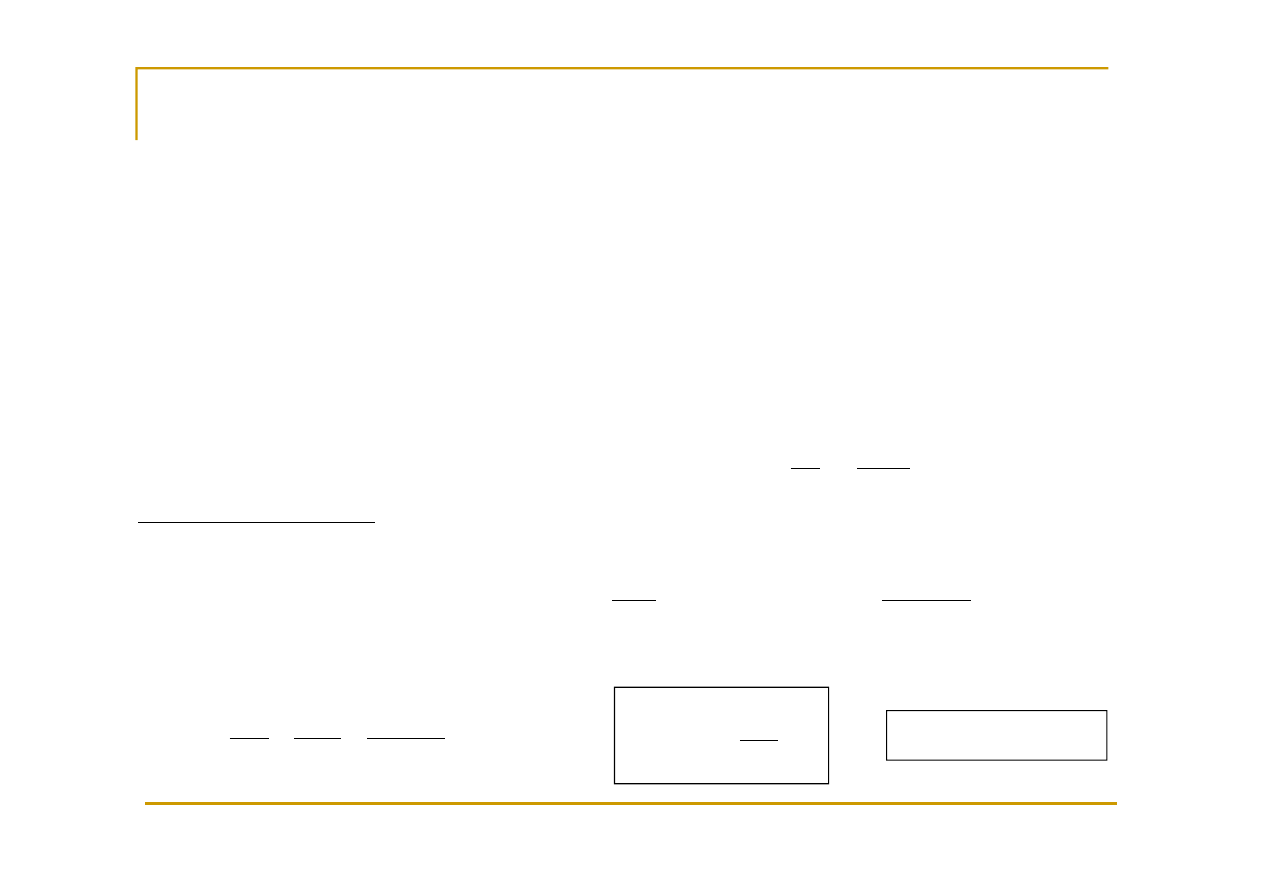
Opływ ciała gazem lepkim
F
v
d
Π
;
a
v
d
Π
;
v
d
Π
3
3
3
2
2
2
1
1
1
z
y
x
3
z
y
x
2
z
y
x
1
ρ
=
⋅
ρ
=
µ
ρ
=
(
) ( ) (
) (
) (
)
1
1
z
3
1
y
1
1
x
1
0
0
0
2
T
L
L
M
T
L
L
T
M
L
Π
2
2
2
−
−
−
=
=
0
z
0
1
z
3
y
x
2
2
2
=
=
+
−
+
1
a
v
d
a
Π
0
1
0
=
=
ρ
=
−
0
z
1
y
0
x
0
1
y
0
z
2
2
2
2
2
=
−
=
=
=
−
−
=
Ma
1
v
a
v
d
a
Π
0
1
0
2
=
=
ρ
=
−
2
2
3
1
d
v
F
Π
;
Re
1
Π
ρ
=
=
0
d
v
F
,
Ma
1
,
Re
1
2
2
=
ρ
ϕ
x
2
x
x
A
2
v
c
F
ρ
=
(
)
Ma
Re,
f
c
x
=
Wyszukiwarka
Podobne podstrony:
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 9
Mechanika płynów dzienne energetyka 30h Wyklad 4
Mechanika płynów dzienne energetyka 30h Wyklad 5
Mechanika płynów dzienne energetyka 30h Wyklad 7
Mechanika płynów dzienne energetyka 30h Wyklad 1
Mechanika płynów dzienne energetyka 30h Wyklad 3
Mechanika płynów dzienne energetyka 30h Wyklad 8
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 10
Mechanika płynów dzienne energetyka 30h Wyklad 3
Mechanika płynów dzienne energetyka 30h Wyklad 9
więcej podobnych podstron