LABORATORIUM WIBROAKUSTYKI MASZYN

Wydział Budowy Maszyn i Zarządzania

Instytut Mechaniki Stosowanej

Zakład Wibroakustyki i Bio-Dynamiki Systemów

Grupa: M2
Imię i Nazwisko:
1.Kukiełczyński Piotr
2.Nowak Rafał

Ć

wiczenie nr. 2 : Wibroizolacja – określanie właściwości wibroizolacyjnych

materiałów

Data wykonania ćwiczenia:
22 listopad 2011

Data oddania sprawozdania:
20 grudzień 2011

Ocena:

1.

Cel ćwiczenia:

•

Ocena właściwości wibroizolacyjnych badanych materiałów.

•

Poznanie układu do badania funkcji wibroizolacji oraz zasad przeprowadzania testu
harmonicznego.

•

Wyznaczenie funkcji wibroizolacji badanego materiału (wibroizolatora) metodą testu
harmonicznego.

•

Wyznaczenie praktycznego zakresu wibroizolacji dla badanego materiału.

2.

Schemat stanowiska:

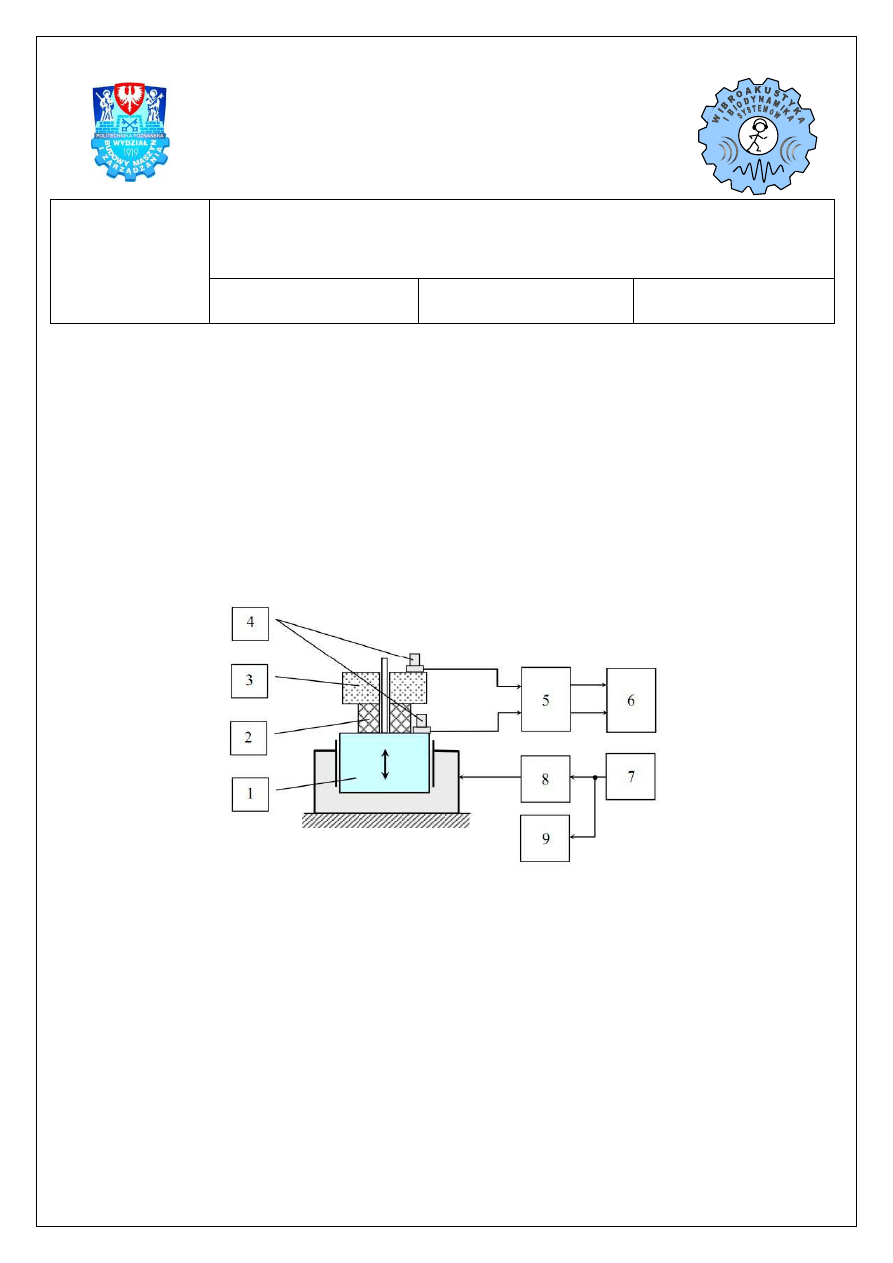
1. Schemat blokowy stanowiska do wyznaczania właściwości wibroizolacyjnych materiałów; 1 – wzbudnik drgań, 2
– badany materiał wibroizolacyjny, 3 – obiekt chroniony (wibroizolowany), 4 – piezoelektryczne przetworniki
drgań, 5 – miernik drgań, 6 – oscyloskop, 7 – generator sygnału harmonicznego, 8 – wzmacniacz mocy, 9 –
częstotliwościomierz

3.

Przebieg ćwiczenia:

W trakcie zajęć zmienialiśmy częstotliwość drgań obiektu chronionego. Dla różnych
częstotliwości odczytywaliśmy z aparatury pomiarowej amplitudy prędkości drgań podłoża w

0

i drgań na obiekcie wibroizolowany v

0

. Następnie obliczaliśmy stosunek v

0

/w

0

.

4.

Wyniki pomiarów:

Lp

Częstotliwość

f [Hz]

Amplituda prędkości

drgań podłoża w

0

[m/s]

Amplituda prędkości

drgań na obiekcie

wibroizolowanym v

0

[m/s]

Stosunek drgań na

obiekcie do drgań na

podłożu v

0

/w

0

1

3,4

0,400

0,300

0,75

2

8,2

0,320

0,300

0,94

3

14,1

0,210

0,220

1,05

4

18,9

0,220

0,260

1,18

5

25,6

0,150

0,210

1,40

6

31,3

0,112

0,160

1,43

7

36,0

0,080

0,144

1,80

8

40,5

0,050

0,123

2,46

9

45,9

0,032

0,114

3,56

10

51,5

0,013

0,104

8,00

11

52,3

0,013

0,106

8,15

12

53,4

0,014

0,106

7,57

13

54,1

0,015

0,108

7,20

14

54,9

0,017

0,108

6,35

15

55,5

0,019

0,114

6,00

16

56,7

0,023

0,106

4,61

17

59,8

0,034

0,109

3,21

18

61,0

0,037

0,110

2,97

19

63,5

0,061

0,116

1,90

20

69,2

0,096

0,125

1,30

21

71,3

0,100

0,126

1,26

22

74,8

0,132

0,126

0,95

23

79,9

0,150

0,108

0,72

24

86,0

0,145

0,080

0,55

25

92,1

0,132

0,050

0,38

26

102,3

0,101

0,040

0,40

27

104,1

0,098

0,030

0,31

0,00

1,00

2,00

3,00

4,00

5,00

6,00

7,00

8,00

9,00

0

50

100

150

W

ib

ro

iz

o

la

cj

a

K

Częstotliwość [Hz]

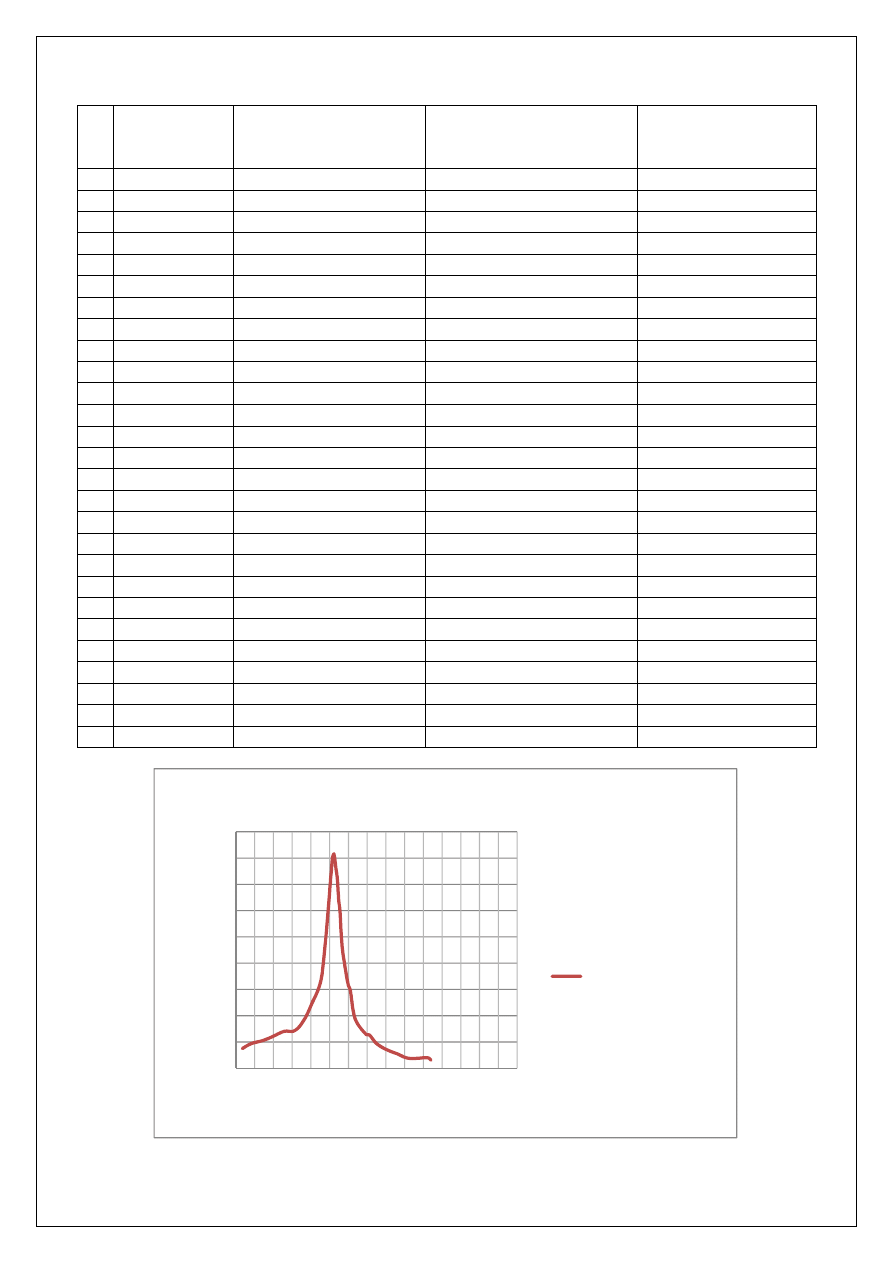
Funkcja wibroizolacji K(f)

Funkcja wibroizolacji K

5.

Obliczenia:

Odczytane z wykresu:

A

max

=8,15

√2

= 5,76

= 52,3

= 44,3

= 47,9

= − =

1

2 → =

−

2

Q – dobroć układu mechanicznego;
ξ – stopień tłumienia.

=

47,9 − 44,3

52,3

= 0,07

Teoretyczna funkcja wibroizolacji przedstawia się wzorem:

"# $ = %

1 + 4 ' (

)1 − ' ( * + 4 ' (

0,00

1,00

2,00

3,00

4,00

5,00

6,00

7,00

8,00

0

20

40

60

80

100

120

W

ib

ro

iz

o

la

cj

a

K

Częstotliwość [Hz]

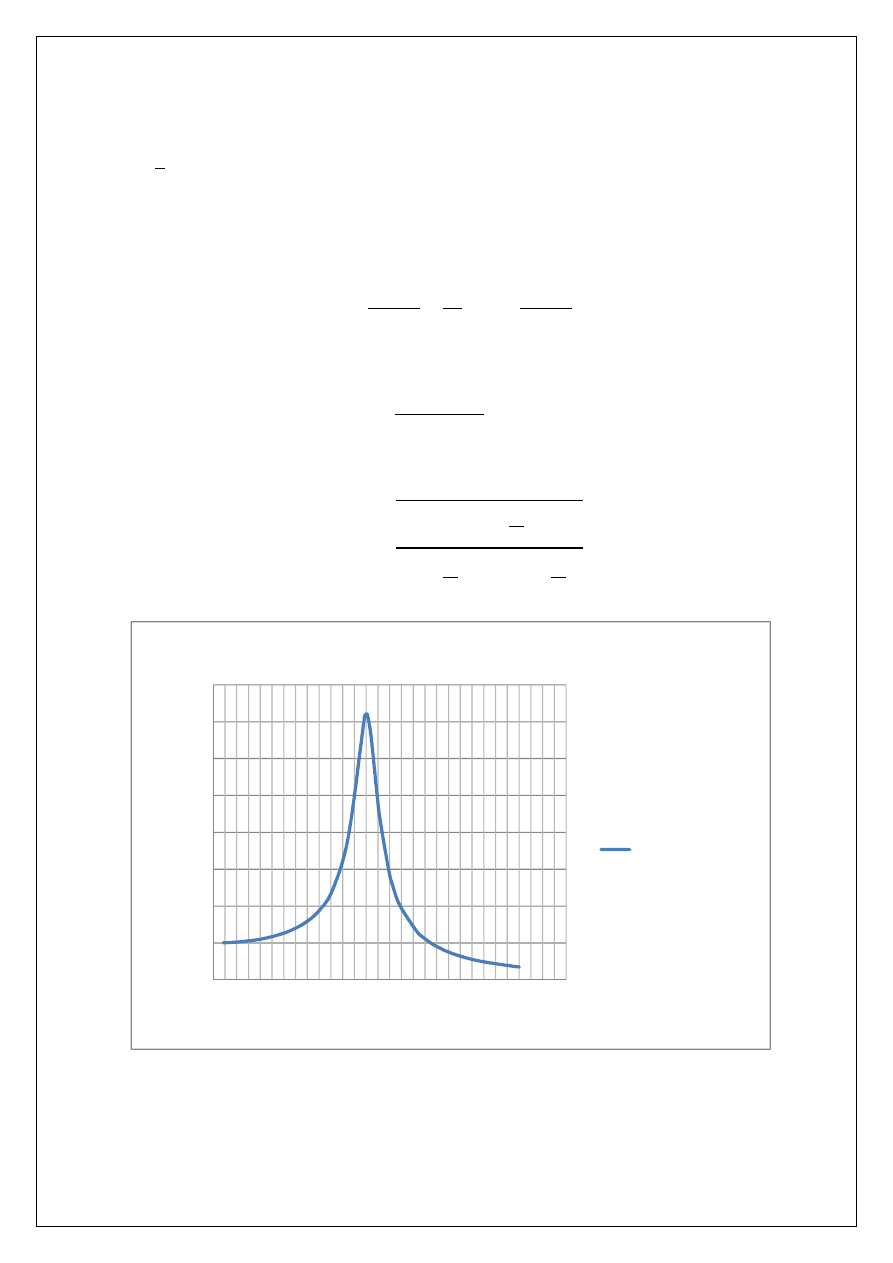
Teoretyczna funkcja wibroizolacji K(f)

Teoretyczna funkcja
wibroizolacji

6.

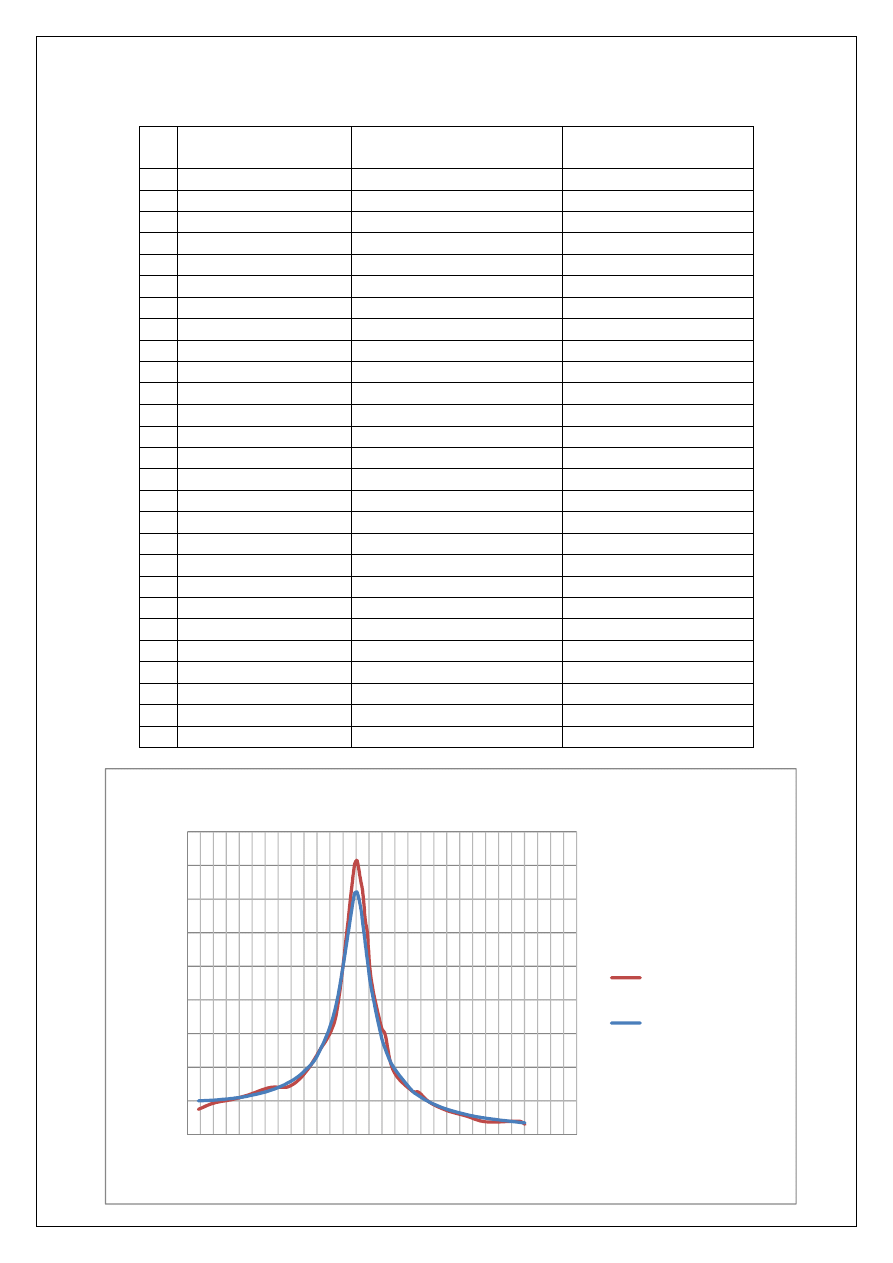
Zestawienie wyników, wykresy kolumnowe, punktowe itp. najbardziej adekwatne do

uzyskanych wyników:

Lp Częstotliwość f [Hz]

Wartości doświadczalnej

funkcji wibroizolacji

Wartości teoretycznej

funkcji wibroizolacji

1

3,4

0,75

1,00

2

8,2

0,94

1,03

3

14,1

1,05

1,08

4

18,9

1,18

1,15

5

25,6

1,40

1,31

6

31,3

1,43

1,55

7

36,0

1,80

1,88

8

40,5

2,46

2,43

9

45,9

3,56

3,87

10

51,5

8,00

7,15

11

52,3

8,15

7,21

12

53,4

7,57

6,77

13

54,1

7,20

6,28

14

54,9

6,35

5,65

15

55,5

6,00

5,19

16

56,7

4,61

4,36

17

59,8

3,21

2,92

18

61,0

2,97

2,56

19

63,5

1,90

2,01

20

69,2

1,30

1,32

21

71,3

1,26

1,16

22

74,8

0,95

0,96

23

79,9

0,72

0,76

24

86,0

0,55

0,60

25

92,1

0,38

0,49

26

102,3

0,40

0,37

27

104,1

0,31

0,35

0,00

1,00

2,00

3,00

4,00

5,00

6,00

7,00

8,00

9,00

0

20

40

60

80

100

120

W

ib

ro

iz

o

la

cj

a

K

Częstotliwość [Hz]

Funkcja wibroizolacji K(f)

Funkcja wibroizolacji K

Teoretyczna funkcja
wibroizolacji

7.

Wnioski, podsumowanie:

•

Doświadczalna funkcja wibroizolacji jest bardziej postrzępiona niż doświadczalna. Wynika
to z faktu, że do uzyskanych wyników mogły się wkraść pewne błędy odczytu. Ponadto
teoria zakłada przypadki idealne. Środowisko zewnętrzne również mogło mieć wpływ na
uzyskane wyniki.
Z tego samego powodu szczyt doświadczalnej funkcji wibroizolacji K(f) znajduje się wyżej
niż dla funkcji teoretycznej.

•

Zakres częstotliwości, w którym funkcja osiąga wartość maksymalną jest obszarem
rezonansu układu mechanicznego.

•

Obszar praktycznej wibroizolacji przyjmuje się dla δ>3 (bezwymiarowa częstość
wymuszenia), gdzie K<<1. Wynika to z faktu, że amplituda drgań chronionego obiektu
powinna być znacznie mniejsza od amplitudy drgań podłoża.