Szeregi liczbowe

Zdefiniujmy w przestrzeni wektorowej pewną operację na ciągach, która jest uogólnieniem
operacji sumowania ciągów skończonych.

Niech

 X ,

∥

⋅

∥

 - przestrzeń unormowana

a

n



n

∈ℕ

- ciąg elementów z X

Definicja

Szeregiem

o wyrazie ogólnym a

n

nazywamy ciąg S

n



n

∈ℕ

, gdzie S

n

:

=

∑

k

=1

n

a

k

,

i oznaczamy ten ciąg symbolem

∑

k

=1

∞

a

k

. Element S

n

nazywamy

n-tą sumą

cząstkową

szeregu

∑

k

=1

∞

a

k

.

Definicja

Szereg nazywamy

zbieżnym

, jeśli ciąg S

n



n

∈ℕ

jest zbieżny do elementu przestrzeni X .

Element ten, czyli lim

n

∞

S

n

nazywamy

sumą

szeregu

∑

k

=1

∞

a

k

i oznaczamy również tym

samym symbolem

∑

k

=1

∞

a

k

.

Definicja

Szereg, który nie jest zbieżny nazywamy

rozbieżnym

.

Uwaga

Symbol

∑

k

=1

∞

a

k

ma dwa znaczenia:

●

∑

k

=1

∞

a

k

=S

n



n

∈ℕ

●

∑

k

=1

∞

a

k

=

∃ lim

n

∞

S

n

lim

n

∞

S

n

=: S

- 1 -

Przykłady

1)

∑

n

=0

∞

q

n

-

szereg geometryczny, q ≠ 1, q

∈ℂ

Wtedy

S

n

=

∑

k

=0

n

q

k

=

1

−q

n

1

1

−q

∑

n

=0

∞

q

n

- zbieżny

⇔ ∃ lim

n

∞

S

n

Aby istniała granica musi zachodzić |q|<1 i wtedy lim

n

∞

1

−q

n

1

1

−q

=

1

1

−q

Stąd

∑

n

=0

∞

q

n

=

1

1

−q

dla |q|<1.

2)

∑

n

=1

∞

1

n

n1

S

n

=

∑

k

=1

n

1

k

k1

=

∑

k

=1

n



1
k

−

1

k

1

=1−

1

2



1
2

−

1
3



1
3

−

1

4

...

1

n

−1

−

1

n



1

n

−

1

n

1

=1−

1

n

1

lim

n

∞

S

n

=lim

n

∞

1−

1

n

1

=1

⇒

szereg

∑

n

=1

∞

1

n

n1 jest zbieżny i

∑

n

=1

∞

1

n

n1

=1

W przestrzeni Banacha ciąg jest zbieżny

⇔ jest ciągiem Cauchy'ego, stąd wynika

następujące twierdzenie:

Twierdzenie

(WKW zbieżności Cauchy'ego)

Niech (X, ||.||)- przestrzeń Banacha
i niech a

k

∈ X dla k ∈ℕ.

Wtedy

∑

k

=1

∞

a

k

−zbieżny ⇔ ∀ 0 ∃n

0

∈ℕ ∀ n , m∈ ℕ , n

0

m≤n

∥

∑

k

=m

n

a

k

∥



Dowód

∑

k

=1

∞

a

k

- zbieżny

⇔ S

n



n

∈ℕ

- zbieżny

⇔ S

n



n

∈ℕ

- ciąg Cauchy'ego

⇔

⇔ ∀ 0 ∃n

0

∈ℕ ∀ n , m∈ ℕ, n

0

m−1≤n

∥

S

n

−S

m

−1

∥





- 2 -

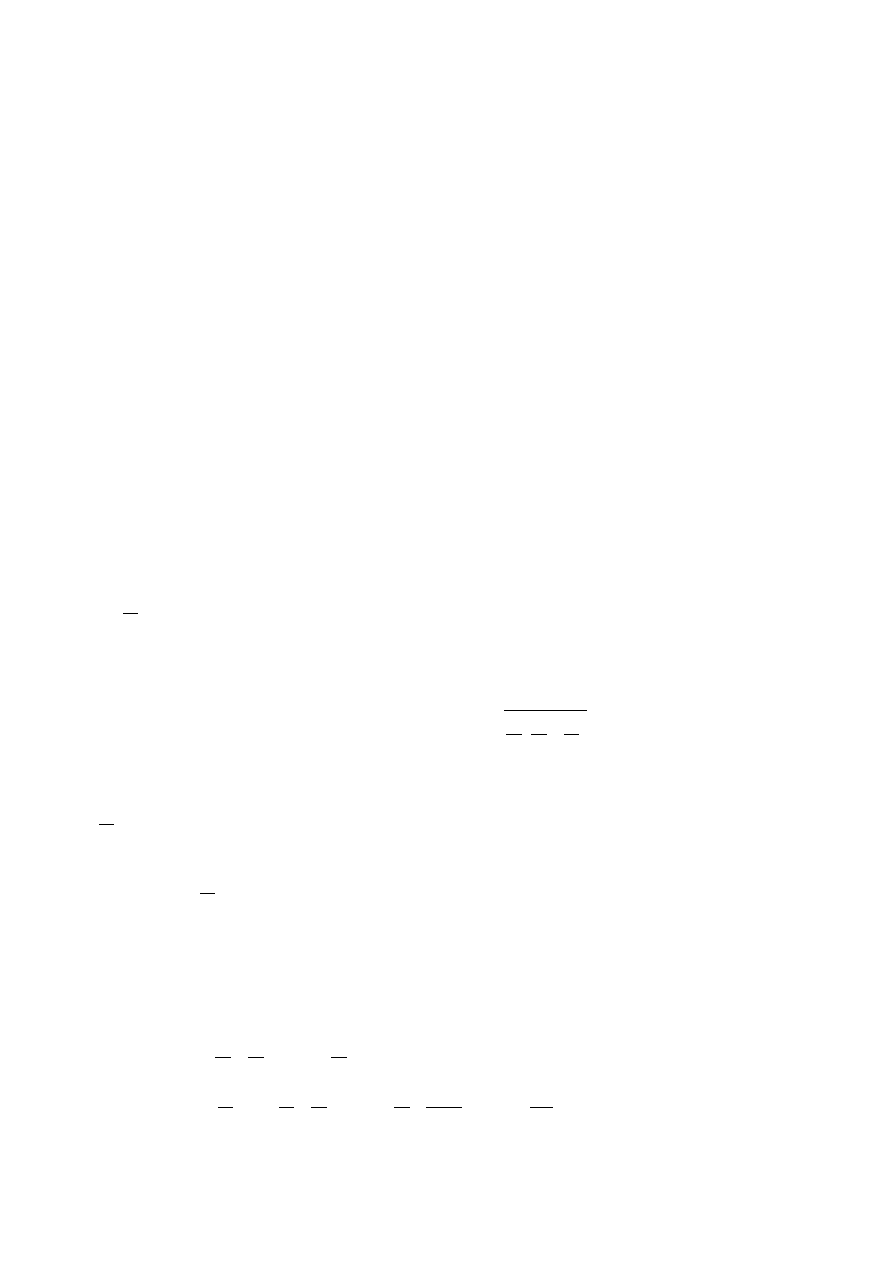
Twierdzenie

(WK zbieżności szeregu)

∑

n

=1

∞

a

n

−zbieżny ⇒ lim

n

∞

a

n

=0

Dowód

∑

n

=1

∞

a

n

−zbieżny ⇒ ∃ lim

n

 ∞

S

n

=S ⇒ ∃ lim

n

 ∞

S

n

−1

=S

Ponieważ

S

n

=S

n

−1

a

n

dla n

≥2

zatem

lim

n

∞

a

n

=lim

n

∞

S

n

−S

n

−1

=S−S=0



Uwaga

Warunek lim

n

∞

a

n

=0 nie jest warunkiem wystarczającym zbieżności szeregu.

Przykład

∑

n

=1

∞

1

n

-

szereg harmoniczny

Nazwa pochodzi od średniej harmonicznej liczb, bo a

n

jest średnią

harmoniczną

a

n

−1

i a

n

1

, gdzie

średnia harmoniczba liczb a i b jest to

1

1
2



1

a



1

b



(odwrotność

połowy sumy odwrotności tych liczb).

1

n



n

∞

0

⇒ WK zbieżności szeregu zachodzi, jednak szereg jest rozbieżny.

Hipoteza:

∑

n

=1

∞

1

n

- zbieżny.

Wtedy

∃ lim

n

∞

S

n

=S ∈ℝ

S

2 n



n

∈ℕ

− podciąg ciągu S

n



n

∈ℕ

}

⇒ lim

n

∞

S

2 n

=S ⇒ lim

n

∞

S

2 n

−S

n

=S−S=0

Z drugiej strony

S

n

=

∑

k

=1

n

a

k

=1 

1
2



1
3

. . .

1

n

S

2 n

=

∑

k

=1

2 n

a

k

=

∑

k

=1

2 n

1

k

=1 

1

2



1
3

. . .

1

n



1

n

1

. . .

1

2 n

- 3 -

Zatem

S

2 n

−S

n

=

1

n

1



1

n

2

. . .

1

2 n



n

≥n

1

2 n

=

1

2

⇒ lim

n

∞

S

2 n

−S

n

≥

1
2

- sprzeczność
(hipoteza fałszywa)

⇩

∑

n

=1

∞

1

n

- szereg rozbieżny

Definicja

Szereg

∑

n

=1

∞

a

n

nazywamy

bezwzględnie zbieżnym

, gdy zbieżny jest szereg norm

∑

n

=1

∞

∣∣a

n

∣∣.

Szereg

∑

n

=1

∞

a

n

nazywamy

warunkowo zbieżnym

, gdy jest zbieżny lecz nie bezwzględnie.

Twierdzenie

(o szeregu zbieżnym bezwzględnie)

Niech (X, ||.||) - przestrzeń Banacha nad ciałem K.

Jeśli

∑

n

=1

∞

a

n

- jest zbieżny bezwzględnie

⇒

1)

∑

n

=1

∞

a

n

- zbieżny

2)

∥

∑

n

=1

∞

a

n

∥

≤

∑

n

=1

∞

∥

a

n

∥

Dowód w oparciu o WKW Cauchy'ego.

Twierdzenie

(działania na szeregach)

Niech A

∈ K.

Jeżeli szeregi wektorowe

∑

n

=1

∞

a

n

,

∑

n

=1

∞

b

n

są zbieżne, to szeregi

∑

n

=1

∞

a

n

b

n

 i

∑

n

=1

∞

A a

n

są zbieżne i zachodzi

1)

∑

n

=1

∞

a

n

b

n

=

∑

n

=1

∞

a

n



∑

n

=1

∞

b

n

2)

∑

n

=1

∞

Aa

n

=A

∑

n

=1

∞

a

n

- 4 -

Twierdzenie

(Cauchy'ego o iloczynie szeregów)

Jeżeli szeregi liczbowe

∑

n

=0

∞

a

n

,

∑

n

=0

∞

b

n

są zbieżne bezwzględnie, to szereg

∑

n

=0

∞

c

n

,

gdzie c

n

:

=

∑

k

=0

n

a

k

b

n

−k

dla n

∈ℕ

0

, jest zbieżny bezwzględnie i zachodzi

∑

n

=0

∞

c

n

=



∑

n

=0

∞

a

n



⋅



∑

n

=0

∞

b

n



Szereg

∑

n

=0

∞

c

n

nazywamy

iloczynem Cauchy'ego

szeregów

∑

n

=0

∞

a

n

i

∑

n

=0

∞

b

n

.

Kryteria zbieżności szeregów liczbowych

Na podstawie twierdzenia o szeregu zbieżnym bezwzględnym, każdy szereg zbieżny
bezwzględnie jest zbieżny, zatem istotne są kryteria zbieżności bezwzględnej, czyli
kryteria zbieżności szeregów o wyrazach nieujemnych.

Uwaga

Niech p

∈ℕ. Wtedy

∑

n

=1

∞

a

n

− zbieżny ⇔

∑

n

= p

∞

a

n

−zbieżny

Dowód

S

n

=a

1

a

2

. . .a

n

=a

1

a

2

. . .a

p

−1



const

a

p

a

p

1

. . .a

n



S

n

'

dla n

≥ p

S

n

=constS

n

'

∃ lim

n

∞

S

n

⇔ ∃ lim

n

∞

S

n

'



Twierdzenie

(kryterium porównawcze - wersja klasyczna)

Niech p

∈ℕ

oraz niech 0

≤a

n

≤b

n

dla n

≥ p .

Wtedy

1) Jeśli

∑

n

=1

∞

b

n

- zbieżny, to

∑

n

=1

∞

a

n

- zbieżny

2) Jeśli

∑

n

=1

∞

a

n

- rozbieżny, to

∑

n

=1

∞

b

n

- rozbieżny

- 5 -

Dowód

Ad. (1). Wystarczy zbadać zbieżność szeregów

∑

n

= p

∞

a

n

i

∑

n

= p

∞

b

n

.

Ponieważ ∀ n≥ p 0≤a

n

≤b

n

⇒

∑

k

= p

n

a

k



s

n

≤

∑

k

= p

n

b

k



S

n

zatem dla

s

n

:

=

∑

k

= p

n

a

k

, S

n

:

=

∑

k

= p

n

b

k

, mamy s

n

≤S

n

dla n

≥ p.

Ponadto

s

n



n

∈ℕ

∈↗

oraz S

n



n

∈ℕ

∈↗.

⇩ s

n

≤S

n

 s

n



n

∈ℕ

- ograniczony

s

n



n

∈ℕ

∈↗

s

n



n

∈ℕ

−ograniczony

}

⇒  s

n



n

∈ℕ

−zbieżny ⇒

∑

n

= p

∞

a

n

− zbieżny

Ad. (2).
Implikacja w (2) jest kontrapozycją implikacji w (1).
[p q]

⇒ ⇔ [(~q) (~p)]

⇒

← kontrapozycja implikacji p q

⇒



Uwaga

Jeśli ∀ n≥ p 0≤a

n

≤b

n

, to

1) szereg

∑

n

=1

∞

b

n

nazywamy

majorantą

szeregu

∑

n

=1

∞

a

n

2) szereg

∑

n

=1

∞

a

n

nazywamy

minorantą

szeregu

∑

n

=1

∞

b

n

Zatem kryterium porównawcze można wypowiedzieć:

Kryterium porównawcze

1) Jeśli szereg (o wyrazach nieujemnych) ma majorantę zbieżną, to jest zbieżny.
2) Jeśli szereg (o wyrazach nieujemnych) ma minorantę rozbieżną, to jest rozbieżny.

- 6 -

Ponieważ

∑

n

=1

∞

b

n

− zbieżny ⇒ ∃ lim

n

∞

S

n

⇒ S

n



n

∈ℕ

- ciąg ograniczony

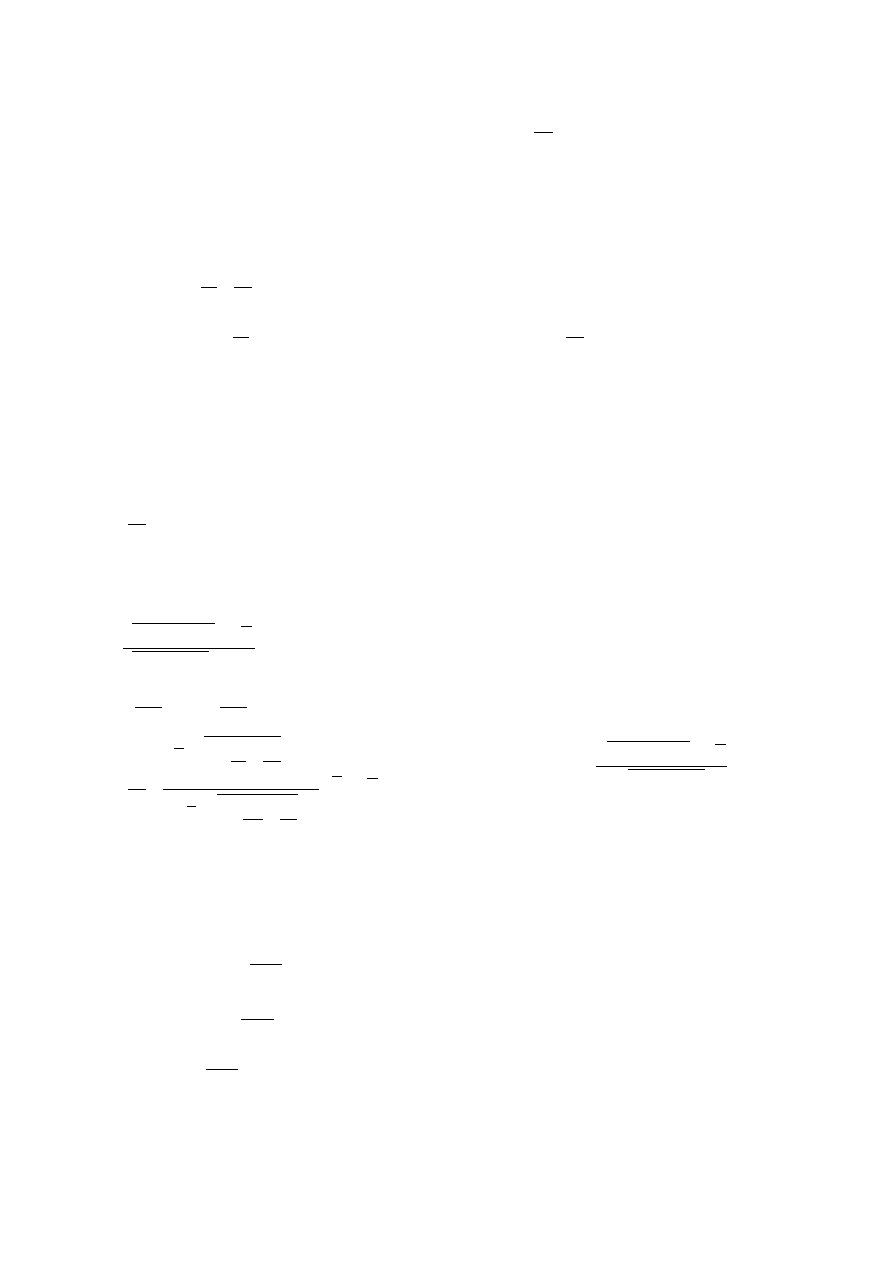
Przykład

Szereg Dirchleta

(uogólniony szereg harmoniczny):

∑

n

=1

∞

1

n



, gdzie

∈ℝ

1)

>1⇒ jest zbieżny

2)

≤1⇒ jest rozbieżny



Dla =1 wykazaliśmy wcześniej, że szereg jest rozbieżny.

Jeśli

<1, to

1

n

≤

1

n



∀ n∈ℕ.

Zatem szereg

∑

n

=1

∞

1

n

jest rozbieżną minorantą szeregu

∑

n

=1

∞

1

n



⇒ szereg Dirchleta dla 1

jest rozbieżny. Zbieżność szeregu Dirchleta dla

>1 wykażemy później, korzystając z

kryterium całkowego.

Twierdzenie

(kryterium porównawcze - wersja graniczna)

∀ n∈ℕ a

n

0, b

n

0

lim

n

∞

a

n

b

n

=K ∈0;∞

}

⇒

∑

n

=1

∞

a

n

i

∑

n

=1

∞

b

n

−są jednocześnie zbieżne

lub jednocześnie rozbieżne

Przykład

∑

n

=1

∞ 9



2 n

3

n

2

n

3



n

6



n

3

2 n−2

b

n

=

1

n

1

/6

∑

n

=1

∞

1

n

1

/6

−szereg Dirchleta rozbieżny

lim

n

∞

a

n

b

n

=

n

1

3



9



2



1

n



1

n

2

1



n

1

2



6



1



2

n

2

−

2

n

3



n

1

6

=

9



2

1 ∈0;∞

}

Twierdzenie

(kryterium d'Alemberta)

Niech a

n

0 .

1) Jeśli lim sup

n

∞

a

n

1

a

n

1, to

∑

n

=1

∞

a

n

jest zbieżny.

2) Jeśli lim sup

n

∞

a

n

1

a

n

1

lub jeśli

a

n

1

a

n

≥1 dla n≥n

0

, n

0

∈ℕ

}

⇒

∑

n

=1

∞

a

n

−rozbieżny

- 7 -

⇒

∑

n

=1

∞

9



2 n

3

n

2

n

3



n

6



n

3

2 n−2

− jest

rozbieżny

Uwaga

W pozostałych przypadkach kryterium nie rozstrzyga o zbieżności.

Dowód

ad.1)

Oznaczmy A:

=lim sup

n

∞

a

n

1

a

n

. Zatem A

1.

Niech

0 i A1.

Ponieważ A jest granicą górną ciągu

a

n

1

a

n

, więc prawie wszystkie wyrazy tego ciągu

będą mniejsze od A

=: q , tzn.

∃n

0

∈ℕ ∀ n≥n

0

a

n

1

a

n

q , gdzie q∈0;1.

Stąd

a

n

1

q a

n

q

2

a

n

−1

q

n

1−n

0

a

n

0

dla n

≥n

0

czyli

a

n

1

q

n

1−n

0

a

n

0

dla n

≥n

0

.

szeregu

∑

n

=n

0

∞

a

n

.

Na podstawie kryterium porównawczego szereg

∑

n

=1

∞

a

n

jest zbieżny.

ad. 2)

I. W przypadku, gdy lim inf

n

∞

a

n

1

a

n

1 , oznaczamy A:=lim inf

n

∞

a

n

1

a

n

.

Zatem A>1. Niech

0

i

q := A

−1.

- 8 -

Szereg

∑

n

=1

∞

q

n

1−n

0

a

n

0

=q

1

−n

0

a

n

0



stałe

⋅

∑

n

=n

0

∞

q

n

jest zbieżny, zatem stanowi zbieżną majorantę



A

q

1



1

A

q

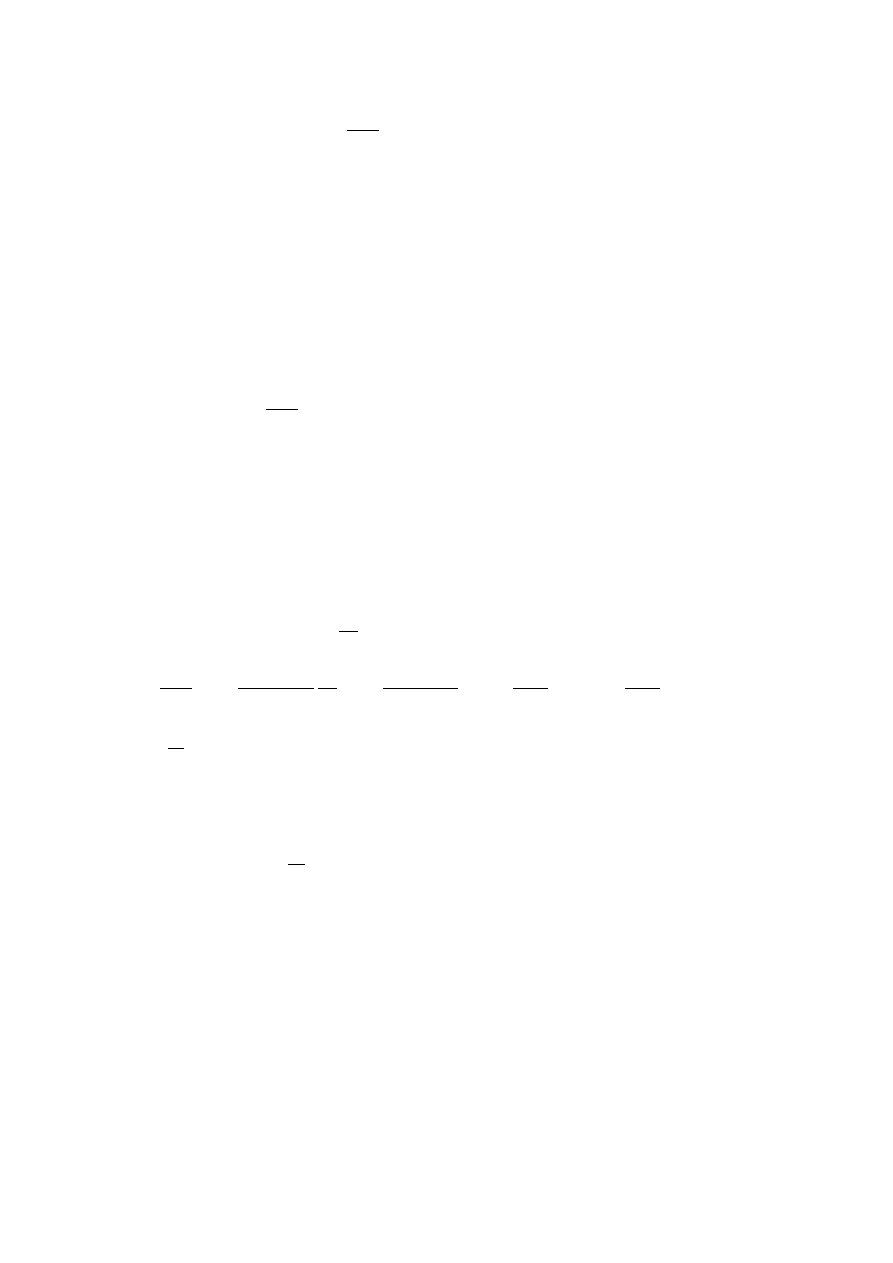
Wtedy

∃n

0

∈ℕ ∀ n≥n

0

a

n

1

a

n

q, gdzie q1.

Stąd

a

n

1

q a

n

q

2

a

n

−1

q

n

1−n

0

a

n

0

dla n

≥n

0

czyli

a

n

1

q

n

1−n

0

a

n

0

.

porównawczego szereg

∑

n

=1

∞

a

n

jest rozbieżny.

II. W przypadku, gdy

a

n

1

a

n

≥1 dla n≥n

0

mamy

a

n

1

≥a

n

≥a

n

−1

≥≥a

n

0

.

Stąd lim

n

∞

a

n

≥a

n

0

0 , czyli nie jest spełniony warunek konieczny zbieżności szeregu, bo

granica lim

n

∞

a

n

≠0 . Zatem

∑

n

=1

∞

a

n

jest rozbieżny.



Przykład

Zbadać zbieżność szeregu

∑

n

=1

∞

n !

n

n

.

lim sup

n

∞

a

n

1

a

n

=lim

n

∞

n1!
n1

n1

n

n

n !

=lim

n

∞

n1n

n

n1

n1

=lim

n

 ∞



n
n

1



n

=lim

n

∞





n

1

n



n



−1

=

lim

n

∞





1



1

n



n



−1

=e

−1

1 ⇒ szereg jest zbieżny na podstawie kryterium d'Alemberta

Twierdzenie

(kryterium Cauchy'ego)

Niech a

n

0, dla n∈ℕ

oraz niech g :=lim sup

n

∞

n



a

n

.

1) Jeśli g

1 , to

∑

n

=1

∞

a

n

- zbieżny

2) Jeśli g

1 , to

∑

n

=1

∞

a

n

- rozbieżny

Uwaga

Kryterium nie rozstrzyga o zbieżności, gdy g

=1 .

- 9 -

Szereg

∑

n

=1

∞

q

n

1−n

0

a

n

0

=q

1

−n

0

a

n

0



stałe

⋅

∑

n

=n

0

∞

q

n

jest rozbieżny, zatem na podstawie kryterium

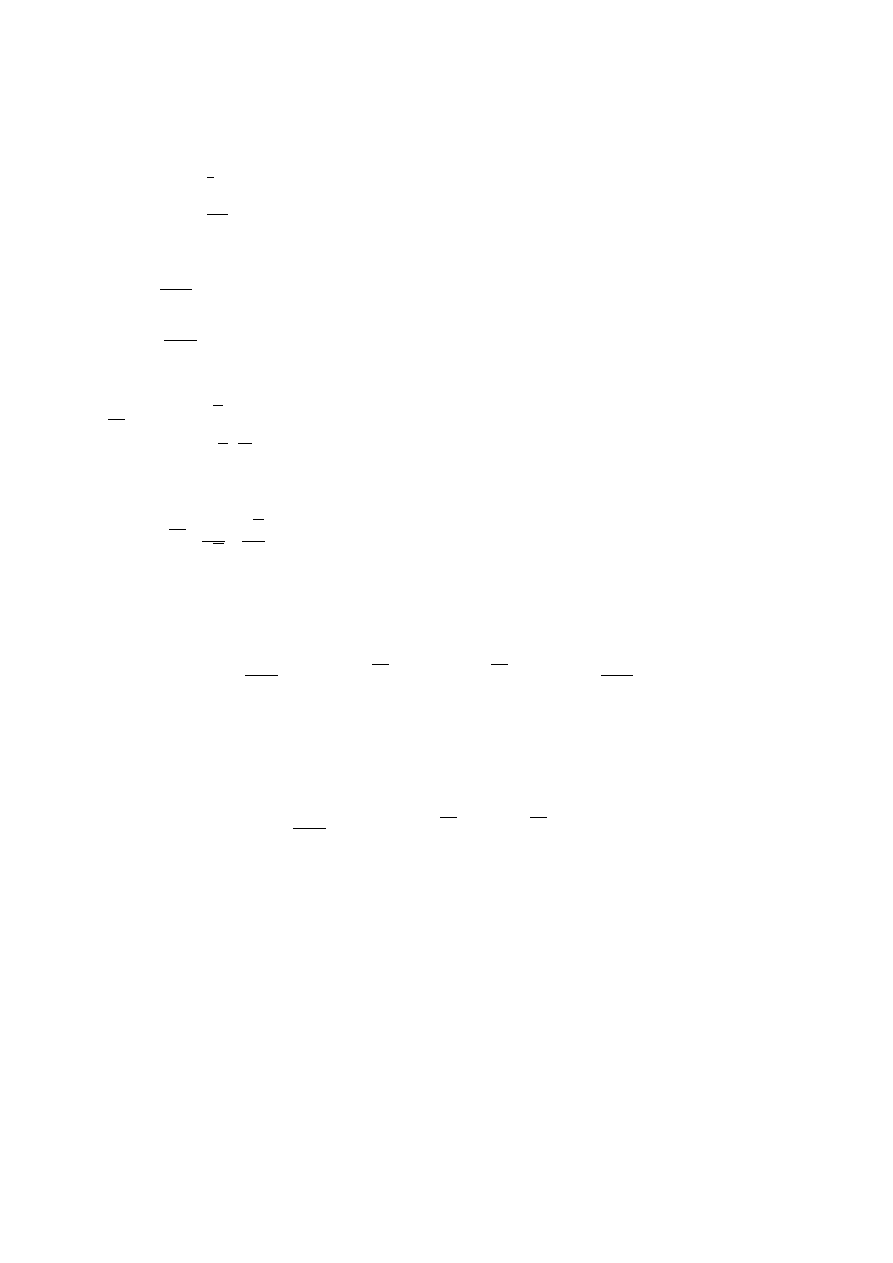
Przykład

Rozważmy

∑

n

=1

∞

a

n

, gdzie

a

n

=

{

2

−

n
2

, gdy n - parzyste

3

−

n

1

2

, gdy n - nieparzyste

Wtedy

lim sup

n

∞

a

n

1

a

n

=∞

lim inf

n

∞

a

n

1

a

n

=0

}

⇒ kryterium d'Alemberta nie rozstrzyga o zbieżności tego

szeregu

Ponadto

n



a

n

=

{

2

−

1
2

, gdy n - parzyste

3

−



1
2



1

2 n



, gdy n - nieparzyste

stąd

lim sup

n

∞

n



a

n

=

1



2

=



2

2

1

⇒

kryt. Cauchy'ego

∑

n

=1

∞

a

n

−zbieżny.

Twierdzenie

Niech a

n

0 dla n∈ℕ . Wtedy

lim inf

n

∞

a

n

1

a

n

≤ lim inf

n

∞

n



a

n

≤ lim sup

n

∞

n



a

n

≤ lim sup

n

∞

a

n

1

a

n

.

Wniosek

1) Jeśli kryterium Cauchy'ego nie rozstrzyga o zbieżności szeregu, to kryterium

d'Alemberta też nie rozstrzyga o zbieżności tego szeregu.

2) Jeśli

∃ granica lim

n

∞

a

n

1

a

n

=g ⇒ ∃ lim

n

∞

n



a

n

∧ lim

n

∞

n



a

n

=g

Twierdzenie

(kryterium całkowe)

Niech dany będzie szereg

∑

n

=n

0

∞

a

n

,

gdzie a

n

0 dla n∈ℕ.

Niech f :[ n

0

;

∞) ℝ

+

f

∈C ([ n

0

;

∞))

f

∈↘

oraz niech a

n

= f n dla n≥n

0

.

}

⇒



∑

n

=n

0

∞

a

n

− zbieżny ⇔

∫

n

0

∞

f

 xdx− zbieżna



- 10 -

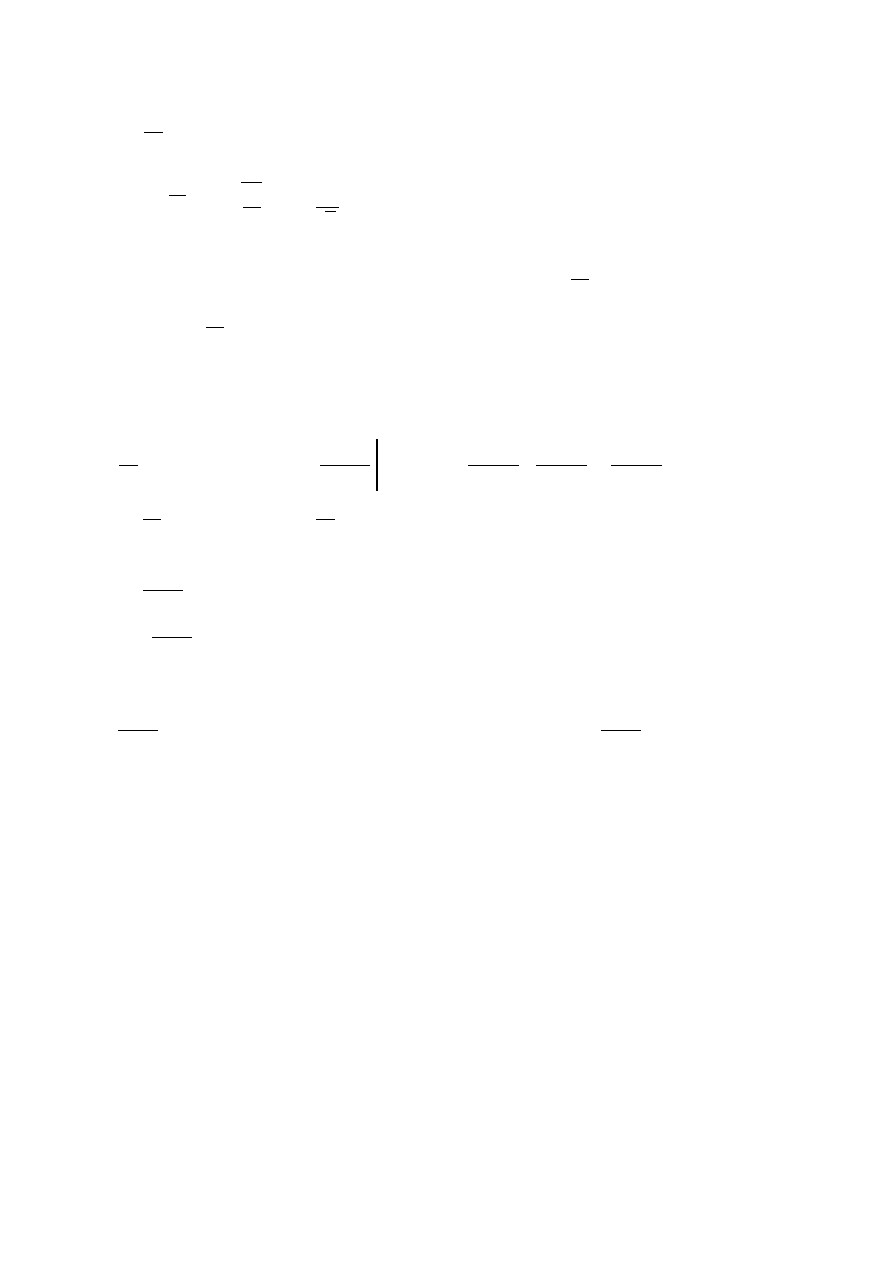
Przykłady

1)

∑

n

=1

∞

1

n



,

1

lim sup

n

∞

n



a

n

=lim

n

∞

n



1

n



=lim

n

∞



1

n



n





=1 ⇒ kryterium Cauchy'ego nie roztrzyga o zbieżności

szeregu (zatem kryterium d'Alemberta też nie rozstrzyga)

Tworzymy funkcję ciągłą f :[ 1;

∞) ℝ

+

taką, aby f

n=

1

n



.

Niech f

 x=

1

x



dla x

∈[ 1 ;∞).

Wtedy
f

∈C ([ 1;∞))

f

∈↘

oraz

∫

1

∞

1

x



dx

= lim

A

∞

∫

1

A

x

−

dx

= lim

A

∞

x

−1

−1

1

A

= lim

A

∞



A

−1

−1

−

1

−1



=

1

−1

⇒

∫

1

∞

1
x



dx

−zbieżna ⇒

∑

n

=1

∞

1

n



−zbieżny

Szereg naprzemienny

Niech a

n

0 dla n∈ℕ.

Szereg

∑

n

=1

∞

−1

n

a

n

nazywamy

szeregiem naprzemiennym

.

Twierdzenie

(kryterium Leibniza)

Niech a

n

0 dla n∈ℕ ,

a

n



n

∈ℕ

∈↘

lim

n

∞

a

n

=0

}

⇒

∑

n

=1

∞

−1

n

a

n

− zbieżny

- 11 -

2)

∑

n

=2

∞

1

n ln n

f

 x=

1

x ln x

, x

≥2

f

∈C ([ 2;∞))

f

∈↘

∫

2

∞

1

x ln x

dx

= lim

A

∞

ln

ln x∣

2

A

=∞ ⇒

∫

2

∞

f

 xdx−rozbieżna ⇒

∑

n

=2

∞

1

nln n

−rozbieżny

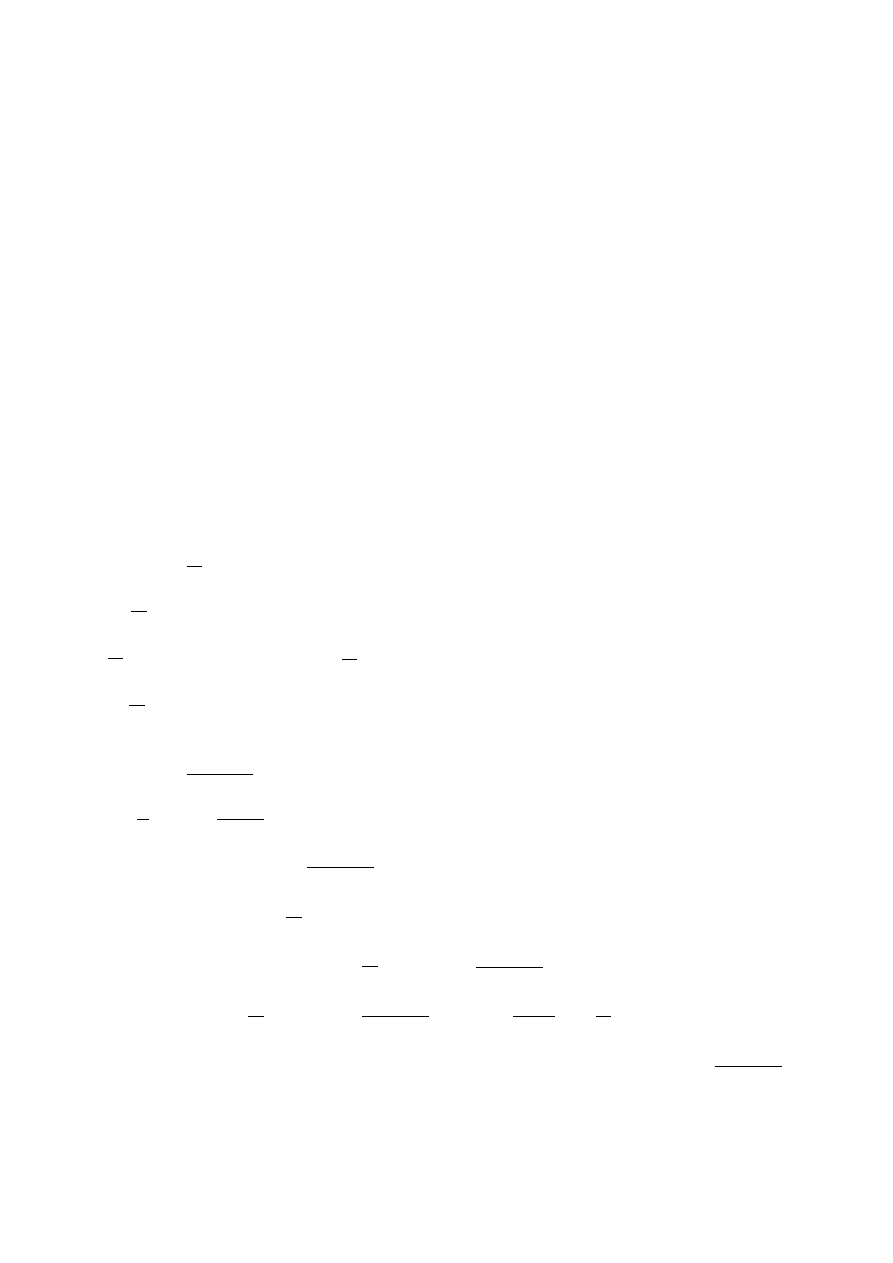
Dowód

Niech

S

n



n

∈ℕ

−ciąg sum cząstkowych szeregu

∑

n

=1

∞

−1

n

a

n

. Rozważmy dwa podciągi

ciągu S

n



n

∈ℕ

:

S

2 n



n

∈ℕ

i

S

2 n

−1



n

∈ℕ

.

Ponieważ

S

2 n

=−a

1

a

2

−a

3



≥0

a

4

−a

5



≥0

. . .a

2 n

−2

−a

2 n

−1



≥0

 a

0

2 n

zatem S

2 n

−a

1

.

Ponadto

S

2 n

2

−S

2 n

=a

2 n

2

−a

2 n

1

≤0 ⇒ S

2 n

2

≤S

2 n

⇒ S

2 n



n

∈ℕ

∈↘ .

Stąd wynika, że ciąg S

2 n



n

∈ℕ

jest zbieżny jako malejący i ograniczony od dołu, czyli

∃ lim

n

∞

S

2 n

=S . Nadto S

2 n

=S

2 n

−1

a

2 n

.

Zatem

lim

n

∞

S

2 n

−1

=lim

n

∞

S

2 n

−a

2 n

=S−0 =S .

Ponieważ dwa rozłączne podciągi S

2 n



n

∈ℕ

i S

2 n

−1



n

∈ℕ

wypełniają cały ciąg S

n



n

∈ℕ

i dążą do tej samej granicy, zatem

lim

n

∞

S

n

=S



Przykład

1)

∑

n

=1

∞

−1

n

1

n

−szereg anharmoniczny

a

n

=

1

n



1

n



n

∈ℕ

∈↘

lim

n

∞

1

n

=0

}

⇒

∑

n

=1

∞

−1

n

1

n

−zbieżny na podstawie kryterium Leibniza

2)

∑

n

=1

∞

−1

n

3

−−1

n

n

a

2 n

=

1
n

, a

2 n

−1

=

4

2 n

−1

⇒ a

2 n

a

2 n

−1

a

2 n

−2

⇒ a

n



n

∈ℕ

∉↘

Hipoteza: szereg

∑

n

=1

∞

−1

n

3

−−1

n

n

jest zbieżny.

Zauważmy, że

∑

n

=1

∞

−1

n

3

n

jest zbieżny na podstawie kryterium Leibniza.

Zatem różnica szeregów

∑

n

=1

∞

−1

n

3

n

i

∑

n

=1

∞

−1

n

3

−−1

n

n

jest szeregiem zbieżnym.

Jednakże

∑

n

=1

∞

−1

n

3

n

−

∑

n

=1

∞

−1

n

3

−−1

n

n

=

∑

n

=1

∞

−1

n

−1

n

n

=

∑

n

=1

∞

1

n

jest szeregiem

rozbieżnym, co daje sprzeczność. Stąd wynika rozbieżność szeregu

∑

n

=1

∞

−1

n

3

−−1

n

n

.

- 12 -

Uwaga

Jeśli szereg naprzemienny spełnia założenia kryterium Leibniza, to

∣

S

−S

n

∣

≤a

n

1

.

Uzasadnienie:

∣

S

−S

n

∣

=

∣

−1

n

1

a

n

1

−a

n

2

a

n

3

−. . .

∣

=

∣

a

n

1

−a

n

2

a

n

3

−. . .

∣

≤a

n

1

,

ponieważ ciąg jest malejący.

Łączność sumy szeregu zbieżnego

Pogrupujmy wyrazy szeregu

∑

n

=1

∞

a

n

, np. :

∑

n

=1

∞

a

n

=a

1

a

2

a

3



b

1

a

4

a

5



b

2

a

b

3

6

a

7

a

8

. . .

b

4

Twierdzenie

Jeśli

∑

n

=1

∞

a

n

−zbieżny ⇒

∑

n

=1

∞

b

n

− zbieżny ∧

∑

n

=1

∞

b

n

=

∑

n

=1

∞

a

n

.

Uwaga

Własności tej nie ma szereg rozbieżny.

Przykład

∑

n

=1

∞

−1

n

−szereg rozbieżny, jednak po przegrupowaniu wyrazów możemy otrzymać

Zmiana porządku wyrazów szeregu

Niech n

k



k

∈ℕ

- ciąg, w którym każda liczba naturalna występuje dokładnie raz.

Wtedy szeregi

∑

n

=1

∞

a

n

i

∑

k

=1

∞

a

n

k

różnią się tylko porządkiem wyrazów.

Twierdzenie

Jeżeli

∑

n

=1

∞

a

n

− zbieżny bezwzględnie ⇒

∑

k

=1

∞

a

n

k

−zbieżny bezwzględnie i

∑

k

=1

∞

a

n

k

=

∑

n

=1

∞

a

n

.

Uwaga

Własności tej nie ma szereg warunkowo zbieżny.

- 13 -

szereg zbieżny (lub rozbieżny), np.:

−11−11−11=000=0 (szereg zbieżny)

−11−11−1=−100=−1 (szereg zbieżny)

−11−11−11=

∑

n

=1

∞

−1

n

− rozbieżny

Przykład

∑

n

=1

∞

−1

n

1

1

n

− zbieżny warunkowo (bo

∑

n

=1

∞

1

n

− rozbieżny)

Niech S :

=

∑

n

=1

∞

−1

n

1

1
n

.

Zmieniamy porządek wyrazów szeregu:

∑

n

=1

∞

−1

n

1

1
n

=1 −

1
2



1
3

−

1
4



1
5

−

1
6



1
7

−

1
8



1
9

−

1

10



1

11

−

1

12

  =

?

=

?

1−

1
2



1
2

−

1
4



1
3

−

1
6



1
6

−

1
8



1
5

−

1

10



1

10

−

1

12

  =

1
2

−

1
4



1
6

−

1
8



1

10

−

1

12

  =

=

1
2

1 −

1
2



1
3

−

1
4



1
5

−  =

1
2

∑

n

=1

∞

−1

n

1

1
n

=

1
2

S

Zatem znak =

?

należy zastąpić znakiem

≠.

Twierdzenie Riemanna

W szeregu warunkowo zbieżnym można zmienić porządek wyrazów tak, by nowy szereg
był zbieżny do dowolnej wcześniej zadanej sumy, bądź tak, żeby był rozbieżny.

- 14 -