Ciągi funkcyjne

Niech X – zbiór,

Y , d  – przestrzeń metryczna.

oraz niech

∀ n∈ℕ f

n

: X

Y ,

czyli określony jest ciąg funkcyjny  f

n



n

∈ℕ

.

Niech f : X

Y.

Definicja

Mówimy, że ciąg funkcyjny  f

n



n

∈ℕ

zmierza punktowo

do funkcji f na zbiorze

X ,

jeśli dla każdego x

∈ X ciąg  f

n

 x

n

∈ℕ

zmierza do f

 x w przestrzeni Y

z metryką d, tzn.

f

n



X

f :

⇔ ∀ x∈ X lim

n

∞

d

 f

n

 x , f  x=0 ⇔

⇔ ∀ x∈ X ∀ 0 ∃n

0

∈ℕ ∀ nn

0

d

 f

n

 x , f  x

Funkcję f nazywamy

funkcją graniczną

.

Definicja

Ciąg  f

n



n

∈ℕ

zmierza jednostajnie

do f na zbiorze X , gdy:

Niech

X ,Y

– przestrzenie metryczne,

f

n

: X

Y ,

f : X

Y .

Definicja

Ciąg  f

n



n

∈ℕ

zmierza niemal jednostajnie

do funkcji f na zbiorze X, gdy:

f

n

f :

⇔ ∀ E ∈Comp X

f

n

f

Uwaga

- zbieżny jednostajnie

⇒  f

n



n

∈ℕ

- zbieżny niemal jednostajnie

⇒  f

n



n

∈ℕ

-

zbieżny punktowo.

- 1 -

f

f

n

:

⇔ ∀ 0 ∃n

0

∈ℕ ∀ nn

0

∀ x∈ X d  f

n

 x , f  x

X

Comp X

E

 f

n



n

∈ℕ

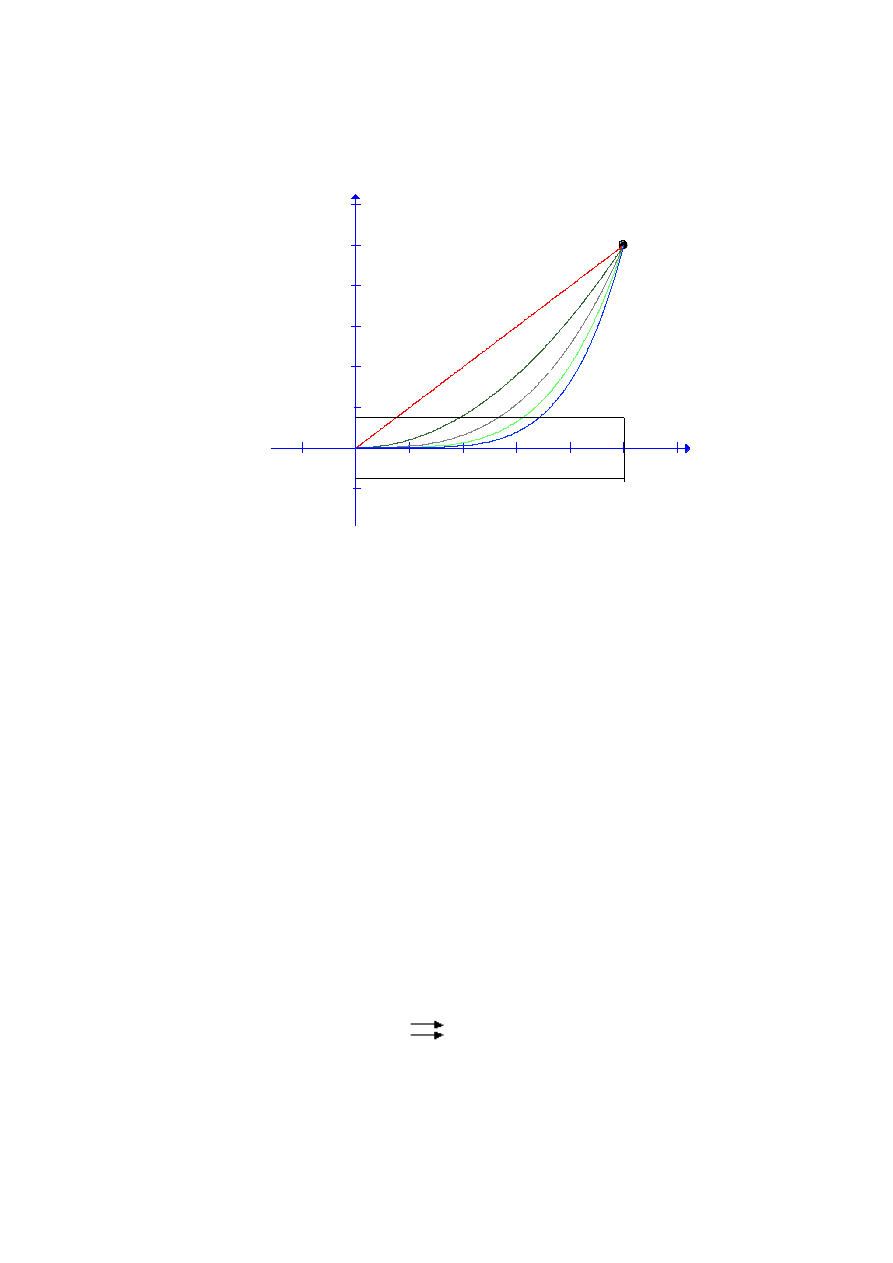
Przykład

Niech X

=[0;1]

oraz niech

f

n

 x=x

n

dla n

∈ℕ.

Ponieważ

lim

n

∞

x

n

=

{

więc ciąg  f

n



n

∈ℕ

jest zbieżny punktowo. Natomiast

nie jest zbieżny jednostajnie

, bo dla

wykres żadnej z funkcji f

n

nie znajduje się w całości w pasie

Zbadajmy teraz w X

=[ 0,1) zbieżność niemal jednostajną ciągu funkcyjnego  f

n



n

∈ℕ

.

Niech E

∈ Comp X . Stąd na podstawie twierdzenia charakteryzującego zbiory zwarte w

przestrzeni standardowej, zbiór E jest domknięty i ograniczony, tzn.

E

=[a ; b], gdzie 0≤a≤b1 .

Ponieważ 0≤d  x

n

,0

≤b

n

1 oraz

lim

n

∞

b

n

=0

zatem z twierdzenia o 3 ciągach wynika, że

a stąd wynika, że f

n

f .

Zatem  f

n



n

∈ℕ

jest zbieżny niemal jednostajnie w

X

=[ 0,1).

- 2 -

f(x)=x

f(x)=x^2

f(x)=x^3

f(x)=x^4

f(x)=x^5

f(x)=0.15

f(x)=-0.15

Series 1

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

1

1.2

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

1

1.2

x

y

f

1

f

2

f

3

f

4

f

5

−ε

ε

1

f

1

f

4

f

2

f

3

f

5

y

x

0 dla x

∈[ 0,1)

1 dla x

=1



−

−



x

∈[ 0,1)

[ 0,1)

×−,.

lim

n

∞

d

 x

n

, 0

=0,

E

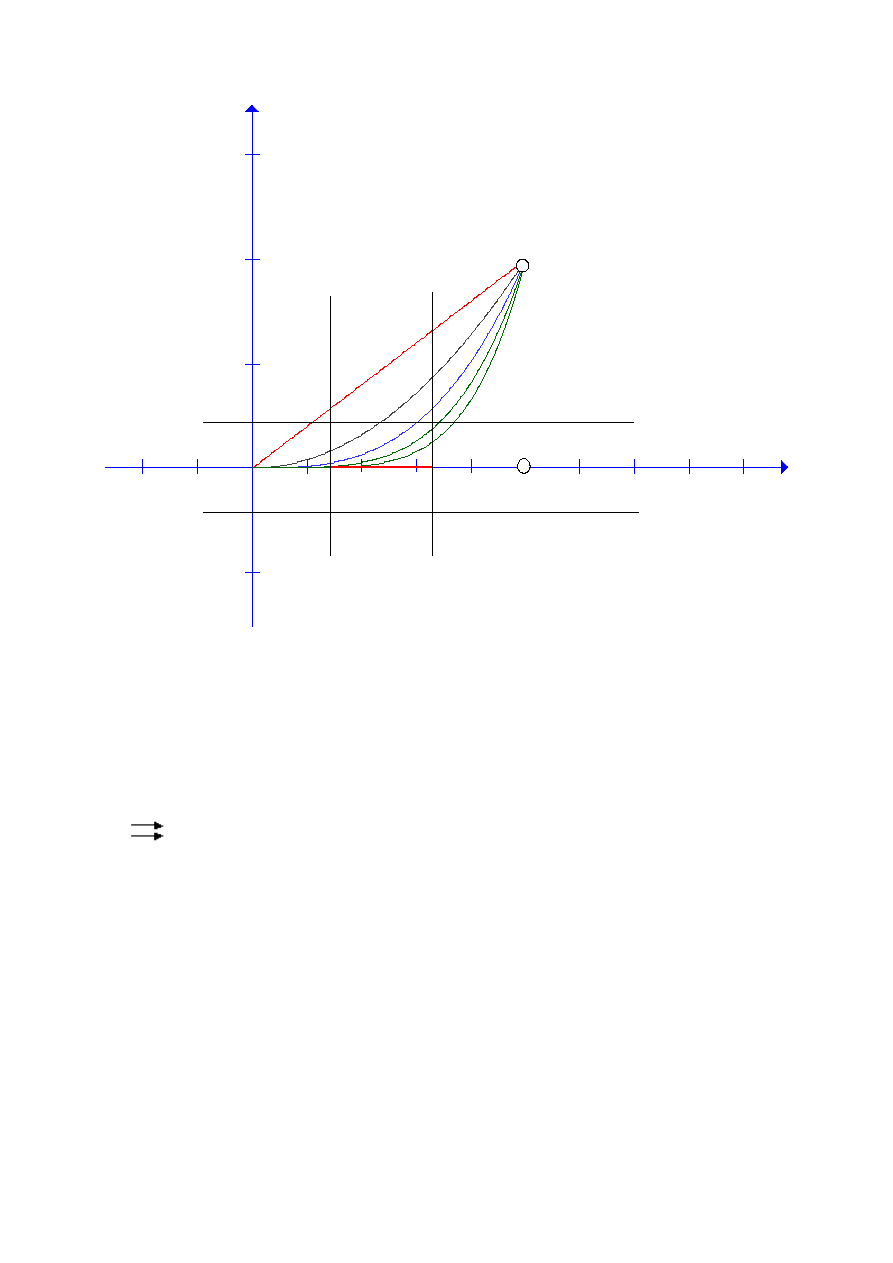
Twierdzenie

(o ciągłości funkcji granicznej)

}

⇒ f ∈C  X 

Wniosek

Jeśli funkcja graniczna ciągu funkcyjnego funkcji ciągłych nie jest ciągła, to ciąg nie jest
zbieżny jednostajnie.

- 3 -

∀ n∈ℕ f

n

∈C  X 

f

n

f

a

b

X

f(x)=x

f(x)=x^2

f(x)=x^3

f(x)=x^4

f(x)=x^5

Series 1

Series 2

-0.4

-0.2

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

-0.5

0.5

1

1.5

x

y

a

b

E

x

y



−

Przykład

c.d.

f

 x=

{

a wtedy

f

n

∈C  X 

i f ∉C  X 

zatem

Twierdzenie

Niech  f

n



n

∈ℕ

⊂B ( X ,Y ), gdzie B ( X ,Y )={ f | f : X Y , f −funkcja graniczna }.

Wtedy

f

n

f

⇔ lim

n

∞

d

sup

 f

n

, f

=0

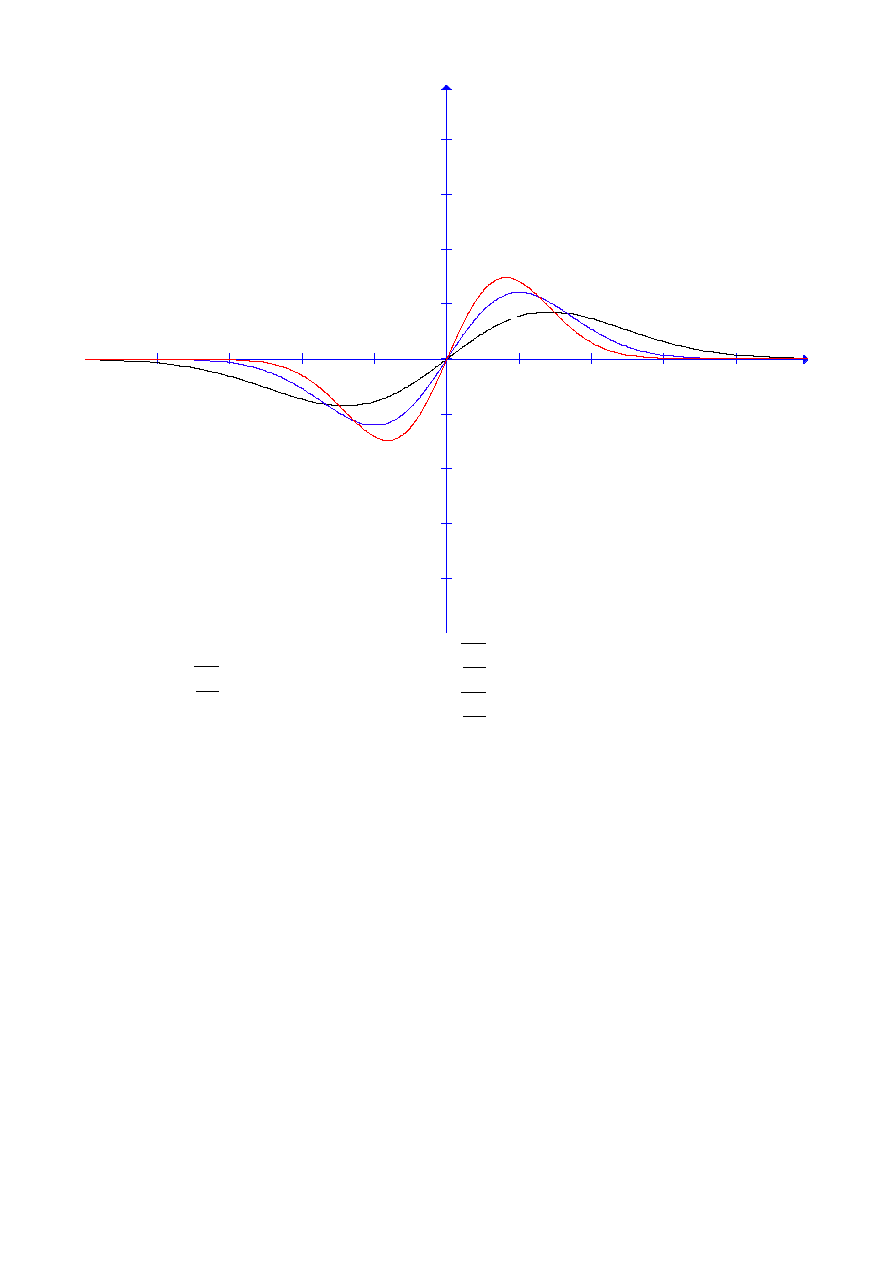
Przykład

Zbadać zbieżność jednostajną ciągu f

n

:

ℝ ℝ , gdzie f

n

 x=nxe

−nx

2

oraz określić obszary zbieżności punktowej D

p

i jednostajnej D

j

.

I. Aby zbadać zbieżność punktową, wybierzmy x

∈ℝ.

Wtedy

lim

n

∞

f

n

 x=lim

n

∞

nxe

−nx

2

=

{

bo dla x

≠0 mamy:

lim

n

∞

nx

e

nx

2

=

[

∞

∞

]

=

H

lim

n

 ∞

x

x

2

e

nx

2

=lim

n

∞

1

xe

nx

2

=0.

Zatem

∀ x∈ℝ lim

n

∞

f

n

 x=0 ⇒ f ≡0 ⇒ D

p

=ℝ.

II. Sprawdzamy, czy f

n

f .

f

n

∈C

f

n

−x=− f

n

 x, tzn. f jest funkcją nieparzystą

lim

x

 ∞

f

n

 x=lim

x

∞

nx
e

nx

2

=

H

lim

x

 ∞

n

2 nxe

nx

2

=0

}

⇒ f

n

∈Bℝ ,ℝ

Dla dowolnego

n∈ℕ mamy

d

sup

 f

n

, f

=sup

x

∈ℝ

∣ f

n

 x− f  x∣=sup

x

∈ℝ

∣ f

n

 x∣= sup

x

∈[0 ;∞ )

f

n

 x

- 4 -

0 dla x

∈

[

0;1



,

1 dla x

=1,

0 , gdy x

=0,

0 , gdy x

≠0,

X

X

Jeżeli f

n

 x=x

n

,

X

=[0;1], to

f .

f

n

X

Aby wyznaczyć kres górny wartości funkcji f

n

, zbadajmy jej ekstrema lokalne.

Ponieważ

f

n

'

 x=ne

−nx

2

−2 n

2

x

2

e

−nx

2

=n1−2 nx

2

e

−nx

2

=0

zatem

 f

n



max

= f

n





1

2 n



=



n

2 e

.

Stąd

sup

x

∈ℝ

∣ f

n

 x∣=max{ f

n



max

, lim

x

∞

f

n

 x}=max

{



n

2 e

, 0

}

=



n

2 e

,

więc

lim

n

∞

d

sup

 f

n

, f

=lim

n

∞



n

2 e

=∞≠0 ⇒

f

n

f

Wykażemy, że D

j

=(−∞ ; a ]∪[ b ;∞), gdzie a0b.

- 5 -

x

max

min

−



1

2 n



1

2 n

1

−2 nx

2

=0

x

=±



1

2 n

min

max

x

−



1

2 n



1

2 n

Ponieważ



1

2 n



n

∞

0

⇒

{

Niech n >max

{n

a

, n

b

} .

Wtedy

d

sup

 f

n

, f

=max{ f

n

b ,| f

n

a|, 0 }=max{nbe

−nb

2

,

−nae

−na

2

}.

Stąd

lim

n

∞

d

sup

 f

n

, f

=0.

Zatem

D

j

=(−∞ ; a ]∪[ b ;∞), gdzie a0b.

Twierdzenie

(o przejściu do granicy przy różniczkowaniu ciągu funkcyjnego)

}

⇒ lim

n

∞

f

n

'

 x=

[

lim

n

∞

f

n

 x

]

'

- 6 -

f

3

∃n

b

:

∀ nn

b



1

2 n

b

∃n

a

:

∀ nn

a

−



1

2 n

a

f

2

f

3

y

x

f(x)=x e^(-x^2)

f(x)=2x e^(-2x^2)

f(x)=3x e^(-3x^2)

-2

-1.5

-1

-0.5

0.5

1

1.5

2

-2

-1.5

-1

-0.5

0.5

1

1.5

2

x

y

f

1

f

2

f

3

f

1

x

y

Niech przedział I

⊂ℝ

f

n

: I

ℝ, n∈ℕ

f

n

∈D I  ∀ n∈ℕ

 f

n



n

∈ℕ

−zbieżny punktowo na I

 f

n

'



n

∈ℕ

−zbieżny jednostajnie na I

f

2

Twierdzenie

(o przejściu do granicy przy całkowaniu ciągu funkcyjnego)

}

⇒ ∀ x∈I lim

n

∞

∫

x

0

x

f

n

t dt=

∫

x

0

x



lim

n

∞

f

n

t 



dt

Przykład

c.d.

Jeśli

f

n

 x=nxe

−nx

2

,

to funkcja graniczna f

≡0 .

Niech x

0

=0 . Wtedy

∫

0

x



lim

n

∞

f

n

t 



dt

=

∫

0

x

0 dt

=0

∫

0

x

f

n

t dt=

∫

0

x

nte

−nt

2

dt

=−

1

2

e

−nt

2

0

x

=

1

2



1

−e

−nx

2





n

∞

1
2

}

- 7 -

⇒ f

n

f

Niech przedział I

⊂ℝ

f

n

: I

ℝ, n∈ℕ

x

0

∈I

f

n

−całkowalna ∀ n∈ℕ

 f

n



n

∈ℕ

−zbieżny jednostajnie