00 WST

00 WST

Ę

Ę

P

P

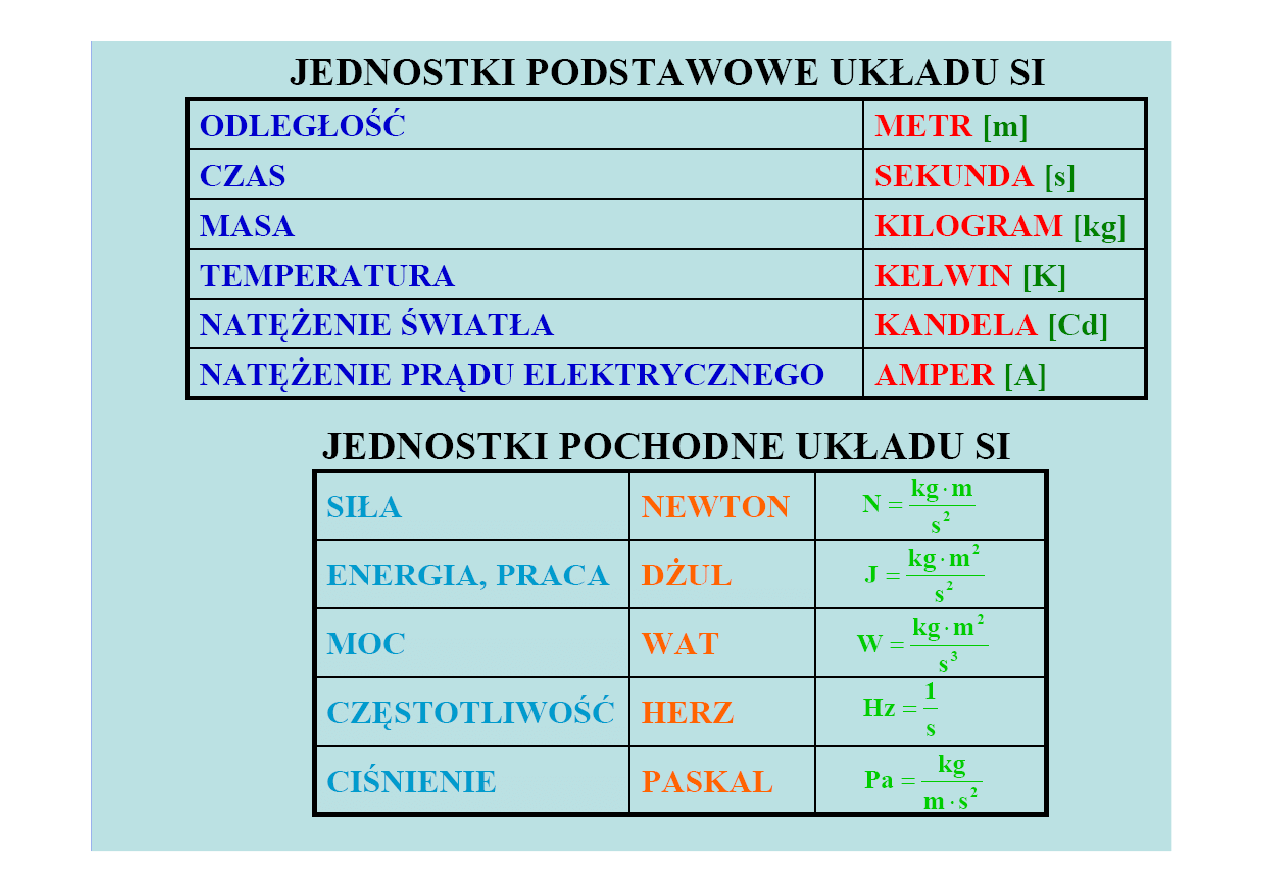
FIZYKA

(z gr.

Φύσις

Φύσις

physis - "natura")

nauka

nauka

o

o

przyrodzie

przyrodzie

w najszerszym znaczeniu tego słowa.

FIZYK

FIZYK

(z gr.

(z gr.

physikos

physikos

) = znawca przyrody

) = znawca przyrody

(w

(w

staro

staro

ż

ż

. tak

. tak

ż

ż

e lekarz)

e lekarz)

Fizycy badaj

ą

wła

ś

ciwo

ś

ci i przemiany

materii

materii

i

i

energii

energii

oraz

oraz

oddzia

oddzia

ł

ł

ywanie

ywanie

mi

mi

ę

ę

dzy

dzy

nimi.

nimi.

Do opisu zjawisk fizycznych u

ż

ywaj

ą

wielko

wielko

ś

ś

ci fizycznych

ci fizycznych

, wyra

ż

onych

za pomoc

ą

poj

ęć

matematycznych, takich jak liczba (skalar), wektor, tensor.

Tworz

ą

c hipotezy i teorie fizyka buduje relacje pomi

ę

dzy wielko

ś

ciami fizycznymi

reprezentowane przez równania matematyczne.

Fizyka jest

ś

ci

ś

le zwi

ą

zana z innymi naukami przyrodniczymi, szczególnie z

chemi

ą

jako

nauk

ą

o cz

ą

steczkach i zwi

ą

zkach chemicznych,

Fizyka zajmuje szczeg

Fizyka zajmuje szczeg

ó

ó

lne miejsce w naukach przyrodniczych,

lne miejsce w naukach przyrodniczych,

poniewa

poniewa

ż

ż

wyja

wyja

ś

ś

nia podstawowe zale

nia podstawowe zale

ż

ż

no

no

ś

ś

ci obowi

ci obowi

ą

ą

zuj

zuj

ą

ą

ce w przyrodzie.

ce w przyrodzie.

JAK BADAMY

JAK BADAMY

Ś

Ś

WIAT?

WIAT?

Odkrywanie nowych

Odkrywanie nowych

zjawisk i prawid

zjawisk i prawid

ł

ł

owo

owo

ś

ś

ci

ci

pomi

pomi

ę

ę

dzy nimi

dzy nimi

Sprawdzanie

Sprawdzanie

przewidywa

przewidywa

ń

ń

teoretycznych

teoretycznych

Przewidywanie

Przewidywanie

nowych zjawisk

nowych zjawisk

Wyja

Wyja

ś

ś

nianie obserwowanych

nianie obserwowanych

zjawisk zgodnie z

zjawisk zgodnie z

tworzonymi regu

tworzonymi regu

ł

ł

ami

ami

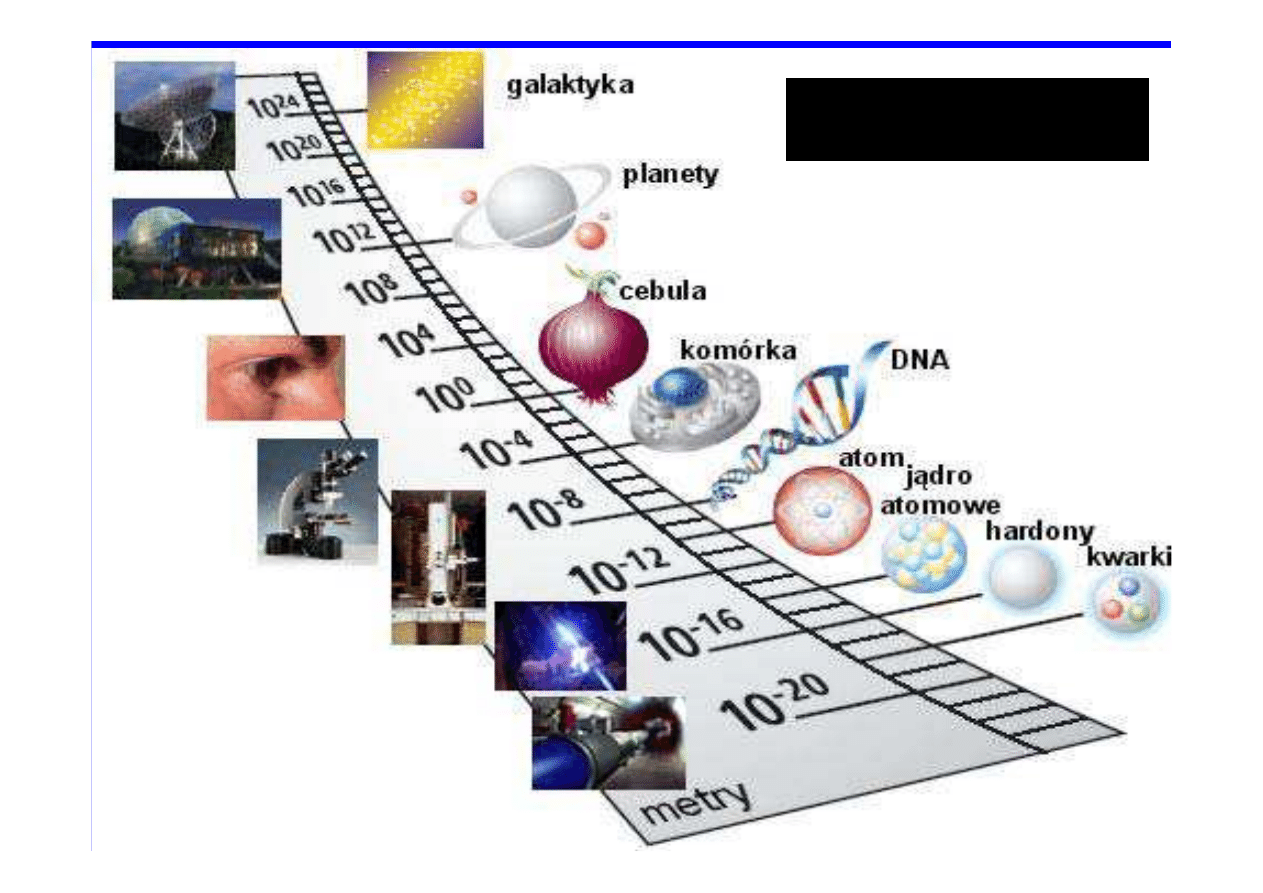
JAKIE OBIEKTY BADA

JAKIE OBIEKTY BADA

FIZYKA

FIZYKA

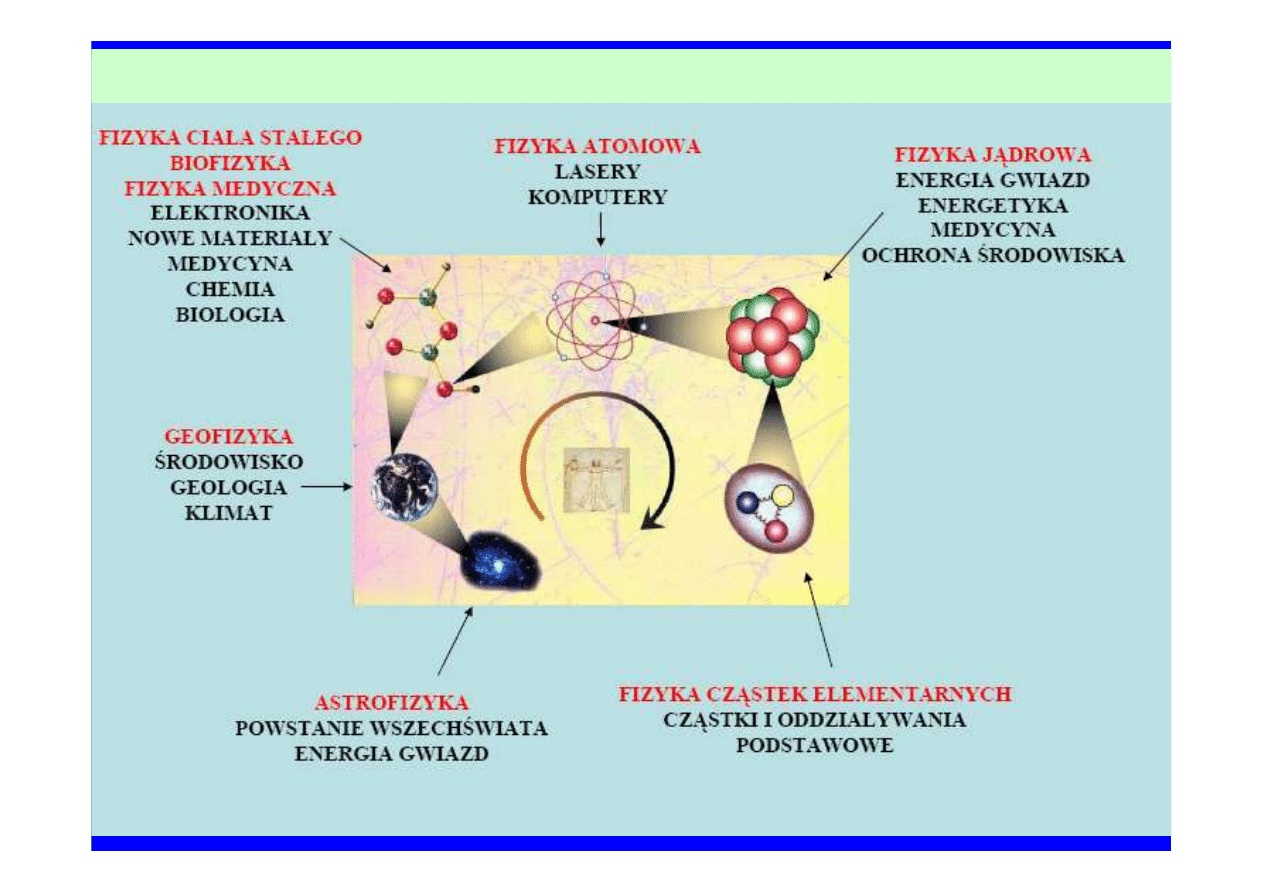
RÓ

ś

NE PRZYKŁADOWE DZIAŁY FIZYKI

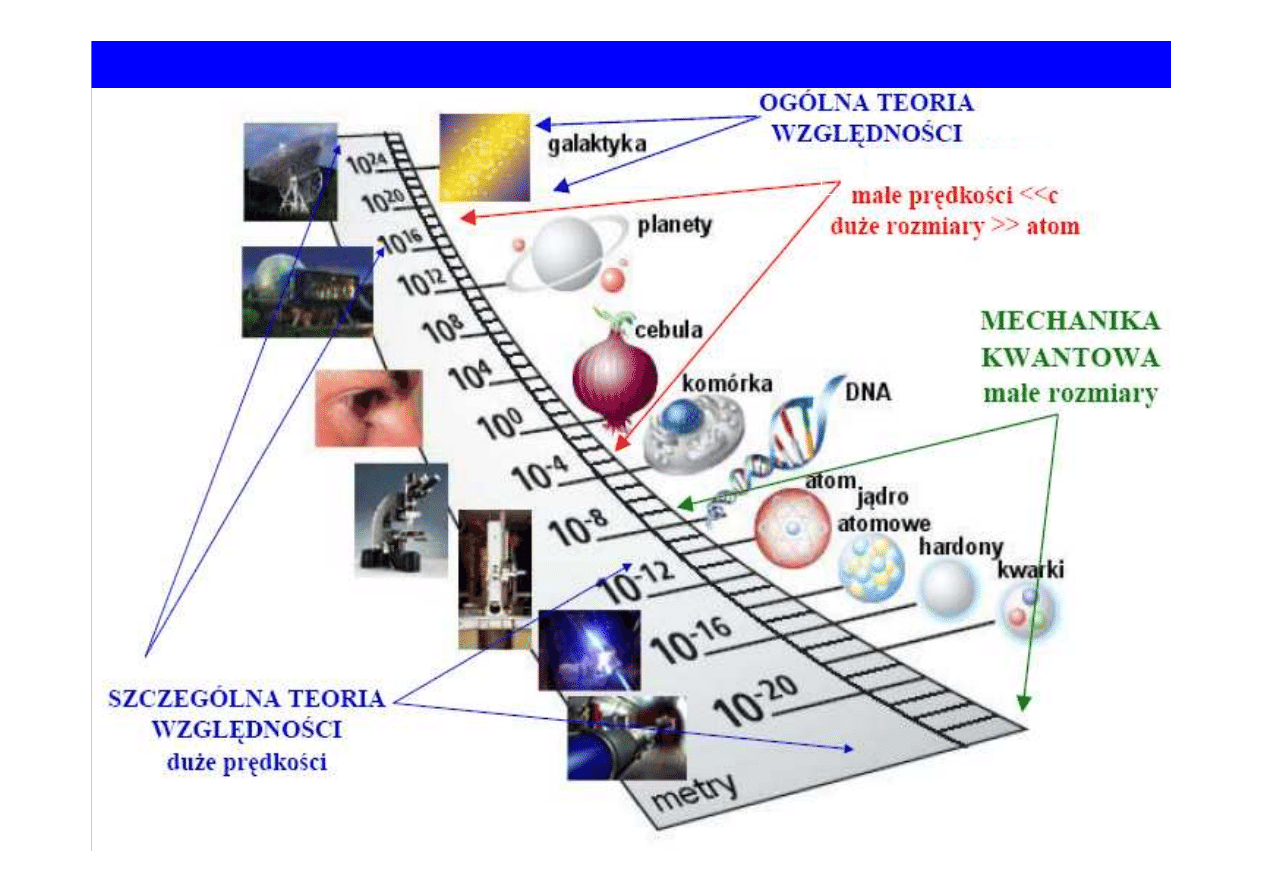
MECHANIKA KLASYCZNA

MECHANIKA

MECHANIKA

-

-

I JEJ R

I JEJ R

Ó

Ó

ś

ś

NE

NE

„

„

ODMIANY

ODMIANY

”

”

KINEMATYKA

KINEMATYKA

-

-

opis ruchu cia

opis ruchu cia

ł

ł

:

:

Wymaga on wybrania

Wymaga on wybrania

uk

uk

ł

ł

adu odniesienia

adu odniesienia

, wzgl

, wzgl

ę

ę

dem kt

dem kt

ó

ó

rego nasz ruch

rego nasz ruch

analizujemy.

analizujemy.

Jako uk

Jako uk

ł

ł

ad odniesienia mo

ad odniesienia mo

ż

ż

e by

e by

ć

ć

wybrany inny obiekt lub zbi

wybrany inny obiekt lub zbi

ó

ó

r obiekt

r obiekt

ó

ó

w.

w.

Z wybranym układem odniesienia mo

ż

emy zwi

ą

za

ć

uk

uk

ł

ł

ad wsp

ad wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych

dnych

.

Pozwala on ilo

Pozwala on ilo

ś

ś

ciowo

ciowo

-

-

przy pomocy liczb

przy pomocy liczb

–

–

okre

okre

ś

ś

la

la

ć

ć

po

po

ł

ł

o

o

ż

ż

enia

enia

i zmiany po

i zmiany po

ł

ł

o

o

ż

ż

e

e

ń

ń

czyli ruch.

czyli ruch.

Z uk

Z uk

ł

ł

adem odniesienia mo

adem odniesienia mo

ż

ż

na zwi

na zwi

ą

ą

za

za

ć

ć

wiele ( w zasadzie niesko

wiele ( w zasadzie niesko

ń

ń

czenie

czenie

wiele) rodzaj

wiele) rodzaj

ó

ó

w wsp

w wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych.

dnych.

O

O

O

O

RÓ

ś

NE SPOSOBY WPROWADZANIA WSPÓŁRZ

Ę

DNYCH W WYBRANYM

UKŁADZIE ODNIESIENIA

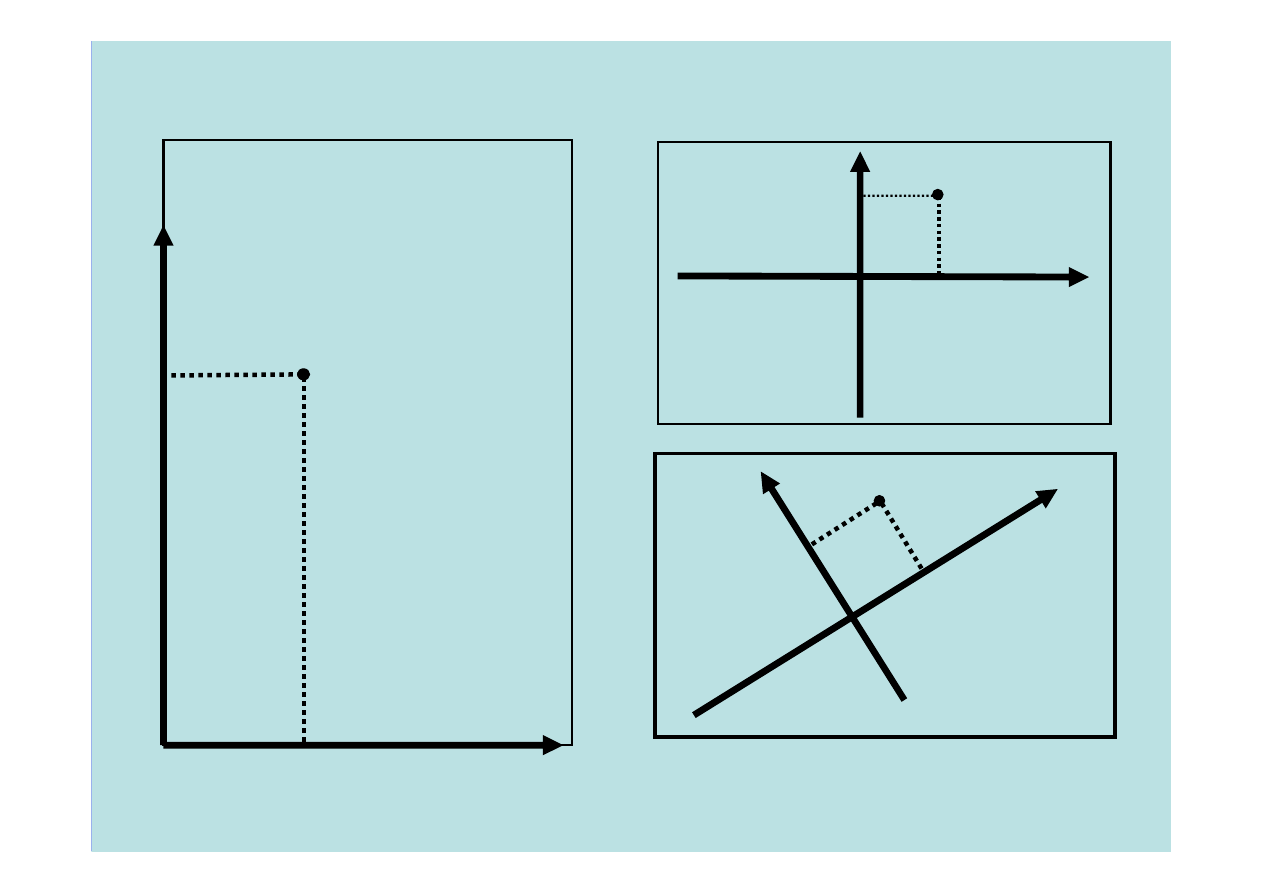
Przyk

Przyk

ł

ł

ad:

ad:

rozwa

rozwa

ż

ż

my kartk

my kartk

ę

ę

w kratk

w kratk

ę

ę

z zeszytu, po kt

z zeszytu, po kt

ó

ó

rej chodzi mr

rej chodzi mr

ó

ó

wka.

wka.

Brzegi kartki mog

Brzegi kartki mog

ą

ą

by

by

ć

ć

uk

uk

ł

ł

adem odniesienia

adem odniesienia

dla analizy ruchu mr

dla analizy ruchu mr

ó

ó

wki.

wki.

Rol

Rol

ę

ę

uk

uk

ł

ł

adu wsp

adu wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych

dnych

mog

mog

ą

ą

pe

pe

ł

ł

ni

ni

ć

ć

linie tworz

linie tworz

ą

ą

ce siatk

ce siatk

ę

ę

kratek.

kratek.

Jako

Jako

pocz

pocz

ą

ą

tek uk

tek uk

ł

ł

adu wsp

adu wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych

dnych

mo

mo

ż

ż

na wybra

na wybra

ć

ć

dowolny punkt na

dowolny punkt na

kartce

kartce

–

–

np

np

. mo

. mo

ż

ż

e to by

e to by

ć

ć

jeden z naro

jeden z naro

ż

ż

nik

nik

ó

ó

w kartki lub punkt na

w kartki lub punkt na

ś

ś

rodku.

rodku.

Mo

Mo

ż

ż

esz na wiele sposob

esz na wiele sposob

ó

ó

w wybra

w wybra

ć

ć

osie wsp

osie wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych oraz numeracj

dnych oraz numeracj

ę

ę

kratek czyli

kratek czyli

mo

mo

ż

ż

esz zdefiniowa

esz zdefiniowa

ć

ć

na wiele sposob

na wiele sposob

ó

ó

w uk

w uk

ł

ł

ady

ady

wsp

wsp

ó

ó

ł

ł

rz

rz

ę

ę

d

d

-

-

nych na swojej kartce

nych na swojej kartce

. Uk

. Uk

ł

ł

ad wsp

ad wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych wprowadzamy zwykle w

dnych wprowadzamy zwykle w

taki spos

taki spos

ó

ó

b aby opis analizowanego ruchu by

b aby opis analizowanego ruchu by

ł

ł

jak najbardziej wygodny.

jak najbardziej wygodny.

Innym przyk

Innym przyk

ł

ł

adem

adem

uk

uk

ł

ł

adu wsp

adu wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych

dnych

jest znany wszystkim uk

jest znany wszystkim uk

ł

ł

ad

ad

wsp

wsp

ó

ó

ł

ł

rz

rz

ę

ę

dnych geograficznych

dnych geograficznych

na powierzchni Ziemi. Tu tak

na powierzchni Ziemi. Tu tak

ż

ż

e istnia

e istnia

ł

ł

o

o

wiele mo

wiele mo

ż

ż

liwo

liwo

ś

ś

ci wprowadzenia punktu pocz

ci wprowadzenia punktu pocz

ą

ą

tkowego oraz linii

tkowego oraz linii

pocz

pocz

ą

ą

tkowych. Np.

tkowych. Np.

ż

ż

adne prawo przyrody nie nakazuje aby po

adne prawo przyrody nie nakazuje aby po

ł

ł

udnik

udnik

zerowy, od kt

zerowy, od kt

ó

ó

rego odliczamy d

rego odliczamy d

ł

ł

ugo

ugo

ść

ść

geograficzn

geograficzn

ą

ą

przechodzi

przechodzi

ł

ł

akurat

akurat

przez Londyn. O takim wyborze zadecydowa

przez Londyn. O takim wyborze zadecydowa

ł

ł

y r

y r

ó

ó

ż

ż

ne wzgl

ne wzgl

ę

ę

dy praktyczne

dy praktyczne

i historyczne.

i historyczne.

αααα

r

x

x

y

}}}}

y

x

αααα

⋅⋅⋅⋅

====

αααα

⋅⋅⋅⋅

====

sin

r

y

cos

r

x

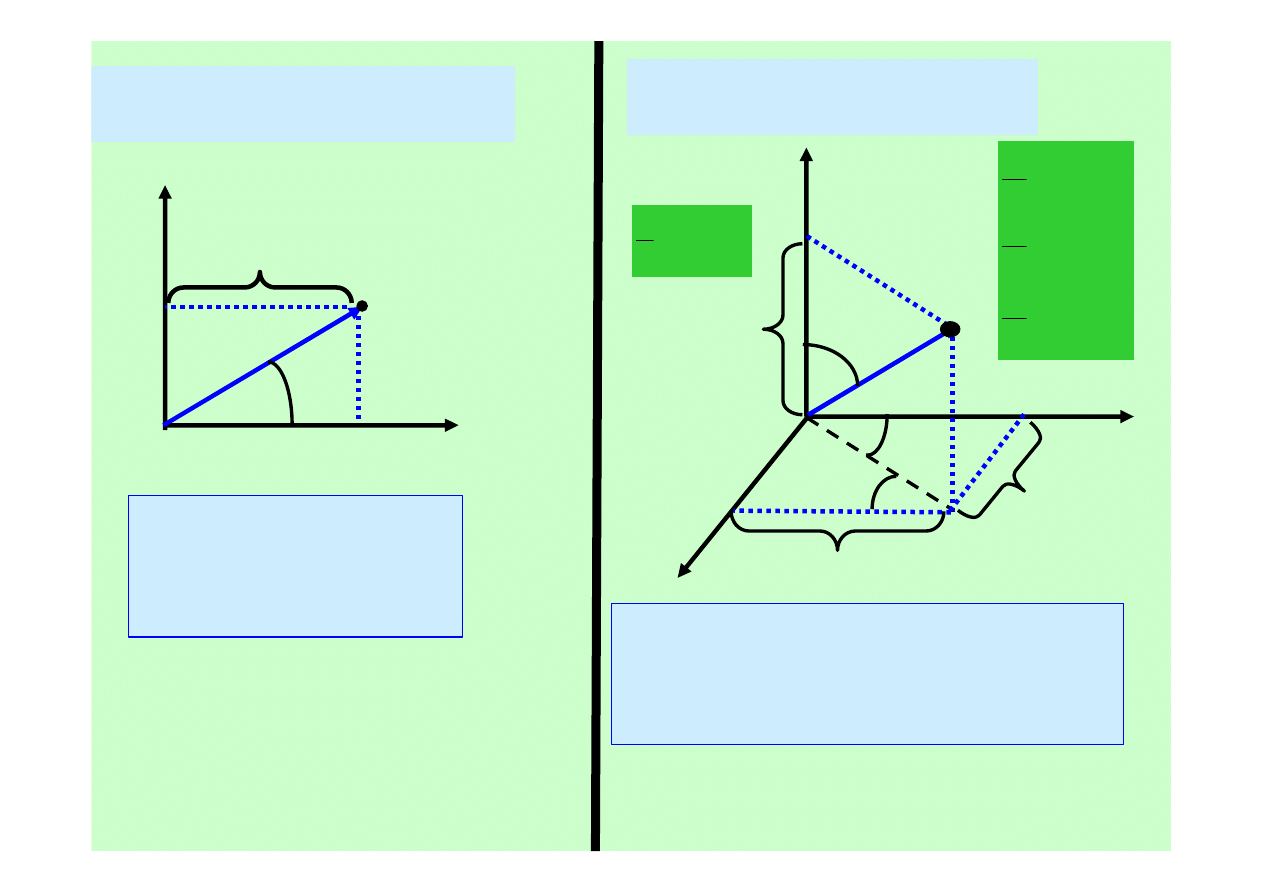
WSP

WSP

Ó

Ó

Ł

Ł

RZ

RZ

Ę

Ę

DNE BIEGUNOWE

DNE BIEGUNOWE

NA P

NA P

Ł

Ł

ASZCZY

ASZCZY

Ź

Ź

NIE

NIE

WSP

WSP

Ó

Ó

Ł

Ł

RZ

RZ

Ę

Ę

DNE SFERYCZNE

DNE SFERYCZNE

W PRZESTRZENI

W PRZESTRZENI

3D

3D

X

y

z

r

P

P

y

x

x

αααα

ββββ

ββββ

r’

P’

r’

ββββ

====

ββββ

====

αααα

====

cos

'

r

y

sin

'

r

x

sin

r

'

r

αααα

====

cos

r

z

αααα

⋅⋅⋅⋅

====

ββββ

⋅⋅⋅⋅

αααα

⋅⋅⋅⋅

====

ββββ

⋅⋅⋅⋅

====

ββββ

⋅⋅⋅⋅

αααα

⋅⋅⋅⋅

====

ββββ

⋅⋅⋅⋅

====

cos

r

z

cos

sin

r

cos

'

r

y

sin

sin

r

sin

'

r

x

PRZYPOMNIENIE PODSTAWOWYCH WIADOMO

PRZYPOMNIENIE PODSTAWOWYCH WIADOMO

Ś

Ś

CI Z KINEMATYKI

CI Z KINEMATYKI

PUNKTU MATERIALNEGO

PUNKTU MATERIALNEGO

Ze wzgl

Ze wzgl

ę

ę

du na kszta

du na kszta

ł

ł

t toru mo

t toru mo

ż

ż

emy podzieli

emy podzieli

ć

ć

ruchy na:

ruchy na:

prostoliniowe,

krzywoliniowe - otwarte lub zamkni

ę

te.

Ze wzgl

Ze wzgl

ę

ę

du na zachowanie si

du na zachowanie si

ę

ę

pr

pr

ę

ę

dko

dko

ś

ś

ci w czasie ruchu mamy mo

ci w czasie ruchu mamy mo

ż

ż

liwy

liwy

podzia

podzia

ł

ł

na:

na:

ruch jednostajny

ruch jednostajny

, w kt

, w kt

ó

ó

rym sta

rym sta

ł

ł

a w czasie pozostaje warto

a w czasie pozostaje warto

ść

ść

wektora pr

wektora pr

ę

ę

dko

dko

ś

ś

ci (czyli szybko

ci (czyli szybko

ść

ść

cia

cia

ł

ł

a)

a)

ruch niejednostajny

ruch niejednostajny

, w kt

, w kt

ó

ó

rym szybko

rym szybko

ść

ść

cia

cia

ł

ł

a zmienia si

a zmienia si

ę

ę

w czasie.

w czasie.

Bior

Bior

ą

ą

c pod uwag

c pod uwag

ę

ę

zar

zar

ó

ó

wno kszta

wno kszta

ł

ł

t toru jak i zachowanie si

t toru jak i zachowanie si

ę

ę

wektora

wektora

pr

pr

ę

ę

dko

dko

ś

ś

ci mamy nast

ci mamy nast

ę

ę

puj

puj

ą

ą

ce mo

ce mo

ż

ż

liwo

liwo

ś

ś

ci:

ci:

ruch jednostajny prostoliniowy

ruch jednostajny prostoliniowy

–

–

w kt

w kt

ó

ó

rym wektor pr

rym wektor pr

ę

ę

dko

dko

ś

ś

ci nie zmienia

ci nie zmienia

w czasie ruchu swojej warto

w czasie ruchu swojej warto

ś

ś

ci (sta

ci (sta

ł

ł

a szybko

a szybko

ść

ść

) ani kierunku i zwrotu;

) ani kierunku i zwrotu;

ruch niejednostajny prostoliniowy

ruch niejednostajny prostoliniowy

–

–

tu wektor pr

tu wektor pr

ę

ę

dko

dko

ś

ś

ci nie zmienia

ci nie zmienia

kierunku lecz zmienia si

kierunku lecz zmienia si

ę

ę

jego warto

jego warto

ść

ść

(zmienna szybko

(zmienna szybko

ść

ść

);

);

ruch jednostajny krzywoliniowy

ruch jednostajny krzywoliniowy

–

–

tu sta

tu sta

ł

ł

a jest szybko

a jest szybko

ść

ść

(czyli warto

(czyli warto

ść

ść

wektora pr

wektora pr

ę

ę

dko

dko

ś

ś

ci) lecz zmienny w czasie jest kierunek

ci) lecz zmienny w czasie jest kierunek

wektora pr

wektora pr

ę

ę

dko

dko

ś

ś

ci;

ci;

ruch niejednostajny krzywoliniowy

ruch niejednostajny krzywoliniowy

–

–

czyli ruch, w kt

czyli ruch, w kt

ó

ó

rym zmienna w czasie

rym zmienna w czasie

jest zar

jest zar

ó

ó

wno szybko

wno szybko

ść

ść

jak i kierunek wektora pr

jak i kierunek wektora pr

ę

ę

dko

dko

ś

ś

ci.

ci.

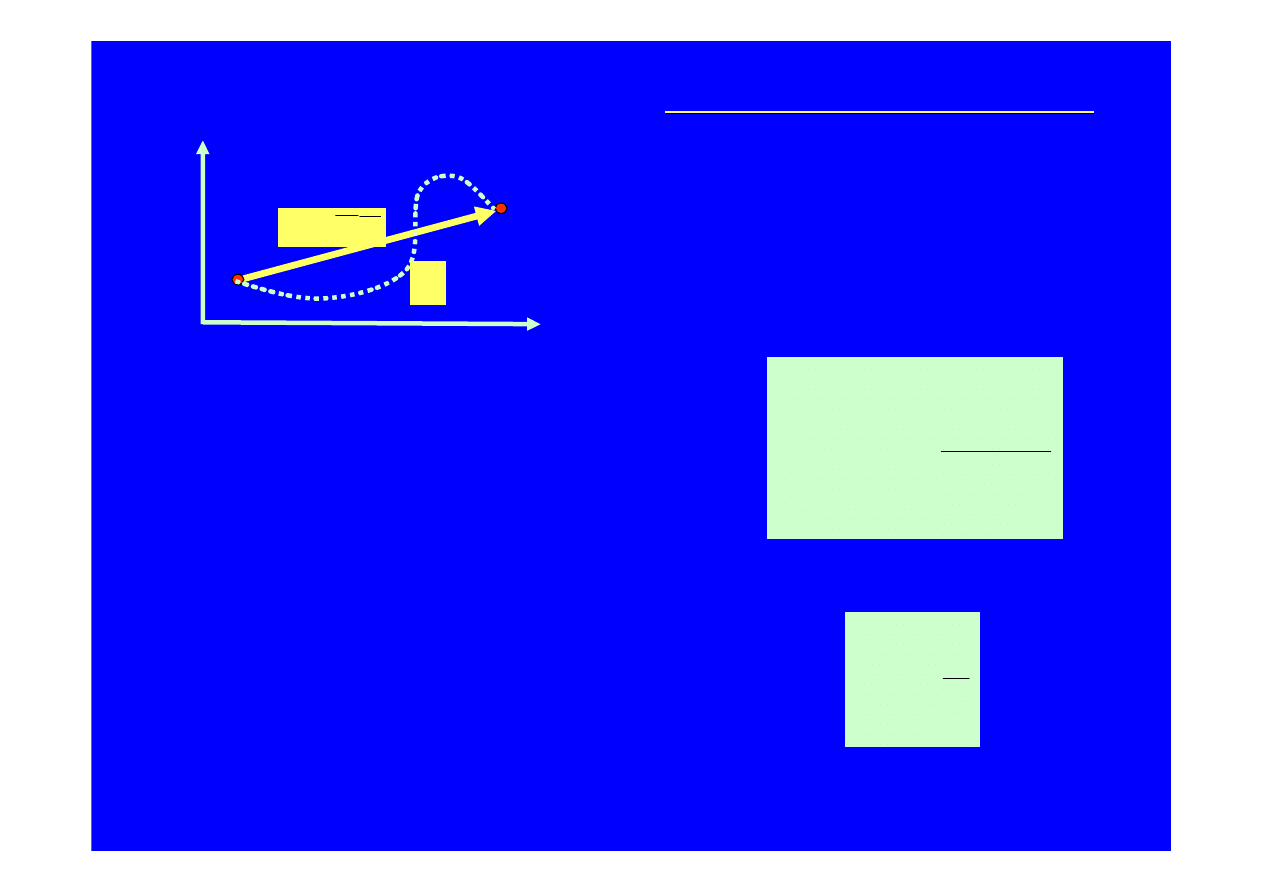
Zmian

Zmian

ę

ę

po

po

ł

ł

o

o

ż

ż

enia punktu w ruchu ilustruje

enia punktu w ruchu ilustruje

WEKTOR PRZEMIESZCZENIA

WEKTOR PRZEMIESZCZENIA

A

A

B

B

B

A

L

====

r

s

s

s

Warto

Warto

ść

ść

wektora przemieszczenia

wektora przemieszczenia

AB

AB

na og

na og

ó

ó

ł

ł

nie musi by

nie musi by

ć

ć

to

to

ż

ż

sama z przebyt

sama z przebyt

ą

ą

drog

drog

ą

ą

s

s

Wektor pr

Wektor pr

ę

ę

dko

dko

ś

ś

ci

ci

ś

ś

redniej na odcinku AB :

redniej na odcinku AB :

t

B

A

V

ś

r

∆∆∆∆

====

r

r

Czym

Czym

ś

ś

innym na og

innym na og

ó

ó

ł

ł

mo

mo

ż

ż

e by

e by

ć

ć

ś

ś

rednia warto

rednia warto

ść

ść

pr

pr

ę

ę

dko

dko

ś

ś

ci rozumiana jako

ci rozumiana jako

iloraz przebytej drogi,

iloraz przebytej drogi,

s

s

, przez czas ruchu,

, przez czas ruchu,

t

t

, czyli:

, czyli:

przy czym nie musi to by

przy czym nie musi to by

ć

ć

ruch jednostajny.

ruch jednostajny.

t

s

v

====

Oczywi

Oczywi

ś

ś

cie w ruchu jednostajnym warto

cie w ruchu jednostajnym warto

ść

ść

pr

pr

ę

ę

dko

dko

ś

ś

ci

ci

w ka

w ka

ż

ż

dej chwili jest to

dej chwili jest to

ż

ż

sama z jej warto

sama z jej warto

ś

ś

ci

ci

ą

ą

ś

ś

redni

redni

ą

ą

.

.

x

y

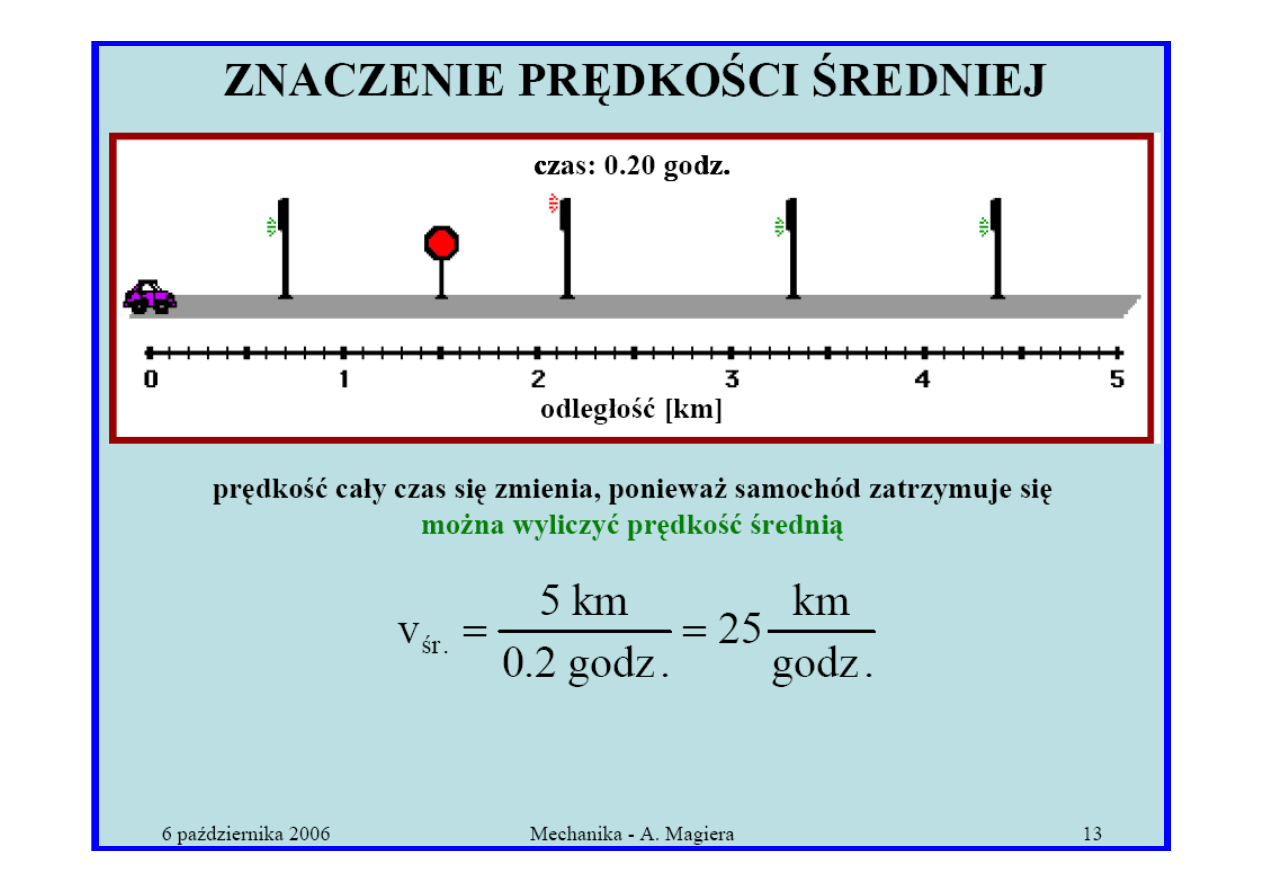
D Y N A M I K A

D Y N A M I K A

Jest nauk

Jest nauk

ą

ą

o si

o si

ł

ł

ach i ich zwi

ach i ich zwi

ą

ą

zku z ruchem

zku z ruchem

Si

Si

ł

ł

a jest wielko

a jest wielko

ś

ś

ci

ci

ą

ą

WEKTOROW

WEKTOROW

Ą

Ą

.

.

Jednostk

Jednostk

ą

ą

si

si

ł

ł

y jest

y jest

1 niuton [1 N] .

1 niuton [1 N] .

1 niuton to si

1 niuton to si

ł

ł

a, kt

a, kt

ó

ó

ra masie 1 kg

ra masie 1 kg

nadaje przyspieszenie 1 m/

nadaje przyspieszenie 1 m/

s

s

2

2

2

s

m

1

kg

1

N

1

⋅⋅⋅⋅

====

I

I

-

-

sza ZASADA DYNAMIKI NEWTONA

sza ZASADA DYNAMIKI NEWTONA

Je

Je

ś

ś

li na cia

li na cia

ł

ł

o nie dzia

o nie dzia

ł

ł

a

a

ż

ż

adna si

adna si

ł

ł

a lub dzia

a lub dzia

ł

ł

aj

aj

ą

ą

ce si

ce si

ł

ł

y r

y r

ó

ó

wnowa

wnowa

żą

żą

si

si

ę

ę

to cia

to cia

ł

ł

o

o

nie zmienia stanu swojego ruchu (czyli pozostaje w spoczynku lub

nie zmienia stanu swojego ruchu (czyli pozostaje w spoczynku lub

w ruchu

w ruchu

jednostajnym prostoliniowym).

jednostajnym prostoliniowym).

Uk

Uk

ł

ł

ady odniesienia, w kt

ady odniesienia, w kt

ó

ó

rych spe

rych spe

ł

ł

niona jest powy

niona jest powy

ż

ż

sza zasada (nazywana tak

sza zasada (nazywana tak

ż

ż

e

e

zasad

zasad

ą

ą

bezw

bezw

ł

ł

adno

adno

ś

ś

ci) nosz

ci) nosz

ą

ą

nazw

nazw

ę

ę

uk

uk

ł

ł

ad

ad

ó

ó

w inercjalnych.

w inercjalnych.

Najwi

Najwi

ę

ę

ksza warto

ksza warto

ść

ść

I zasady dynamiki Newtona tkwi w tym,

I zasady dynamiki Newtona tkwi w tym,

ż

ż

e postuluje ona

e postuluje ona

istnienie inercjalnych uk

istnienie inercjalnych uk

ł

ł

ad

ad

ó

ó

w odniesienia.

w odniesienia.

M

M

ó

ó

wi,

wi,

ż

ż

e aby zmieni

e aby zmieni

ć

ć

ruch cia

ruch cia

ł

ł

a potrzebne jest dzia

a potrzebne jest dzia

ł

ł

anie si

anie si

ł

ł

y.

y.

W szczeg

W szczeg

ó

ó

lno

lno

ś

ś

ci

ci

, gdy na cia

gdy na cia

ł

ł

o dzia

o dzia

ł

ł

a sta

a sta

ł

ł

a niezr

a niezr

ó

ó

wnowa

wnowa

ż

ż

ona si

ona si

ł

ł

a to cia

a to cia

ł

ł

o

o

porusza si

porusza si

ę

ę

ruchem jednostajnie przyspieszonym z przyspieszeniem wprost

ruchem jednostajnie przyspieszonym z przyspieszeniem wprost

proporcjonalnym do dzia

proporcjonalnym do dzia

ł

ł

aj

aj

ą

ą

cej si

cej si

ł

ł

y i odwrotnie proporcjonalnym do jego masy

y i odwrotnie proporcjonalnym do jego masy

,

co zapisujemy:

co zapisujemy:

.

Si

Si

ł

ł

a i przyspieszenie s

a i przyspieszenie s

ą

ą

wektorami maj

wektorami maj

ą

ą

cymi ten sam kierunek i zwrot.

cymi ten sam kierunek i zwrot.

II ZASADA DYNAMIKI NEWTONA

II ZASADA DYNAMIKI NEWTONA

m

F

a

r

r

====

t

p

t

v

m

a

m

F

∆∆∆∆

∆∆∆∆

====

∆∆∆∆

∆∆∆∆

====

====

r

r

r

r

Ka

Ka

ż

ż

da niezr

da niezr

ó

ó

wnowa

wnowa

ż

ż

ona si

ona si

ł

ł

a dzia

a dzia

ł

ł

aj

aj

ą

ą

ca na cia

ca na cia

ł

ł

o powoduje zmian

o powoduje zmian

ę

ę

jego p

jego p

ę

ę

du.

du.

gdzie wektor p

gdzie wektor p

ę

ę

du definiujemy :

du definiujemy :

v

m

p

r

r

⋅⋅⋅⋅

====

III ZASADA DYNAMIKI NEWTONA

III ZASADA DYNAMIKI NEWTONA

Odzia

Odzia

ł

ł

ywanie mi

ywanie mi

ę

ę

dzy obiektami jest zawsze

dzy obiektami jest zawsze

wzajemne

wzajemne

.

.

Jest to istotna tre

Jest to istotna tre

ść

ść

III zasady dynamiki:

III zasady dynamiki:

Je

Je

ś

ś

li cia

li cia

ł

ł

o

o

A

A

dzia

dzia

ł

ł

a na cia

a na cia

ł

ł

o

o

B

B

si

si

ł

ą

ł

ą

F

F

AB

AB

to cia

to cia

ł

ł

o

o

B

B

dzia

dzia

ł

ł

a na cia

a na cia

ł

ł

o

o

A

A

si

si

ł

ą

ł

ą

F

F

BA

BA

,

,

przy

przy

ł

ł

o

o

ż

ż

on

on

ą

ą

do cia

do cia

ł

ł

a

a

A

A

, maj

, maj

ą

ą

c

c

ą

ą

t

t

ą

ą

sam

sam

ą

ą

warto

warto

ść

ść

i kierunek lecz przeciwny zwrot;

i kierunek lecz przeciwny zwrot;

czyli :

czyli :

F

F

AB

AB

=

=

-

-

F

F

BA

BA

.

.

Uwaga!

Uwaga!

Si

Si

ł

ł

y wzajemnego oddzia

y wzajemnego oddzia

ł

ł

ywania (zwane cz

ywania (zwane cz

ę

ę

sto

sto

si

si

ł

ł

ami akcji i reakcji

ami akcji i reakcji

)

)

nie r

nie r

ó

ó

wnowa

wnowa

żą

żą

si

si

ę

ę

gdy

gdy

ż

ż

jedna dzia

jedna dzia

ł

ł

a na cia

a na cia

ł

ł

o A druga za

o A druga za

ś

ś

na cia

na cia

ł

ł

o B.

o B.

R

R

ó

ó

ż

ż

ne s

ne s

ą

ą

wi

wi

ę

ę

c punkty przy

c punkty przy

ł

ł

o

o

ż

ż

enia tych si

enia tych si

ł

ł

: jedna do cia

: jedna do cia

ł

ł

a A druga do cia

a A druga do cia

ł

ł

a B.

a B.

J. Sikorski, IFD

J. Sikorski, IFD

Uniwersytet Gda

Uniwersytet Gda

ń

ń

ski

ski