
1
Podstawy elektrotechniki
2
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
0
=
−
−
−
u
dt
di
L
Ri
U
z
dt
du
C
i=
R
L
U
z
t=
0
i
0
=
−
−
−
u
u
u
U
L
R
z
C
u
()
0
0
=
u
0
=
−
−
−
u
dt
du
C
dt
d
L
dt
du
RC
U
z
z
U
u
dt
du
RC
dt
u
d
LC
=
+
+
2
2
()
0
0
=
i
(
)
+
=
+
=
0
0
t
dt
du
C
i
()
C
i
dt
du
t
0
0
=
+
=
0
=
3
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
R
L
U
z
t=
0
i
C
u
()
0
0
=
u
z
U
u
dt
du
T
dt
u
d
T
=
+
+
δ
2
2
2
()
0
0
=
′
u
wprowa
dz
am
y zm
ie
nne
be
zw
ym
ia
rowe
:
T
t
=
τ
LC
T
=
RC
T
=
δ
z
U
u
=
ϑ
τ
ϑ
d
d
T
U
dt
du
z
=
2
2
2
2
2
τ
ϑ
d
d
T
U
dt
u
d
z
=
4
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
z
z
z
z
U
U
d
d
T
U
T
d
d
T
U
T
=
+
+
ϑ
τ
ϑ
τ
ϑ
δ
2
2
2
2
1
2
2
=
+
+
ϑ
τ
ϑ
τ
ϑ
δ
d
d
T
T
d
d
()
()
()
τ
ϑ
τ
ϑ
τ
ϑ
w
p
+
=
(
)
1
=
τ
ϑ
w
be
zw
ym
ia
rowe
wa
runk
i poc
zą
tkowe
:
()
()
0
0
0
=
=
z
U
u
ϑ
()
()
0
0
0
=
′
=
′
u
U
T
z
ϑ
τ
ϑ
d
d
T
U
dt
du
z
=
dt
du
U
T
d
d
z
=
τ
ϑ
0
0
=
=
=
t
z
dt
du
U
T
d
d
τ
τ
ϑ

2
5
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
()
τ
α
τ
α
τ
ϑ
2
1
2
1
e
A
e
A
p
+
=
()
1
2
1
2
1
+
+
=
τ
α
τ
α
τ
ϑ
e
A
e
A
1)
1
>
ε
C
L
R
2
>
1
2
1
−
−
−
=
ε
ε
α
1
2
2
−
+
−
=
ε
ε
α
T
T
δ
ε
2
1
=
LC
RC
2
1
=
C
L
R
2
=
Posta
ć
ϑ
p
zale
ży
od
wsp
ół
cz
yn
ni
ka
ε
rozwi
ązan
ie
ap
er
io
dy
czn
e
6
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
(
)
1
0
2
1
+
+
=
A
A
ϑ
0
=
(
)
0
2
2
1
1
0
2
1
=
=
+
=
τ
τ
α
τ
α
τ
α
α
τ
ϑ
e
A
e
A
d
d
2
2
1
1
α
α
A
A
+
=
0
=
2
1
2
1
α
α
α
−
=
A
2
1
1
2
α
α
α
−
−
=
A
()
1
2
1
2
1
1
2
1
2
+
−
−
−
=
τ
α
τ
α
α
α
α
α
α
α
τ
ϑ
e
e
()
=
T
t
U
t
u
z
ϑ
z
T
t
z
T
t
z
U
e
U
e
U
+
−
−
−
=
2
1
2
1
1
2
1
2
α
α
α
α
α
α
1
1
α
T
T
=
2
2
α
T
T
=
7
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
()(
)
ωτ
ωτ
τ
ϑ
ετ
sin
cos
2
1
A
A
e
p
+
=
−
2)
1
0
<
<
ε
C
L
R
2
0
<
<
ω
ε
α
j
−
−
=
1
ω
ε
α
j
+
−
=
2
rozwi
ązan
ie
o
sc
ylac
yjn
e
tł
um
ione
2
1
ε
ω
−
=
(
)
(
)
1
sin
cos
2
1
+
+
=
−
ωτ
ωτ
τ
ϑ
ετ
A
A
e
(
)
1
0
1
+
=
A
ϑ
0
=
()
ωτ
ω
ωτ
ω
ετ
cos
sin
2
1
A
A
e
+
−
+
−
()
ωτ
ωτ
ε
τ
ϑ
ετ
sin
cos
2
1
A
A
e
d
d
+
−
=
−
1
1
−
=
A
8
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
2
1
0
A
A
d
d
ω
ε
τ
ϑ
τ
+
−
=
=
0
=
ω
ε
ω
ε
−
=
=
1
2
A
A
()
1
sin
cos
+
−
−
=
−
ωτ
ω
ε
ωτ
τ
ϑ
ετ
e
()
z
T
t
z
U
t
t
e
U
t
u
+
−
−
=
−
0
0
sin
cos
0
ω
ω
ε
ω
ε
T
T
=
0
T
ω
ω
=
0
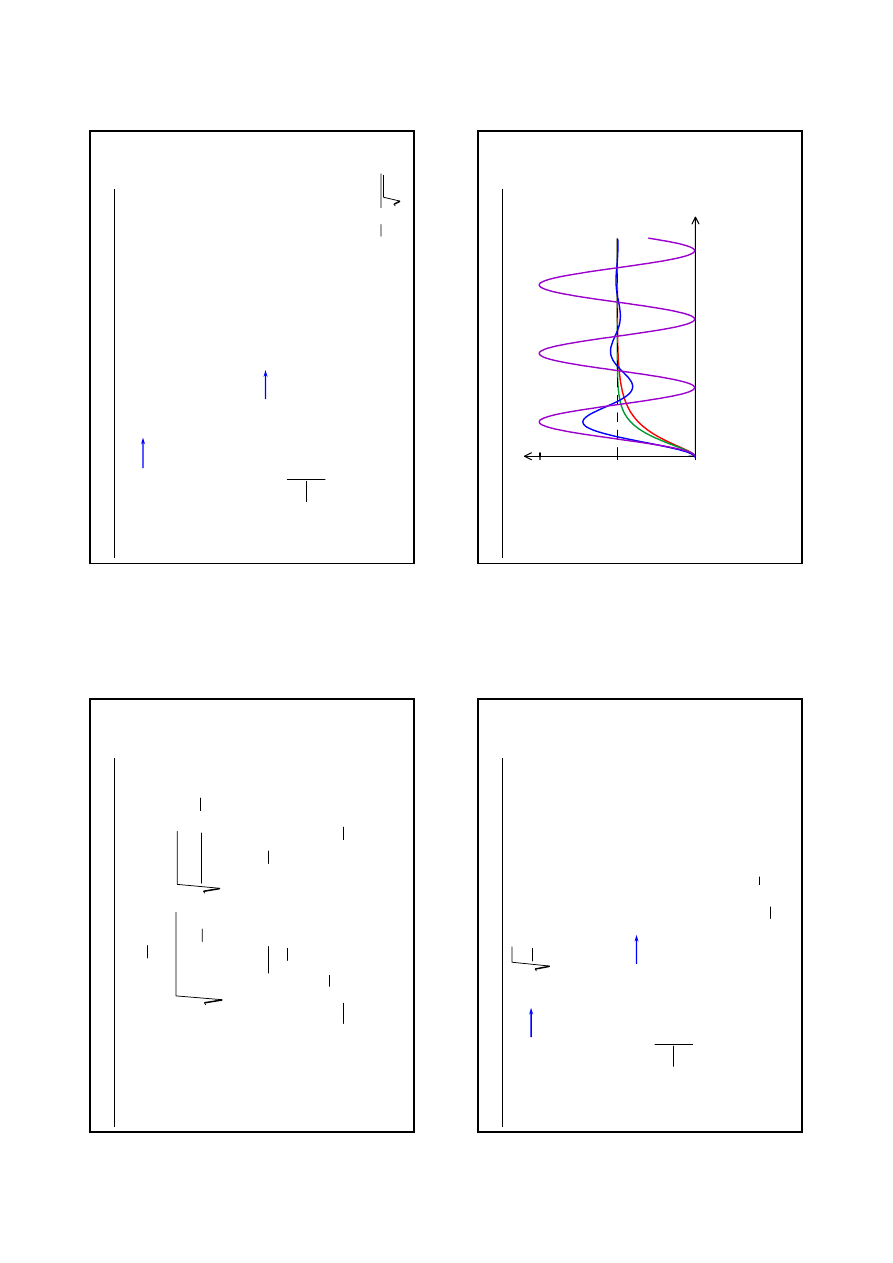
3
9
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
()
α
ω
β
ω
ω
ε
ω
+
=
−
−
t
t
t
0
0
0
sin
sin
cos
()
2
2
1
+
−
=
ω
ε
β
2
2
2
ω
ε
ω
+
=
ω
1
=
−
−
=
ω
ε
α
1
arctg
−
=
ε
ω
π
arctg
()
z
T
t
z
U
t
e
U
t
u
+
−
−
+
=
−
ε
ω
π
ω
ω
arctg
sin
0
0
10
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
()
τ
τ
τ
ϑ
sin
cos
2
1
A
A
p
+
=
3)
0
=
ε
0
=
R
rozwi
ązan
ie
o
sc
ylac
yjn
e
nie
tł
um
ione
1
=
ω
(
)
1
0
1
+
=
A
ϑ
0
=
()
0
2
1
0
cos
sin
=
=
+
−
=
τ
τ
τ
τ
τ
ϑ
A
A
d
d
1
1
−
=
A
(
)
1
sin
cos
2
1
+
+
=
τ
τ
τ
ϑ
A
A
2
A
=
0
=
(
)
1
cos
+
−
=
τ
τ
ϑ
()
z
z
U
t
U
t
u
+
−
=
0
cos
ω
LC
T
1
1
0
=
=
ω
11
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
()
(
)
τ
τ
τ
ϑ
−
+
=
e
A
A
p
2
1
4)
1
=
ε
C
L
R
2
=
rozwi
ązan
ie
ap
er
io
dy
czn
e
o t
łu
m
ie
niu kry
ty
cz
nym
(
)
1
0
1
+
=
A
ϑ
0
=
()
[
]
0
2
1
2
0
=
−
−
=
+
−
=
τ
τ
τ
τ
τ
τ
ϑ
e
A
A
e
A
d
d
1
1
−
=
A
1
2
A
A
−
=
0
=
()
(
)
1
2
1
+
+
=
−
τ
τ
τ
ϑ
e
A
A
1
1
2
−
=
=
A
A
()
(
)
1
1
+
−
−
=
−
τ
τ
τ
ϑ
e
()
z
T
t
z
U
e
T
t
U
t
u
+
+
−
=
−
1
12
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
C
t
u
(t
)
U
z
2U
z
ε
=1,
25
ε
=1
ε
=0,
25
ε
=0
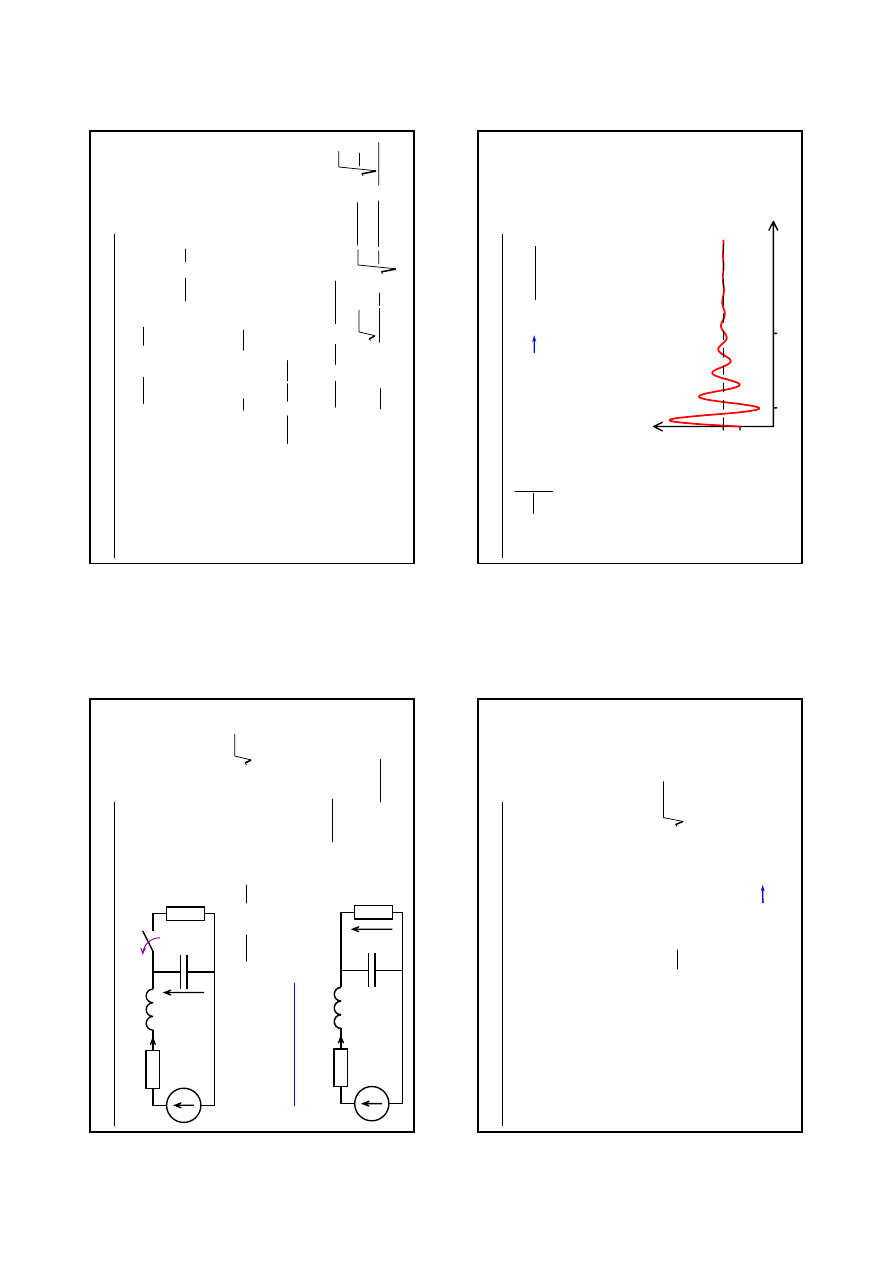
4
13
Wy
łą
czen
ie odbiornika pr
ądu sta
łego
R
L
U
z
C
z
U
u
dt
du
T
dt
u
d
T
=
+
+
δ
2
2
2
LC
T
=
RC
T
=
δ
R
0
Wa
ru
nk
i poc
zą
tkowe
R
U
z
I
U
t<0
R
0
0
R
R
U
I
z
+
=
0
0
0
R
R
U
R
I
R
U
z
+
=
=
i
u
t=0
()
0
i
=
(
)
0
u
=
14
Wy
łą
czen
ie odbiornika pr
ądu sta
łego
z
U
u
dt
du
T
dt
u
d
T
=
+
+
δ
2
2
2
()
U
u
=
0
()
()
C
I
C
i
u
=
=
′
0
0
zm
ie
nne
be
zw
ym
ia
rowe
:
T
t
=
τ
z
U
u
=
ϑ
1
2
2
=
+
+
ϑ
τ
ϑ
τ
ϑ
δ
d
d
T
T
d
d
pr
zesk
alo
w
an
e
równa
nie
pr
zesk
alo
w
an
e
wa
runk
i
poc
zą
tkowe
()
()
z
z
U
U
U
u
=
=
0
0
ϑ
()
()
0
0
u
U
T
z
′
=
′
ϑ
C
I
U
LC
z
=
z
z
U
R
R
U
C
L
0
+
=
0
R
R
C
L
+
=
0
0
R
R
R
+
=
15
Wy
łą
czen
ie odbiornika pr
ądu sta
łego
prz
yk
łado
w
e w
ar
to
śc
i liczbo
w
e:
R
=2,5
Ω
, R
0
=10
Ω
, L
=0,2 m
H
, C
=2
µF,
U
z
=120 V
T
=20
µs,
T
δ
=5
µs,
I=9,6 A,
U
=96 V
u(0
)=
96 V,
u’(
0)=
48
·10
5
V/s
ϑ
(0
)=
0,8,
ϑ
’(
0)
=
0,8
125,
0
2
=
=
T
T
δ
ε
0
<
992,
0
1
2
=
−
=
ε
ω
()(
)
1
sin
cos
2
1
+
+
=
−
ωτ
ωτ
τ
ϑ
ετ
A
A
e
(
)
1
0
1
+
=
A
ϑ
8,
0
=
2,
0
1
−
=
A
16
Wy
łą
czen
ie odbiornika pr
ądu sta
łego
2
1
0
A
A
d
d
ω
ε
τ
ϑ
τ
+
−
=
=
8,
0
=
781,
0
8,
0
1
2
=
+
=
ω
εA
A
()
(
)
1
992.
0
sin
781,
0
992,
0
cos
2,
0
125,
0
+
+
−
=
−
τ
τ
τ
ϑ
τ
e
(
)
1
36,
14
992,
0
sin
806,
0
125,
0
+
−
=
−
o
τ
τ
e
()
(
)
[
]
V
120
36,
14
49600
sin
72,
96
6250
+
−
=
−
o
t
e
t
u
t
0.
1
0.
5
t[ms
]
96
12
0
u
[V
]
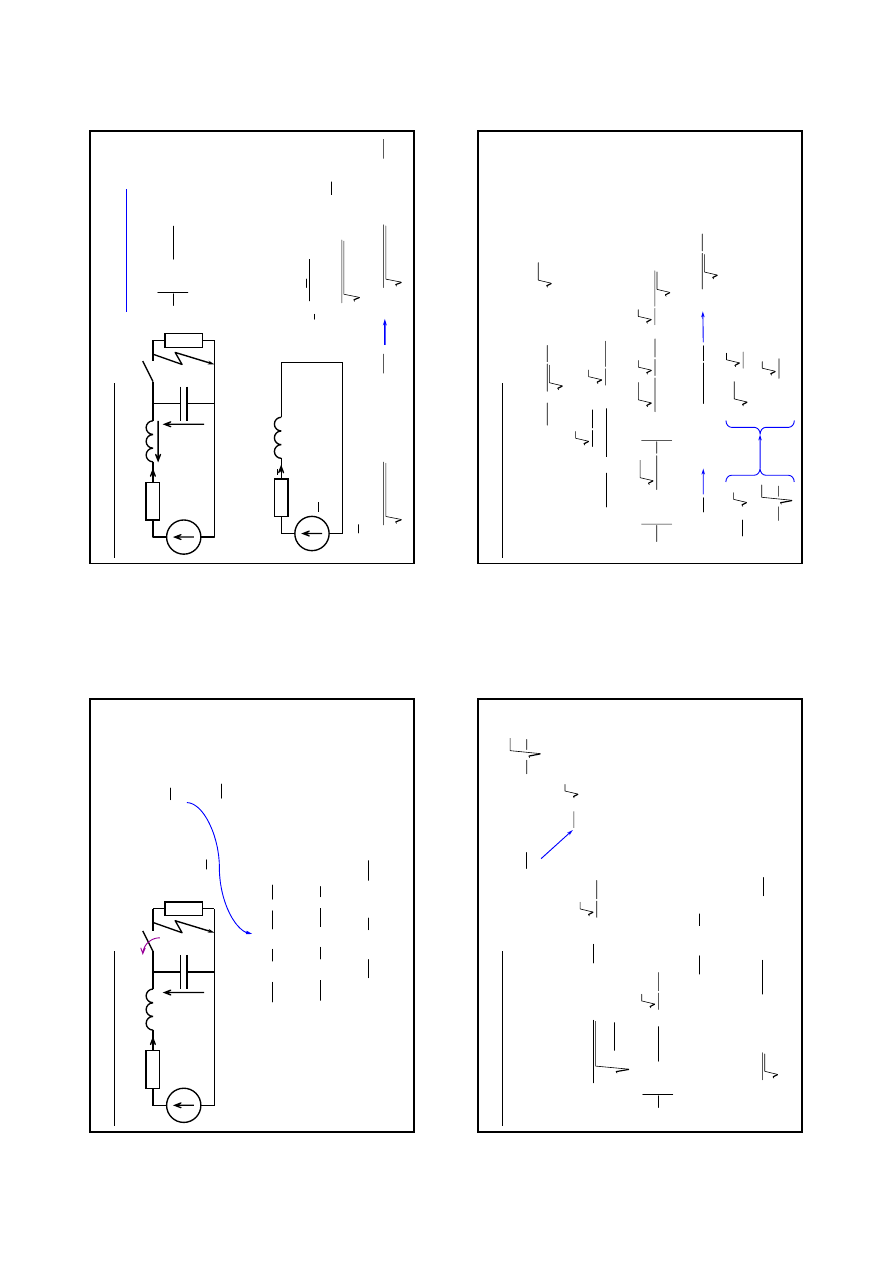
5
17
Wy
łą
czen
ie zwarcia
i
u
t=0
(
)
ϕ
ω
+
=
t
U
u
m
z
sin
0
=
−
−
−
u
dt
di
L
Ri
u
z
dt
du
C
i=
0
=
−
−
−
u
u
u
u
L
R
z
0
2
2
=
−
−
−
dt
du
dt
i
d
L
dt
di
R
dt
du
z
dt
d
0
2
2
=
−
−
−
C
i
dt
i
d
L
dt
di
R
dt
du
z
dt
du
C
i
dt
di
RC
dt
i
d
LC
z
=
+
+
2
2
(
)
ϕ
ω
ω
+
=
t
C
U
m
cos
C
R
L
u
z
(t
)
R
0
18
Wy
łą
czen
ie zwarcia
R
L
u
z
(t
)
C
i
u
t=0
(
)
ϕ
ω
+
=
t
U
u
m
z
sin
(
)
L
u
dt
di
L
t
+
=
=
+
0
0
(
)
(
)
(
)
(
)
+
+
+
+
+
+
=
0
0
0
0
u
u
Ri
u
L
z
()
0
i
(
)
ϕ
sin
0
m
z
U
u
=
+
(
)
()
0
0
i
i
=
+
(
)
0
0
=
+
u
L
j
R
U
I
z
ω
+
=
Wa
ru
nk
i poc
zą
tkowe
()
0
i′
R
ω
L
U
z
I
t<0
−
+
=
R
L
arctg
2
2
2
ω
ϕ
ω
j
m
e
L
R
U
ϕj
m
z
e
U
U
=
()
−
+
+
=
R
L
arctg
sin
2
2
2
ω
ϕ
ω
ω
t
L
R
U
t
i
m
()
−
+
=
R
L
arctg
sin
0
2
2
2
ω
ϕ
ω
L
R
U
i
m
(
)
()
0
sin
0
Ri
U
u
m
L
−
=
+
ϕ
R
0
t<0
u
L
19
Wy
łą
czen
ie zwarcia
Prz
yk
łado
w
e w
ar
to
ści
0
=
ϕ
o
60
arctg
=
R
L
ω
C
L
R
20
1
=
t
C
U
i
dt
di
RC
dt
i
d
LC
m
ω
ω
cos
2
2
=
+
+
()
−
+
=
R
L
arctg
sin
1
0
2
2
2
ω
ω
R
L
R
U
i
m
3
=
R
L
ω
R
U
m
4
3
−
=
()
L
Ri
dt
di
t
0
0
−
=
+
=
L
U
m
4
3
=
zm
ie
nne
be
zw
ym
ia
rowe
LC
t
=
τ
C
U
i
m
ω
ϑ
=
m
U
u
=
σ
20
Wy
łą
czen
ie zwarcia
τ
ω
ϑ
τ
ϑ
τ
ϑ
LC
d
d
LC
RC
d
d
cos
2
2
=
+
+
równanie bezwy
m
iarowe
()
()
C
U
i
m
ω
ϑ
0
0
=
C
U
R
U
m
m
ω
4
3
−
=
RC
ω
1
4
3
−
=
+
+
=
=
=
0
0
t
m
dt
di
C
U
LC
d
d
ω
τ
ϑ
τ
L
U
C
U
LC
m
m
4
3
ω
=
LC
ω
1
4
3
=
dt
du
C
i=
(
)
dt
d
d
U
d
C
C
U
m
m
τ
τ
σ
ω
ϑ
=
τ
σ
ω
ϑ
d
d
LC
1
=
C
L
R
20
1
=
3
=
R
L
ω
20
3
=
LC
ω
400
3
=
RC
ω
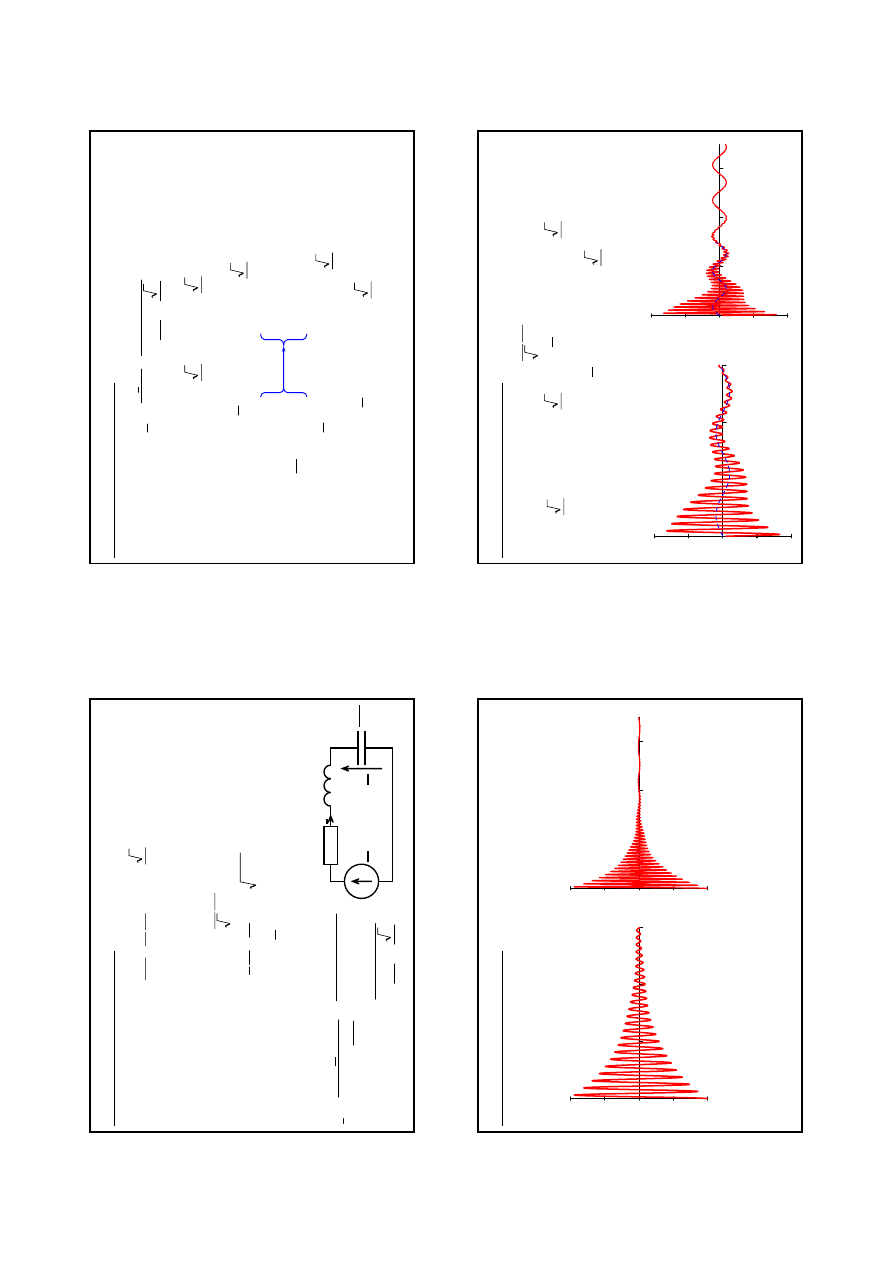
6
21
Wy
łą
czen
ie zwarcia
()
100
0
−
=
ϑ
()
5
0
=
′
ϑ
τ
σ
ϑ
d
d
3
20
=
τ
ϑ
τ
ϑ
τ
ϑ
20
3
cos
20
1
2
2
=
+
+
d
d
d
d
40
1
20
1
2
1
=
=
ε
1
1
2
≈
−
ε
()
()
τ
τ
τ
ϑ
τ
sin
cos
2
1
40
A
A
e
p
+
=
−
R
1
.
ω
C
U
sk
ła
dowa
wy
m
usz
ona
ω
L
U
z
I
w
C
j
L
j
R
U
I
z
w
ω
ω
1
+
+
=
RC
j
LC
C
j
U
m
ω
ω
ω
+
−
=
2
1
400
3
400
3
1
j
C
j
U
m
+
−
=
ω
22
Wy
łą
czen
ie zwarcia
400
3
400
3
1
j
j
C
U
I
m
w
w
+
−
=
=
Θ
ω
1j
≈
()
=
+
=
τ
τ
τ
ϑ
20
3
cos
90
20
3
sin
w
90
1
j
e
=
()
()
+
+
=
−
τ
τ
τ
τ
ϑ
τ
20
3
cos
sin
cos
2
1
40
A
A
e
()
100
1
0
1
−
=
+
=
A
ϑ
()
5
40
1
0
2
1
=
+
−
=
′
A
A
ϑ
101
1
−
=
A
525,
7
2
=
A
()
()
+
+
−
=
−
τ
τ
τ
τ
ϑ
τ
20
3
cos
sin
525.
7
cos
101
40
e
()
+
−
=
−
τ
τ
τ
20
3
cos
7,
85
sin
3,
101
40
o
e
23
Wy
łą
czen
ie zwarcia
prz
eb
ie
g pr
ądu
0
5
0
100
150
τ
-100
-50
0
50
100
0
100
200
30
0
τ
-100
-50
0
50
100
24
Wy
łą
czen
ie zwarcia
()
+
−
=
−
τ
τ
τ
20
3
sin
1,
177
sin
77,
8
40
o
e
τ
σ
ϑ
d
d
3
20
=
()
()
0
20
3
0
σ
τ
τ
ϑ
σ
τ
+
=
∫
d
()
0
20
3
cos
7,
85
sin
3,
101
20
3
0
40
+
+
−
=
∫
−
τ
τ
τ
τ
τ
d
e
o
prz
eb
ie
g na
pi
ęcia
0
5
0
100
150
τ
-10
-5
0
5
10
0
100
200
30
0
τ
-10
-5
0
5
10
Wyszukiwarka
Podobne podstrony:
PE EN st p
bilans pe en, Rachunkowość
PE EN Obwody 3 f
Josip Jurčič Telečja pečenka
Wyznaczanie stężenia nasycenia substancji reaktywnych (8), 1. 13 WYZNACZANIE ST??ENIA NASYCENIA SUBS
EMMS ST EN
ST 30 Dry contact EN
Dane porównawcze ASME i EN dla testów mechanicznych Authors of Elmar Upitis, PE and Michael Gold
Blaupunkt St Louis C32 EN Manual
MT st w 06
cukry cz 2 st
Szacowanie zasobów st
Żywienie sztuczne niem St
ch zwyrodnieniowa st
Zaj III Karta statystyczna NOT st
więcej podobnych podstron