1
Podstawy elektrotechniki
2
Stan ustalony i stan przej
ściowy
Stan ustalony
W o
bwodz
ie
pr
ądu sta
łeg
o
W o
bwodz
ie
pr
ądu zm
ie
nne
go
•W
ar
to
ści
p
rą
dó
w i na
pi
ęć
ni
e uleg
aj
ą
zm
ia
nie
•W
ar
to
ści
ś
re
dn
ie i sk
ut
eczn
e p
rą
dów i na
pi
ęć
nie
ule
ga
ją
zm
ianie
•P
rą
dy
i
na
pi
ęcia s
ą
funkc
ja
m
i okre
sow
ym
i o ta
kie
j sa
m
ej
cz
ęstotl
iwo
ści, jak
cz
ęs
to
tli
wo
ść
wy
m
uszen
ia
Stan nieustalony
(przej
ściowy
)
•P
rą
dy
i
na
pi
ęcia s
ą
nieokresowy
m
i funkcjam
i czasu
3
Stan ustalony i stan przej
ściowy
Czy
nn
iki wy
w
oł
uj
ące stan
nieu
stalo
ny
•
P
ro
cesy
łą
czen
io
we (
zm
ian
a st
ru
ktury
ob
wo
du
, k
om
ut
acja)
•
Z
m
ia
ny
pa
ram
etrów e
le
m
en
tó
w obwodu
→
zm
iany pozy
cji
łą
czników,
→
wyst
ępow
an
ie
zwar
ć
i p
rzerw w obwodzie (uszkod
zeni
a, praca
bezpi
eczników),
→
inne czynn
oś
ci
łą
czeniow
e,
→ź
ród
ła
: zm
ia
na
n
api
ęcia,
c
zę
stotliwo
ści ,
f
azy
→
elem
enty bierne: zm
ian
a rezyst
ancji, indukcyjno
ści, pojem
no
ści,
zm
ian
a char
akt
er
ystyki
→
wy
ładow
ania at
m
osf
er
yczne.
4
Stan przej
ściowy (nieustalony)
)
(
)
(
)
(
t
i
t
i
t
i
w
p
+
=
Pr
ąd w sta
nie
pr
zej
ścio
w
ym
Sk
ła
dowa
pr
zej
ścio
w
a
Sk
ła
dowa
wy
m
usz
ona
0
)
(
→
∞
→t
p
t
i
)
(
)
(
t
i
t
i
w
t
→
∞
→
W o
bwodz
ie
pr
ądu sta
łe
go l
ub
sin
uso
ida
lne
go
:
)
(
)
(
t
i
t
i
u
w
=
Sk
ła
dowa
usta
lona
S
tan
nieu
stalo
ny
jest pr
zej
ście
m
obwodu z doty
chczasowego
stanu
usta
lone
go d
o n
owe
go sta
nu us
ta
lo
ne
go
2
5
Warunki ci
ąg
ło
ści
Dla
t=
t
0
:
)
(
lim
)
(
lim
0
0
t
i
t
i
t
t
t
t
+
−
→
→
=
)
(
)
(
0
0
+
−
=
t
i
t
i
Dla
t=
t
0
:
)
(
lim
)
(
lim
0
0
t
u
t
u
t
t
t
t
+
−
→
→
=
)
(
)
(
0
0
+
−
=
t
u
t
u
Pr
ąd i
nd
ukc
yjn
oś
ci
je
st
f
unkc
ją
ci
ąg
łą
Napi
ęcie k
on
de
ns
ator
a jest
funkc
ją
ci
ąg
łą
L
i
C
u
En
er
gia zawar
ta
w p
ol
u mag
ne
ty
czny
m
ce
wk
i lub
p
olu
ele
ktry
czn
ym
ko
nde
nsa
tora
n
ie
m
oż
e ule
c zmia
nie
w spos
ób
sko
kow
y.
2
2
Li
E
=
2
2
Cu
E
=
6
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
0
=
−
−
dt
di
L
Ri
U
z
w
p
i
i
i
+
=
Ró
wn
an
ie ch
arak
tery
sty
czn
e:
L
U
i
L
R
dt
di
z
=
+
równa
nie
ró
żnicz
kowe
I rz
ędu
liniowe o sta
łych wspó
łczy
nnikach
ca
łk
a ogólna równania
jednorodnego
ca
łka
s
zcz
eg
ól
na
ró
w
na
ni
a
niejednorodnego
0
=
+
L
R
r
L
R
r
−
=
ca
łka
ogó
ln
a:
t
L
R
p
Ae
i
−
=
pr
zewidy
w
an
a ca
łk
a szczeg
ól
na:
I
i
w
=
A
–s
ta
ła ca
łkow
an
ia
R
L
U
z
t=
0
i
0
=
−
−
L
R
z
u
u
U
7
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
po p
ods
ta
wie
ni
u
I
do r
ówna
nia
:
L
U
I
L
R
dt
dI
=
+
roz
w
ią
za
nie
og
ól
ne
:
R
U
Ae
i
t
L
R
+
=
−
wa
rune
k poc
zą
tkow
y:
R
U
i
w
=
0=
L
R
L
U
I
=
R
U
=
Z ci
ąg
ło
ści
p
rą
du w in
du
kc
yj
no
ści:
)
0(
)
0(
+
−
=
i
i
0
)
0(
=
−
i
0
)
0(
=
+
i
)0
(i
=
0
)0
(
=
i
T
R
L
=
-s
ta
ła cz
asow
a pr
ze
biegu
pr
zej
ściow
ego
R
U
Ae
i
T
t
+
=
−
8
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
Ro
zwi
ązan
ie:
()
R
U
e
R
U
t
i
z
T
t
z
+
−
=
−
z r
ozwi
ązan
ia o
gó
ln
ego
:
R
U
Ae
z
+
=
0
0
R
U
A
z
−
=
−
=
−
T
t
z
e
R
U
1
R
U
z
R
U
z
−
t
T
R
U
e
R
U
z
z
T
t
+
−
−
T
t
e
R
U
z
−
T
t
e
R
U
z
−
−
3
9
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
L
U
i
L
R
dt
di
z
=
+
R
L
R
U
i
dt
di
R
L
z
=
+
T
i
w
sta
ła czasow
a przebiegu
pr
zej
ściow
ego
sk
ładowa wy
m
us
zona w
obwodzi
e pr
ądu sta
łego
T
t
Ae
−
i
p
sk
ładowa przej
ścio
w
a
w obwodzie I rz
ędu
10
W
łą
czenie napi
ęcia sta
łego do ga
łę
zi R
L
Ri
u
R
=
dt
di
L
u
L
=
−
=
−
T
t
z
e
R
U
R
1
−
=
−
T
t
z
e
U
1
−
=
−
T
t
z
e
R
U
dt
d
L
1
T
t
z
e
T
U
R
L
−
=
1
T
t
z
e
U
−
=
T
t
u
R
u
L
U
z
11
Ł
adowanie kondensatora
()
0
0
=
u
0
=
−
−
u
Ri
U
z
dt
du
C
i=
z
U
u
dt
du
RC
=
+
T
w
p
u
u
u
+
=
Sk
ła
dowa
prz
ej
ścio
w
a:
T
t
Ae
t
u
p
−
=
)
(
roz
w
ią
za
nie
og
ól
ne
:
z
U
Ae
t
u
T
t
+
=
−
)
(
0
)0
(
0
=
+
=
z
U
Ae
u
z
U
A
−
=
0
=
−
−
u
dt
du
RC
U
z
w
u
z wa
runków po
cz
ątkow
yc
h:
z
z
U
e
U
t
u
T
t
+
−
=
−
)
(
t =0
R
C
U
z
u
i
12
Ł
adowanie kondensatora
dt
du
C
i=
(
)
z
z
U
e
U
dt
d
C
T
t
+
−
=
−
T
t
e
RC
CU
z
−
−
−
=
1
T
t
e
R
U
z
−
=
R
U
z
t
T
z
z
U
e
U
t
u
T
t
+
−
=
−
)
(
z
U
0
u
,
i
4
13
Wy
łą
czen
ie napi
ęcia zasilaj
ącego
0
2
1
=
+
+
i
R
i
R
dt
di
L
T
t
Ae
t
i
p
−
=
)
(
2
1
R
R
L
T
+
=
0
)
(
=
t
i
w
T
t
Ae
t
i
−
=
)
(
R
1
L
U
z
R
2
2
1
R
R
α
=
()
0
2
1
=
+
+
i
R
R
dt
di
L
0
2
1
=
+
+
i
dt
di
R
R
L
T
()
2
1
R
L
α
+
=
t=
0
i
14
Wy
łą
czen
ie napi
ęcia zasilaj
ącego
2
R
U
A
z
=
Wa
rune
k poc
zą
tkow
y
2
)
0(
R
U
i
z
=
−
.
const
I
i
=
=
2
)
0(
)
0(
R
U
i
i
z
=
=
−
+
T
t
e
R
U
t
i
z
−
=
2
)
(
R
1
L
U
z
R
2
i
0
=
=
dt
di
L
u
L
t<
0
stan us
tal
on
y
(obwó
d pr
ądu s
ta
łego
)
z
U
u
u
=
=
2
1
z ci
ąg
ło
ści p
rą
du
w ind
ukc
yjn
oś
ci:
()
T
Ae
i
0
0
−
+
=
u
2
u
1
u
L
15
Wy
łą
czen
ie napi
ęcia zasilaj
ącego
L
R
1
U
z
R
2
i
)
(
)
(
1
1
t
i
R
t
u
=
T
t
e
R
U
R
z
−
=
2
2
α
T
t
e
U
t
u
z
−
=
α
)
(
1
z
U
t
u
t
u
+
=
)
(
)
(
1
0
dt
di
L
t
u
L
=
)
(
T
t
e
T
R
U
L
z
−
−
=
1
2
()
T
t
e
U
t
u
z
L
−
+
−
=
α
1
)
(
z
z
U
e
U
T
t
+
=
−
α
()
T
t
e
R
L
R
U
L
z
−
+
−
=
2
2
1
1
α
z
U
t
T
dla
α
=10
z
U
11
−
z
U
10
z
U
11
u
0
(t
)
u
1
(t
)
u
L
(t
)
u
1
u
L
u
0
16
W
łą
czenie odbiornika
R
C
U
z
R
0
0
R
R
α
=
Zasto
so
w
anie tw. Th
ev
en
in
a
R
U
z
R
0
0
0
R
R
R
U
U
z
T
+
=
1
1
+
=
α
z
U
R
R
0
0
0
R
R
RR
R
T
+
=
1
0
+
=
α
α
R
u
t =0
U
T
R
T
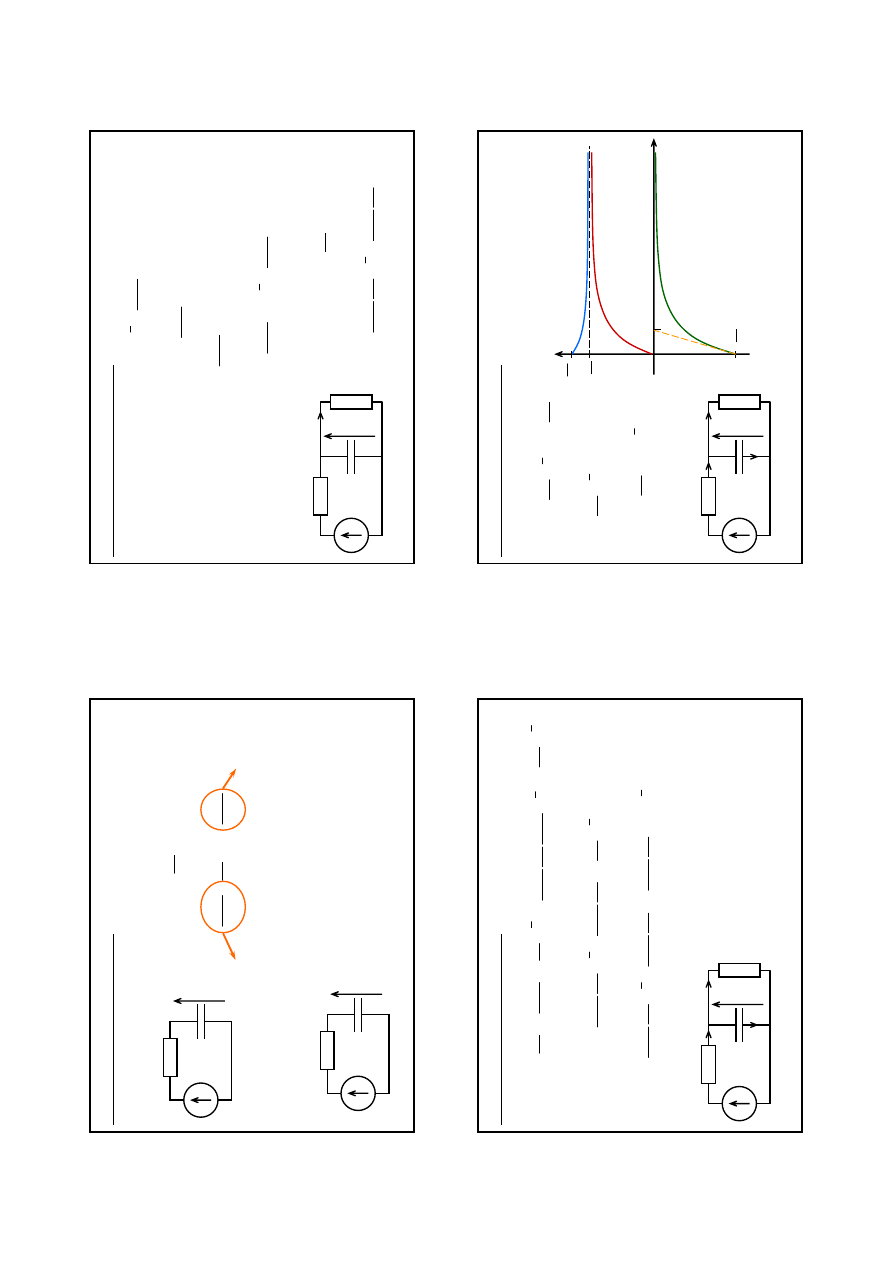
5
17
W
łą
czenie odbiornika
R
T
C
U
T
S
ch
em
at zast
ęp
czy
dla t
≥0
T
T
U
u
dt
du
C
R
=
+
T
w
u
1
1
0
+
=
+
+
α
α
α
z
U
u
dt
du
C
R
R
C
U
z
Sc
hem
at dla
t<
0
Wa
rune
k poc
zą
tkow
y
()
z
U
u
=
−
0
Z ci
ąg
ło
ści
n
ap
ię
cia:
)
0(
)
0(
+
−
=
u
u
z
U
u
=
)0
(
u
u
18
W
łą
czenie odbiornika
Ro
zwi
ązan
ie o
gó
ln
e:
z
U
=
1
)
(
+
+
=
−
α
z
U
Ae
t
u
T
t
1
)0
(
+
+
=
α
z
U
A
u
z
U
A
1
+
=
α
α
Ro
zwi
ąz
anie
ko
ńco
we:
1
1
)
(
+
+
+
=
−
α
α
α
z
z
U
e
U
t
u
T
t
R
C
U
z
R
0
0
0
)
(
R
u
t
i
=
0
0
1
1
1
R
U
e
R
U
z
z
T
t
+
+
+
=
−
α
α
α
u
i
0
19
W
łą
czenie odbiornika
R
C
U
z
u
R
0
i
0
dt
du
C
t
i
=
)
(
T
t
e
T
U
z
−
−
+
=
1
1
α
α
T
t
e
R
U
z
−
+
+
−
=
α
α
α
α
1
1
0
T
t
e
R
U
z
−
−
=
0
0
i
i
i
R
+
=
0
0
1
1
1
R
U
e
R
U
z
z
T
t
+
+
+
=
−
α
α
α
T
t
e
R
U
z
−
−
0
0
0
1
1
1
1
R
U
e
R
U
z
z
T
t
+
+
+
−
=
−
α
α
−
+
=
−
T
t
e
R
U
z
1
1
1
0
α
i
R
i
20
W
łą
czenie odbiornika
R
C
U
z
u
R
0
i
0
i
R
i
0
0
0
8,
0
2,
0
R
U
e
R
U
i
z
z
T
t
+
=
−
T
t
e
R
U
i
z
−
−
=
0
−
=
−
T
t
e
R
U
i
z
R
1
8,
0
0
t
T
0
8,
0
R
U
z
0
R
U
z
0
R
U
z
−
dla
α
=0,25
i
0
i
i
R
Wyszukiwarka
Podobne podstrony:
PE EN st p 2
bilans pe en, Rachunkowość
PE EN Obwody 3 f
Josip Jurčič Telečja pečenka
Wyznaczanie stężenia nasycenia substancji reaktywnych (8), 1. 13 WYZNACZANIE ST??ENIA NASYCENIA SUBS
EMMS ST EN
ST 30 Dry contact EN
Dane porównawcze ASME i EN dla testów mechanicznych Authors of Elmar Upitis, PE and Michael Gold
Blaupunkt St Louis C32 EN Manual
MT st w 06
cukry cz 2 st
Szacowanie zasobów st
Żywienie sztuczne niem St
ch zwyrodnieniowa st
Zaj III Karta statystyczna NOT st
więcej podobnych podstron