
Kilka zadań z linii długiej z wynikami
Zad. 1. Powietrzna linia bezstratna przy
100 000
ω
=
1/s posiada impedancję falową
600
f
Z
Ω
Ω
Ω
Ω
=
. Wyznaczyć parametry jednostkowe linii.
Odp.
5, 55
C
=
pF/m,
2 µH/m
L
=
Zad. 2. Linia długa ma przy częstotliwości
800
f
=
MHz następujące parametry:
75
f
Z
Ω
Ω
Ω
Ω
=
,
0, 01
α
=
1/m,
21
β
=
1/m,
0
G
=
. Obliczyć parametry jednostkowe
,
,
L C R oraz prędkość fazową
f
v .
Odp.
8
1,5 Ω/m,
0,313µH/m,
55,8 pF/m,
2.39 10 m/s
f
R
L
C
v
=
=
=
=
⋅
Zad. 3. Dana jest bezstratna linia długa o parametrach jednostkowych
4
1, 67 10
L
−
=
⋅
H/km,
66, 7
C
=
nF/km. Zespolone wartości skuteczne napięcia i prądu na
końcu linii wynoszą:
0
27
10
j
k
U
e
−
=
V,
0
25
0,125
j
k
I
e
==
A. Obliczyć współczynnik
odbicia na końcu linii
k
ΓΓΓΓ
, wartości chwilowe napięcia i prądu na początku linii oraz
impedancję wejściową
we
Z
.
Długość linii
92, 48
l
=
cm,
715
f
=
MHz.
Odp.
(
)
0
5
56 50'
50 Ω,
3 10 km/s,
49, 2
63 Ω,
0, 535
j
k
k
f
f
Z
v
Z
j
e
ΓΓΓΓ
−
=
= ⋅
=
−
=
Zad. 4. Linia bez strat o długości
100
l
=
m,
200
f
Z
Ω
Ω
Ω
Ω
=
,
3
22, 9 10
j
j
γ
β
−
=
=
⋅
1/m
obciążona jest rezystancją
100
k
R
Ω
Ω
Ω
Ω
=
. Obliczyć impedancję wejściową.
Odp.
0
36
216
j
wej
Z
e
−
=
Ω
Ω
Ω
Ω
Zad. 5.
Linię bezstratną o parametrach
60 ,
2,1
/
f
Z
rd m
β
=
Ω
=
, obciążono impedancją
0
30
100
.
j
k
Z
e
−
=
Ω
Jaka powinna być długość linii, by impedancja wejściowa
Wej
Z
była
rzeczywista? Jaka jest jej wartość?
Odp.
1
2
27,8 ,
129
Wej
Wej
Z
Z
≈
Ω
≈
Ω
Zad. 6.
Bezstratną linię długą o parametrach
240 ,
f
f
Z
v
c
=
Ω
=
obciążono impedancją
(70
10) .
k
Z
j
=
+
Ω
Długość linii
10 ,
l
m
=
częstotliwość
225 MHz
f
=
. Obliczyć impedancję
wejściową
Wej
Z
oraz współczynnik fali stojącej w linii.
Odp.Linia półfalowa.
(
)
1
70 10 j
,
3, 43
1
k
wej
k
Z
wfs
+
=
+
=
=
−
ΓΓΓΓ
Ω
Ω
Ω
Ω
ΓΓΓΓ
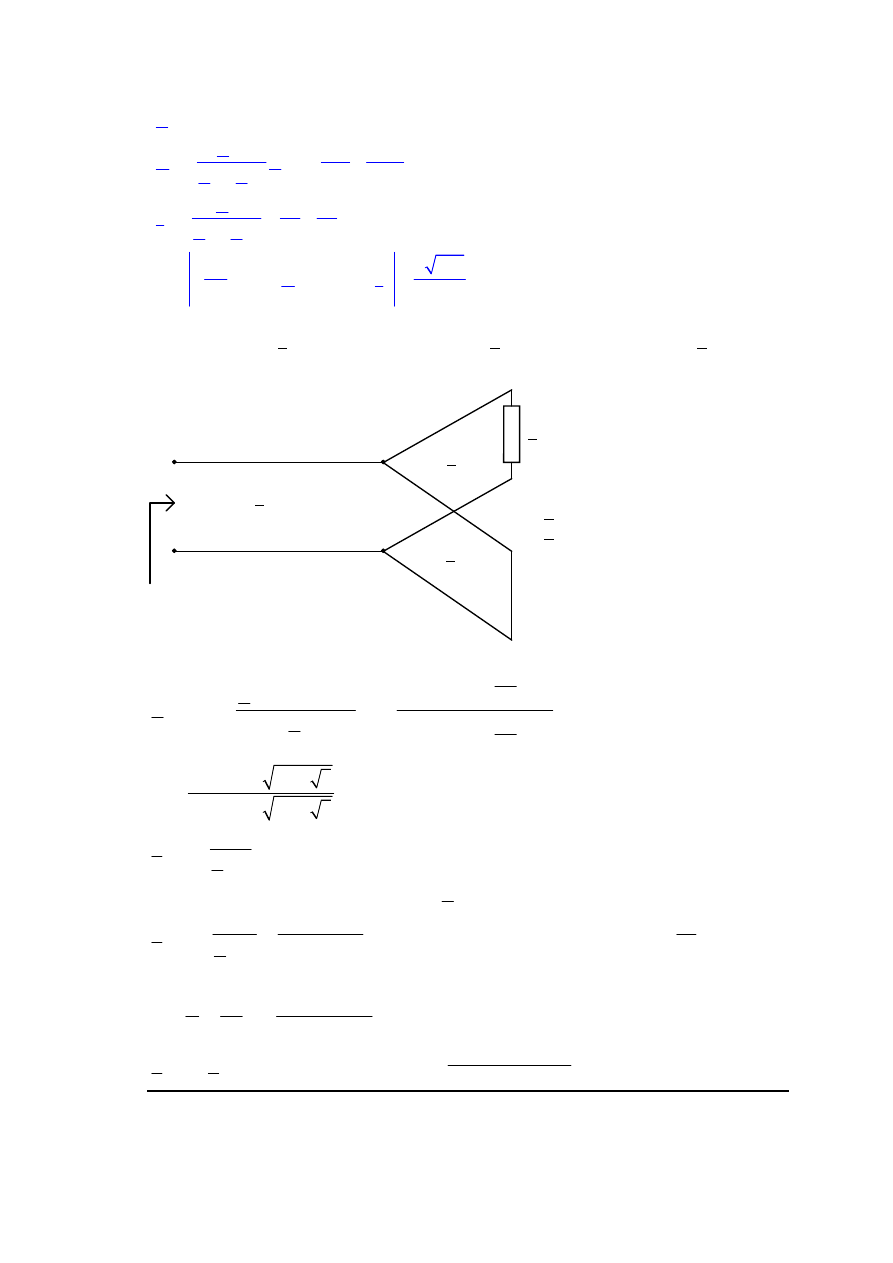
Zad. 7. Bezstratną linię długą zwarto na końcu. Obliczyć wartość skuteczną prądu I
k
.
Dane:
3 ,
1.875
,
75,
60
80 ,
100
g
g
f
m l
m Z
Z
j
E
V
λ
=
=
=
=
−
Ω
=
I
k
l
Z
g
E
g
Z
f
R
Odp.
( )
75j
,
300
3600
j
-10,34+124,13V
29
29
48
4
j 1,66+0,138jA
29
29
j
4 485
sin(
)
cos(
)
1.17A
75
wej
wej
g
p
g
wej
g
p
g
wej
p
p
k
f
Z
Z
U
E
Z
Z
E
I
Z
Z
I
l U
l I
Z
β
β
=
=
= −
+
≈
+
=
=
+
≅
+
= −
+
=
≅
Ω
Ω
Ω
Ω
Zad. 8. Dobrać l
x
i Z
x
tak, aby w linii o impedancji Z
x
nie wystąpiła fala stojąca, tj
Γ
x
=0, linie są
bezstratne.
Z
x
Z
f
l
l
x
Z
f
Γ
x
=0
Z
f
=50
Ω
Z
k
=200
Ω
l=0.1
λ
t
Z
k
Rozwiązanie
( )
( )
1
2
200
50
01
50
2
50
200
01
200
50 5
2 5
50
32.35004014-57.68759336j
50
200 5
2 5
π
λ
β
λ
π
β
λ
λ
+
+
=
=
+
+
+
−
=
≈
+
−
f
k
f
wej
f
k
j
tg
Z
jZ tg
l
Z
Z
Z
jZ tg
l
j
tg
j
j
1
1
1
0.007395336956+0.01318759387j
wej
wej
Y
Z
=
≈
Impedancja odcinka zwartego na końcu
(
)
2
f
x
wej
Z
jZ tg
l
β
=
a admitancja
(
)
(
)
2
2
1
1
f
x
wej
f
x
wej
Y
jY ctg
l
Z
jZ tg
l
β
β
=
=
= −
, czyli
1
-0.01318759387=-
( )
50
ctg x , stąd
x = .9878555317+k
π
. Ponieważ
x
x
l
β
=
, stąd
.9878555317
0.157222
2
2
x
x
x
l
λ
λ
λ
β
π
π
=
=
=
≈
.
x
1
2
1
.007395336956
Z
135.2
0.007395336956
wej
wej
Y
Y
+
=
→
=
=
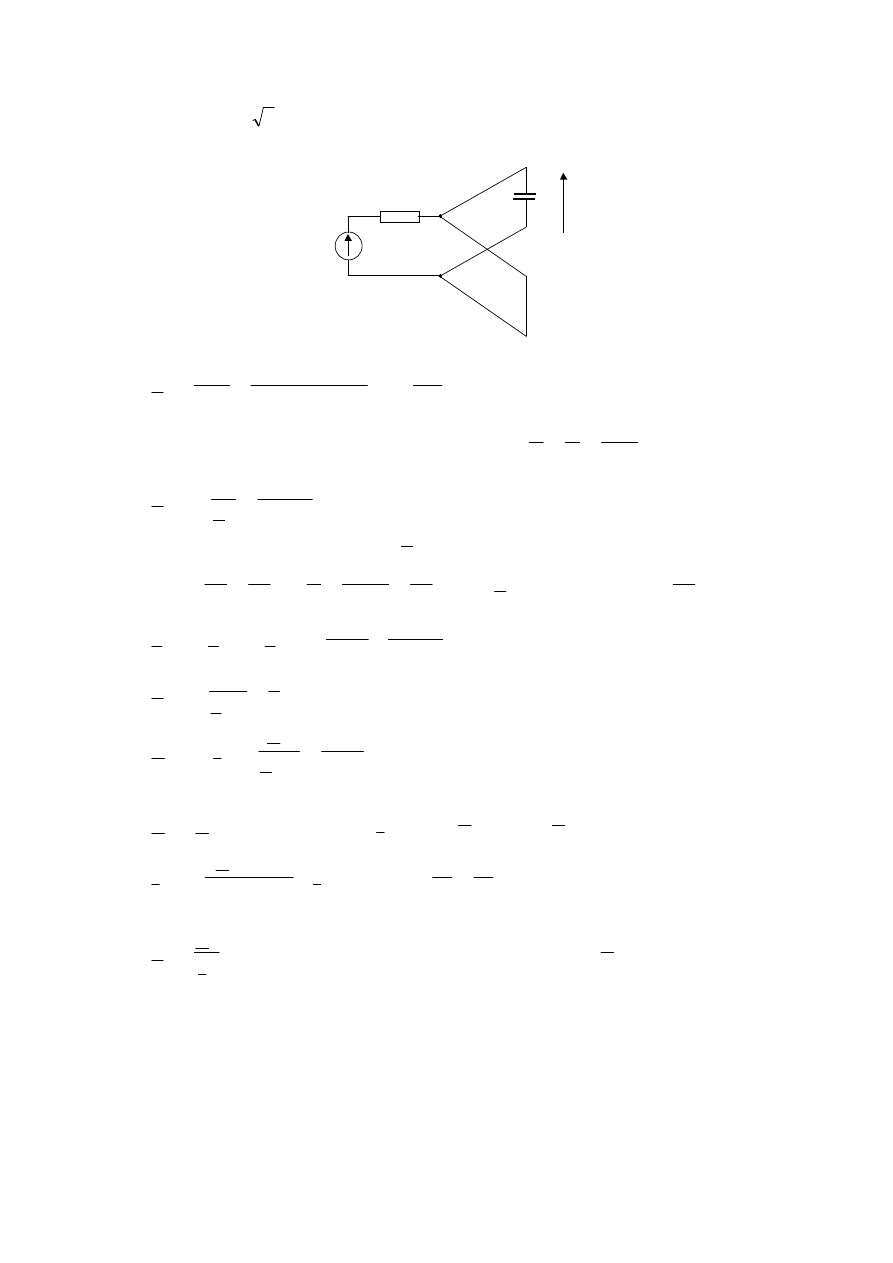
Zad. 9. Obliczyć napięcie u(t) na kondensatorze C
k
w układzie linii bezstratnych.
Dane: e(t) =
2
cos(2
π
10
8
t) [V], Z
f
=50
Ω
, R
g
= 50
Ω
, l = 0.75 m, C
k
= 20 pF, l
z
=
1.231575602 m.
l
lz
Zf
Zf
Ck
e(t)
Rg
U(t)
Rozwiązanie
8
12
1
1
250
79.5
2 10 2010
k
Z
j
j
j C
j
ω
π
π
−
=
=
= −
≈ −
Linia o długości l jest linią ćwierć falową(
8
8
310
3
10
c
T
f
f
υ
λ
υ
=
=
=
=
= ), zatem
2
2
1
50
31.5
79.5
f
wej
k
Z
Z
j
Z
j
=
=
≈
−
.
Impedancja linii zwartej na końcu
2
(
)
50 (1.231575 )
f
z
wej
Z
jZ tg
l
j
tg
β
β
=
=
,
ale
8
8
2
2
2 10
2
3
310
f
f
v
c
π
π
ω
π
π
β
λ
=
=
=
=
=
, zatem
2
2
50 (1.231575
)
31.5
3
wej
Z
j
tg
j
π
=
≈ −
1
2
1
1
0
31.5
31.5
1
1
0
wyp
wej
wej
wyp
wyp
Y
Y
Y
j
j
Z
Y
=
+
=
+
≈
−
=
=
= ∞
.
1
1
,
0.03175
31.5
p
p
p
wej
U
j
U
j I
Z
j
≈
=
=
=
.
Napięcie oraz prąd
cos(
)
sin(
)
cos( )
50 sin( ) 0.03175
1.5875
2
2
sin(
)
1
cos(
)
50
50
f
p
k
p
p
k
p
f
U
U
l
jZ
l I
j
j
j
jU
l
j
I
I
l
j
Z
π
π
β
β
β
β
=
−
=
−
= −
= −
+
= −
=
Sprawdzenie
79.5
k
k
k
U
Z
j
I
=
= −
. Ostatecznie
8
( )
2.2345sin(2 10
)
2
k
u t
t
π
π
=
−
Czesław Michalik
27.12.2006
Wyszukiwarka
Podobne podstrony:
zadanie rok 2 linia dluga
Zadania 4 (wyniki część 2)
Zadania 2 (wyniki część 1)
Zadania 5 (wyniki)
Zadania 1 (wyniki)
Sygnaly i systemy 2FD Linia dluga, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
Zadania 2 (wyniki część 2)
Zadania 4 (wyniki część 1)
linia dluga
Linia dluga id 268593 Nieznany
cwiczenie 5 linia dluga id 1254 Nieznany
zadania z ćwiczeń, Statystyka - zadania, Wyniki badania dotyczącego liczby wyjazdów za granicę w cią
opracowanie A1 linia długa v2, WFiIS
Linia długa
Zadania 7 (wyniki)
Linia długa, ►Studia, Semestr 4, Elektrotechnika instrukcje
linia długa
więcej podobnych podstron