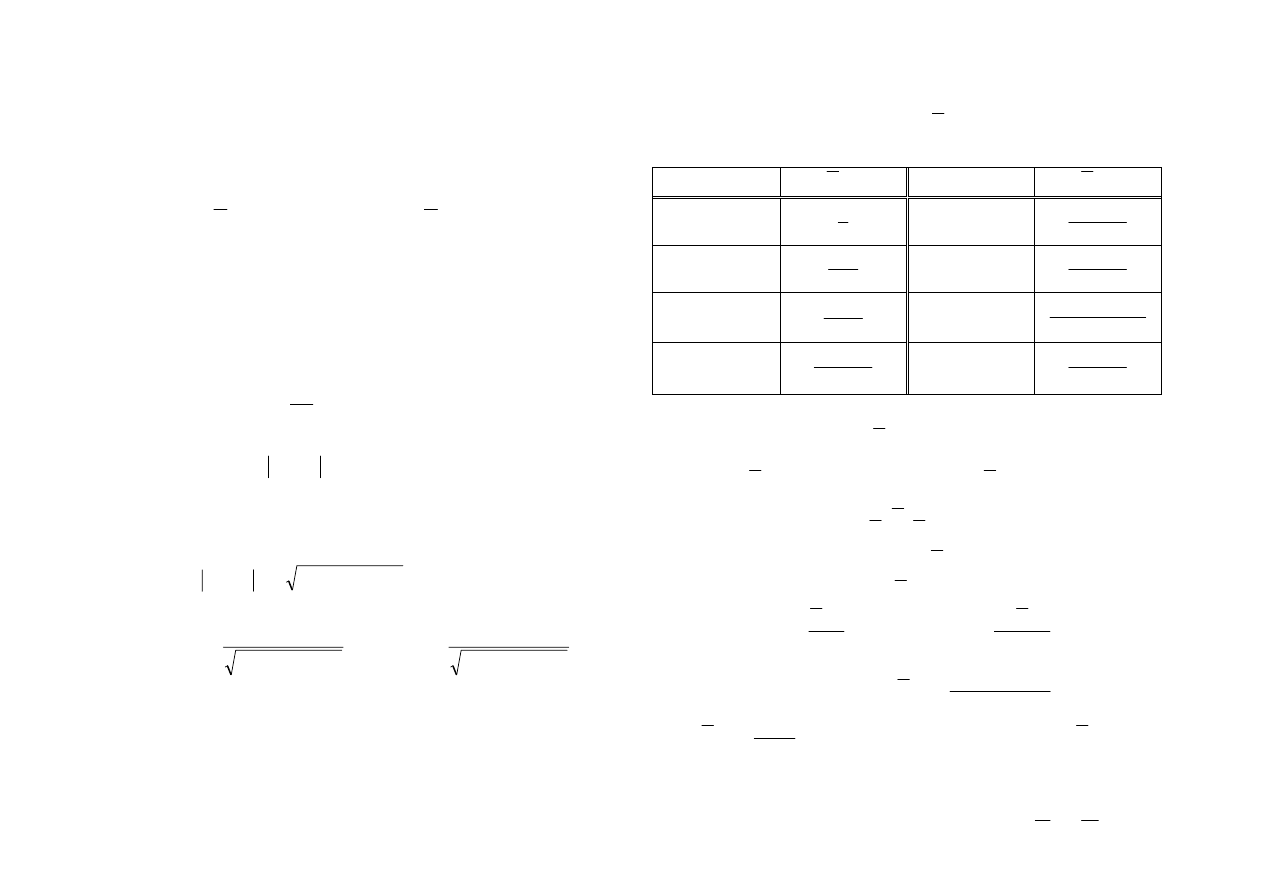
ZAKŁAD ANALIZY I TEORII OSOBLIWOŚCI
WZÓR CAŁKOWY FOURIERA
∫
+∞
+
=
0
]
sin
)
(
cos
)
(
[
)
(
ω
ω
ω
ω
ω
d
t
b
t
a
t
f
(CAŁKA FOURIERA)
∫
+∞
∞
−
=
τ
ωτ
τ
π
ω
d
f
a
cos
)
(
1
)
(
∫
+∞
∞
−
=
τ
ωτ
τ
π
ω
d
f
b
sin
)
(
1
)
(
PRZEKSZTAŁCENIE
F
F
∫
+∞
∞
−
−
=
dt
t
f
e
t
f
t
j
df
)
(
)]
(
[
ω
(
)
)
(
ω
j
F
ozn
=
F
1
−
∫
∞
∞
−
=
ω
ω
π
ω
ω
d
j
F
e
j
F
t
j
)
(
2
1
)]
(
[
(
)
)
(t
f
ozn
=
π
ω
θ
π
ω
ω
ω
θ
+
≤
≤
−
=
)
(
,
)
(
)
(
)
(
j
e
j
F
j
F
)]
(
)
(
[
)
(
ω
ω
π
ω
jb
a
j
F
−
=
WIDMO AMPLITUDOWE
)
(
)
(
)
(
2
2
ω
ω
π
ω
b
a
j
F
+
=
(
funkcja parzysta )
WIDMO FAZOWE
)
(
)
(
)
(
)
(
cos
2
2
ω
ω
ω
ω
θ
b
a
a
+
=
,
)
(
)
(
)
(
)
(
sin
2
2
ω
ω
ω
ω
θ
b
a
b
+
−
=
Jeżeli
1
)
(
cos
−
=
ω
θ
i
0
)
(
sin
=
ω
θ
, to
ω
π
ω
θ
sgn
)
(
=
dla
0
≠
ω
θ
- funkcja nieparzysta na
θ
D
lub
}
0
{
−
θ
D
PRZEKSZTAŁCENIE
L
L
(
)
∫
+∞ −
=
=
0
)
(
)
(
)]
(
[
s
f
dt
t
f
e
t
f
ozn
st
df
; f – oryginał
)
(t
f
)
(s
f
)
(t
f
)
(s
f
)
(t
1
s
1
R
∈
ω
ω
,
sin t
2
2
ω
ω
+
s
N
∈
n
t
n
,
1
!
+
n
s
n
R
∈
ω
ω
,
cos t
2
2
ω
+
s
s
C
∈
−
α
α
,
t
e
α
+
s
1
t
e
t
ω
α
sin
⋅
−
,
R
C
∈
∈
ω
α
,
2
2
)
(
ω
α
ω
+
+
s
R
∈
β
β
,
t
sh
2
2
β
β
−
s
R
∈
β
β
,
t
ch
2
2
β
−
s
s
L
)
0
(
)
(
)]
(
[
)
1
(
1
)
(
+
⋅
−
⋅
=
−
=
−
∑
k
n
k
k
n
n
n
f
s
s
f
s
t
f
L
)
0
(
)
(
)]
(
'
[
+
−
=
f
s
f
s
t
f
,
L
)
0
(
'
)
0
(
)
(
)]
(
''
[
2
+
−
+
−
=
f
sf
s
f
s
t
f
L
⋅
=
a
s
f
a
at
f
1
))
(
(
, gdy
0
>
a
L
0
),
(
)]
(
[
0
0
0
≥
⋅
=
−
−
t
s
f
e
t
t
f
st
L
[
]
)
(
)
(
α
α
+
=
⋅
−
s
f
t
f
e
t
,
C
∈
α
L
s
s
f
d
f
t
)
(
)
(
0
=
∫
τ
τ
,
L
N
∈
−
=
n
ds
s
f
d
t
f
t
n
n
n
n
,
)
(
)
1
(
)]
(
[
Dla oryginału okresowego f :
sT
T
st
e
dt
e
t
f
s
f
−
−
−
⋅
=
∫
1
)
(
)
(
0
(T – okres)
Dla
)
(
)
(
)
(
s
M
s
L
s
f
=
(funkcja wymierna) :
∑
⋅
=
i
st
s
e
s
f
res
t
f
i
]
)
(
[
)
(
SPLOT ORYGINAŁÓW:
)
(
)
(
)
(
2
1
t
f
t
f
t
F
∗
=
)
(
)
(
)
(
)
(
0
2
1
t
d
t
f
f
t
F
t
df
1
⋅
−
=
∫
τ
τ
τ
,
L
)
(
)
(
)]
(
[
2
1
s
f
s
f
t
F
⋅
=

PRZEKSZTAŁCENIE
Z
Z
(
)
)
(
)]
[(
0
z
X
z
x
x
ozn
n
n
n
df
n
=
=
∑
∞
=
;
,...)
,
(
)
(
1
0
x
x
x
n
=
n
x
)
(z
X
n
x
)
(z
X
1
1
−
z
z
C
∈
α
α
,
n
e
α
e
z
z
−
n
2
)
1
(
−
z
z
C
∈
ω
ω
,
sin n
1
cos
2
sin
2
+
−
ω
ω
z
z
z
2
n
3
)
1
(
)
1
(
−
+
z
z
z
C
∈
ω
ω
,
cos n
1
cos
2
)
cos
(
2
+
−
−
ω
ω
z
z
z
z
{ }
0
,
−
∈
C
a
a
n
a
z
z
−
!
1
n
z
e
1
Z
N
∈
⋅
=
−
−
k
z
X
z
x
k
k
n
,
)
(
)]
[(
Z
−
⋅
=
∑
−
=
+
1
0
)
(
)]
[(
k
k
k
n
z
x
z
X
z
x
ν
ν
ν
Z
dz
z
dX
z
nx
n
)
(
)]
[(
−
=
Dla
)
(
)
(
)
(
z
M
z
L
z
X
=
(funkcja wymierna) :
∑
−
⋅
=
i
n
z
n
z
z
X
res
x
i
]
)
(
[
1
SPLOT CIĄGÓW:
)
(
)
(
)
(
n
n
n
y
x
u
∗
=
,...
2
,
1
,
0
,
0
=
⋅
=
∑
=
−
n
y
x
u
n
n
n
ν
ν
ν
;
Z
)
(
)
(
)]
[(
z
Y
z
X
u
n
⋅
=
α
α
α
cos
sin
2
2
sin
=
α
α
α
α
2
2
2
2
sin
2
1
sin
cos
1
cos
2
2
cos
−
=
−
=
−
=
a
β
α
β
α
β
α
sin
cos
cos
sin
)
sin(
⋅
±
⋅
=
±
β
α
β
α
β
α
sin
sin
cos
cos
)
cos(
⋅
⋅
=
±
m
[
]
)
cos(
)
cos(
2
1
sin
sin
β
α
β
α
β
α
+
−
−
=
⋅
[
]
)
cos(
)
cos(
2
1
cos
cos
β
α
β
α
β
α
+
+
−
=
⋅
[
]
)
sin(
)
sin(
2
1
cos
sin
β
α
β
α
β
α
+
+
−
=
⋅
Wyszukiwarka
Podobne podstrony:
1 sciaga ppt
metro sciaga id 296943 Nieznany
ŚCIĄGA HYDROLOGIA
AM2(sciaga) kolos1 id 58845 Nieznany
Narodziny nowożytnego świata ściąga
finanse sciaga
Jak ściągać na maturze
Ściaga Jackowski
Aparatura sciaga mini
OKB SCIAGA id 334551 Nieznany
Przedstaw dylematy moralne władcy i władzy w literaturze wybranych epok Sciaga pl
fizyczna sciąga(1)
Finanse mala sciaga
Podział węży tłocznych ze względu na średnicę ściąga
OLIMPIADA BHP ŚCIĄGAWKA
Opracowanie Sciaga MC OMEN
więcej podobnych podstron