
EWSIE
Oleg Tikhonenko
SZKICE DO WYKŁADÓW
Z ANALIZY MATEMATYCZNEJ
Warszawa 2008

2
LITERATURA
1. Banach S. Rachunek różniczkowy i całkowy. T. 1, 2. PWN, Warszawa, 1957.
2. Żakowski W., Decewicz G. Matematyka. Cz. 1. WNT, Warszawa, 1994.
3. Krysicki W., Włodarski L. Analiza matematyczna w zadaniach. PWN, War-
szawa, 2001.
3
1. WSTĘP
Zbiory liczbowe. Przedziały. Kresy
Będziemy nadal stosować następujące oznaczenia
...}
,
2
,
1
{
:
=
N
– zbiór liczb naturalnych (Uwaga: U nas
N
∉
0
),
}
0
{
...}
,
2
,
1
,
0
{
:
0
U
N
N
=
=
– zbiór liczb całkowitych nieujemnych,
...}
,
2
,
1
,
0
{
:
±
±
=
Z
– zbiór liczb całkowitych,
∈
∈
=
N
Z
Q
q
p
q
p
,
:
:
– zbiór liczb wymiernych,
R –
zbiór liczb rzeczywistych.
Oczywiście
R
Q
Z
N
N
⊂
⊂
⊂
⊂
0
.
Oznaczenia przedziałów w R:
)
;
(
b
a
– przedział otwarty (zbiór takich
R
∈
x
, że
)
b
x
a
<
<
,
]
;
[
b
a
– przedział domknięty (zbiór takich
R
∈
x
, że
)
b
x
a
≤
≤
,
]
;
(
b
a
– przedział lewostronnie otwarty albo prawostronnie domknięty (zbiór ta-
kich
R
∈
x
, że
)
b
x
a
≤
<
,
)
;
[
b
a
– przedział prawostronnie otwarty albo lewostronnie domknięty (zbiór ta-
kich
R
∈
x
, że
)
b
x
a
<
≤
.
Dowolny przedział w R będziemy zwykle oznaczać przez
∆
.
Mówimy, że zbiór
R
∈
A
jest ograniczony z góry, jeżeli
C
x
A
x
C
≤
∀
∃
∈
∈
:
:
R
.
Najmniejszą liczbę C o tej własności nazywamy supremum (kresem górnym) zbioru
A
i oznaczamy sup A. Np. jeżeli
)
2
;
1
(
=
A
, to
2
sup
=
A
(zauważmy, że w tym
przypadku
A
A∉
sup
).
Jeżeli zbiór
R
∈
A
nie jest ograniczony z góry, to przyjmujemy
+∞
=
A
sup
.
Podobnie, mówimy, że zbiór
R
∈
A
jest ograniczony z dołu, jeżeli
C
x
A
x
C
≥
∀
∃
∈
∈
:
:
R
.
Największą liczbę C o tej własności nazywamy infimum (kresem dolnym) zbioru A i
oznaczamy inf A.
Jeżeli zbiór
R
∈
A
nie jest ograniczony z dołu, to przyjmujemy
−∞
=
A
inf
.
Iloczyn kartezjański dwóch zbiorów:
}.
,
:
)
,
{(
:
B
y
A
x
y
x
B
A
∈
∈
=
×
Jeżeli
B
A
=
, to zamiast
A
A
×
piszemy często
2
A
.

4
Iloczyn kartezjański skończonej liczby zbiorów:
}
...,
,
:
)
...,
,
{(
:
...
1
1
1
1
n
n
n
n
A
x
A
x
x
x
A
A
∈
∈
=
×
×
;
n
A
A
A
=
×
×
:
...
.
Zasada indukcji matematycznej
Przypuśćmy, że mamy ciąg twierdzeń
N
∈
n
n
T
),
(
. .asada indukcji matema-
tycznej mówi, że aby udowodnić ten ciąg twierdzeń wystarczy udowodnić
)
1
(
T
oraz
sprawdzić, iż dla dowolnego
k
n
= z prawdziwości twierdzenia
)
(k
T
(założenia in-
dukcyjnego) wynika prawdziwość twierdzenia
)
1
(
+
k
T
. Tę drugą część nazywamy
krokiem indukcyjnym
.
Nierówność Bernoulliego
nx
x
n
+
≥
+
1
)
1
(
,
,
1
−
>
x
N
∈
n
.
Istotnie, dla
1
=
n
nierówność jest oczywista:
x
x
⋅
+
≥
+
1
1
)
1
(
1
. Przypuśćmy, że
nierówność zachodzi dla pewnego
k
n
= . Pokażemy, że jest ona prawdziwa dla
1
+
= k
n
. Liczymy: według założenia indukcji mamy
=
+
+
≥
+
⋅
+
=
+
+
)
1
)(
1
(
)
1
(
)
1
(
)
1
(
1
x
kx
x
x
x
k
k
x
k
kx
x
kx
)
1
(
1
1
2
+
+
≥
+
+
+
=
.
Silnia:
)
1
(
!
)!
1
(
,
1
:
!
0
+
⋅
=
+
=
n
n
n
.
Symbol dwumienny Newtona:
!
)
1
)...(
1
(
)
!
(
!
!
:
k
k
n
n
n
k
n
k
n
k
n
+
−
−
=
−
=
,
n
k
,
0
=
.
Liczba
k
n
określa liczbę kombinacji k-elementowych ze zbioru n-elementowego,
czyli liczbę różnych k-elementowych podzbiorów zbioru n-elementowego. .auważ-
my, że
−
=
k
n
n
k
n
,
n
k
,
0
=
.
Odnotujmy, że
1
0
=
=
n
n
n
,
n
n
n
n
=
−
=
1
1
,
2
)
1
(
2
2
−
=
−
=
n
n
n
n
n
.
n razy

5
Wzór dwumienny Newtona
∑
=
−
=
+
n
i
i
i
n
n
b
a
i
n
b
a
0
)
(
.
Dowód indukcyjny. Dla
1
=
n
wzór jest oczywisty:
1
1
1
0
0
1
1
1
1
0
1
)
(
b
a
b
a
b
a
b
a
−
−
+
=
+
=
+
.
Przypuśćmy, że wzór zachodzi dla
k
n
= :
∑
=
−
=
+
k
i
i
i
k
k
b
a
i
k
b
a
0
)
(
. Sprawdźmy
go dla
1
+
= k
n
:
=
+
=
+
⋅
+
=
+
∑
=
−
+
)
(
)
(
)
(
)
(
0
1
b
a
b
a
i
k
b
a
b
a
b
a
k
i
i
i
k
k
k
=
−
+
=
+
=
∑
∑
∑
∑
=
+
=
−
+
−
+
=
=
+
−
+
−
k
i
k
i
i
i
k
i
i
k
k
i
k
i
i
i
k
i
i
k
b
a
i
k
b
a
i
k
b
a
i
k
b
a
i
k
0
1
1
1
1
0
0
1
1
1
=
+
−
+
+
=
+
−
+
=
+
∑
1
0
1
1
0
1
1
k
i
i
k
k
i
k
b
a
b
a
i
k
i
k
b
a
∑
∑
+
=
−
+
+
−
+
=
+
+
=
+
+
+
+
+
+
=
1
0
1
1
0
1
1
0
1
1
1
1
1
0
1
k
i
i
i
k
k
i
i
k
k
i
k
b
a
i
k
b
a
k
k
b
a
i
k
b
a
k
,
ponieważ
=
+
−
+
−
−
=
+
−
−
+
−
=
−
+
1
1
1
)!
(
)!
1
(
!
)!
1
(
)!
1
(
!
)!
(
!
!
1
i
k
i
i
k
i
k
i
k
i
k
i
k
i
k
i
k
i
k
+
=
−
+
+
=
+
−
+
⋅
−
−
=
i
k
i
k
i
k
i
k
i
k
i
k
i
k
1
)!
1
(
!
)!
1
(
)
1
(
1
)!
(
)!
1
(
!
,
n
k
,
1
=
.
Funkcje
Jeżeli
X
i Y są pewnymi zbiorami, to funkcją (odwzorowaniem X w Y)
Y
X
f
→
:
nazywamy dowolne przyporządkowanie każdemu elementowi
X
x
∈ dokładnie jedne-
go elementu
Y
y
∈ .
Jeżeli określona jest funkcja
Y
X
f
→
:
, to piszemy
)
(x
f
y
=
, co oznacza, że w
punkcie x funkcja przyjmuje wartość
)
(x
f
. Będziemy nadal zakładać, że
R
⊂
X
,
R
⊂
Y
(rys.1). W zapisie
)
(x
f
y
=
symbol x nazywa się argumentem funkcji
)
(x
f
.
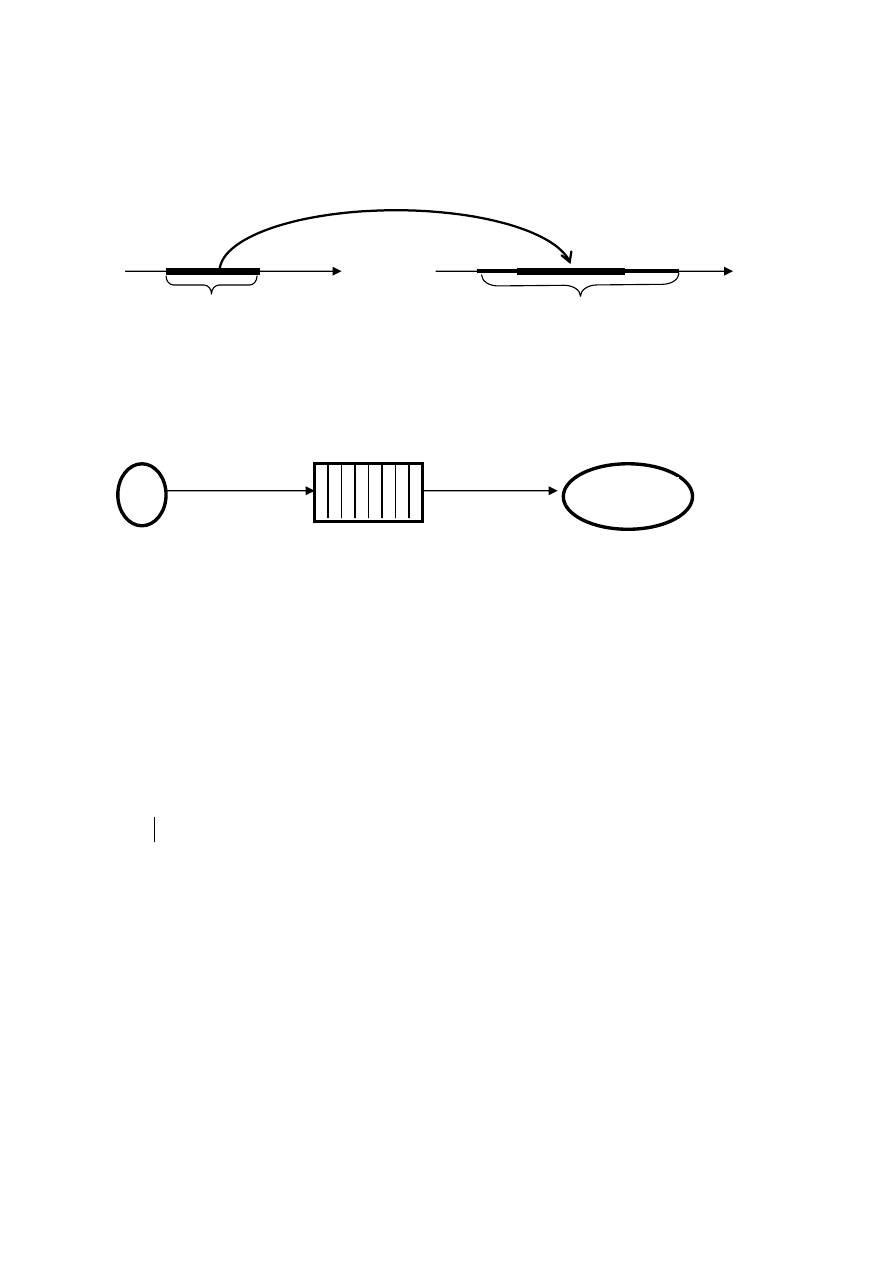
6
Rys. 1
Funkcję można sobie wyobrazić jako „czarną skrzynkę”, która przetwarza we-
dług ustalonej reguły liczby z jednego zbioru na liczby z drugiego zbioru (rys. 2).
Rys. 2
.biór X nazywa się dziedziną funkcji
Y
X
f
→
:
(oznaczamy go także
f
D
), a
zbiór Y nazywa się jej przeciwdziedziną. .biór
}
:
)
(
{
f
D
x
Y
x
f
∈
∈
nazywamy zbio-
rem wartości funkcji f i oznaczamy przez
f
W
.
Jeżeli dany jest tylko wzór określający funkcję, to zbiór tych elementów z R, dla
których wzór ten ma sens, nazywamy dziedziną naturalną funkcji.
Zbiór
)}
(
:
)
,
{(
x
f
y
Y
X
y
x
=
×
∈
nazywamy wykresem odwzorowania (funkcji) f.
Jeżeli
Y
X
f
→
:
i
X
A
⊂
, to funkcję f, ograniczoną do zbioru A oznaczamy
przez
Y
A
f
A
→
:
i nazywamy zaciśnieniem (restrykcją) funkcji f do A. Jeżeli
X
A
⊂
, to zbiór
}
:
)
(
{
:
)}
(
{
A
x
x
f
A
f
∈
=
nazywamy obrazem zbioru A.
Odwzorowanie (funkcję)
Y
X
f
→
:
(
)
(x
f
y
=
) nazywamy injektywnym albo
różnowartościowym (injektywną albo różnowartościową)
, jeżeli
)
(
)
(
b
f
a
f
≠
, dla
dowolnych
X
b
a
∈
,
,
b
a
≠ . Dla przykładu, odwzorowanie (funkcja)
]
1
;
1
[
:
sin
−
→
R
(
x
y
sin
=
) nie jest injektywne (injektywna).
Odwzorowanie (funkcję)
Y
X
f
→
:
(
)
(x
f
y
=
) nazywamy surjektywnym (sur-
jektywną)
, jeżeli
Y
X
f
=
)
(
, tj. zbiór Y jest obrazem zbioru X (
f
W
Y
=
). Dla przykła-
du, odwzorowanie (funkcja)
]
1
;
1
[
:
sin
−
→
R
(
x
y
sin
=
) jest surjektywne (surjektyw-
na).
Odwzorowanie (funkcję)
Y
X
f
→
:
(
)
(x
f
y
=
)
, które (która) jest jednocześnie
injektywne i surjektywne (injektywna i surjektywna), nazywamy bijektywnym albo
R
X
R
Y
)
(x
f
y
=
x
)
(x
f
y
=
)
(x
f
7
odwzorowaniem X na Y (bijektywną)
. Jeżeli f jest bijektywna, to możemy określić
odwzorowanie (funkcję) odwrotne Y na X (odwrotną)
X
Y
f
→
−
:
1
,
y
x
f
x
y
f
=
⇔
=
−
)
(
:
)
(
1
.
Funkcja injektywna nazywa się czasami wzajemnie jednoznaczną odpowiedniością.
Dla przykładu, odwzorowanie
2
:
)
(
),
;
0
[
)
;
0
[
:
x
x
f
f
=
∞
+
→
∞
+
jest bijektywne
i
y
y
f
=
−
)
(
1
.
Jeżeli
R
∈
Y
X
,
i
)
(x
f
y
=
jest funkcją bijektywną, to wykres funkcji
)
(
1
y
f
−
jest symetryczny do wykresu funkcji
)
(x
f
względem prostej
x
y =
.
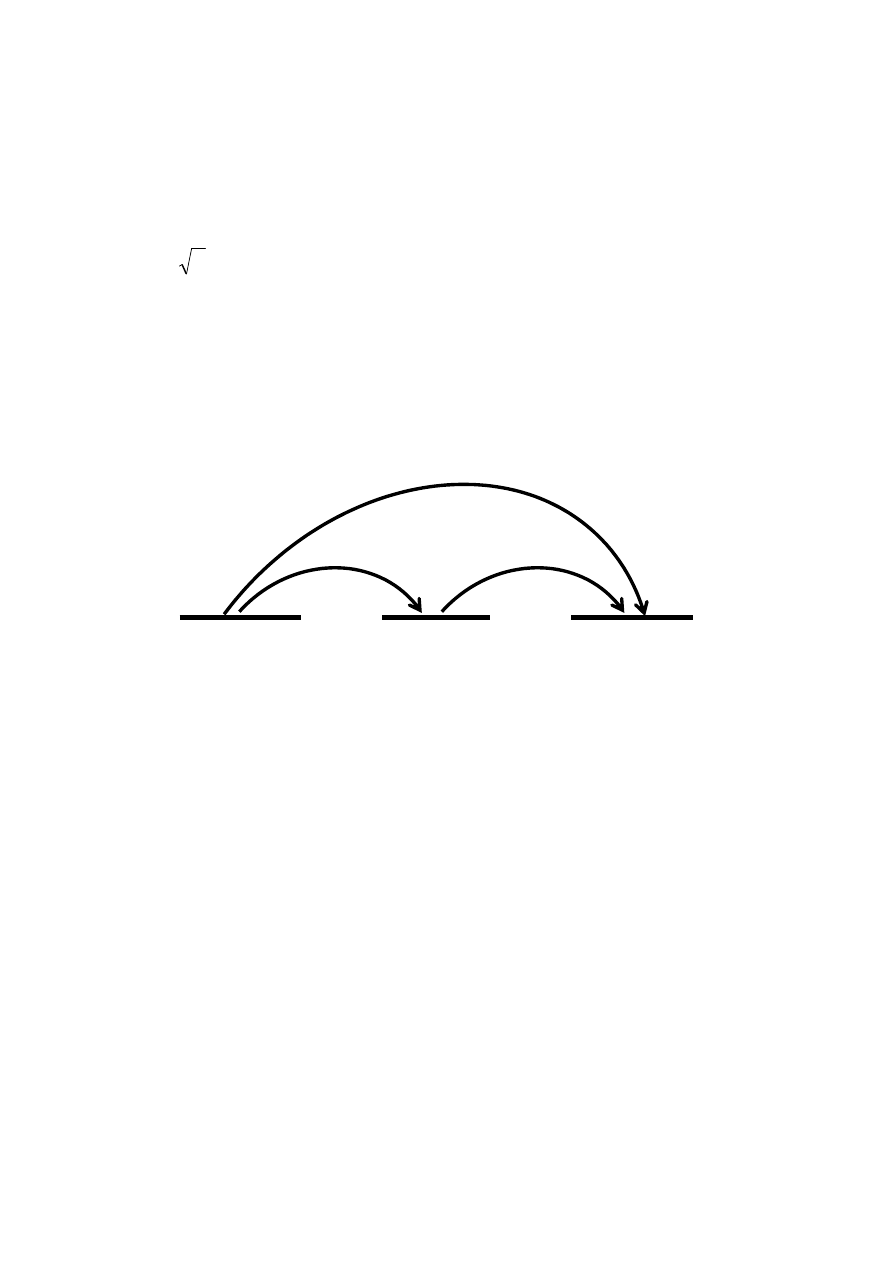
Odwzorowania można składać (rys. 3): jeżeli
Y
X
f
→
:
i
Z
Y
g
→
:
, to
Z
X
f
g
→
:
o
,
))
(
(
:
)
)(
(
x
f
g
x
f
g
=
o
,
X
x ∈
.
Symbol
f
g o czytamy f złożone z g lub g nałożone na f.
Rys. 3
Odnotujmy, że jeżeli
Y
Z
=
, to na ogół
g
f
f
g
o
o
≠
, np.
)
sin(
)
(sin
2
2
x
x
≠
.
Składanie odwzorowań jest łączne, tzn.
f
g
h
f
g
h
o
o
o
o
)
(
)
(
=
.
Niech
R
⊂
X
będzie zbiorem takim, że
X
x
X
x
∈
−
⇒
∈
, np.
)
1
;
1
(−
=
X
. Niech
R
→
X
f
:
. Mówimy, że funkcja f jest parzysta, jeżeli
)
(
)
(
x
f
x
f
=
−
dla dowolnego
X
x ∈
. Dla przykładu funkcje:
)
(
)
;
0
[
:
,
:
)
(
2
N
R
∈
∞
+
→
=
k
f
x
x
f
k
,
)
(
)
;
0
[
}
0
{
\
:
,
:
)
(
2
N
R
∈
∞
+
→
=
−
k
f
x
x
f
k
,
]
1
;
1
[
:
cos
−
→
R
są parzyste.
Funkcje parzyste nie są injektywne (z wyjątkiem przypadku zdegenerowanego,
gdy
}
0
{
=
X
).
Jeżeli
)
(
)
(
x
f
x
f
−
=
−
dla dowolnego
X
x ∈
, to mówimy, że funkcja f jest niepa-
rzysta.
Dla przykładu funkcje:
)
(
:
,
:
)
(
1
2
N
R
R
∈
→
=
+
k
f
x
x
f
k
,
)
(
}
0
{
\
:
,
:
)
(
1
2
N
R
R
∈
→
=
+
−
k
f
x
x
f
k
,
X
Y
Z
f
g
g
f o

8
]
1
;
1
[
:
sin
−
→
R
,
R
Z
R
→
∈
π
+
π
k
k
:
2
\
:
tg
,
R
Z
R
→
∈
π
}
:
{
\
:
ctg
k
k
są nieparzyste.
Niech
R
⊂
X
będzie zbiorem takim, że istnieje liczba
0
>
ω
taka, że
X
x
X
x
∈
ω
+
⇒
∈
. Niech
R
→
X
f
:
.
Mówimy, że funkcja f jest okresowa o okre-
sie ω
, jeżeli
)
(
)
(
x
f
x
f
=
ω
+
dla dowolnego
X
x ∈
. Najmniejszą liczbę
0
>
ω
o po-
wyższych własnościach nazywamy okresem podstawowym funkcji f. Funkcje okre-
sowe nie są injektywne.
Funkcje trygonometryczne są okresowe:
]
1
;
1
[
:
sin
−
→
R
,
]
1
;
1
[
:
cos
−
→
R
mają okres podstawowy
π
=
ω 2 ;
R
Z
R
→
∈
π
+
π
k
k
:
2
\
:
tg
,
R
Z
R
→
∈
π
}
:
{
\
:
ctg
k
k
mają okres podstawowy
π
=
ω
.
Mówimy, że funkcja f jest ograniczona z góry, gdy jest ograniczony z góry zbiór
jej wartości
f
W
, tzn.
C
x
f
X
x
C
≤
∀
∃
∈
∈
)
(
:
:
R
.
Analogicznie, funkcja f jest ograniczona z dołu, gdy jest ograniczony z dołu
zbiór jej wartości
f
W
, tzn.
C
x
f
X
x
C
≥
∀
∃
∈
∈
)
(
:
:
R
.
Niech
R
⊂
X
i niech
R
→
X
f
:
.
Mówimy, że f jest rosnąca (słabo rosnąca,
niemalejąca)
, jeżeli dla dowolnych
X
x
x
∈
2
1
,
takich, że
2
1
x
x
< mamy
)
(
)
(
2
1
x
f
x
f
≤
.
Jeżeli dla dowolnych
X
x
x
∈
2
1
,
takich, że
2
1
x
x
< mamy
)
(
)
(
2
1
x
f
x
f
<
, to mó-
wimy, że f jest ściśle (silnie) rosnąca.
Przy zmianie zwrotu nierówności otrzymujemy funkcje malejące (słabo maleją-
ce, nierosnące)
i ściśle (silnie) malejące. Funkcje malejące i rosnące nazywamy
funkcjami monotonicznymi. Funkcje ściśle malejące i ściśle rosnące nazywamy funk-
cjami ściśle monotonicznymi. Każda funkcja ściśle monotoniczna jest oczywiście in-
jektywna.
Np. funkcja
)
(
:
,
:
)
(
1
2
N
R
R
∈
→
=
+
k
f
x
x
f
k
jest ściśle rosnąca.
Uwaga: Funkcja
x
y
1
= jest monotoniczna w każdym z przedziałów
)
0
;
(
−∞
i
)
,
0
(
∞
+
, ale nie jest monotoniczna w całej swojej dziedzinie
)
;
0
(
)
0
;
(
∞
+
−∞
U
.
9
Niech
R
⊂
∆′
∆,
będą dowolnymi przedziałami,
∆′
→
∆
:
f
. Wówczas f jest
biektywna wtedy i tylko wtedy, gdy jest ściśle monotoniczna. Ponadto, funkcja od-
wrotna
1
−
f
ma tę samą monotoniczność co f.
Funkcje elementarne
Podstawowymi funkcjami elementarnymi nazywamy funkcje: stałe, potęgowe,
wykładnicze, logarytmiczne, trygonometryczne oraz cyklometryczne (odwrotne try-
gonometryczne). Funkcje, które można otrzymać z podstawowych funkcji elementar-
nych za pomocą skończonej liczby działań arytmetycznych oraz operacji złożenia
funkcji, nazywamy funkcjami elementarnymi.
Funkcje potęgowe i pierwiastkowe:
k
x
x
f
=
:
)
(
,
R
R →
:
f
, gdzie
N
∈
k
. Gdy k
jest liczbą nieparzystą, to funkcja
k
x jako odwzorowanie
R
R →
jest bijektywna.
Funkcja do niej odwrotna to pierwiastek stopnia (nieparzystego) k (jest on okre-
ślony dla wszystkich
R
∈
x
).
Jeżeli k jest liczbą parzystą, to funkcja
k
x jako odwzorowanie
R
R →
nie jest
injektywna.
Jeżeli ograniczymy się do przedziału
)
;
0
[
∞ , to staje się ona bijekcją
)
;
0
[
∞
+
→
)
;
0
[
∞
+
. Funkcja do niej odwrotna to pierwiastek stopnia parzystego (jest on okre-
ślony tylko dla
0
≥
x
).
Wielomiany:
0
1
1
1
...
)
(
a
x
a
x
a
x
a
x
p
n
n
n
n
+
+
+
+
=
−
−
,
gdzie
0
N
∈
n
,
R
∈
0
...,
,
a
a
n
. Jeżeli
0
≠
n
a
, to mówimy, że p jest wielomianem stopnia n i piszemy
n
p
=
deg
.
Funkcje wymierne:
)
(
)
(
)
(
x
q
x
p
x
r
=
, gdzie p, q są wielomianami; funkcja r jest
określona na zbiorze
}
0
)
(
:
{
\
=
∈
x
q
x
R
R
. Np. funkcja
k
x
x
r
1
:
)
(
=
jest określona dla
0
≠
x
(
*
R
∈
x
, gdzie
}
0
{
\
*
R
R
=
).
Podstawowe wzory:
k
k
x
x
1
=
−
(
*
R
∈
x
,
Z
∈
k
),
l
k
l
k
x
x
x
⋅
=
+
(
*
R
∈
x
,
Z
∈
l
k
,
),
l
k
l
k
x
x
x
=
−
(
*
R
∈
x
,
Z
∈
l
k
,
),
l
k
l
k
x
x
⋅
=
)
(
(
*
R
∈
x
,
Z
∈
l
k
,
).

10
Jeżeli
0
>
x
, to powyższe wzory są prawdziwe dla dowolnych
Q
∈
l
k
,
. Uwaga:
Jeżeli
0
<
x
, to np. ostatni wzór nie jest prawdziwy dla dowolnych
Q
∈
l
k
,
. Dla
przykładu:
( )
1
1
)
1
(
)
1
(
)
1
(
1
2
1
2
1
2
2
2
1
=
=
−
≠
−
=
−
=
−
.
Funkcje wykładnicze i logarytmiczne:
x
a
x
f
=
:
)
(
,
)
;
0
(
:
∞
+
→
R
f
, gdzie
0
>
a
,
1
≠
a
. Jeżeli
1
>
a
, to funkcja wykładnicza jest ściśle rosnąca i jest bijekcją
)
;
0
(
∞
+
→
R
.
Jeżeli
1
0
<
< a
, to funkcja wykładnicza jest ściśle malejąca i również jest bijek-
cją
)
;
0
(
∞
+
→
R
. Funkcja odwrotna to
R
→
∞
+ )
;
0
(
:
log
a
,
x
a
x
a
=
log
,
0
>
x
,
x
a
x
a
=
log
,
R
∈
x
.
Podstawowe wzory:
1
0
=
a
,
a
a
=
1
(
0
>
a
),
q
p
q
p
a
a
a
⋅
=
+
(
0
>
a
,
R
∈
q
p,
),
q
p
q
p
a
a
⋅
=
)
(
(
0
>
a
,
R
∈
q
p,
),
0
1
log
=
a
,
1
log
=
a
a
(
0
>
a
,
1
≠
a
),
q
p
q
p
a
a
a
log
log
)
(
log
+
=
⋅
(
0
>
a
,
1
≠
a
,
0
,
>
q
p
),
q
p
q
p
a
a
a
log
log
log
−
=
(
0
>
a
,
1
≠
a
,
0
,
>
q
p
),
p
q
p
a
q
a
log
)
(
log
⋅
=
(
0
>
a
,
1
≠
a
,
0
>
p
,
R
∈
q
).
Funkcje trygonometryczne i funkcje do nich odwrotne:
Funkcje trygonometrycz-
ne sin, cos, tg i ctg, jako funkcje okresowe, nie są oczywiście injektywne.
Podstawowe wzory:
x
x
sin
)
sin(
−
=
−
,
x
x
cos
)
cos(
=
−
,
x
x
tg
)
(
tg
−
=
−
,
x
x
ctg
)
(
ctg
−
=
−
,
1
cos
sin
2
2
=
+
x
x
,
x
x
2
2
cos
1
tg
1
=
+
,
y
x
y
x
y
x
sin
cos
cos
sin
)
sin(
⋅
+
⋅
=
+
,
x
x
x
cos
sin
2
2
sin
=
,
y
x
y
x
y
x
sin
sin
cos
cos
)
cos(
⋅
−
⋅
=
+
,
x
x
x
2
2
sin
cos
2
cos
−
=
,
y
x
y
x
y
x
tg
tg
1
tg
tg
)
(
tg
⋅
−
+
=
+
,

11
y
x
y
x
y
x
ctg
ctg
1
ctg
ctg
)
(
ctg
+
−
⋅
=
+
,
x
x
x
2
tg
1
tg
2
2
tg
−
=
,
x
x
x
ctg
2
1
ctg
2
ctg
2
−
=
,
2
cos
2
sin
2
sin
sin
y
x
y
x
y
x
−
+
=
+
,
2
sin
2
cos
2
sin
sin
y
x
y
x
y
x
−
+
=
−
,
2
cos
2
cos
2
cos
cos
y
x
y
x
y
x
−
+
=
+
,
2
sin
2
sin
2
cos
cos
y
x
y
x
y
x
−
+
−
=
−
,
π
+
β
=
α
⇔
β
=
α
n
2
sin
sin
lub
π
+
β
−
π
=
α
n
2
(
Z
∈
n
),
π
+
β
=
α
⇔
β
=
α
n
2
cos
cos
lub
π
+
β
−
=
α
n
2
(
Z
∈
n
),
Wzory redukcyjne:
x
x
cos
)
2
sin(
=
π
+
,
x
x
sin
)
2
cos(
−
=
π
+
,
x
x
ctg
)
2
(
tg
−
=
π
+
,
x
x
tg
)
2
(
ctg
−
=
π
+
,
x
x
sin
)
sin(
−
=
π
+
,
x
x
cos
)
cos(
−
=
π
+
,
x
x
tg
)
(
tg
=
π
+
,
x
x
ctg
)
(
ctg
=
π
+
,
x
x
cos
)
2
3
sin(
−
=
π
+
,
x
x
sin
)
2
3
cos(
=
π
+
,
x
x
ctg
)
2
3
(
tg
−
=
π
+
,
x
x
tg
)
2
3
(
ctg
−
=
π
+
.
Funkcje trygonometryczne sin, cos, tg i ctg możemy zacieśnić, tak by stały się
bijektywne:
" sin:
]
1
;
1
[
2
;
2
−
→
π
π
−
;
funkcja odwrotna to arc sin:
π
π
−
→
−
2
;
2
]
1
;
1
[
.
x
x
=
)
sin(arcsin
dla
]
1
;
1
[
−
∈
x
,
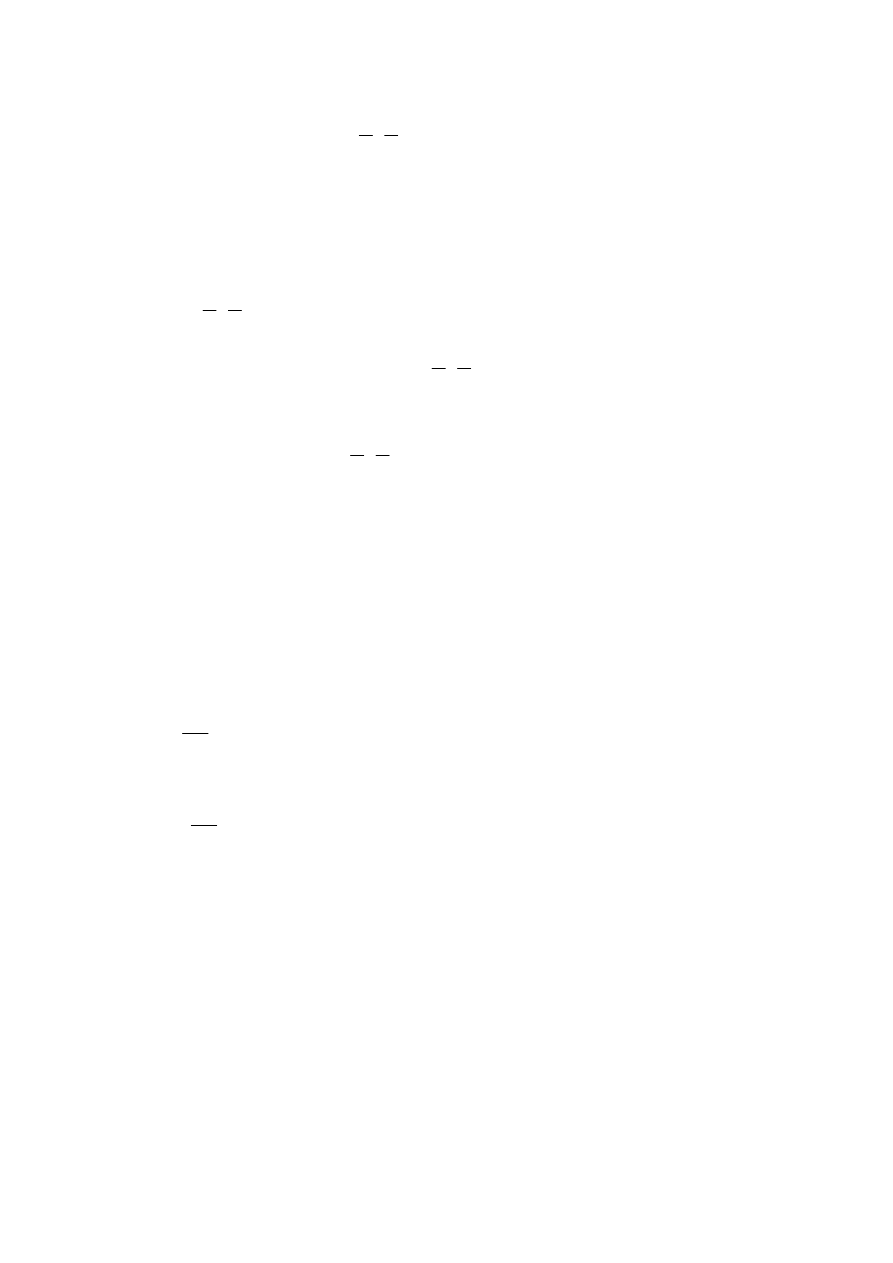
12
x
x
=
)
arcsin(sin
dla
π
π
−
∈
2
;
2
x
.
icos:
]
1
;
1
[
]
;
0
[
−
→
π
;
funkcja odwrotna to arc cos:
]
;
0
[
]
1
;
1
[
π
→
−
.
x
x
=
)
cos(arccos
dla
]
1
;
1
[
−
∈
x
,
x
x
=
)
arccos(cos
dla
[ ]
π
∈ ;
0
x
.
itg:
R
→
π
π
−
2
;
2
;
funkcja odwrotna to arc tg:
π
π
−
→
2
;
2
R
.
x
x
=
)
tg
(arc
tg
dla
R
∈
x
,
x
x
=
)
(tg
tg
arc
dla
π
π
−
∈
2
;
2
x
.
ictg:
R
→
π)
;
0
(
;
funkcja odwrotna to arc ctg:
)
;
0
(
π
→
R
.
x
x
=
)
ctg
(arc
ctg
dla
R
∈
x
,
x
x
=
)
(ctg
ctg
arc
dla
)
;
0
(
π
∈
x
.
Funkcja
α
x : Jest to funkcja
)
;
0
(
)
;
0
(
∞
+
→
∞
+
określona wzorem
α
= x
x
f
:
)
(
,
gdzie
R
∈
α
.
Podstawowe wzory:
α
α
−
=
x
x
1
(
R
∈
α
> ,
0
x
),
β
α
β
+
α
⋅
=
x
x
x
(
R
∈
β
α
>
,
,
0
x
),
β
α
β
−
α
=
x
x
x
(
R
∈
β
α
>
,
,
0
x
),
β
⋅
α
β
α
= x
x )
(
(
R
∈
β
α
>
,
,
0
x
).
13
Wykresy podstawowych funkcji elementarnych
x
y
cos
=
x
y
sin
=
2
x
y
=
-1,5
-1
-0,5
0
0,5
1
1,5
-15
-12,5
-10
-7,5
-5
-2,5
0
2,5
5
7,5
10
12,5
15
-1,5
-1
-0,5
0
0,5
1
1,5
-15
-12,5
-10
-7,5
-5
-2,5
0
2,5
5
7,5
10
12,5
15
0
1
2
3
4
5
-3
-2
-1
0
1
2
3
14
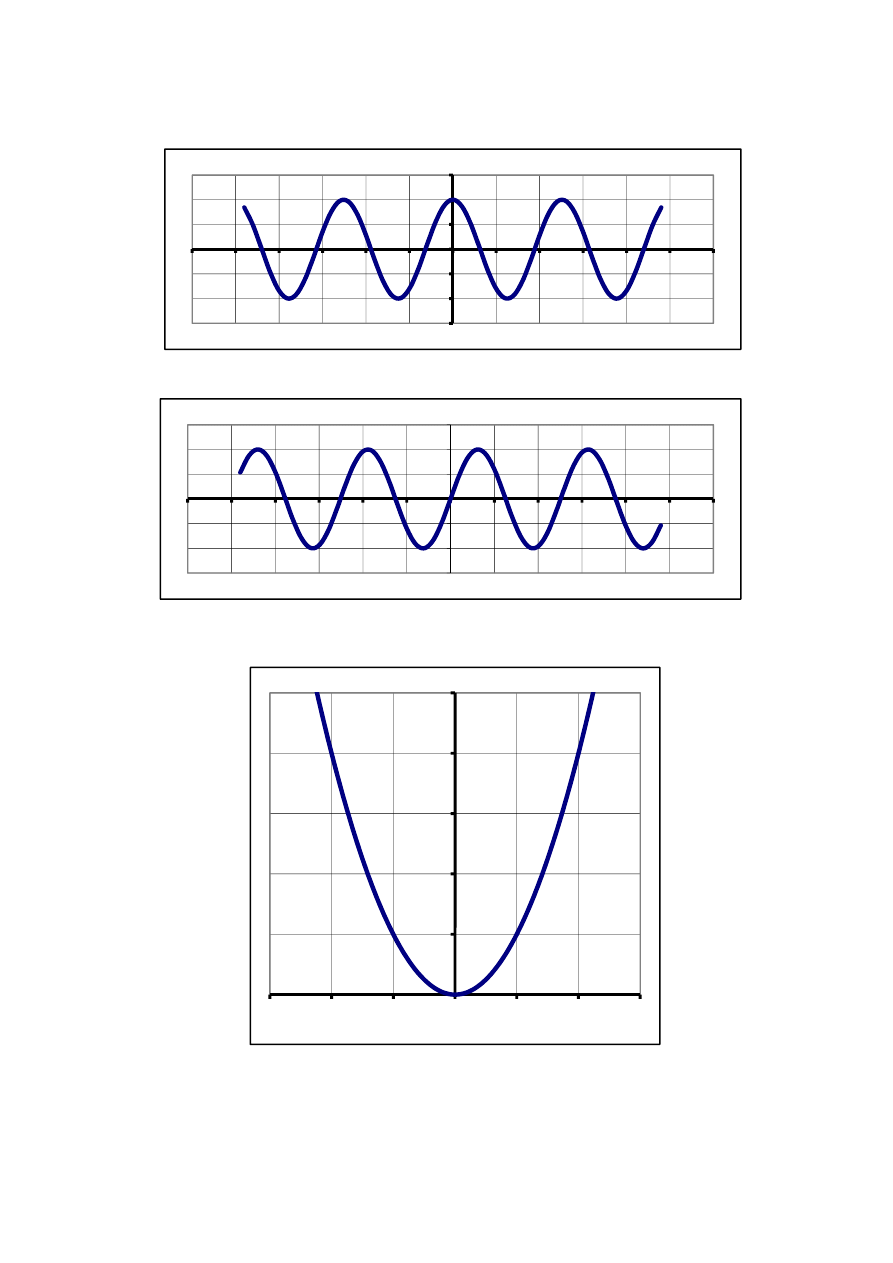
3
x
y
=
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
-3
-2
-1
0
1
2
3
15
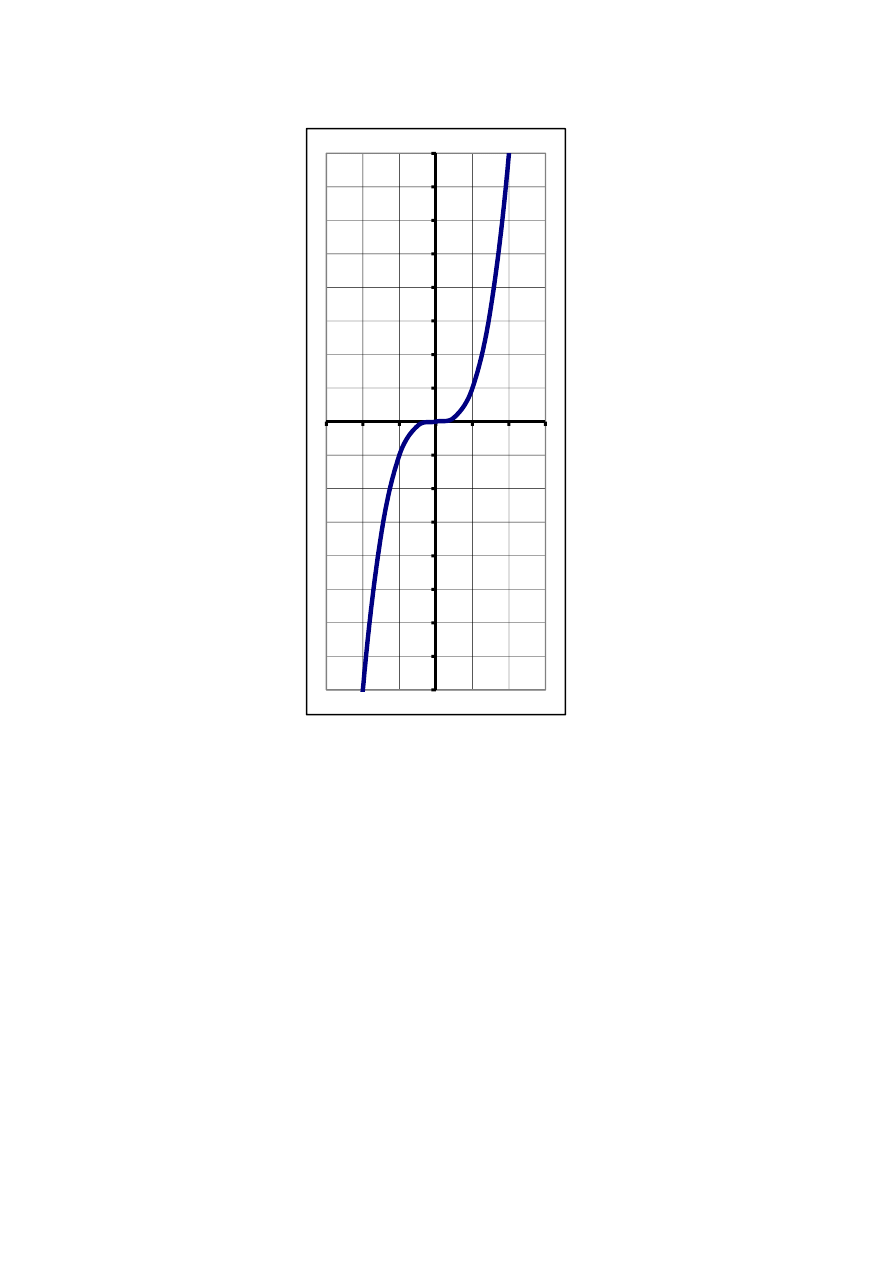
x
y
2
=
i
x
y
2
log
=
x
y
=
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
-10 -9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
0
1
2
3
4
5
6
7
8
9
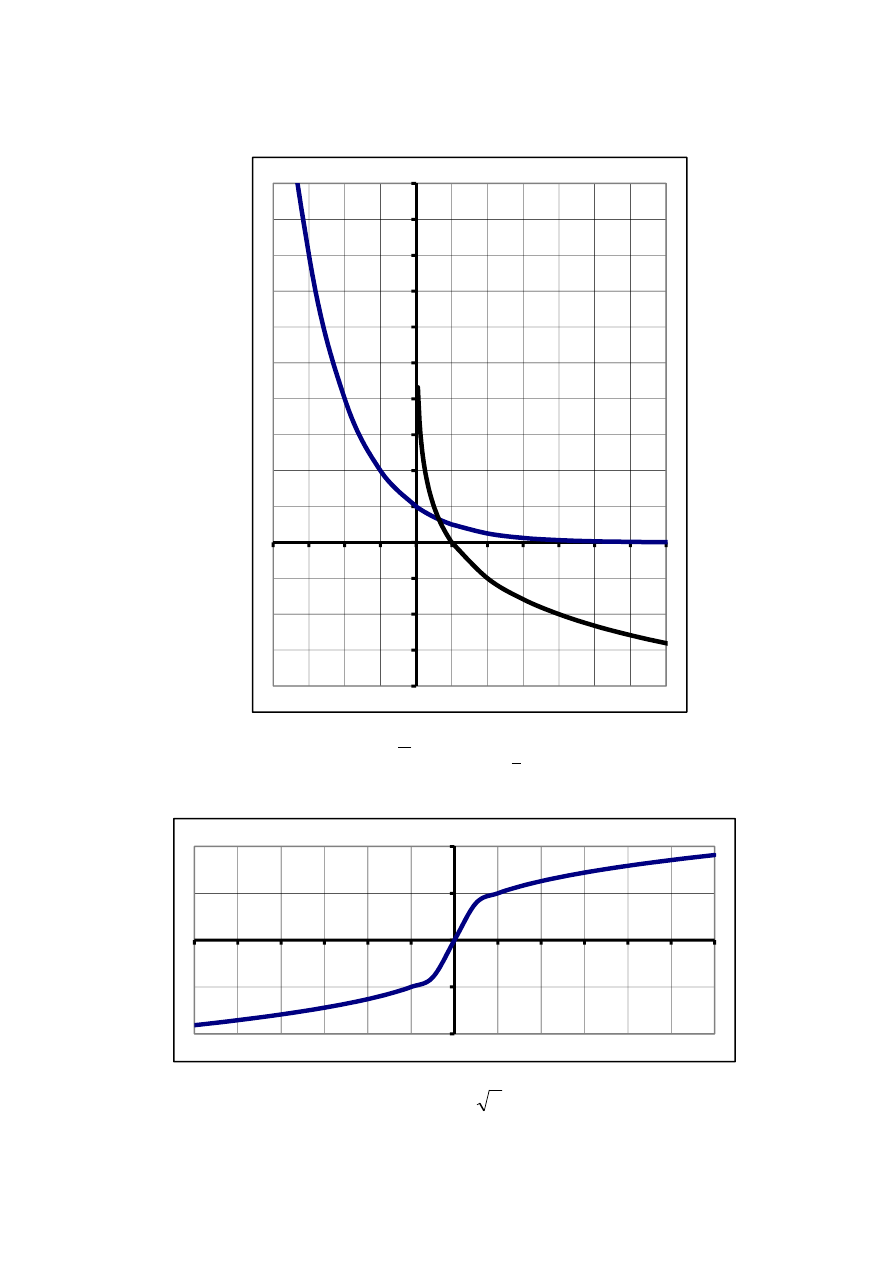
16
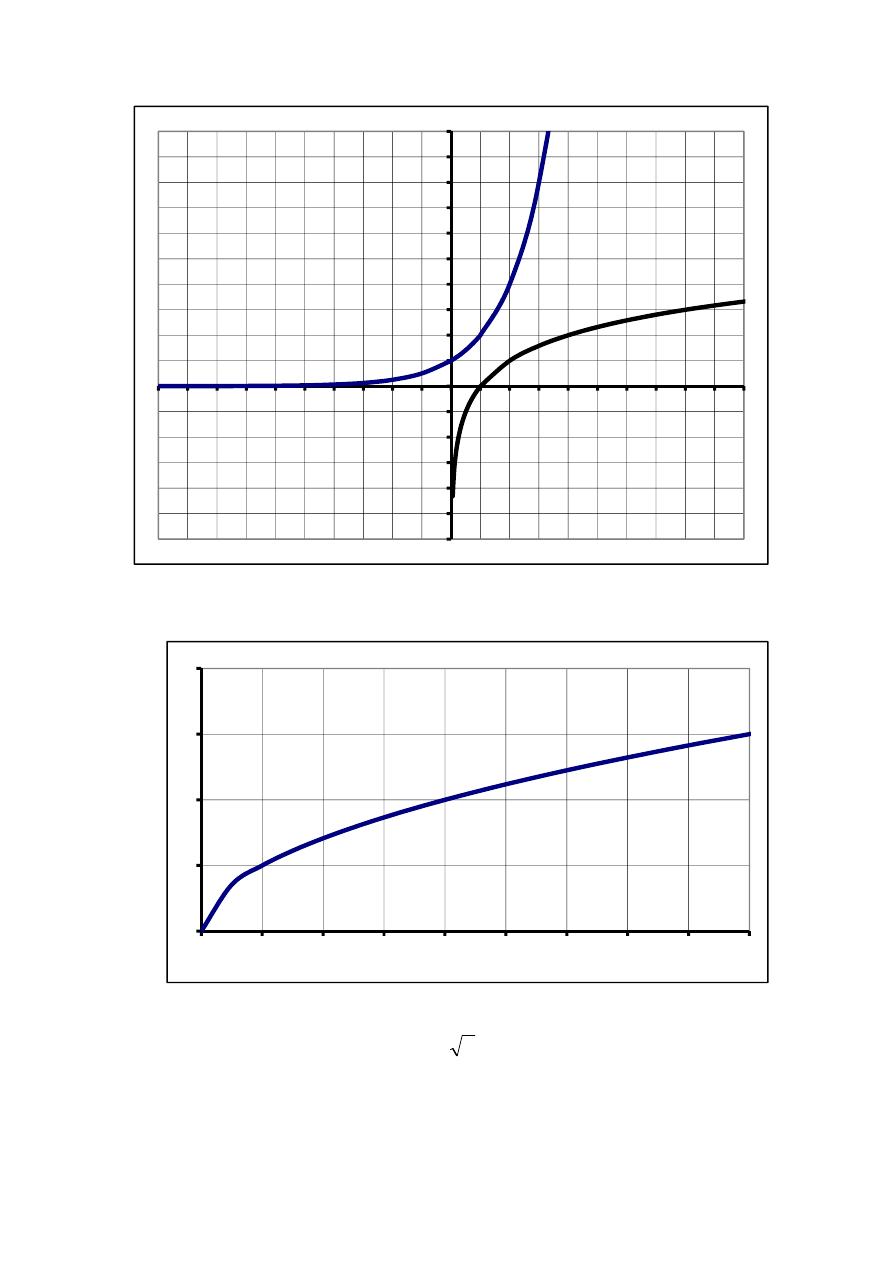
x
y
=
2
1
i
x
y
2
1
log
=
3
x
y
=
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
-4
-3
-2
-1
0
1
2
3
4
5
6
7
-2
-1
0
1
2
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
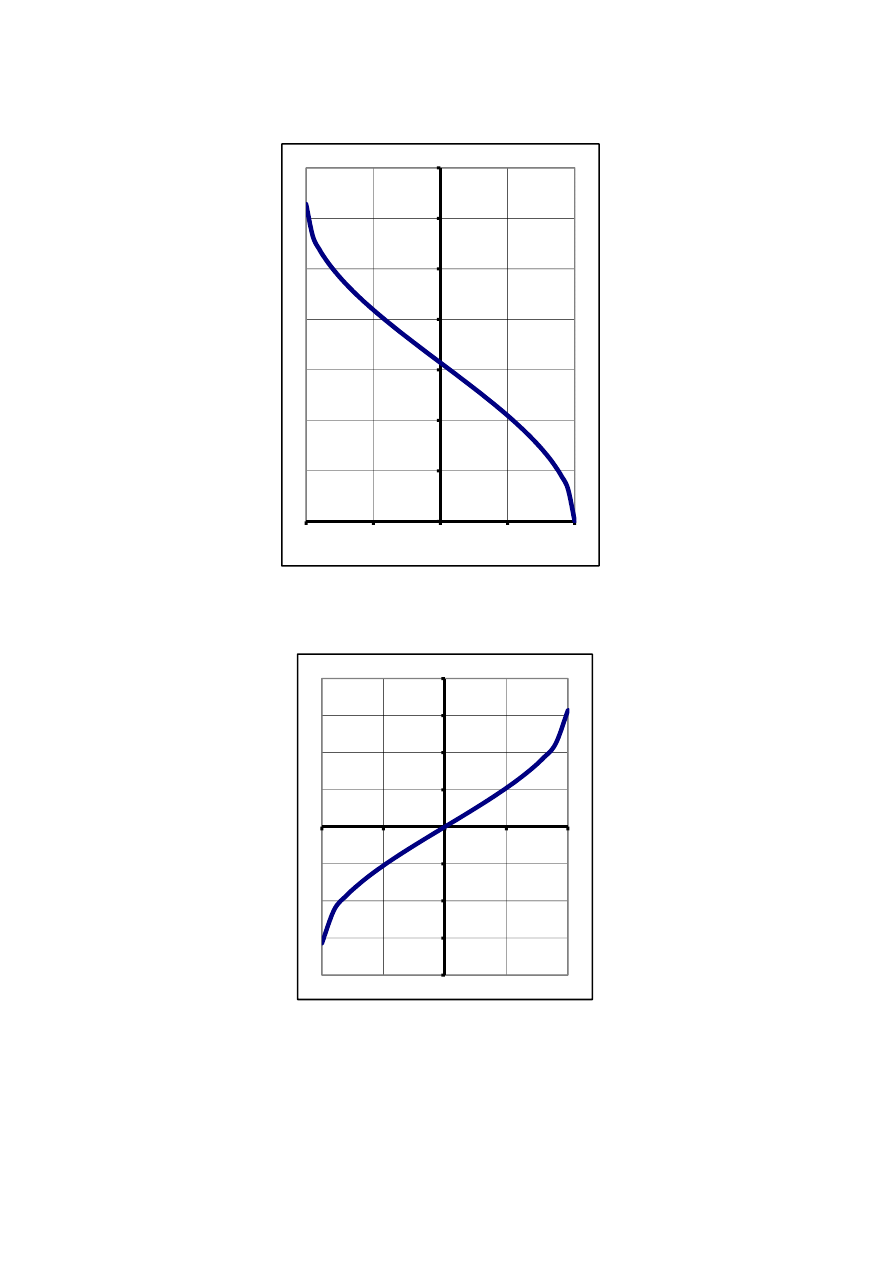
17
x
y
cos
arc
=
x
y
sin
arc
=
0
0,5
1
1,5
2
2,5
3
3,5
-1
-0,5
0
0,5
1
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-1
-0,5
0
0,5
1

18
x
y
tg
arc
=
x
y
ctg
arc
=
-1,5
-1
-0,5
0
0,5
1
1,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
0
0,5
1
1,5
2
2,5
3
3,5
-10 -9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
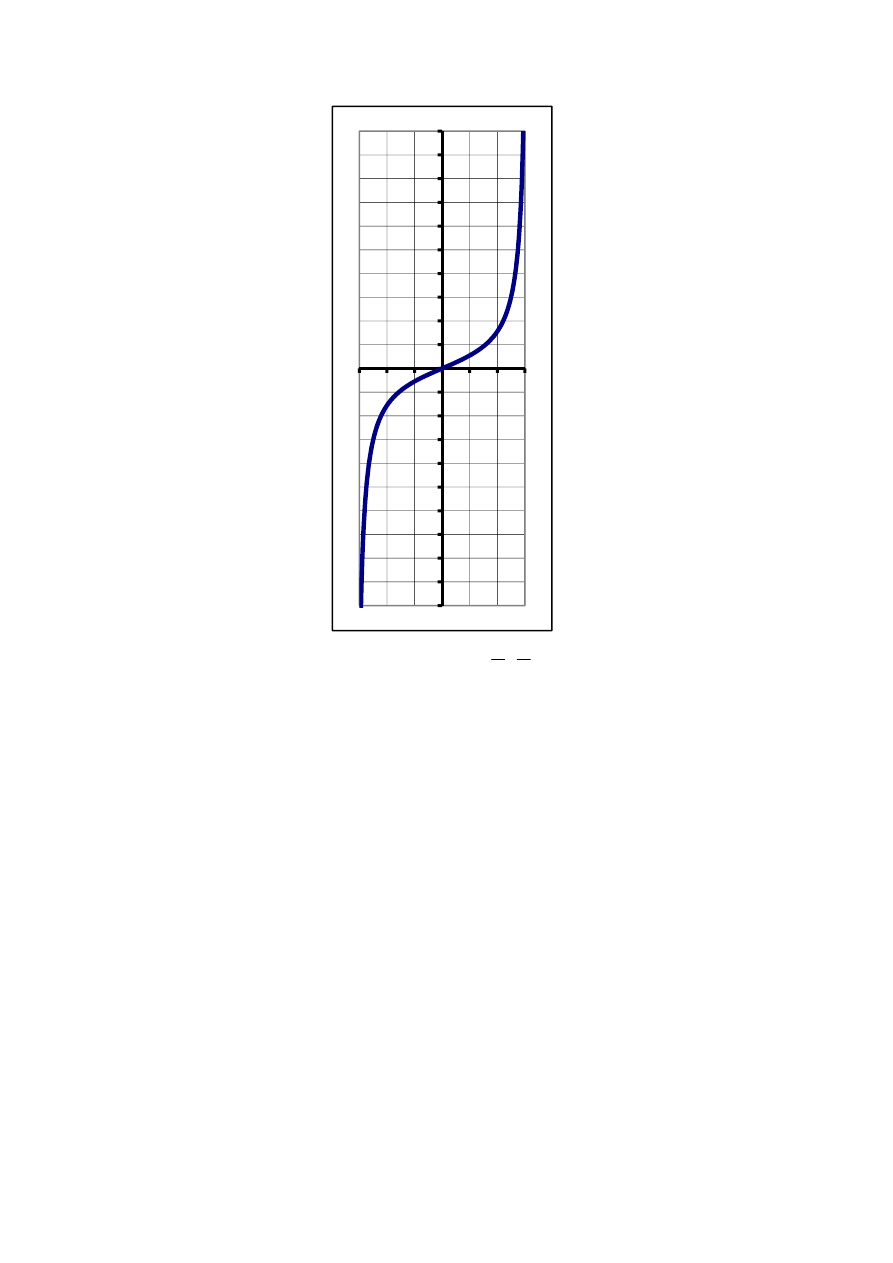
19
x
y
1
=
-1
-0,75
-0,5
-0,25
0
0,25
0,5
0,75
1
-25
-20
-15
-10
-5
0
5
10
15
20
25
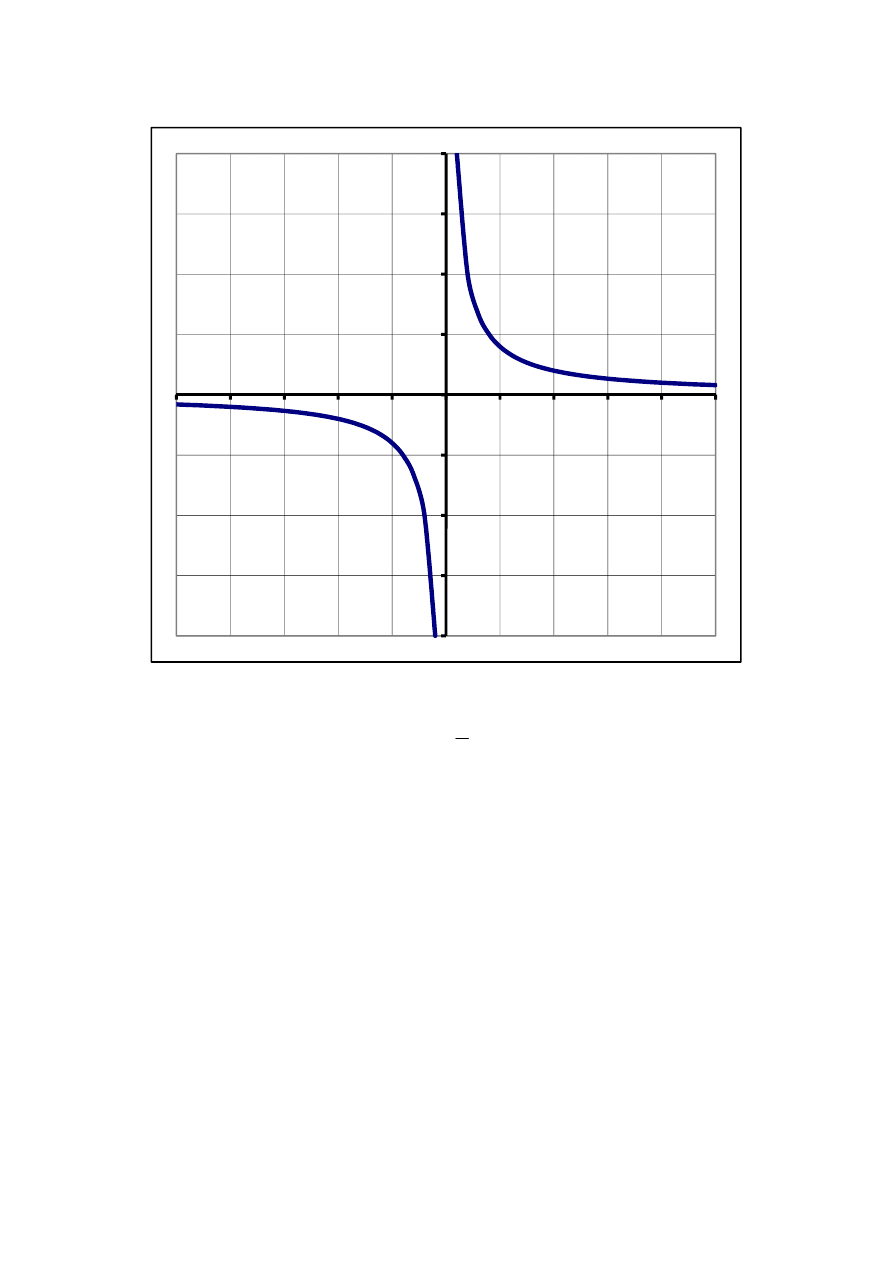
20
x
y
tg
=
,
π
π
−
∈
2
;
2
x
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
-1,5 -1 -0,5 0
0,5
1
1,5
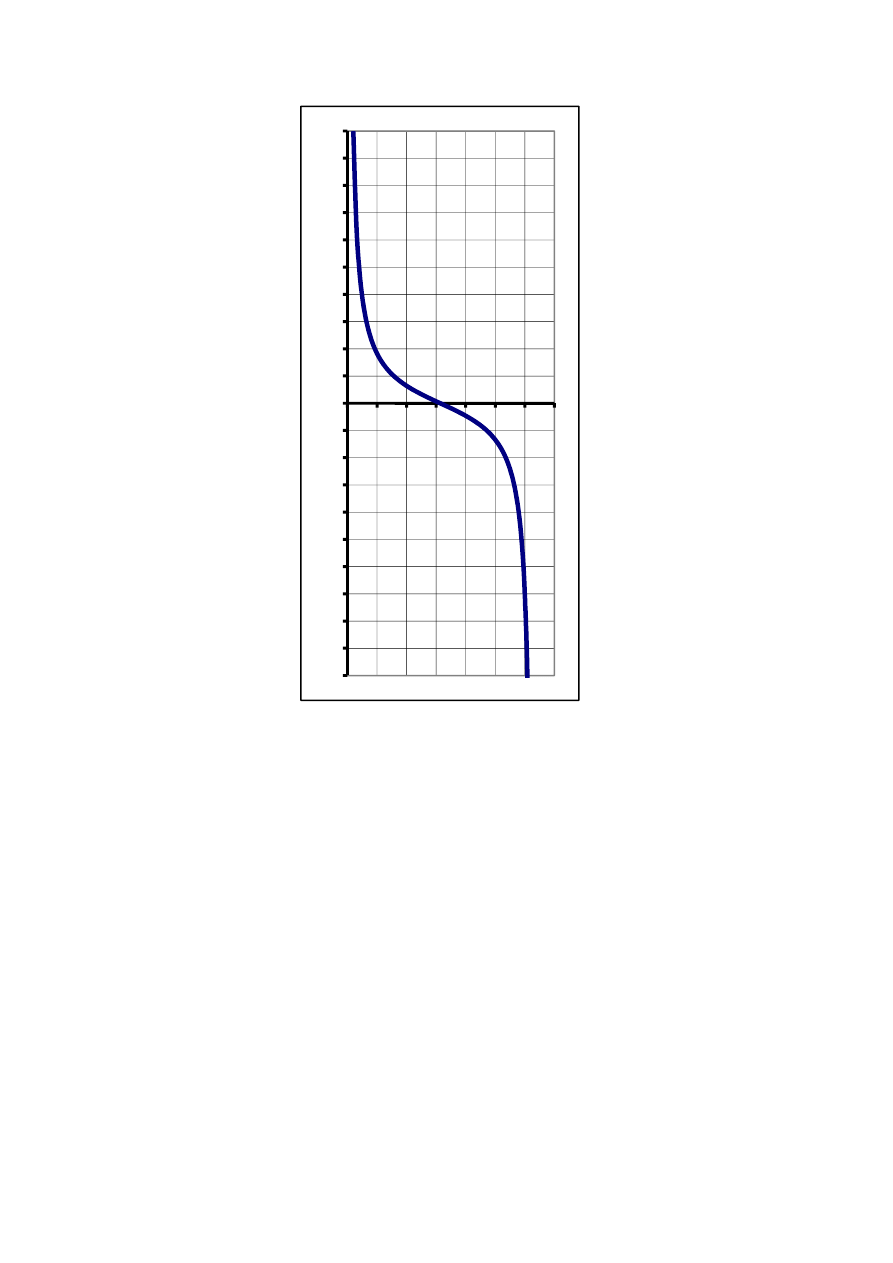
21
x
y
ctg
=
,
)
;
0
(
π
∈
x
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
0
0,5
1
1,5
2
2,5
3
3,5
Wyszukiwarka
Podobne podstrony:
Kombinatoryka matematyka
WYKLAD ANALIZA MATEMATYCZNA
ZABAWA MATEMATYCZNA
Starożytni matematycy
MODEL MATEMATYCZNY TURBINY
Umiejętności matematyczne dzieci w przedszkolu
Matematyka wykład 1
Matematycy
operatory i funkcje matematyczne
Matematyka listopad 2009
Matematyka 2 Lekcje powtórzeniowe w gimnazjum
więcej podobnych podstron