Statystyka w analizie i planowaniu eksperymentu

Wykład 1

Podstawy rachunku prawdopodobieństwa

Przemysław Biecek

Dla 1 roku studentów Biotechnologii

Zasady

Informacje o wykładzie, materiały, ogłoszenia i wyniki kolokwiów
http://www.biecek.pl/statystyka/
W planie jest:

13 wykładów,

2 kolokwia [można zdobyć 2 x 4 punkty],

4 wejściówki [można zdobyć 4 x 1 punkt].

Zaliczenie wykładu już od 5 punktów!

Podstawy rachunku prawdopodobieństwa

2/34

Literatura

1

A. Łomnicki

„Wprowadzenie do statystyki dla przyrodników” PWN 1999.

2

P. Grzegorzewski, K. Bobecka, A. Dembińska, J. Pusz

„Rachunek prawdopodobieństwa i statystyka” WSISiZ 2005.

3

J. Koronacki, J. Mielniczuk

„Statystyka dla studentów kierunków techniczych i przyrodniczych” WNT
2006.

4

M. Jean

„Podstawy Matematyki i Statystyki – dla biologów lekarzy i
farmaceutów” PZWL 1972.

5

J. Jakubowski, R. Sztencel

„Wstęp do teorii prawdopodobieństwa” SCRIPT 2001.

6

J. Jakubowski, R. Sztencel

„Rachunek prawdopodobieństwa dla (prawie) każdego” SCRIPT 2002.

7

C.R. Rao

„Statystyka i prawda” PWT 1994.

Podstawy rachunku prawdopodobieństwa

3/34

Klasyfikacja zmiennych Stevensa

Zmienne jakościowe (nazywane również kategorycznymi,
czynnikowymi), to zmienne przyjmujące określoną liczbę wartości
(najczęściej nie liczbowych),

binarne, np. płeć (kobieta/mężczyzna),
nominalne, np. marka samochodu,
porządkowe, np. wykształcenie (podstawowe / średnie /
wyższe).

Zmienne ilościowe, opisują ilość. Wyróżnia się skale:

licznikową (liczebność wystąpień pewnego zjawiska, opisywana
przez liczby naturalne), np. liczba lat nauki,
przedziałową (nazywana też interwałową), skala w której
zmienna może przyjmować dowolne wartości z określonego
przedziału, np. temperatura w stopniach Celcjusza,
ilorazową, to skala licznikowa, w której dodatkowo zachowane
są proporcje (a więc skala ma zero absolutne), np. temperatura
w stopniach Kelvina, wzrost w centymetrach itp.

Podstawy rachunku prawdopodobieństwa

4/34

Model mechanizmu losowego

Eksperymentem losowym (lub mechanizmem losowym) E
nazywamy eksperyment, który ma następujące właściwości:

wiemy jakie wyniki możemy zaobserwować (zbiór wyników
oznaczamy przez Ω),

nie wiemy, jaki wynik zaobserwujemy,

eksperyment możemy wielokrotnie powtarzać w identycznych
warunkach,

wraz ze wzrostem liczby powtórzeń eksperymentu stabilizują
się odpowiednie częstości.

Podstawy rachunku prawdopodobieństwa

5/34

Prawdpodobieństwo i przestrzeń probabilistyczna

Przestrzeń zdarzeń elementarnych

Przestrzenią zdarzeń elementarnych nazywamy zbiór możliwych
wyników eksperymentu losowego Ω.

Przestrzeń probabilistycza

Przestrzenią probabilistyczną nazywamy trójkę (Ω, F , P), gdzie

Ω to przestrzeń zdarzeń elementarnych,

F to przestrzeń zdarzeń (wybranych podzbiorów Ω),

P to funkcja określająca prawdopodobieństwo wystąpienia
zdarzeń ze zbioru F .

Podstawy rachunku prawdopodobieństwa

6/34

Definicja prawdopodobieństwa (Kołomogorow)

Prawdopodobieństwo

Prawdopodobieństwo to funkcja określona na przestrzeni zdarzeń
F . Prawdopodobieństwo spełnia trzy aksjomaty:

prawdopodobieństwo każdego zdarzenia jest nieujemne,
P(A) ≥ 0,

w wyniku przeprowadzenia eksperymentu zdarzy się któreś ze
zdarzeń, P(Ω) = 1,

prawdopodobieństwa zdarzeń rozłącznych sumują się,
P(A ∪ B) = P(A) + P(B) (dla rozłącznych zdarzeń A i B).

Interpretacja częstościowa (najpopularniejsza):

P(A) =

# wystapien zdarzenia A

# liczba prob

Podstawy rachunku prawdopodobieństwa

7/34

Właściwości prawdopodobieństwa

Wybrane właściwości prawdopodobieństwa:

P() = 0 oraz P(Ω) = 1,

Dla dowolnego zdarzenia A przyjmuje wartości z przedziału
0 ≤ P(A) ≤ 1,

Jeżeli A

0

to zdarzenie przeciwne do A

P(A

0

) = 1 − P(A),

Dla dowolnych dwóch zdarzeń A i B
P(A ∪ B) = P(A) + P(B) − P(A ∩ B).

Jeżeli A ⊂ B to P(A) ≤ P(B).

Podstawy rachunku prawdopodobieństwa

8/34

Przykłady

Rzucamy sześciościenną kostką do gry. Kostka jest uczciwa,
wypadnięcie każdej liczby oczek jest równie prawdopodobne.

Określamy odpowiednie przestrzenie i wartości

Ω = {1, 2, 3, 4, 5, 6},

F - wszystkie podzbiory na Ω,

P(X = 5) = 1/6,

P(X > 4) = P(X = 5) + P(X = 6) = 1/3.

Podstawy rachunku prawdopodobieństwa

9/34

Przykłady

Grupę Rh krwi określa się na podstawie obecności antygenu D
występującego w dwóch allelach, dominującym D i recesywnym d
(to uproszczenie, w rzeczywistości Rh kodowane wielogenowo).
Przyjmuje się, że w rasie białej częstość wstępowania alleli D
wynosi P(D) = 0.61 a d wynosi P(d ) = 0.39. Częstość genotypów
odpowiada równowadze HW a więc 85% populacji ma grupę Rh+.

Rozważmy genotyp osobnika wylosowanego z populacji białej.

Ω = {DD, Dd , dD, dd },

F - wszystkie podzbiory na Ω,

P(DD) = 0.61

2

,

P(DD ∨ Dd ∨ dD) = P(DD) + P(Dd ) + P(dD) =
0.61

2

+ 2 · 0.61 · 0.39 = 0.85.

Podstawy rachunku prawdopodobieństwa

10/34

Prawdopodobieństwo geometryczne

Zdarzeń elementarnych może być nieskończenie wiele, np.
rozważmy przykład:

Prowadzący umawia się ze studentami na konsultacje pomiędzy 9
a 10. Przychodzi w losowej chwili i czeka 15 min. Jeżeli nie spotka
studentów idzie do domu.

Studenci przychodzą w losowej chwili i czekają 15 min. Jeżeli nie
spotkają prowadzącego idą do domu.

Jaka jest przestrzeń Ω?
Jakie zdarzenie odpowiada sytuacji w której studenci spotkają
prowadzącego?
Ile wynosi prawdopodobieństwo wystąpienia tego zdarzenia?

Podstawy rachunku prawdopodobieństwa

11/34

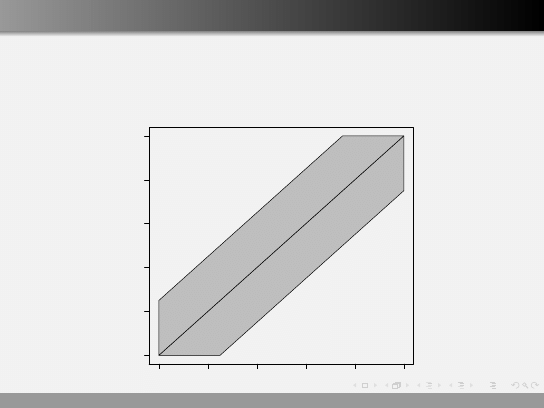
Prawdopodobieństwo geometryczne

Przestrzeń zdarzeń opisuje czasu przyjścia

Ω = [9 : 00, ..., 10 : 00] × [9 : 00, ..., 10 : 00]

9.0

9.2

9.4

9.6

9.8

10.0

9.0

9.2

9.4

9.6

9.8

10.0

studenci

wykladowca

Podstawy rachunku prawdopodobieństwa

12/34

Prawdopodobieństwo warunkowe

Prawdopodobieństwo warunkowe

Prawdopodobieństwo warunkowe odpowiada na pytanie jakie jest
prawdopodobieństwo zdarzenia A, jeżeli wiemy, że zaszło zdarzenie
B?

P(A|B) =

P(A ∩ B)

P(B)

Jeżeli zdarzenia nie zależą od siebie, to

P(A|B) = P(A)

a więc zdarzenia niezależne

P(A ∩ B) = P(A)P(B).

Podstawy rachunku prawdopodobieństwa

13/34

Prawdopodobieństwo warunkowe

Wróćmy do przykładu z grupą Rh.
Jakie jest prawdopodobieństwo wylosowania osoby z genotypem
DD, jeżeli wylosowaliśmy osobę z grupą Rh+?

P(DD|Rh+) =

P(DD ∩ Rh+)

P(Rh+)

=

P(0.61

2

)

0.85

= 0.44

A jakie jest prawdopodobieństwo wylosowania osoby z genotypem
dd , jeżeli wylosowaliśmy osobę z grupą Rh+?

Podstawy rachunku prawdopodobieństwa

14/34

Prawdopodobieństwo całkowite

Układ zupełny zdarzeń

Układ zupełny zdarzeń to zbiór parami rozłącznych zdarzeń,
których suma jest równa Ω.

Prawdopodobieństwo całkowite

Niech zdarzenia H

1

, ..., H

k

∈ F będą układem zupełnym. Wtedy

P(A) =

k

X

i =1

P(A|H

i

)P(H

i

)

Podstawy rachunku prawdopodobieństwa

15/34

Prawdopodobieństwo całkowite

Jak to wygląda w praktyce?
Grupę Rh+ jak już wiemy ma 85% przedstawicieli rasy białej.
W innych rasach ta grupa występuje z prawdopodobieństwem 99%.
Przyjmując, że 25% ludności świata to przedstawiciele rasy białej,
jakie jest prawdopodobieństwo wylosowania człowieka z grupą
Rh+?

P(Rh+) =

P(Rh + |rasa biala)P(rasa biala)+
P(Rh + |rasa inna)P(rasa inna)

=

0.85 ∗ 0.25 + 0.99 ∗ 0.75 = 95.5%

Podstawy rachunku prawdopodobieństwa

16/34

Wzór Bayesa

Wzór Bayesa

Prawdopodobieństwo warunkowe, można również wyznaczyć
z następującego wzoru

P(B|A) =

P(B ∩ A)

P(A)

=

P(A|B)P(B)

P(A)

Łatwo zapamiętać ten wzór ponieważ

P(B|A)P(A) = P(A|B)P(B) = P(A ∩ B)

Uwaga (częste pomyłki)!!!
Wartości P(A|B) i P(B|A) nie muszą być równe!

Podstawy rachunku prawdopodobieństwa

17/34

Wzór Bayesa

Wróćmy do naszego przykładu z Rh+ i rasami.
Znamy częstość występowania grupy krwi Rh+ pod warunkiem, że
jest się przedstawicielem rasy białej.
Jak policzyć prawdopodobieństwo bycia przedstawicielem rasy
białej, pod warunkiem, że ma się grupę Rh+?

P(rasa biala|Rh+)

=

P(Rh+|rasa biala)P(rasa biala)

P(Rh+)

=

=

0.85∗0.25

0.955

= 22%

P(rasa biala|Rh−)

=

P(Rh−|rasa biala)P(rasa biala)

P(Rh−)

=

0.15∗0.25

0.045

= 83%

Podstawy rachunku prawdopodobieństwa

18/34

Niezależność zdarzeń

Jak pamiętamy zdarzenia są niezależne, jeżeli

P(A ∩ B) = P(A)P(B).

Czy posiadanie grupy Rh+ i Rh- to zdarzenia niezależne?

Czy posiadanie grupy Rh+ i bycie przedstawicielem rasy białej
to zdarzenia niezależne ?

Czy otrzymanie allela D od matki i allela D od ojca to
zdarzenia niezależne ?

Podstawy rachunku prawdopodobieństwa

19/34

Zmienna losowa

Nie wygodnie jest posługiwać się nazwami zdarzeń. Potrzebujemy
„czegoś” żeby o zdarzeniach losowych mówić w terminach wartości
liczbowych.

Zmienna losowa

Zmienną losową X nazywamy funkcje przekształcającą zbiór
zdarzeń elementarnych Ω na zbiór liczb rzeczywistych R.

Przykład:
Określamy zmienną losową X jako liczbę alleli D w genotypie
wylosowanego osobnika. Taka zmienna losowa może przyjąć
wartości 0, 1 lub 2.

Podstawy rachunku prawdopodobieństwa

20/34

Dystrybuanta rozkładu

Dystrybuanta rozkładu zmiennej losowej X

Rozkład zmiennej losowej można opisać dystrybuantą, czyli funkcją
zmiennej losowej X zdefiniowaną następująco

F (X ) = P(ω ∈ Ω : X (ω) ≤ x )

Dystrybuanta jest funkcją:

niemalejącą,

z przedziału [0, 1],

o wartościach lim

x →−∞

F (x ) = 0 i lim

x →∞

F (x ) = 1,

oraz dla której P(a < X ≤ b) = F (b) − F (a).

Podstawy rachunku prawdopodobieństwa

21/34

Zmienne skokowe i ciągłe

Zmienne losowe można podzielić na dwie grupy:

Zmienne skokowe (dyskretne), które przyjmują skończoną
(przeliczalną) liczbę wartości. Dla każdej wartości możemy
wyznaczyć prawdopodobieństwo jej wystąpienia (np. liczba
studentów, liczba alleli, liczba oczek na kostce).

Zmienne ciągłe, mogą przyjmować nieskończoną liczbę
wartości (np. ilość wody w wiadrze, waga osobnika,
temperatura za oknem).

Podstawy rachunku prawdopodobieństwa

22/34

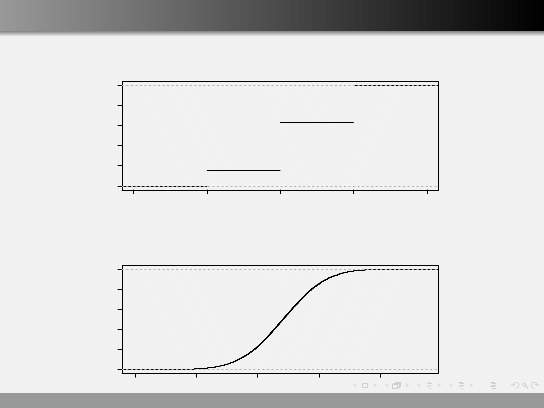
Zmienne skokowe i ciągłe

−1

0

1

2

3

0.0

0.2

0.4

0.6

0.8

1.0

liczba alleli D

x

dystrybuanta

●

●

●

10

15

20

25

30

0.0

0.2

0.4

0.6

0.8

1.0

współczynnik BMI

x

dystrybuanta

Podstawy rachunku prawdopodobieństwa

23/34

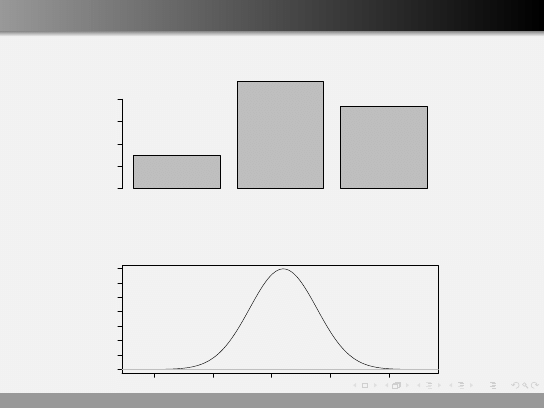
Zmienne skokowe i ciągłe

0

1

2

liczba alleli D

0.0

0.1

0.2

0.3

0.4

0

10

20

30

40

0.00

0.02

0.04

0.06

współczynnik BMI

x

gę stoś ć

Podstawy rachunku prawdopodobieństwa

24/34

Zmienne o rozkładzie ciągłym

Wybrane rozkłady ciągłe, które pojawią się na kolejnych
wykładach.

Rozkład normalny (najpopularniejszy, często używany, można
go otrzymać z innych rozkładów),

Rozkład jednostajny (intuicyjny równoważnik słowa losowy),

Rozkład F,

Rozkład χ

2

.

Podstawy rachunku prawdopodobieństwa

25/34

Zmienne o rozkładzie dyskretnym

Wybrane rozkłady dyskretne, które pojawią się na kolejnych
wykładach.

Rozkład Bernoulliego (rzut monetą),

Rozkład dwumianowy (rzut wieloma monetami),

Rozkład Poissona (liczba sygnałów),

Rozkład hipergeometryczny (kule w urnach).

Podstawy rachunku prawdopodobieństwa

26/34

Momenty zwykły i centralny (wzory dla zmiennych
skokowych)

Momenty to charakterystyki rozkładu, opisują jego wybrane
właściwości.
Moment r zwykły

EX

r

=

k

X

i =1

x

r

i

p

i

.

Moment r centralny

EX

r

c

=

k

X

i =1

(x

i

− µ)

r

p

i

.

Podstawy rachunku prawdopodobieństwa

27/34

Wybrane charakterystyki (wzory dla zmiennych skokowych)

Wartość średnia (wartość oczekiwana, parametr położenia)

µ = EX =

k

X

i =1

x

i

p

i

.

Wariancja (miara rozproszenia, parametr skali)

σ

2

= EX

2

c

=

k

X

i =1

(x

i

− µ)

2

p

i

.

Skośność

γ =

k

X

i =1

(x

i

− µ)

3

p

i

/σ

3

.

Kurtoza (parametr skupienia)

η =

k

X

i =1

(x

i

− µ)

4

p

i

/σ

4

.

Podstawy rachunku prawdopodobieństwa

28/34

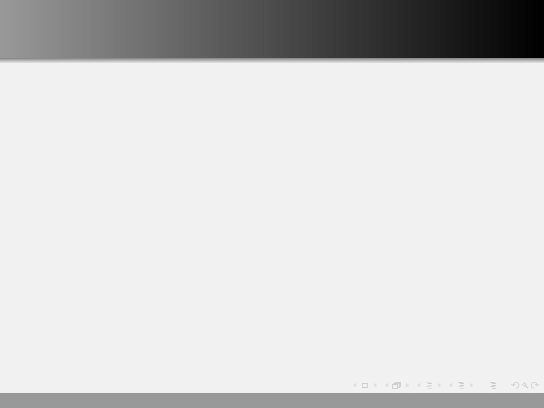
Różnice w charakerystykach położenia i skali

−4

−2

0

2

4

0.0

0.1

0.2

0.3

0.4

róż nica w ś redniej

x

gę stoś ć

−4

−2

0

2

4

0.0

0.1

0.2

0.3

0.4

róż nica w wariancji

x

gę stoś ć

Podstawy rachunku prawdopodobieństwa

29/34

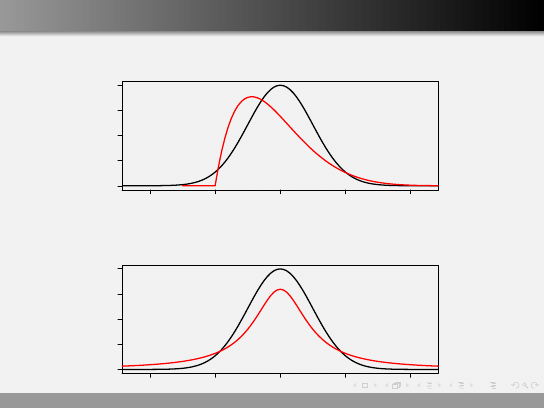
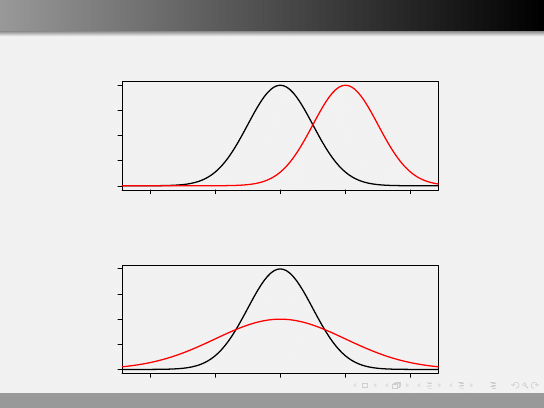
Różnice w charakerystykach kształtu

−4

−2

0

2

4

0.0

0.1

0.2

0.3

0.4

róż nica w skoś noś ci

x

gę stoś ć

−4

−2

0

2

4

0.0

0.1

0.2

0.3

0.4

róż nica w kurtozie

x

gę stoś ć

Podstawy rachunku prawdopodobieństwa

30/34

Parametry rozkładu, cz. 1

Dla każdego rozkładu wyznaczyć można następujące
charakterystyki:

dziedzina (przedział zmienności), czyli zbiór w jakim wartości
przyjmuje zmienna losowa,

średnia obcięta (Windsordzka),

wariancja σ

2

,

odchylenie standardowe σ,

współczynnik zmienności CV (coefficient of variance) σ/µ,

moda (dominanta).

Podstawy rachunku prawdopodobieństwa

31/34

Parametry rozkładu, cz. 2

kwantyl rzędu q, to wartość x dla której dystrybuanta
zmiennej losowej przyjmuje wartość q,

mediana (wartość środkowa), kwantyl rzędu 1/2,

kwartyl dolny to kwantyl rzędu 1/4, kwartyl górny to kwantyl
rzędu 3/4,

percentyl rzędu p to kwantyl rzędu p/100,

rozstęp między kwartylowy (IQR) to różnica pomiędzy q

0.75

a

q

0.25

,

odchylenie medianowe MAD
1.4826 ∗ median(|x

i

− median(x

i

)|).

Podstawy rachunku prawdopodobieństwa

32/34

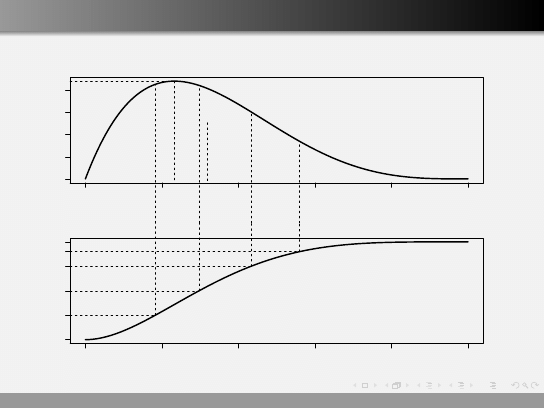
Parametry rozkładu

0.0

0.2

0.4

0.6

0.8

1.0

0.0

0.5

1.0

1.5

2.0

gestoś ć

moda

ś rednia

*

0.0

0.2

0.4

0.6

0.8

1.0

dystrybuanta

0.00

0.25

0.50

0.75

0.90

1.00

1 kwartyl

mediana

3 kwartyl

kwantyl 90%

Podstawy rachunku prawdopodobieństwa

33/34

Co trzeba zapamiętać?

Co oznaczają terminy:
prawdopodobieństwo, zdarzenie, zdarzenie elementarne ?

Jakie właściwości ma prawdopodobieństwo?

Co oznacza oraz jak liczyć prawdopodobieństwo warunkowe i
całkowite?

Do czego służy wzór Bayesa?

Co ozancza niezależność zdarzeń?

Co opisuje dystrybuanta a co gęstość?

Jakimi parametrami opisuje się rozkłady?

Podstawy rachunku prawdopodobieństwa

34/34