Wyznaczanie logarytmicznego dekrementu

tłumienia wahadła fizycznego

Przyrządy:

1. Wahadło fizyczne.
2. Stoper.
3. Przymiar milimetrowy.

Przebieg czynności:

1. Umieścić przymiar milimetrowy na stole tak, aby zero skali pokrywało się z

położeniem równowagi wahadła.

2. Pięciokrotnie wyznaczyć czas pełnych 20 wahnięć wahadła zamkniętego

20

t . Obliczyć

wartość średnią

20

t .

3. Korzystając ze wzoru:

20

20

t

T



obliczyć okres drgań wahadła zamkniętego.

4. Wychylić wahadło z położenia równowagi o

cm

25



A

. Odczytywać ze skali,

z dokładnością do 1mm, kolejne wychylenia A wahadła z obu stron położenia
równowagi w ciągu 10 okresów. Pomiary powtórzyć dwukrotnie. Wyniki umieścić w
tabeli i obliczyć wielkości średnie A . Na podstawie znajomości okresu T , obliczyć
wartości czasu

t , odpowiadające poszczególnym wychyleniom.

5. N podstawie definicji

 





















T

t

A

t

A

ln



obliczyć wartość logarytmicznego dekrementu tłumienia



dla kolejnych czasów

t

oraz ich wartość średnią

def



.

6. Sporządzić wykres zależności

 

A

ln

od czasu. Za pomocą regresji liniowej

wyznaczyć współczynnik tłumienia



:

 

 

b

x

a

y

A

t

A















0

ln

ln



Obliczyć:



współczynnik oporu ośrodka:

m

B



2



(

g

361



m

– masa wahadła),



czas relaksacji:





1



reg

,



logarytmiczny dekrement tłumienia:

T

reg







.

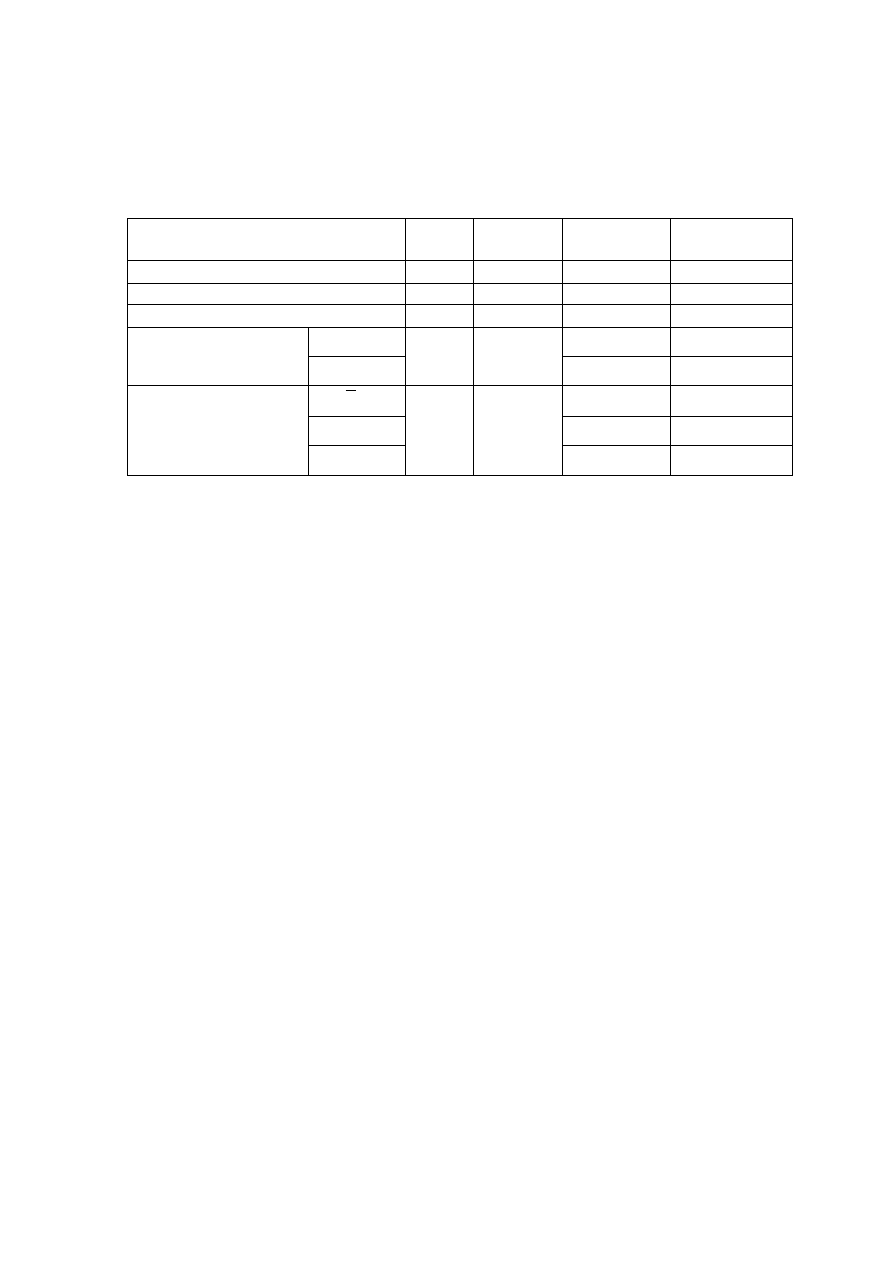
7. Wykreślić zależność wychylenia wahadła od czasu oraz krzywą tłumienia. Z wykresu

odczytać czas relaksacji

wyk



oraz logarytmiczny dekrement tłumienia

wyk



.

8. Powtórzyć czynności wykonane w punktach 2 – 7 dla wahadła otwartego.
9. Otrzymane wyniki zestawić w tabelce:

Wielkość

Symbol Jednostka

Wahadło

otwarte

Wahadło

zamknięte

współczynnik tłumienia





współczynnik oporu ośrodka

okres drgań





czas relaksacji



reg







wyk



logarytmiczny

dekrement tłumienia

def





reg



wyk



10. Zanotować wnioski.

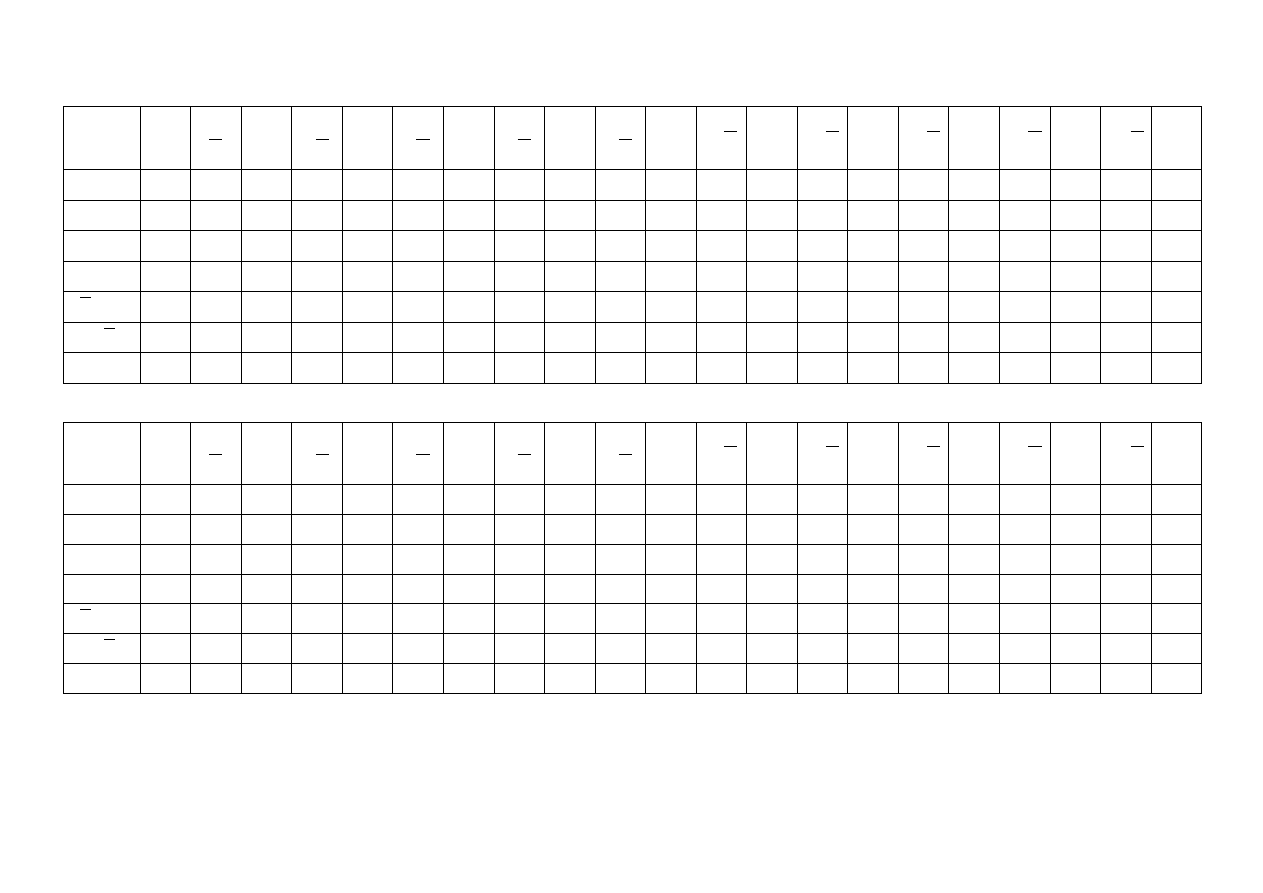
Tabele pomiarowe:

1. Wahadło zamknięte:

0

2

T

T

2

3

T

T

2

2

5

T

T

3

2

7

T

T

4

2

9

T

T

5

2

11

T

T

6

2

13

T

T

7

2

15

T

T

8

2

17

T

T

9

2

19

T

T

10

 

s

t

 

cm

1

A

 

cm

2

A

 

cm

3

A

 

cm

A

 

A

ln



–

–

2. Wahadło otwarte

0

2

T

T

2

3

T

T

2

2

5

T

T

3

2

7

T

T

4

2

9

T

T

5

2

11

T

T

6

2

13

T

T

7

2

15

T

T

8

2

17

T

T

9

2

19

T

T

10

 

s

t

 

cm

1

A

 

cm

2

A

 

cm

3

A

 

cm

A

 

A

ln



–

–