Populacja generalną

nazywamy zbiór elementów powiązanych ze sobą 

logicznie i jednocześnie nieidentycznych ze względu na badana cechę.

Próbą statystyczną

nazywamy podzbiór populacji generalnej podlegający 

bezpośrednio obserwacji w celu zbadania własności całej populacji.

Próbą losową

nazywany próbę otrzymaną w drodze losowania, czyli jedynie 

przypadek decyduje o tym, że dany element (obiekt) populacji generalnej znajdzie się 
w próbie.

W praktyce przy losowaniu prób korzysta się często z  tablic liczb losowych. 

Jednostki statystyczne wchodzące w skład zbiorowości statystycznej są 

jednorodne, tzn. mają cechy wspólne oraz własności takie, które różnicuję te 

jednostki między sobą. 

Cechą statystyczna

nazywamy własnośd, którą 

charakteryzuje się każda jednostka statystyczna.

Cechy dzielimy na:

 stałe 

– własności wspólne dla wszystkich jednostek danej 

zbiorowości statystycznej,

 zmienne

– własności dzięki którym poszczególne jednostki różnią się 

między sobą.

Ważnym podziałem cech statystycznych jest podział na cechy:

 mierzalne

– dające się wyrazid za pomocą liczb mianowanych,

 niemierzalne

– własności cech statystycznych nie dające się 

zmierzyd.

Warianty cech statystycznych:

 zmiennośd skokowa

– ma miejsce wtedy, gdy cecha przyjmuje 

skooczoną liczbę wartości liczbowych,

 zmiennośd ciągła

– przyjmuje dowolne wartości liczbowe należące 

do pewnego przedziału liczbowego.

Przykład.

Skala nominalna

: płed, kolor, numer telefonu, numer na koszulce

zawodnika

Skala porządkowa:

kategorie zakładów hotelarskich, skala Likerta (1-w 

pełni się zgadzam, 2-zgadzam się, 3-nie mam zdania, 4- nie zgadzam 
się, 5- absolutnie się nie zgadzam), stopnie wojskowe, stopnie 
żeglarskie, skala 10 punktowa Apgar opisująca stan noworodka w 
pierwszej minucie po porodzie

Skala porządkowa jest często wykorzystywana w badaniach
ankietowych.

Skala interwałowa:

temperatura,

Skala ilorazowa:

wzrost, waga, powierzchnia, długośd.

Charakterystykami (statystykami) 

liczbowymi próby nazywamy wszelkie 
wielkości liczbowe wyznaczone 
z elementów tej próby. 

Istnieją  różne  kryteria  podziału  charakterystyk 

liczbowych  próby.  Jednym  z  nich  jest  podział  ze 

względu  na  udział  obserwacji  próby  przy  ich 

wyznaczaniu. Można wyróżnić: 

 miary  klasyczne  -  do  wyznaczania,  których 

wykorzystuje się wszystkie jednostki próby, 

 miary  pozycyjne  -  do  wyznaczania,  których 

wykorzystuje  się niektóre  (wybrane)  jednostki próby 

uporządkowanej niemalejąco lub nierosnąco.  

 

Wskaźnik struktury informuje, jaki jest udział 

jednostek statystycznych posiadających i-ty 

wariant  (wartośd) cechy w całej badanej 

zbiorowości. Jeśli  przemnożymy przez 100, to 

otrzymamy udziały procentowe.

Średnia jest

wypadkową wszystkich wartości

badanej cechy, w związku z czym nie może byd
niższa od najmniejszej wartości zaobserwowanej
w badaniu i nie może byd wyższa od wartości
największej.

Suma odchyleo wartości badanej cechy od

średniej arytmetycznej jest równa zeru.

Kwartyl pierwszy

(Q

1

) jest to wartośd jednostki, 

która dzieli szereg w taki sposób, że 1/4 jednostek ma 

od niej wartości nie większe, a 3/4 nie mniejsze. 

Kwartyl trzeci

(Q

3

) to taka wartośd, od której 3/4 

jednostek zbiorowości ma wartości nie większe od Q

3

, 

a 1/4 nie mniejsze. 

Dominanta (moda, wartośd dominująca)

Dominantą (D

o

) nazywamy taką wartośd

zmiennej, której odpowiada największa liczba
wartości, czyli jest ona najczęściej występującą
wartością zmiennej, reprezentującej określony
wariant (wartośd) badanej cechy. Dominanta jest
wygodną charakterystyką zbiorowości. Można ją
stosowad zarówno do cech niemierzalnych jak
i mierzalnych.

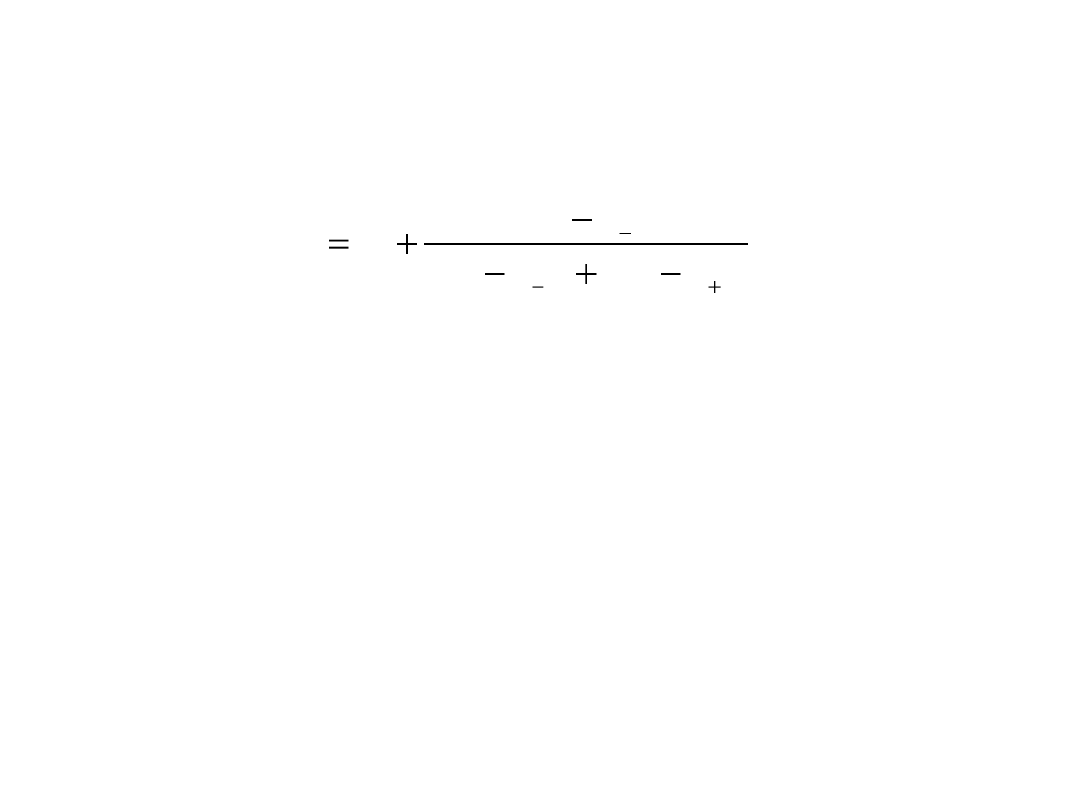
W celu wyznaczenia przybliżonej wartości dominanty 

na podstawie szeregu rozdzielczego o przedziałach 

klasowych wielojednostkowych korzysta się 

z następującego wzoru: 

gdzie:

x

0

- dolna granica przedziału dominanty,

n

0

- liczebnośd przedziału dominanty,

n

-1

- liczebnośd przedziału poprzedzającego przedział 

dominanty,

n

+1

- liczebnośd przedziału następującego po przedziale 

dominanty,

h

0

- rozpiętośd przedziału dominanty.

o

1

o

1

o

1

o

0

h

)

n

(n

)

n

(n

n

n

D

0

x

Należy podkreślid, że dominantę można wyznaczyd tylko 

wtedy, jeśli są spełnione  warunki:

1.

Rozkład musi mied jeden wyraźnie zaznaczony ośrodek 
dominujący (wyraźne skupienie największej części 
jednostek wokół jednej wartości),

2.

Szereg nie może byd skrajnie asymetryczny z otwartym 
przedziałem dominującym (ostatnim lub pierwszym w 
szeregu).