Miary położenia

Miary położenia opisują umiejscowienie typowych
wartości cechy statystycznej na osi liczbowej.

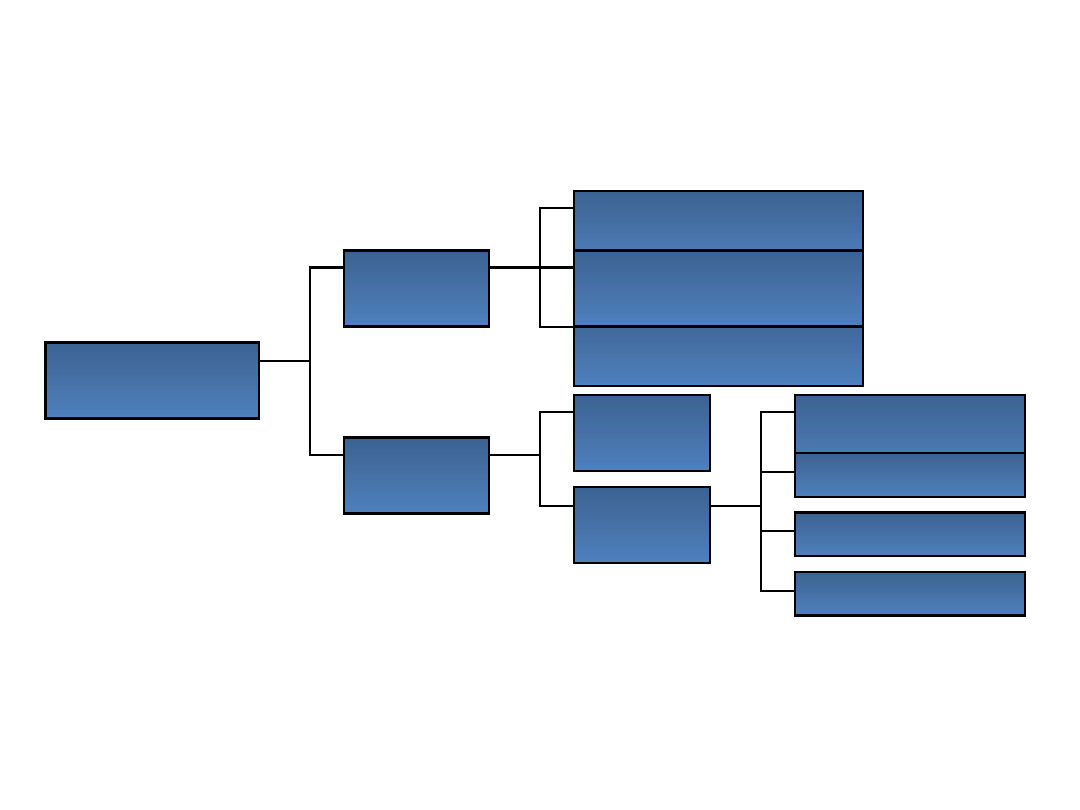
Miary położenia

miary

położenia

pozycyjn

e

klasyczn

e

średnia

arytmetyczna

modaln

a

średnia

geometryczna

średnia

harmoniczna

kwantyl

e

kwartyl

pierwszy

mediana

centyle

kwartyl trzeci

Miary położenia

•Miary klasyczne

, to miary, których wartość jest wyznaczona w oparciu

o wszystkie obserwacje.

•Miary pozycyjne

, to miary, na których wartość wpływają tylko

wybrane obserwacje z próby uporządkowanej.
•Poszczególne rodzaje średnich są obliczane na podstawie wszystkich

wartości przyjmowanych przez cechę w badanej zbiorowości.
•Dla każdego konkretnego przypadku powinno się obliczać tylko jedną

średnią, bo tylko jedna z nich jest odpowiednia dla danej cechy

statystycznej, a pozostałe nie mają sensu.
•Wartość modalna, jest tym wariantem cechy statystycznej, który był

najczęściej obserwowany.
•Kwantyle to takie warianty cechy statystycznej, które dzielą badaną

zbiorowość na części w określonych proporcjach, np. na połowy

(mediana).

•Wśród miar położenia można wyróżnić

miary przeciętne

lub inaczej

miary tendencji centralnej

wskazujące średni lub typowy poziom

cechy, które mówią o przeciętnym poziomie badanej cechy (średnie,
modalna, mediana).

Średnia arytmetyczna

•Średnia arytmetyczna jest najczęściej

wykorzystywaną miarą spośród klasycznych miar

położenia. Inne średnie wykorzystywane są

zdecydowanie rzadziej. Jest stosunkowo prosta do

obliczenia. Jej wadą (wynikającą z tego, że w jej

wyznaczaniu uwzględniane są wszystkie pomiary)

jest wrażliwość na

przypadki odstające

. Przypadki

odstające to pomiary, których wartość

zdecydowanie odbiega od większości pozostałych.

Zwykle są wynikiem błędów, np. błędów przy

zapisywaniu przecinka (wzrost osoby 1,76 cm

zamiast 176 cm).

•Średnią arytmetyczną wyznacza się ze wzoru:

n

x

x

x

n

x

x

n

n

i

i















...

2

1

1

Średnia arytmetyczna

•Przykład:

•Dwóch lekarzy bada pacjentów. Przeprowadzono

obserwację czasu trwania tych badań w minutach.

Zanotowano następujące wyniki:

•Dla lekarza A: 12, 15, 15, 18, 20

•Dla lekarza B: 10, 10, 12, 12, 15, 15, 18, 20, 21, 21

•Korzystając ze wzoru uzyskujemy:

min

4

,

15

10

154

10

21

21

20

18

15

15

12

12

10

10

min

16

5

80

5

20

18

15

15

12







































B

A

x

x

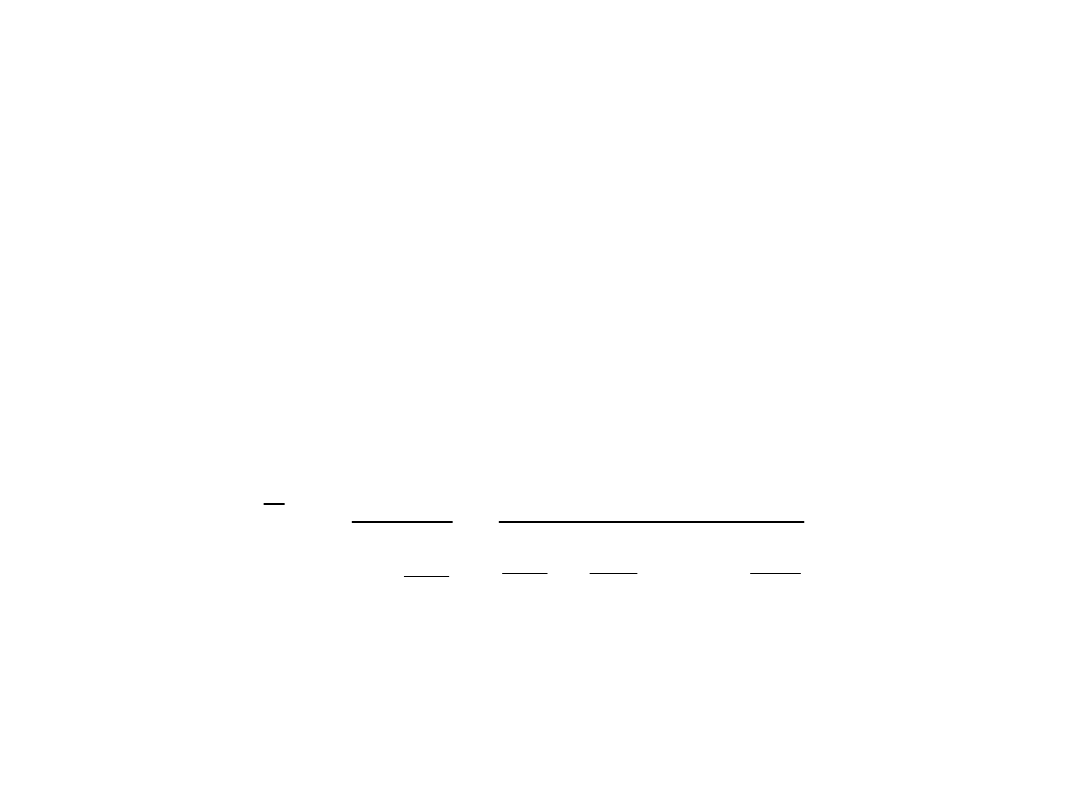
Średnia harmoniczna

•Średnia harmoniczna jest stosowana zdecydowanie

rzadziej niż arytmetyczna. Konieczność jej użycia

zachodzi, gdy wartości cechy statystycznej podawane

są w przeliczeniu na stałą jednostkę innej zmiennej, np.

prędkość w km/h, gęstość zaludnienia w osobach/km

2

,

spożycie w kg/osobę, itp.

•Średnią harmoniczną można wyznaczyć ze wzoru:

n

n

i

i

H

x

x

x

n

x

n

x

1

...

1

1

1

2

1

1















Średnia harmoniczna

•Przykład:
•W ciągu 8 godzin pracy w przychodni obserwowano

pracę trzech pielęgniarek. Na wykonanie obowiązków

związanych z jednym pacjentem pielęgniarka A

potrzebowała 4 min pielęgniarka B – 6 min, a

pielęgniarka C – 12 min. Jaki jest średni czas zużywany

na jednego pacjenta? (proszę zwrócić uwagę na

rzeczywistą jednostkę badanej cechy: min/osobę!!!)

min

6

12

1

6

1

4

1

3









H

x

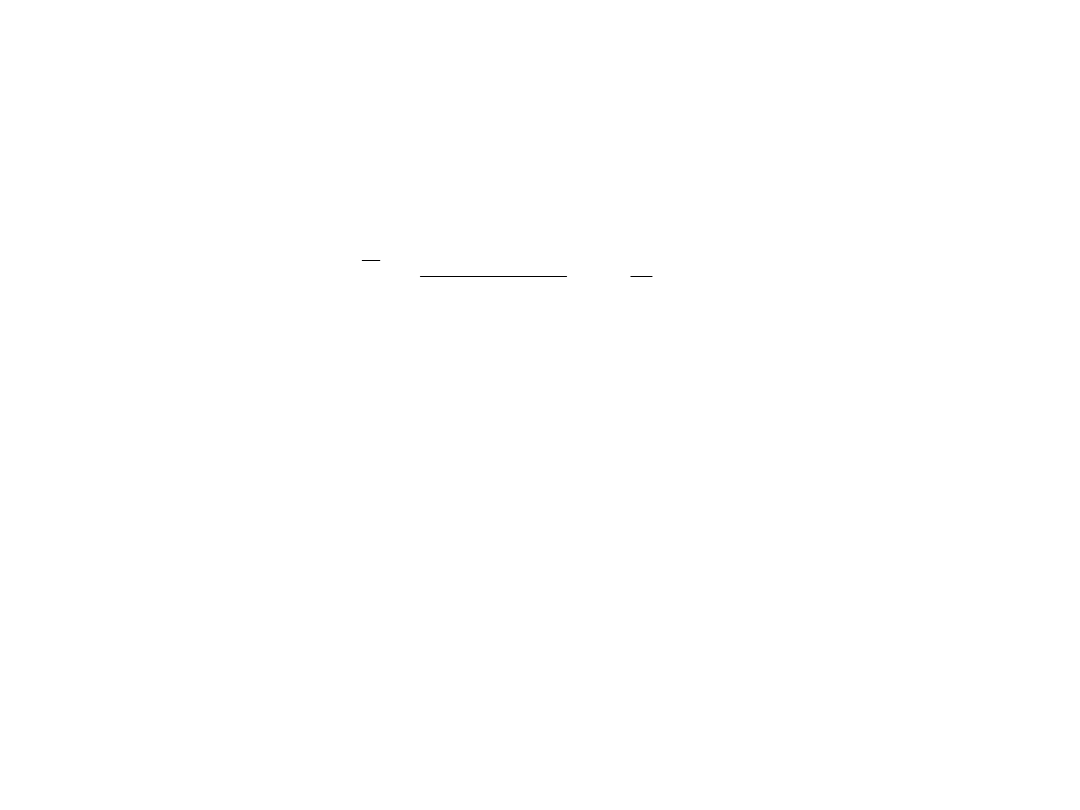
Średnia harmoniczna

•Gdyby w omawianym przykładzie zastosować

średnią arytmetyczną uzyskalibyśmy inny wynik:

min

3

1

7

3

12

6

4









x

Jest to wynik nieprawidłowy, bo przy takim tempie
pracy, trzy pielęgniarki w ciągu 8 godzin (480 minut)
obsłużyłyby 3×480÷7,333 min=196 osób. W
rzeczywistości jednak, pielęgniarka A mogłaby zająć się
480÷4=120 pacjentami, pielęgniarka B - 480÷6=80, a
pielęgniarka C - 480÷12=40, co daje łącznie
120+80+40=240 pacjentów.

Średnia geometryczna

•Średnią geometryczną stosuje się przy badaniu średniego

tempa zmian zjawisk, tzn. w sytuacji, gdy zjawiska są

ujmowane w sposób dynamiczny.
•Średnią geometryczną wyznacza się korzystając ze wzoru:

n

n

n

n

i

i

G

x

x

x

x

x















...

2

1

1

Średnia geometryczna

•Przykład:

•W ciągu trzech kolejnych lat liczba osób

nowozakażonych wirusem HIV wynosiła odpowiednio:

500, 750, 825. Jaki był średni względny przyrost liczby

nowych zakażeń?

•Wartości cechy statystycznej w tym zadaniu to

przyrosty liczby zakażeń w kolejnych latach, tzn.:

1

,

1

750

825

5

,

1

500

750

2

1









x

x

Zgodnie ze wzorem, średni przyrost, to:

28

,

1

1

,

1

5

,

1







G

x

Średnia geometryczna

•Gdyby w tym przykładzie zastosować
średnią arytmetyczną uzyskalibyśmy
wynik: (1,5+1,1)÷2=1,3. Wynikałoby z
tego, że w 3 roku, powinno być
500×1,3×1,3=845 osób
nowozakażonych.

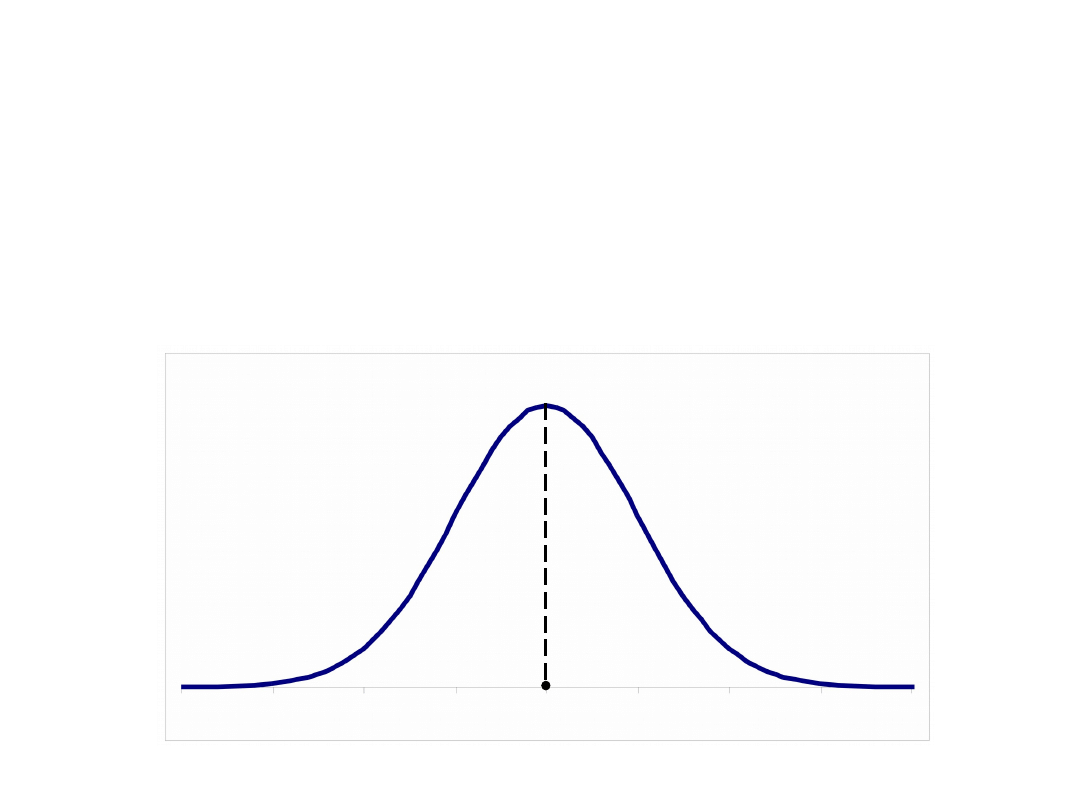
Modalna

Wartość modalna, określana także jako dominanta,
moda lub wartość najczęstsza, to wartość cechy
statystycznej, która w danym rozkładzie empirycznym
występuje najczęściej, a zatem jest to maksimum
funkcji rozkładu empirycznego cechy statystycznej.

Mo

Modalna

•Przykład:

•Wykorzystując dane z przykładu dla średniej

arytmetycznej (czasy badania pacjentów):

•Dla lekarza A: 12, 15, 15, 18, 20

•Dla lekarza B: 10, 10, 12, 12, 15, 15, 18, 20, 21, 21

•W przypadku lekarza A wartością modalną jest czas 15

minut. W przypadku lekarza B nie możemy określić

wartości modalnej, ponieważ żadna z wartości cechy nie

przyjęła pozycji dominującej (cztery wartości cechy

powtarzały się dwukrotnie).

•Jeśli przyjmiemy, że próbę stanowiły łączne wyniki

pracy obu lekarzy, to modalną jest wartość 15

(występująca w tym przypadku 4 razy):

•Mo=15 min

Modalna

•Wartość modalna, jako miara pozycyjna, jest odporna na

występowanie przypadków odstających. Jeśli przykładowo

następujące dane (czas pobytu pacjenta w szpitalu w dniach):

•6, 7, 8, 8, 9, 11, 11, 11, 14, 14, 15, 16, 117

•To średni czas pobytu wyniósłby

(6+7+8+8+9+11+11+11+14+14+15+16+117)÷13=19 dni

•Pomimo, że hospitalizacje nie były dłuższe niż 16 dni (poza

jednym pacjentem, który z jakiejś przyczyny był leczony

bardzo długo), wartość średniej arytmetycznej jest

stosunkowo wysoka. Jest ona silnie zawyżana przez jeden

przypadek odstający. Gdyby jednak do opisania typowego

czasu hospitalizacji użyć wartości modalnej, uzyskamy wynik

11 dni, który jest zbliżony do czasy hospitalizacji prawie

wszystkich pacjentów (poza jednym przypadkiem

odstającym).

Kwantyle

•Kwantyle definiuje się jako wartości cechy badanej populacji,

przedstawionej w postaci szeregu statystycznego, które dzielą

zbiorowość na określone części pod względem liczby jednostek.

Części te pozostają do siebie w określonych proporcjach.

•Kwartyl pierwszy

(Q

1

) dzieli zbiorowość na dwie części tak, że

25% jednostek zbiorowości ma wartości cechy niższe bądź równe

kwartylowi pierwszemu, a 75% równe bądź wyższe.

•Mediana

(Me, kwartyl drugi) dzieli zbiorowość na dwie równe

części; połowa jednostek ma wartości cechy mniejsze bądź równe

medianie, a połowa wartości cechy równe lub większe od Me. W

szeregu szczegółowym medianą jest wartość znajdująca się w

jego środku, stąd mediana jest nazywana wartością środkową.

•Kwartyl trzeci

(Q

3

) dzieli zbiorowość na dwie części tak, że 75%

jednostek zbiorowości ma wartości cechy niższe bądź równe

kwartylowi trzeciemu, a 25% równe bądź wyższe.

Mediana

• Medianę wyznacza się ze wzoru:



















)

(

2

1

1

2

2

2

1

n

n

n

x

x

x

Me

gdy n jest nieparzyste

gdy n jest parzyste (mediana jest średnią
dwu środkowych elementów szeregu)

Przykład:
Dane czasów hospitalizacji pacjentów:
6, 7, 8, 8, 9, 11, 11, 11, 14, 14, 15, 16, 117
Ponieważ szereg liczy 13 elementów, to zgodnie ze
wzorem, środkowym jest element (13+1)÷2=7 (siódmy)
w szeregu uporządkowanych wartości, czyli ten o
wartości11.
Łatwo udowodnić, że także mediana jest niewrażliwa na
przypadki odstające. Obok średniej arytmetycznej,
mediana jest najczęściej stosowanym parametrem
statystycznym.

Kwartyle

•Kwartyle wyznacza się w sposób analogiczny do

mediany. Wyznaczając medianę, dzielimy badany

szereg na dwie połowy. Wyznaczenie kwartyla

pierwszego sprowadza się do znalezienia mediany w

połowie zawierającej jednostki mniejsze od mediany, a

wyznaczenie kwartyla trzeciego to znalezienie

mediany w połowie zawierającej jednostki większe od

mediany.

•Opierając się na poprzednim przykładzie, kwartylem

pierwszym będzie mediana szeregu: 6, 7, 8, 8, 9, 11,

11, czyli 8, natomiast kwartylem trzecim będzie

mediana szeregu 11, 11, 14, 14, 15, 16, 117, czyli 14.

•Podsumowując, dla przytoczonego przykładu:
•Q

1

=8, Me=11, Q

1

=14

Centyle

•Centyle stosowane są dla prób o dużej

liczebności. Wskazują jaki procent jednostek w

próbie uzyskał wynik mniejszy od danego. Tym

samym centyl 50 odpowiada medianie, a centyle

25 i 75 to odpowiednio pierwszy i trzeci kwartyl.
•Centyle są często stosowane do odnoszenie

różnych pomiarów antropometrycznych u

badanego dziecka do ogółu populacji dzieci.

Służą do tego siatki centylowe. Są to wykresy

kilku wybranych centyli (zwykle 3, 10, 25, 50, 75,

90 i 97) w zależności od wieku dla wybranego

parametru antropometrycznego (np. wagi,

wzrostu, obwodu głowy, itp.).

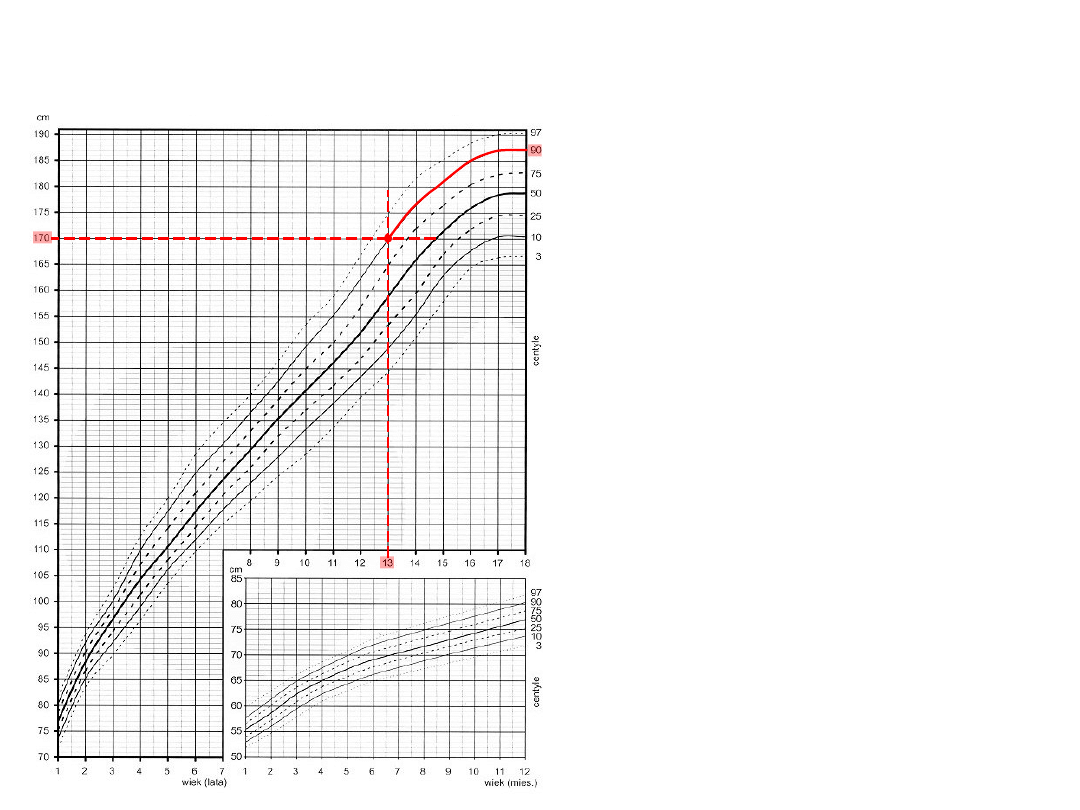
Centyle

Siatka centylowa wzrostu u
chłopców

Przykład:
Ocenić wzrost 13 letniego
chłopca, mierzącego 170 cm.

Ponieważ dla populacji 13-letnich
chłopców, wzrost 170 cm jest 90-
tym centylem, zatem w tej
grupie wiekowej 90% chłopców
jest niższych niż 170 cm, a 10%
ma wzrost wyższy od 170 cm.