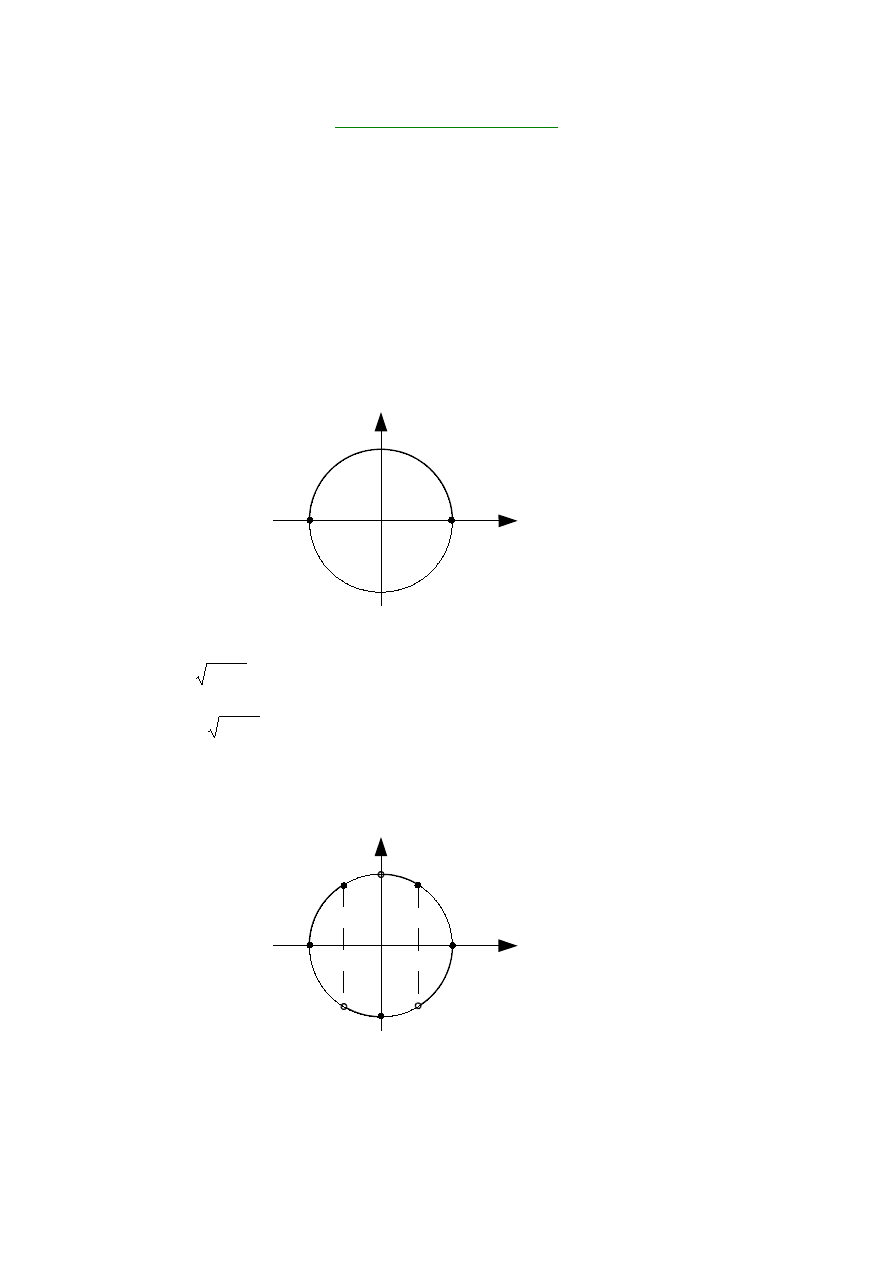
FUNKCJE UWIKŁANE
Niech
R
R
2
:
F
Rozważamy równanie
0
,
y
x
F
.
Definicja
Jeśli istnieje funkcja
x
f
y
, spełniająca w każdym punkcie
R
X
x
warunek
0
)
(
,
x
f
x
F
, to nazywamy ją
funkcją uwikłaną
określoną w zbiorze X równaniem
0
,
y
x
F
.
Przykład
Rozważmy równanie
0
1
2
2
y
x
.
1
1
x
y
y = y
1
Istnieją funkcje uwikłane spełniające to równanie:
2
1
1 x
y
dla
1
,
1
x
lub
2
2
1 x
y
dla
1
,
1
x
.
Istnieje nieskończenie wiele funkcji uwikłanych spełniających powyższe równanie, na
przykład funkcja
3
y
y
.
1
1
x
y
y = y
3
Uwaga
Będziemy rozważać tylko ciągłe funkcje uwikłane.
1
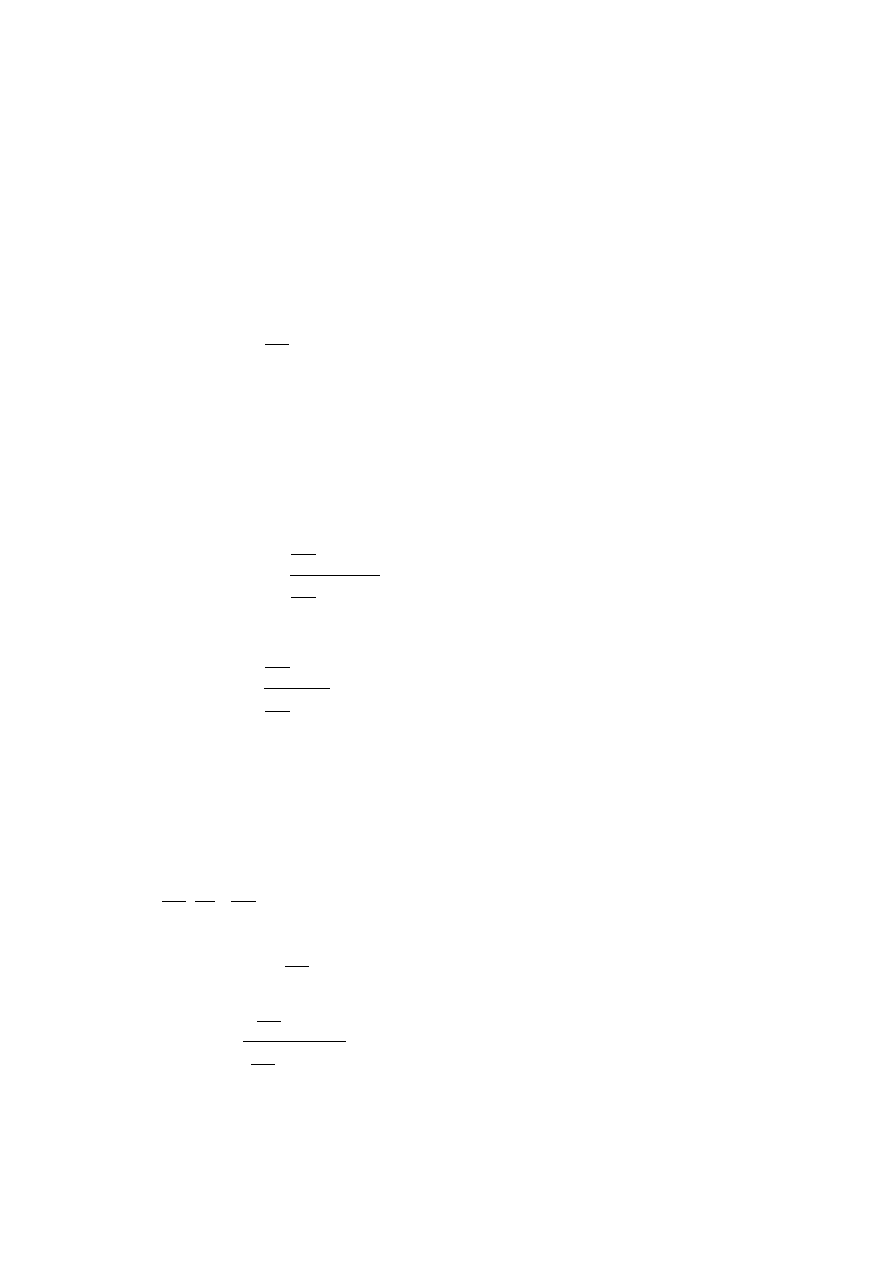
Rozważamy problem istnienia funkcji uwikłanej.
Np. równanie
0
1
2
2
y
x
nie określa żadnej funkcji uwikłanej,
natomiast równanie
0
2
x
y
określa dokładnie jedną funkcję uwikłaną.
Twierdzenie
(
o istnieniu i jednoznaczności funkcji uwikłanej
)
Z:
0
,
0
,
,
:
Top
0
0
0
0
0
0
0
1
2
y
x
y
F
y
x
F
U
y
x
P
U
C
F
U
F
U
R
R
T: !
ciągła funkcja uwikłana
x
f
y
określona w pewnym przedziale
0
0
, x
x
za pomocą równania
0
,
y
x
F
i spełniająca warunek
0
0
y
x
f
(czyli funkcja uwikłana przechodząca przez wybrany punkt P
0
).
Wniosek
Jeśli spełnione są założenia twierdzenia o istnieniu i jednoznaczności funkcji uwikłanej, to
x
f '
w pewnym otoczeniu punktu x
0
i
)
(
,
)
(
,
'
x
f
x
y
F
x
f
x
x
F
x
f
lub krótko:
y
x
y
F
y
x
x
F
y
,
,
'
.
Dowód
(szkic)
Rozważmy równanie
0
,
y
x
F
. Z twierdzenia o istnieniu i jednoznaczności funkcji
uwikłanej wiemy, że funkcja uwikłana
)
(x
f
y
taka, że
0
0
,
dla
0
)
(
,
x
x
x
x
f
x
F
.
Równanie różniczkujemy stronami i wyznaczamy pochodną funkcji f.
)
(
,
)
(
,
)
(
'
0
,
dla
0
)
(
'
0
0
1
x
f
x
y
F
x
f
x
x
F
x
f
y
F
x
x
x
x
f
y
F
x
x
x
F
ڤ
2
Uwaga
Korzystając z powyższego wniosku możemy wyznaczyć ekstrema funkcji bez rozwikłania tej
funkcji.
Twierdzenie
(
o drugiej pochodnej funkcji uwikłanej
)
Z:
0
,
0
,
,
:
Top
0
0
0
0
0
0
0
2
2
y
x
y
F
y
x
F
U
y
x
P
U
C
F
U
F
U
R
R
T: Funkcja ciągła
x
f
y
określona w przedziale
0
0
, x
x
równaniem
0
,
y
x
F
i
spełniająca warunek
0
0
y
x
f
posiada w pewnym otoczeniu punktu x
0
drugą pochodną.
Wzór na drugą pochodną funkcji uwikłanej
Na podstawie wniosku o pierwszej pochodnej funkcji uwikłanej
0
gdzie
,
,
,
'
y
F
y
x
y
F
y
x
x
F
y
.
Stąd
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
2
2
'
1
'
''
y
F
y
F
x
F
y
F
x
F
y
x
F
y
F
x
F
y
F
y
F
x
F
y
F
x
F
y
x
F
x
F
x
y
F
y
F
x
F
y
F
x
F
y
y
F
y
x
F
y
F
y
x
y
F
x
x
x
F
y
bo, na podstawie założeń o ciągłości drugiej pochodnej funkcji F, mieszane pochodne
cząstkowe są sobie równe.
3
Wniosek
Jeśli spełnione są założenia powyższego twierdzenia i dodatkowo jeśli
0
)
(
'
0
x
y
, to
0
,
0
0
y
x
x
F
, a stąd
0
0
0
0
2
2
0
,
,
)
(
''
y
x
y
F
y
x
x
F
x
y
.
Korzystając z powyższego wniosku można łatwo zbadać
ekstrema lokalne funkcji uwikłanej
f(x)
y
.
Pierwsza pochodna funkcji f musi być równa 0, czyli
0
0
y
F
x
F
Stąd wyznaczamy punkty stacjonarne funkcji F, a następnie wystarczy zbadać w każdym z
punktów stacjonarnych
)
,
(
0
0
y
x
P
wartość ilorazu
y
F
x
F
2
2
.
Wtedy, jeśli
0
)
,
(
)
,
(
0
0
0
0
2
2
y
x
y
F
y
x
x
F
, to funkcja uwikłana ma w punkcie
)
,
(
0
0
y
x
P
maksimum
lokalne. Analogicznie, jeżeli iloraz ten jest mniejszy od 0, to funkcja uwikłana ma w punkcie
)
,
(
0
0
y
x
P
minimum lokalne.
Przykład
(bez twierdzenia)
Niech
0
,
,
z
y
x
F
, gdzie
)
,
( y
x
z
z
.
Aby wyznaczyć pochodne cząstkowe funkcji
)
,
( y
x
z
z
różniczkujemy równanie
0
,
,
z
y
x
F
kolejno względem zmiennej x i y (x, y – zmienne niezależne)
z
F
y
F
y
z
z
F
x
F
x
z
y
z
z
F
y
F
x
F
x
z
z
F
y
F
x
F
0
1
0
0
0
1
dla
0
z
F
.
opracował Mateusz Targosz
4