Fizyka przepływów.

Elementy biofizyki układu kr

ąż

enia

Jakub Zieli

ń

ski

Zakład Biofizyki i Fizjologii Człowieka

Ci

ś

nienie i prawo Pascala

Ci

ś

nienie to wielko

ść

skalarna okre

ś

lona jako warto

ść

siły działaj

ą

cej

prostopadle do powierzchni podzielona przez powierzchni

ę

na jak

ą

ona działa:

F = p * s

Jednostk

ą

jest Pascal [Pa] = [N/m

2

].

Prawo Pascala (stało

ść

ci

ś

nienia).

Zastosowania prawa Pascala:
strzykawka, prasy hydrauliczne.

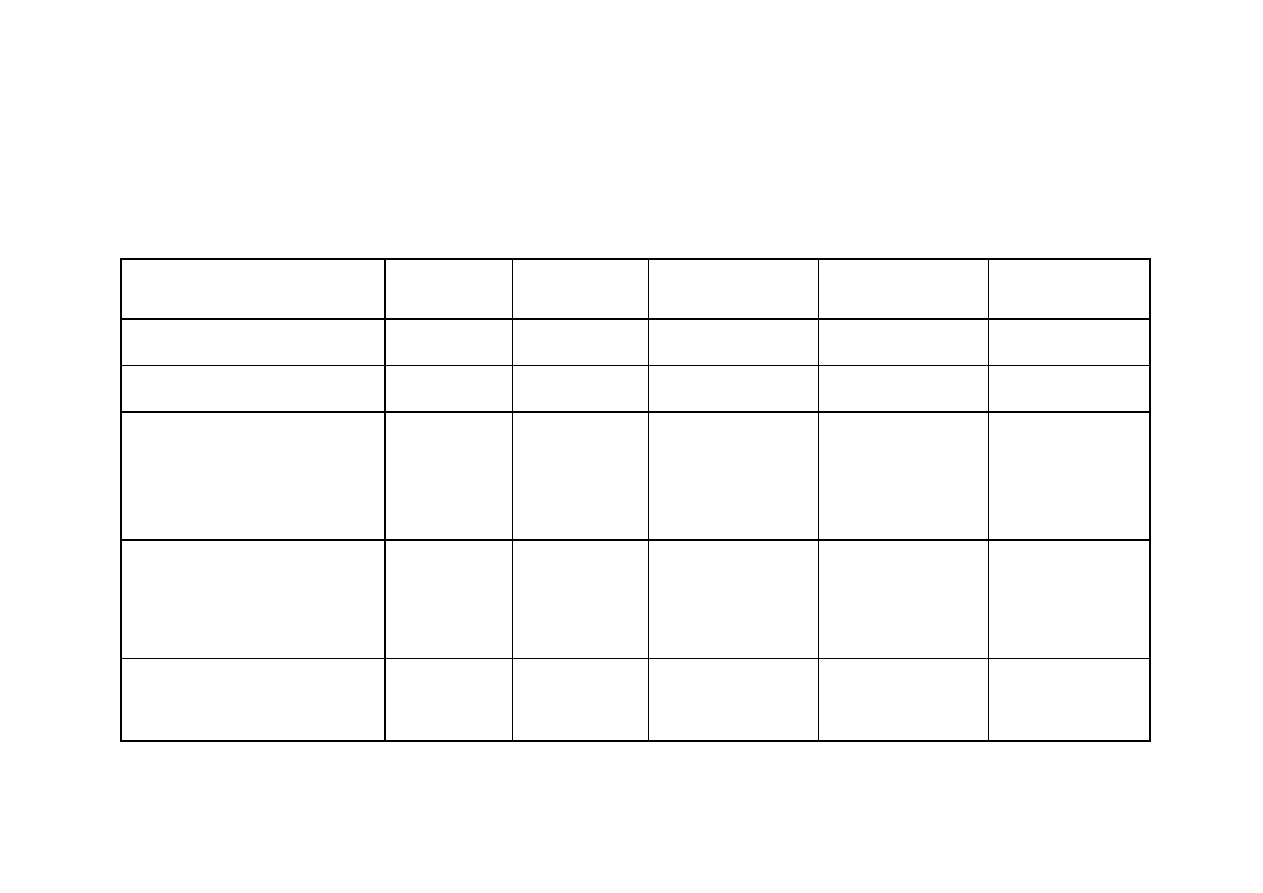
Przeliczanie jednostek

133

101325

98100

10

5

1

Pa

1

0,00132

0,00132

0,00133

1 tor [Tr] =
1 mmHg

760

1

1,033

1,013

1 atmosfera
fizyczna [atm] =
760 mmHg

736

0,968

1

0,981

1 atmosfera
techniczna [at] =
1 kG/cm

2

750

0,987

1,02

1

1 bar

0,0075

0,987×10

-5

0,102×10

-4

10

-5

1 Pa [N/m

2

]

mmHg

atm

at

bar

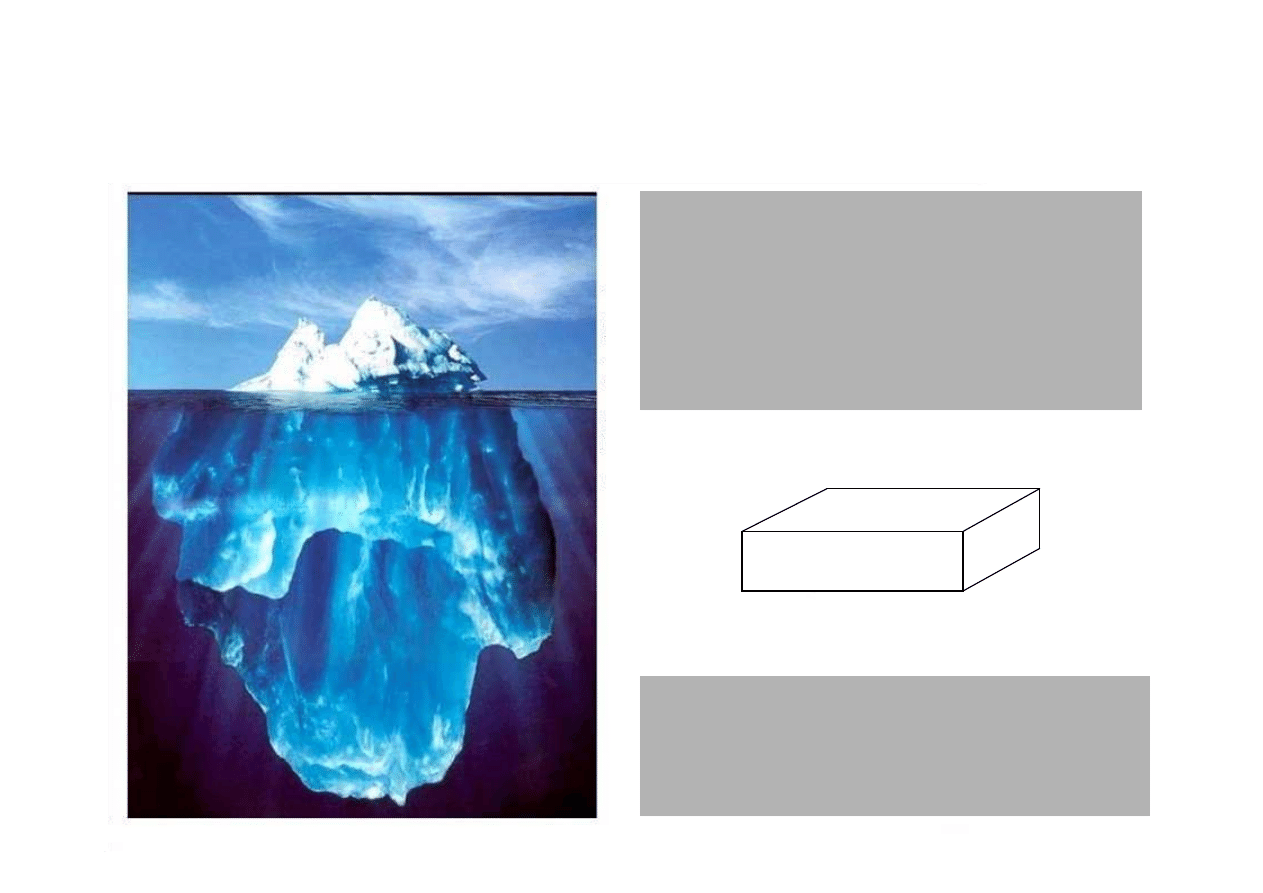
Ci

ś

nienie hydrostatyczne

i Prawo Archimedesa

Prawo Pascala „z grawitacj

ą

”

p = p

0

–

ρ

ρ

ρ

ρ

g h

h

p

2

= p

1

+

ρ

g h

p

1

s

F

w

= F

2

– F

1

= (p

2

– p

1

)*s

=

ρ

g h s =

ρ

g V

Zagadka

Dlaczego nie działa

nast

ę

puj

ą

ce

perpetuum mobile?

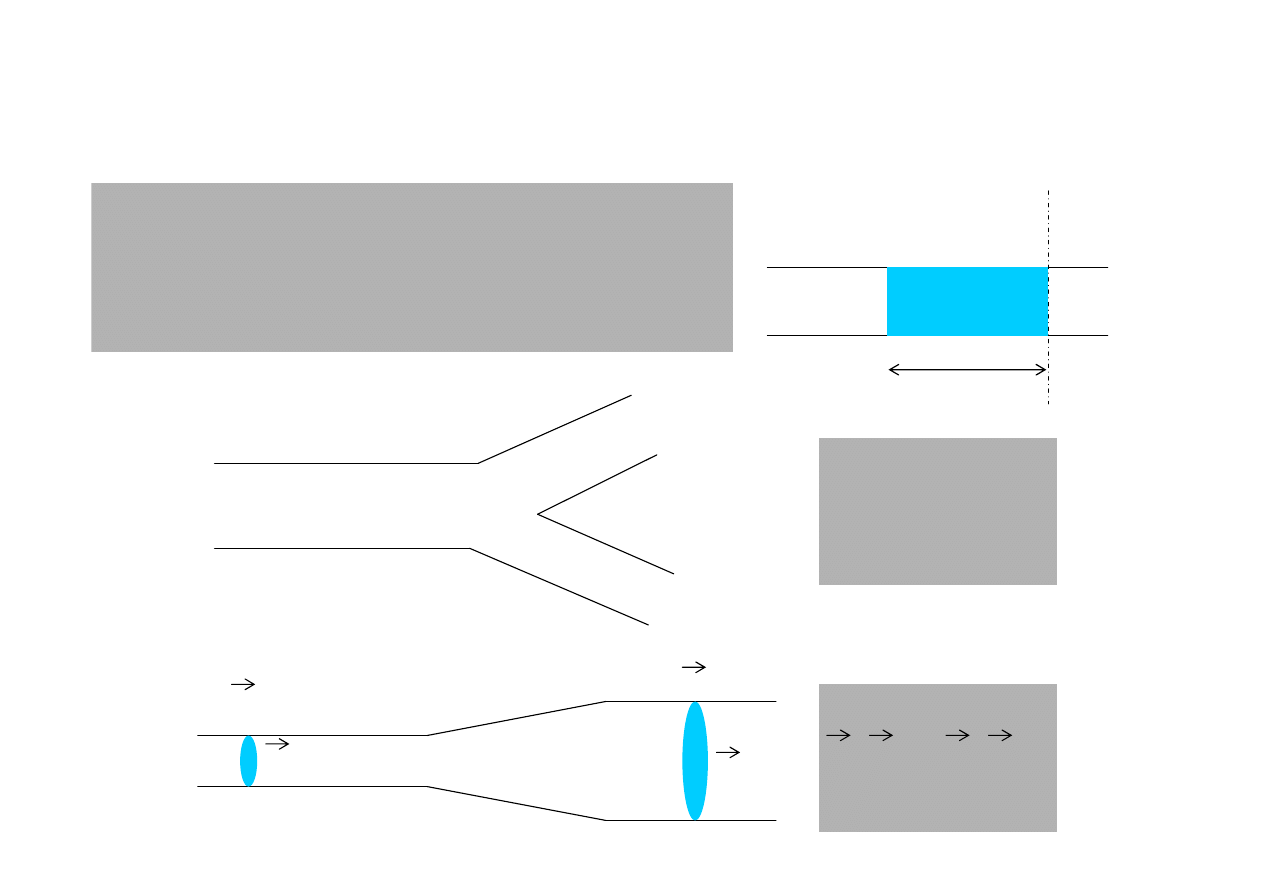
Prawo ci

ą

gło

ś

ci strumienia

Q

1

Q

2

Q

3

Q

1

= Q

2

+ Q

3

s

1

s

2

v

1

v

2

v

1

*s

1

= v

2

*s

2

Strumie

ń

– obj

ę

to

ść

przepływaj

ą

ca,

przez zadan

ą

powierzchni

ę

w jednostce czasu

Q = V/t = v*t*s/t = v*s

V = x*s = v*t*s

s

x

Równanie Bernoulliego

p +

ρ

ρ

ρ

ρ

g h + ½

ρ

ρ

ρ

ρ

v

2

= const

p – ci

ś

nienie statyczne

ρρρρ

g h – ci

ś

nienie hydrostatyczne

½

ρρρρ

v

2

– ci

ś

nienie dynamiczne

Prawo Bernoulliego to przejaw zasady
zachowania energii mechanicznej dla płynu.

Prawo to NIE uwzgl

ę

dnia spadku ci

ś

nienia

spowodowanego oporem naczy

ń

!

Kierunek przepływu

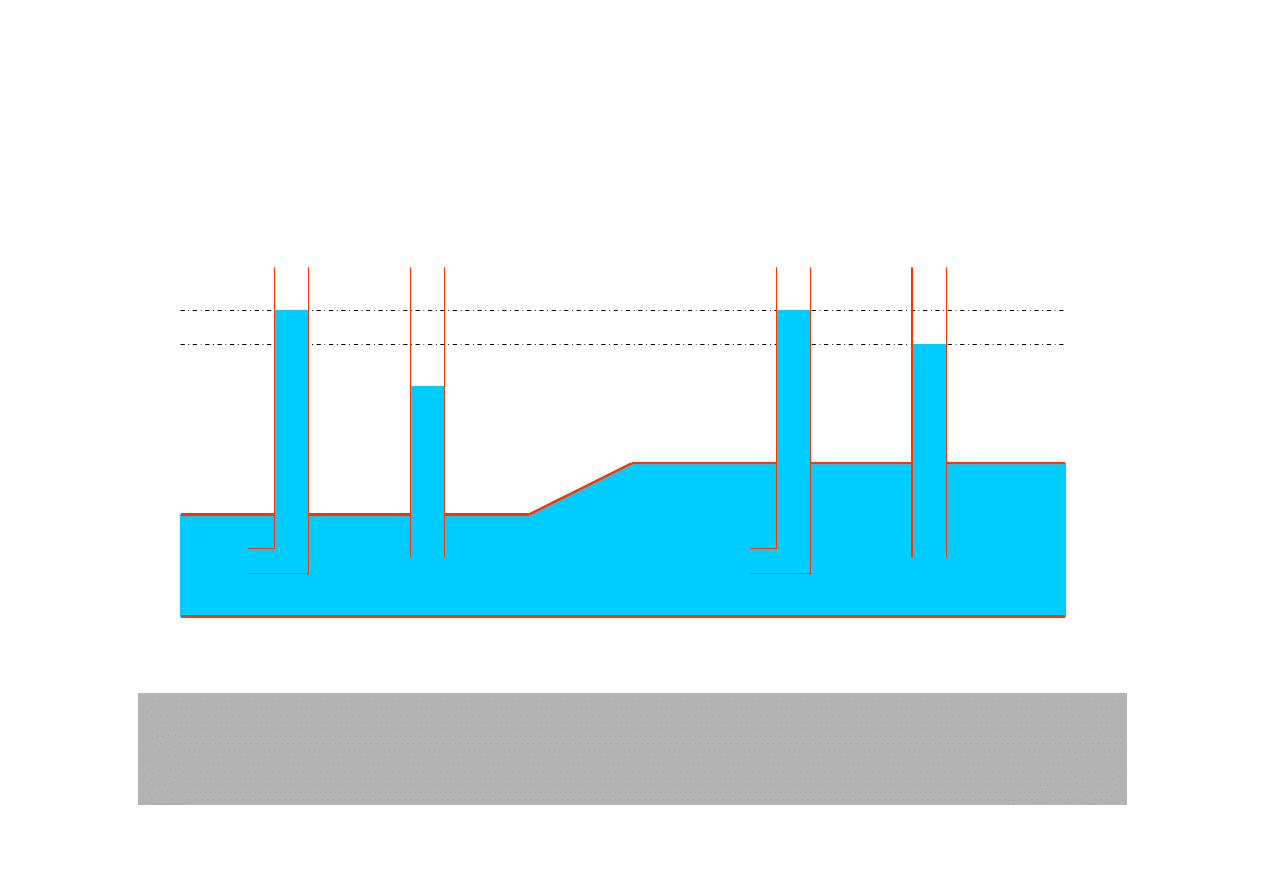
Pomiar tzw. ci

ś

nienia całkowitego

i ci

ś

nienia statycznego

Uwaga, ci

ś

nienie dynamiczne nie powoduje nacisku na

ś

cianki naczynia

!

Paradoks hydrodynamiczny

W miejscu przew

ęż

enia naczynia ci

ś

nienie wywierane przez

poruszaj

ą

cy si

ę

płyn na

ś

cianki naczynia jest zmniejszone

Zastosowania:
• siła no

ś

na skrzydła samolotu

•

ż

eglowanie przy bocznym wietrze

• zw

ęż

ka Venturiego

Problemy:
• powstanie t

ę

tniaka powoduje lokalny wzrost ci

ś

nienia krwi

• spadek ci

ś

nienia w zw

ęż

eniu zwi

ę

ksza ryzyko „zapadni

ę

cia” si

ę

naczynia

• osiadanie statków w płytkim akwenie
• zrywanie spadzistych dachów podczas wichury

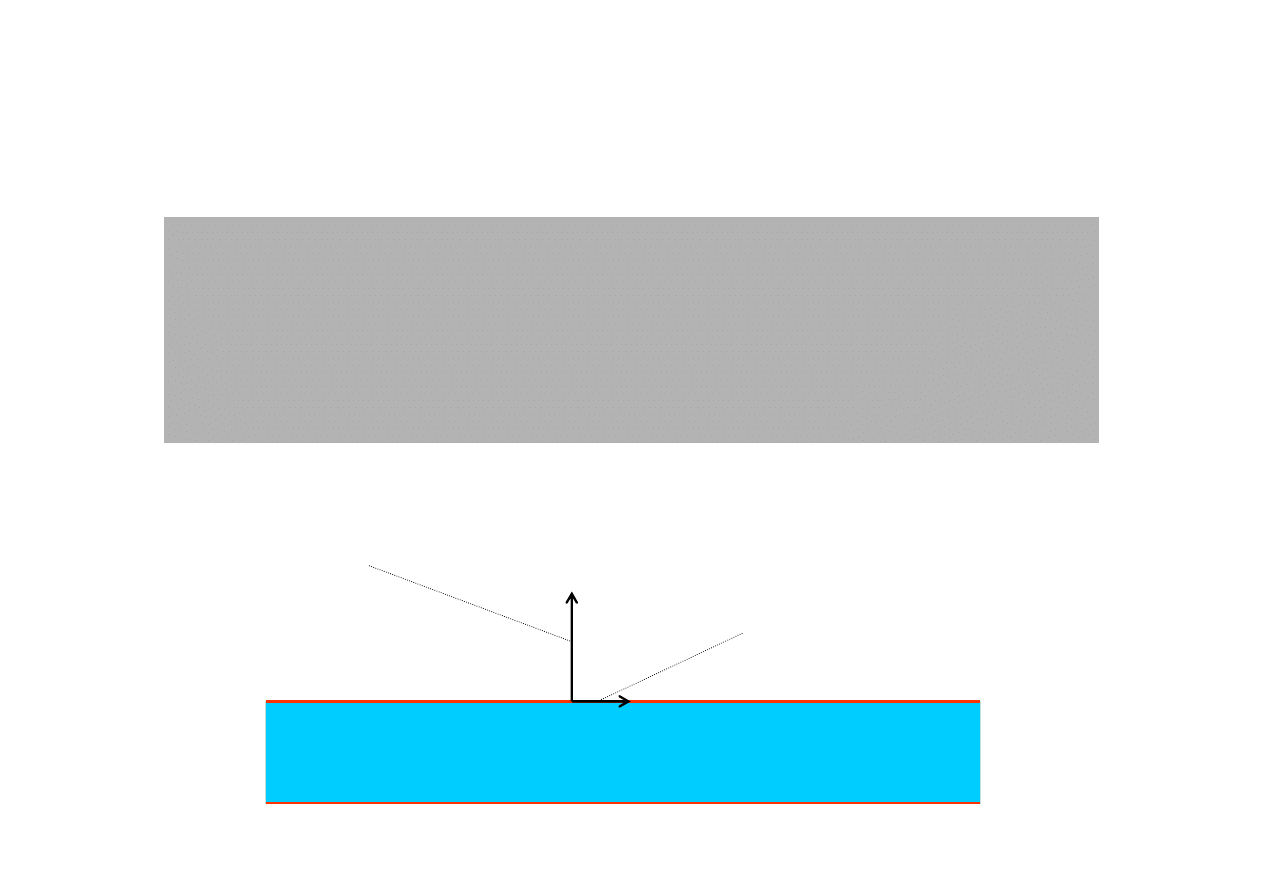
Ci

ś

nienie vs. napr

ęż

enie

ś

cinaj

ą

ce

Ci

ś

nienie to g

ę

sto

ść

powierzchniowa siły prostopadłej

do powierzchni.

Napr

ęż

enie

ś

cinaj

ą

ce to g

ę

sto

ść

powierzchniowa siły

równoległej do powierzchni

Siła wywołana przez ci

ś

nienie

Siła wywołana przez
napr

ęż

enie

ś

cinaj

ą

ce

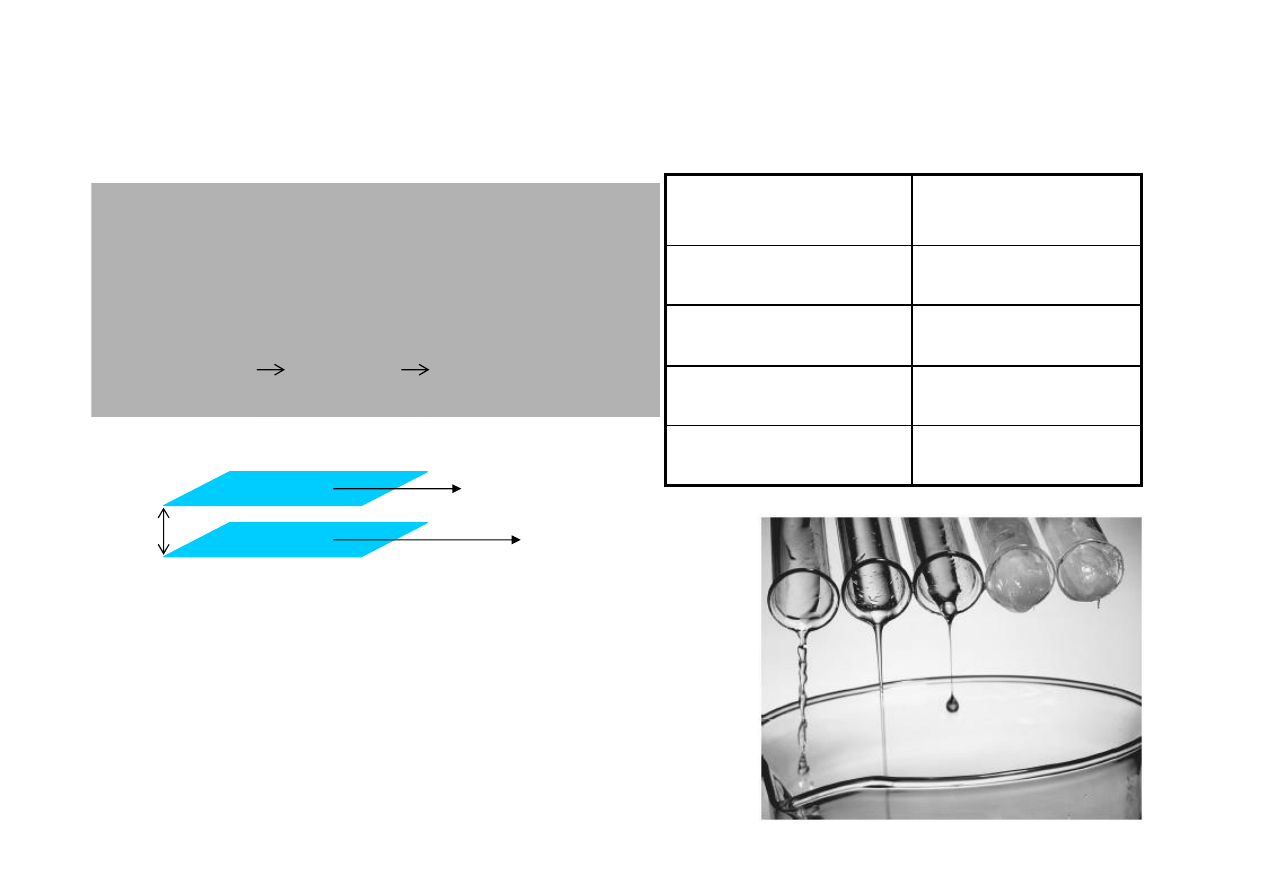
Lepko

ść

(tarcie wewn

ę

trzne)

3 - 5 × 10

-3

Krew

1.9 - 2.3 × 10

-3

Osocze

1.003 × 10

−3

Woda (20

o

C)

17.4 × 10

−6

Powietrze (0

o

C)

Lepko

ść

[Pa*s]

Substancja

Lepko

ść

dynamiczna okre

ś

la sił

ę

z jak

ą

jedna warstwa płynu działa na drug

ą

,

równoległ

ą

do niej lecz poruszaj

ą

c

ą

si

ę

z inn

ą

pr

ę

dko

ś

ci

ą

:

F =

µµµµ

s

∆

v/

∆

x

s

v

1

v

2

∆

x

Jednostk

ą

lepko

ś

ci dynamicznej jest [Pa*s].

Lepko

ś

ci nie nale

ż

y myli

ć

z g

ę

sto

ś

ci

ą

– galaretka

„g

ę

stniej

ą

c” zwi

ę

ksza lepko

ść

, a nie g

ę

sto

ść

!

Lepko

ść

kinematyczna

ν

=

µ

/

ρ

[m

2

/s]

.

Rodzaje przepływów cieczy

Liczba Reynoldsa

Re = d v

ρ

ρ

ρ

ρ

/

µ =

µ =

µ =

µ =

d v /

νννν

d – wymiar charakterystyczny,
np.

ś

rednica naczynia

Re < 2300 – przepływ laminarny

2300 < Re < 4000 – przej

ś

ciowy

Re > 4000 – przepływ turbulentny

Przepływ laminarny mo

ż

e by

ć

stacjonarny (ustalony) lub nie.
Turbulencje nigdy nie s

ą

stacjonarne.

Opór naczy

ń

Opór naczynia to iloraz spadku ci

ś

nienia przez strumie

ń

przepływaj

ą

cej cieczy:

R =

∆∆∆∆

p/Q

Jest to hydrodynamiczny odpowiednik prawa Ohma: spadek ci

ś

nienia

odpowiada spadkowi napi

ę

cia, a strumie

ń

cieczy nat

ęż

eniu pr

ą

du

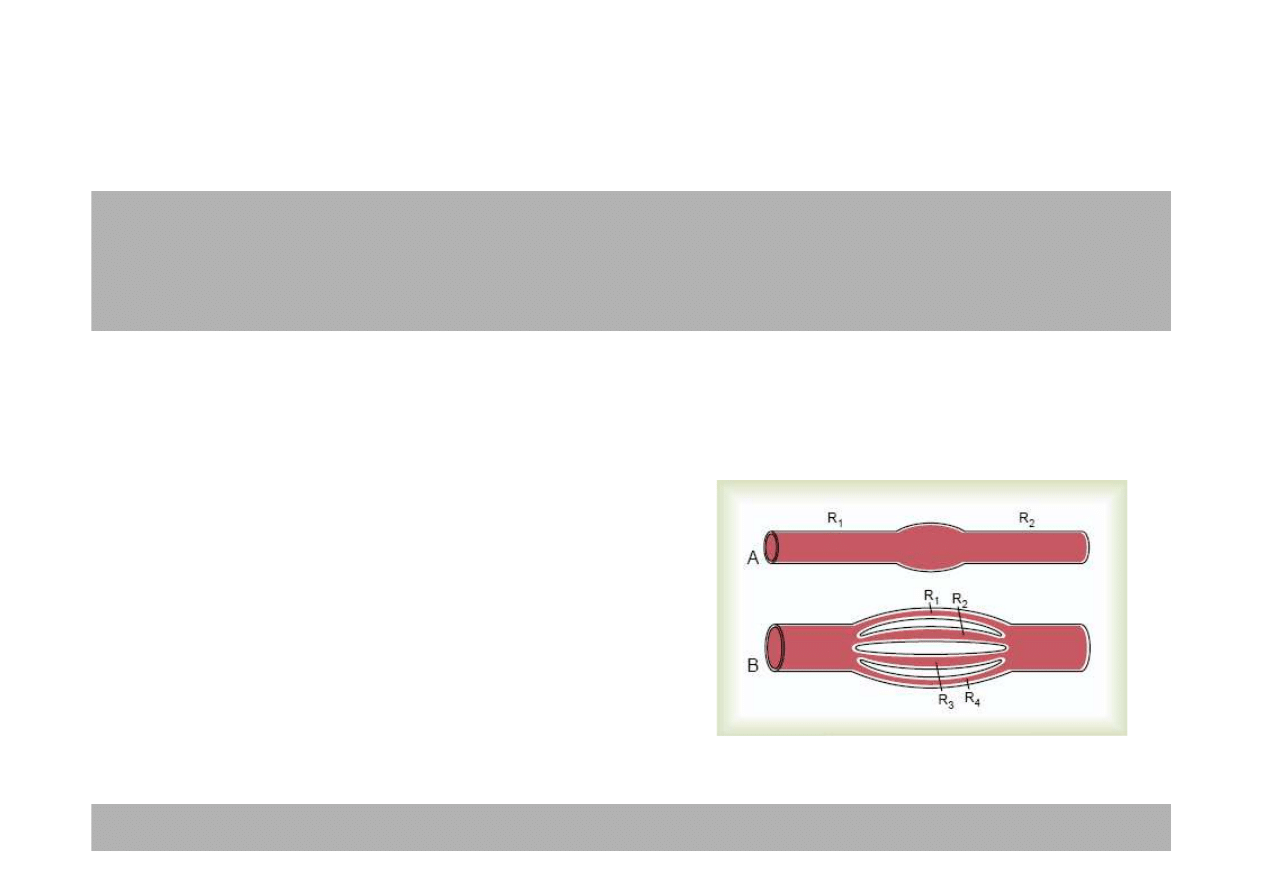
Opory naczy

ń

poł

ą

czonych szeregowo

dodaj

ą

si

ę

: R = R

1

+ R

2

Dla naczy

ń

poł

ą

czonych równolegle, dodaj

ą

si

ę

odwrotno

ś

ci oporów: 1/R = 1/R

1

+ 1/R

2

.

Opór całkowity jest wi

ę

c mniejszy od oporów

pojedynczych naczy

ń

Pozostaje jednak pytanie: ile wynosi opór pojedynczego naczynia?

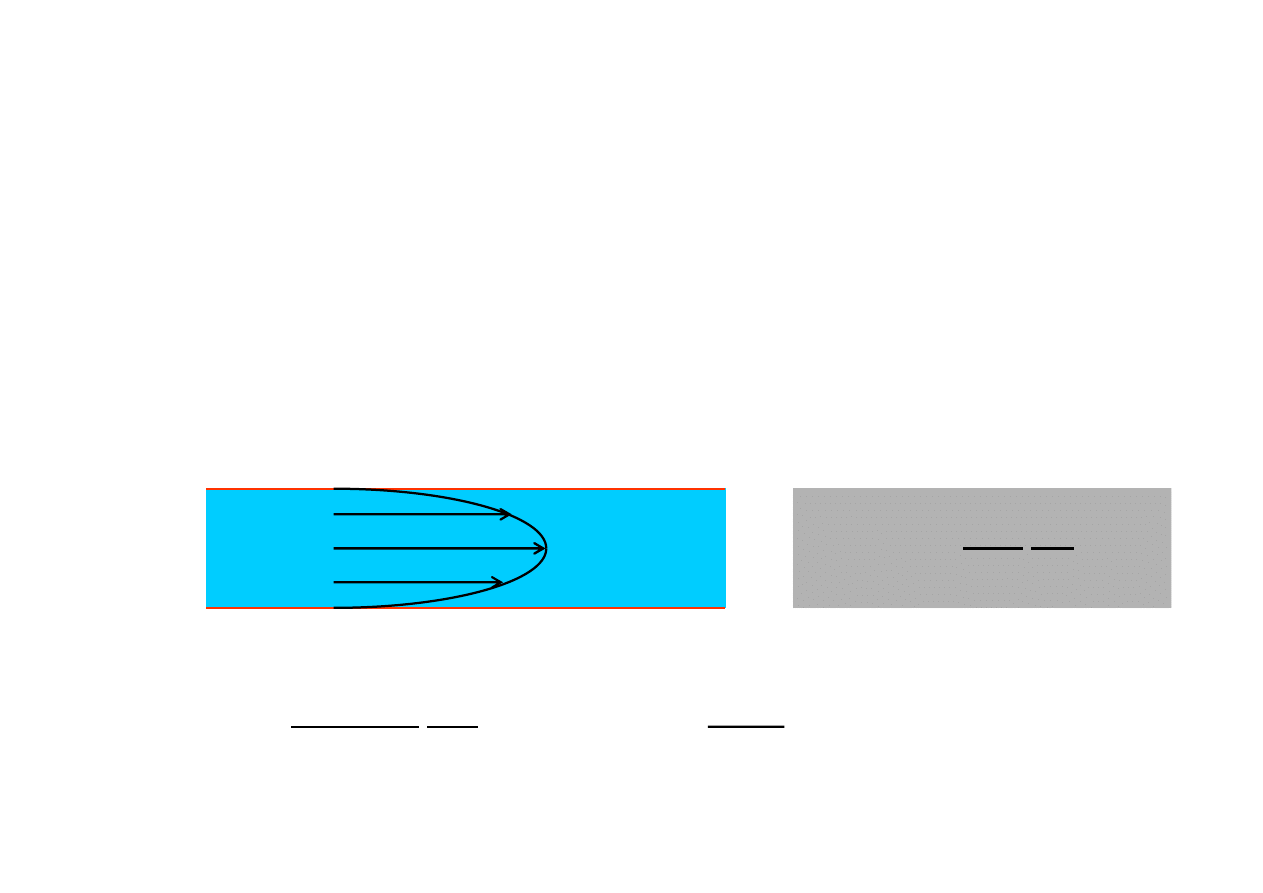
Prawo Hagena – Poiseuille’a

Zało

ż

enia:

• niesko

ń

czona rura o przekroju kołowym

•

ś

cianki idealnie sztywne

• przepływ ustalony
• ciecz Newtonowska (stało

ść

lepko

ś

ci)

π

R

4

∆

p

8

µ

L

Q =

(R

2

– r

2

)

∆

p

4

µ

L

v =

2

π

R

2

v

max

=

Q

v

ś

r

= ½ v

max

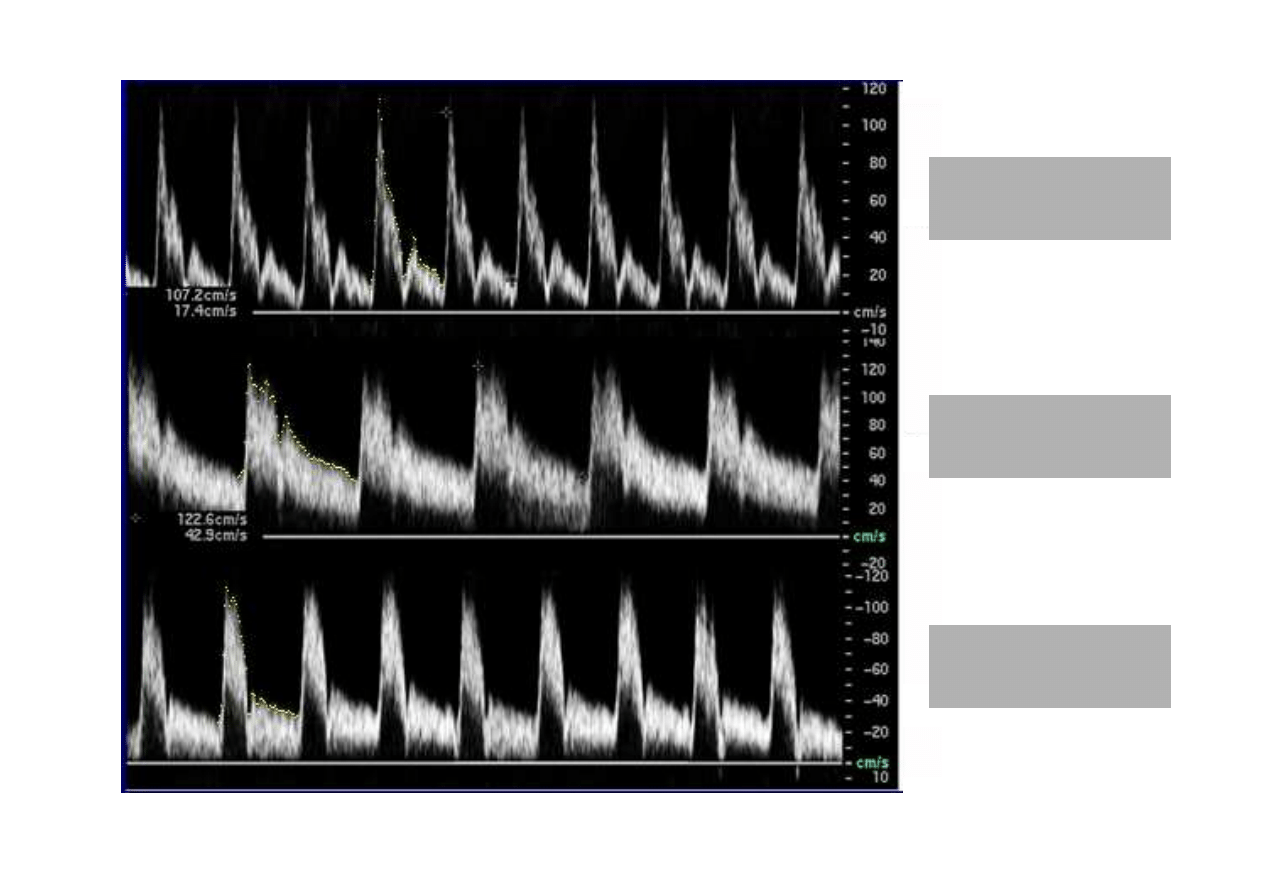
T

ę

tnica szyjna

zewn

ę

trzna

T

ę

tnica szyjna

wewn

ę

trzna

T

ę

tnica szyjna

wspólna

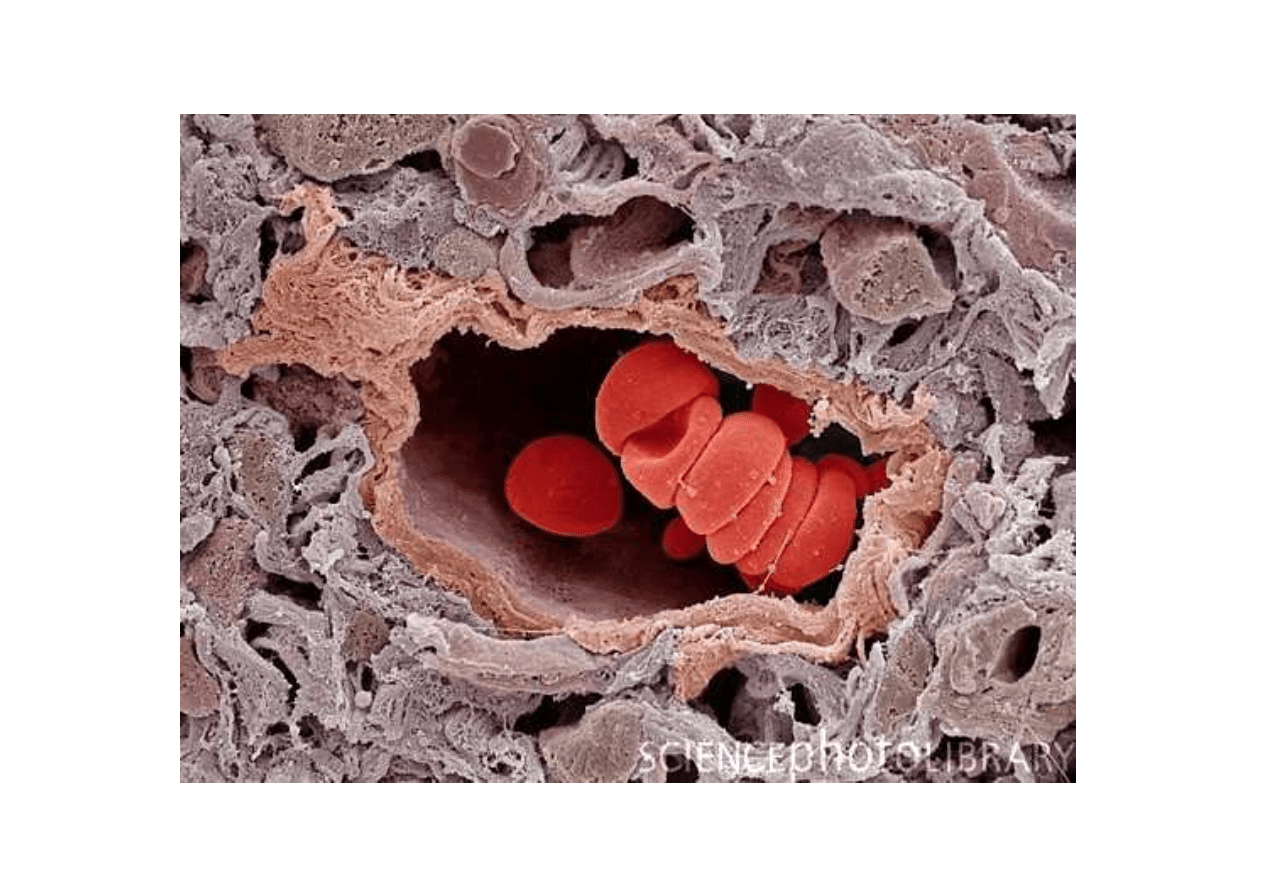
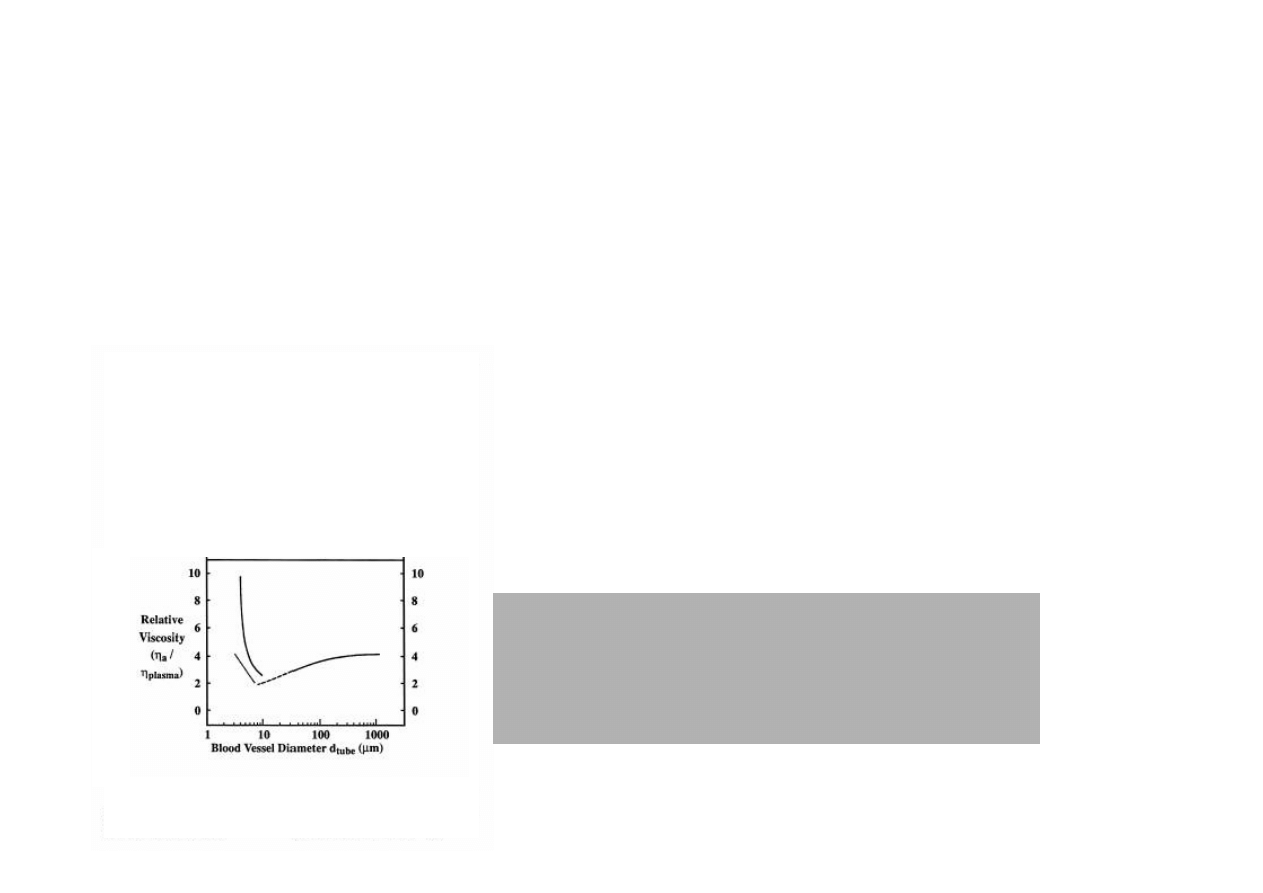
Zmiany lepko

ś

ci krwi

Odkształcanie erytrocytów –
spadek lepko

ś

ci dla du

ż

ych napr

ęż

e

ń ś

cinaj

ą

cych

Agregacja erytrocytów – wzrost lepko

ś

ci przy

ś

ciankach naczynia

Spadek lepko

ś

ci dla naczy

ń

o

ś

rednicy poni

ż

ej 100 mikronów

Wzrost lepko

ś

ci gdy

ś

rednica naczynia mniejsza ni

ż

10 mikronów –

krew nie mo

ż

e by

ć

ju

ż

traktowana jako o

ś

rodek ci

ą

gły. Lepko

ść

to suma

lepko

ś

ci osocza i tarcia erytrocytów o

ś

cianki naczy

ń

Lepko

ść

gwałtownie ro

ś

nie wraz

ze wzrostem hematoktytu

Prawo Hagena – Poiseuille’a

Zało

ż

enia:

• niesko

ń

czona rura o przekroju kołowym

•

ś

cianki idealnie sztywne

• przepływ ustalony
• ciecz Newtonowska (stało

ść

lepko

ś

ci)

π

R

4

∆

p

8

µ

L

Q =

ś

adne z zało

ż

e

ń

prawa Hagena–Poiseuille’a nie jest spełnione

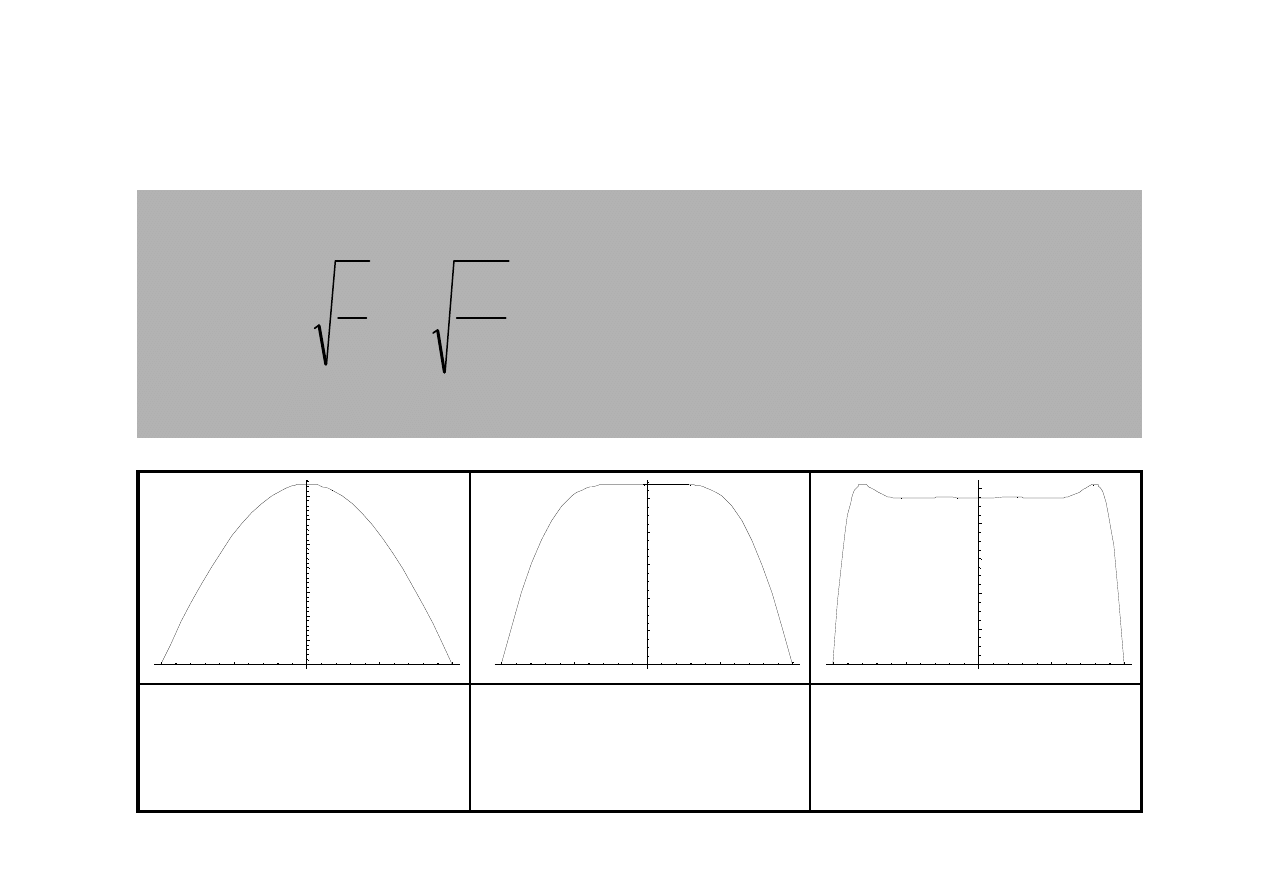
-1

-0.5

0.5

1

0.02

0.04

0.06

0.08

0.1

Liczba Womersleya

r = 1 cm

ω

= 10 Hz

α

= 16,24

r = 1 cm

ω

= 1 Hz

α

= 5,14

r = 1 mm

ω

= 1 Hz

α

= 0,51

-1

-0.5

0.5

1

0.2

0.4

0.6

0.8

1

-1

-0.5

0.5

1

0.001

0.002

0.003

0.004

0.005

0.006

0.007

µ

ωρ

υ

ω

α

R

R

=

=

R – promie

ń

naczynia

ω

– cz

ę

sto

ść

t

ę

tna

ρ

– g

ę

sto

ść

krwi

µ

– lepko

ść

dynamiczna

ν

– lepko

ść

kinematyczna

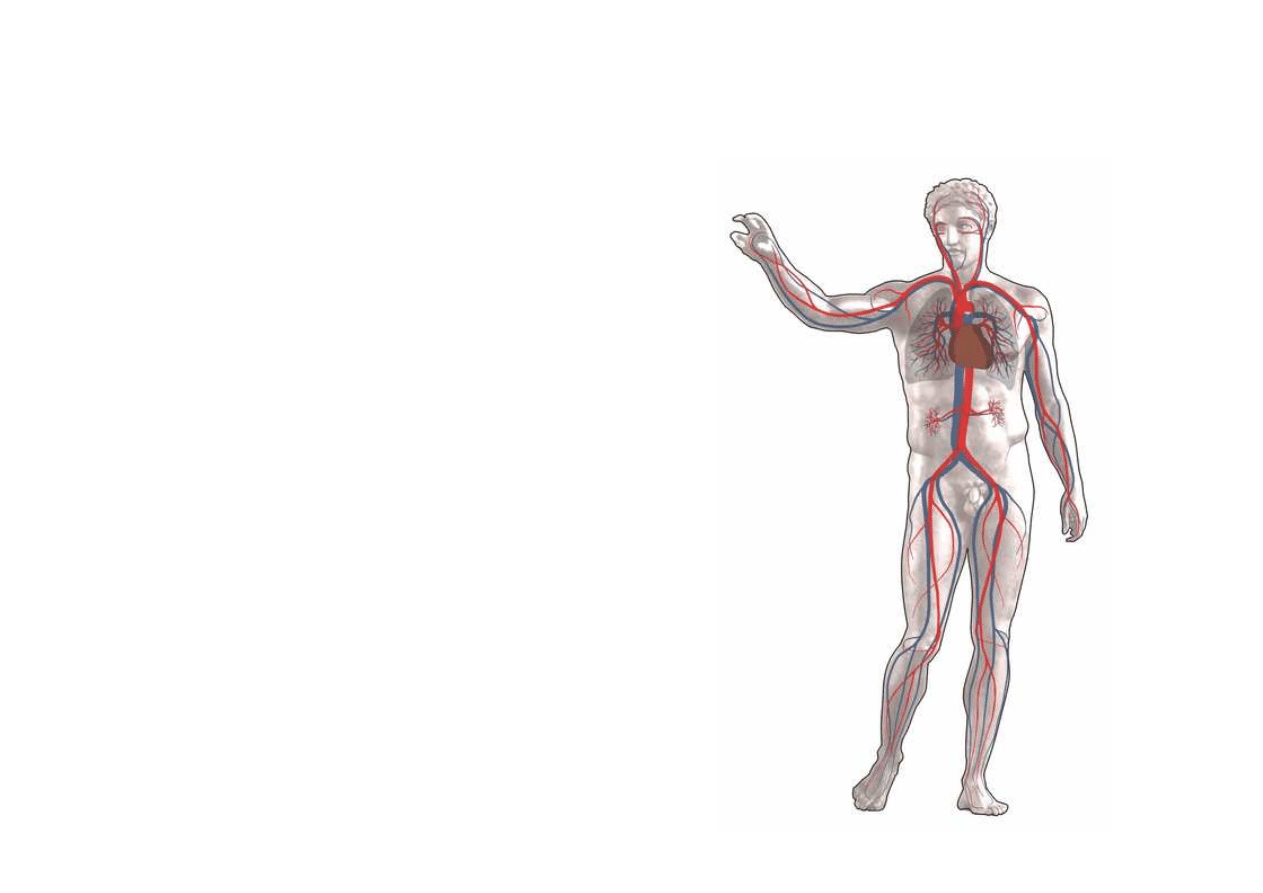
Układ krwiono

ś

ny człowieka

Układ krwiono

ś

ny:

• doprowadza tlen i odprowadza CO

2

• dostarcza substancje od

ż

ywcze

i odprowadza „odpady”

• rozprowadza ciepło (termoregulacja)
• transportuje hormony (no

ś

niki informacji)

• transportuje enzymy (katalizatory)
• transportuje przeciwciała

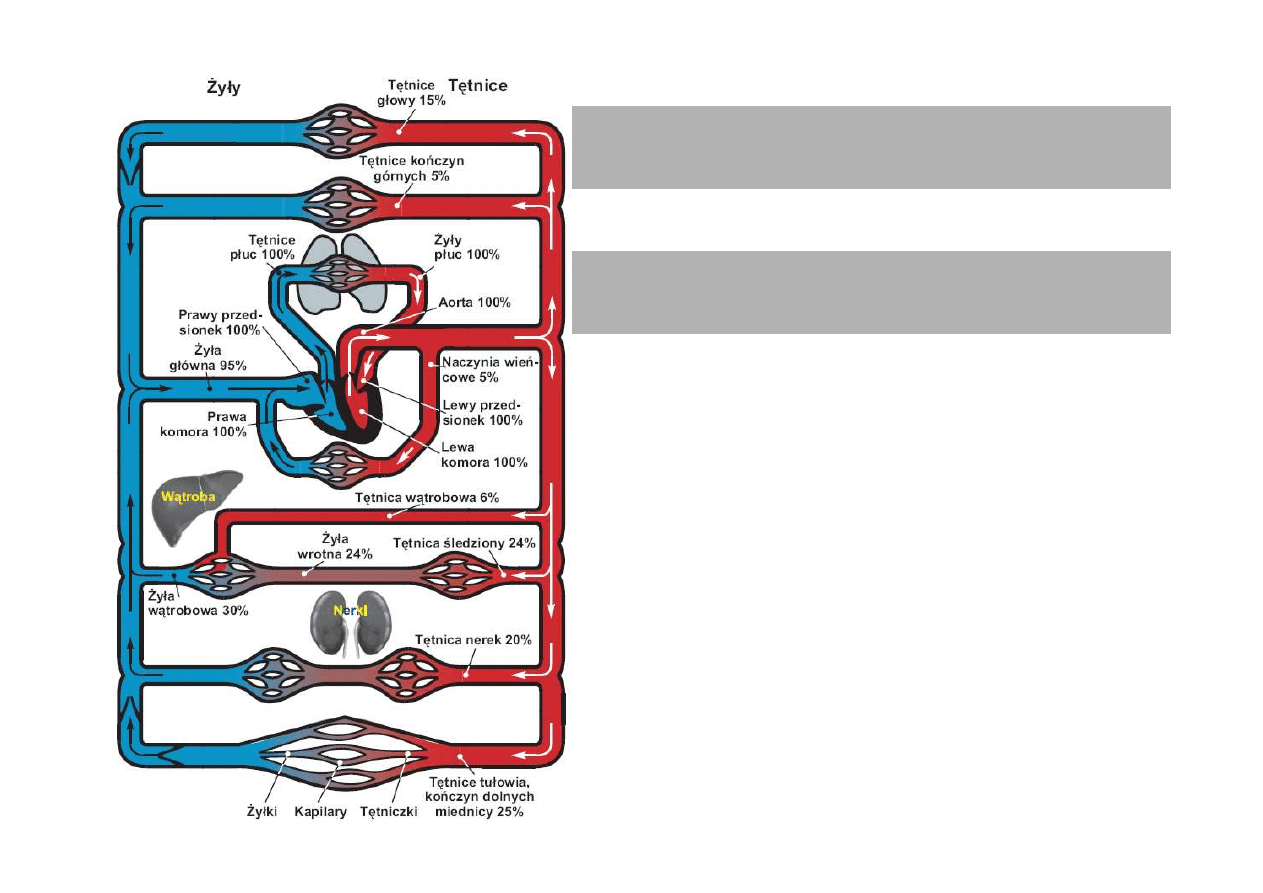
Ruch krwi wywoływany jest przez ró

ż

nic

ę

ci

ś

nie

ń

mi

ę

dzy układem t

ę

tniczym i

ż

ylnym

Typowo w kr

ąż

eniu płucnym i systemowym

w ci

ą

gu sekundy przepływa 88 ml krwi

Normalne ci

ś

nienie w aorcie: 120/80mmHg

(

ś

rednie 100mmHg)

Ci

ś

nienie w

ż

yle głównej: około 10mmHg

Normalne ci

ś

nienie w t

ę

tnicy płucnej:

22/8mmHg (

ś

rednie 15mmHg)

Ci

ś

nienie w

ż

yle płucnej: około 7mmHg

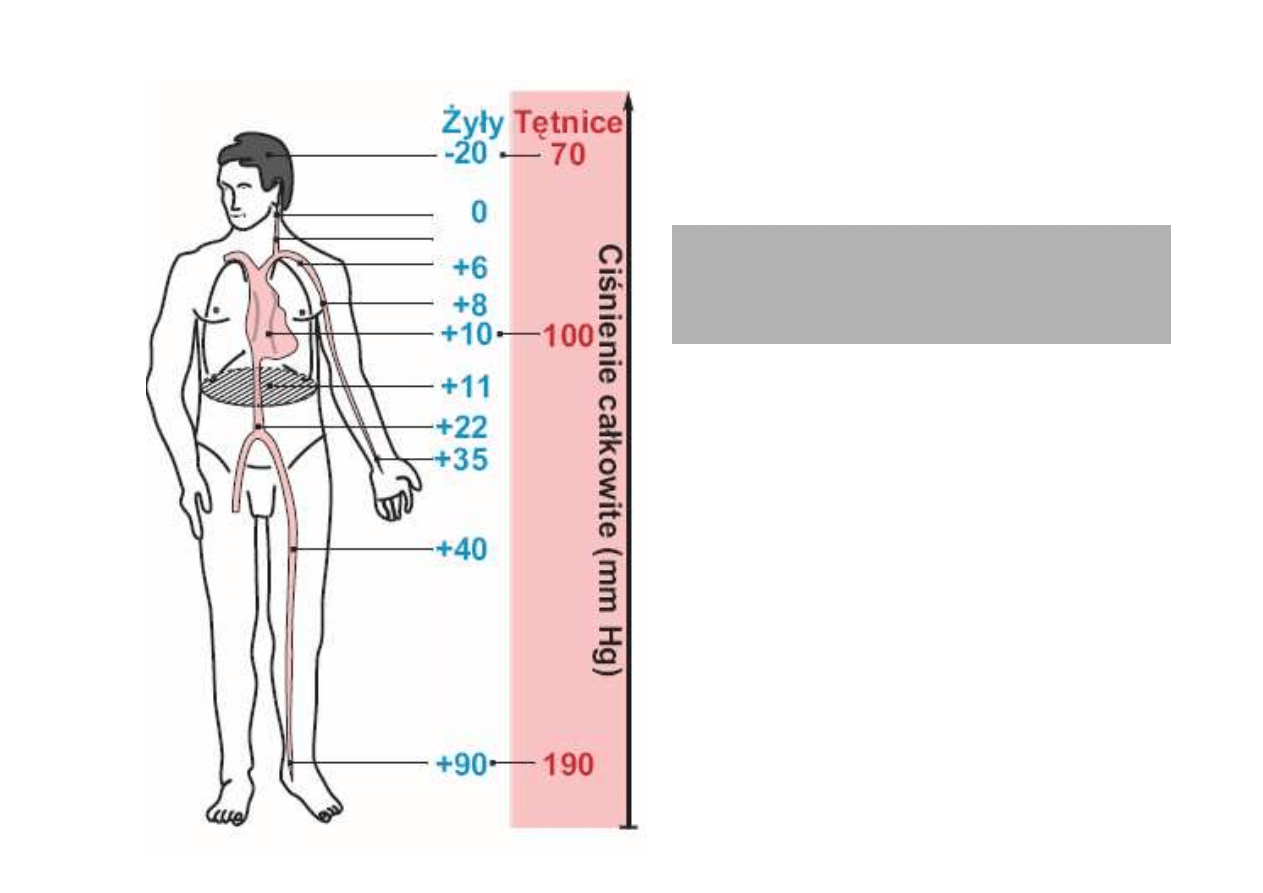
Efekt hydrostatyczny

Ujemne ci

ś

nienie w

ż

yłach czaszki

mo

ż

e powodowa

ć

zasysanie

powietrza przy zranieniu głowy

Efekt hydrostatyczny powoduje
wzrost ci

ś

nienia transmuralnego

(wi

ę

ksza g

ę

sto

ść

krwi od płynu

mi

ę

dzykomórkowego) i ucieczk

ę

wody z naczy

ń

do tkanek

Rozci

ą

gaj

ą

si

ę

te

ż

podatne

ż

yły,

co powoduje akumulacj

ę

krwi –

do 500 ml przy zamianie pozycji
na stoj

ą

c

ą

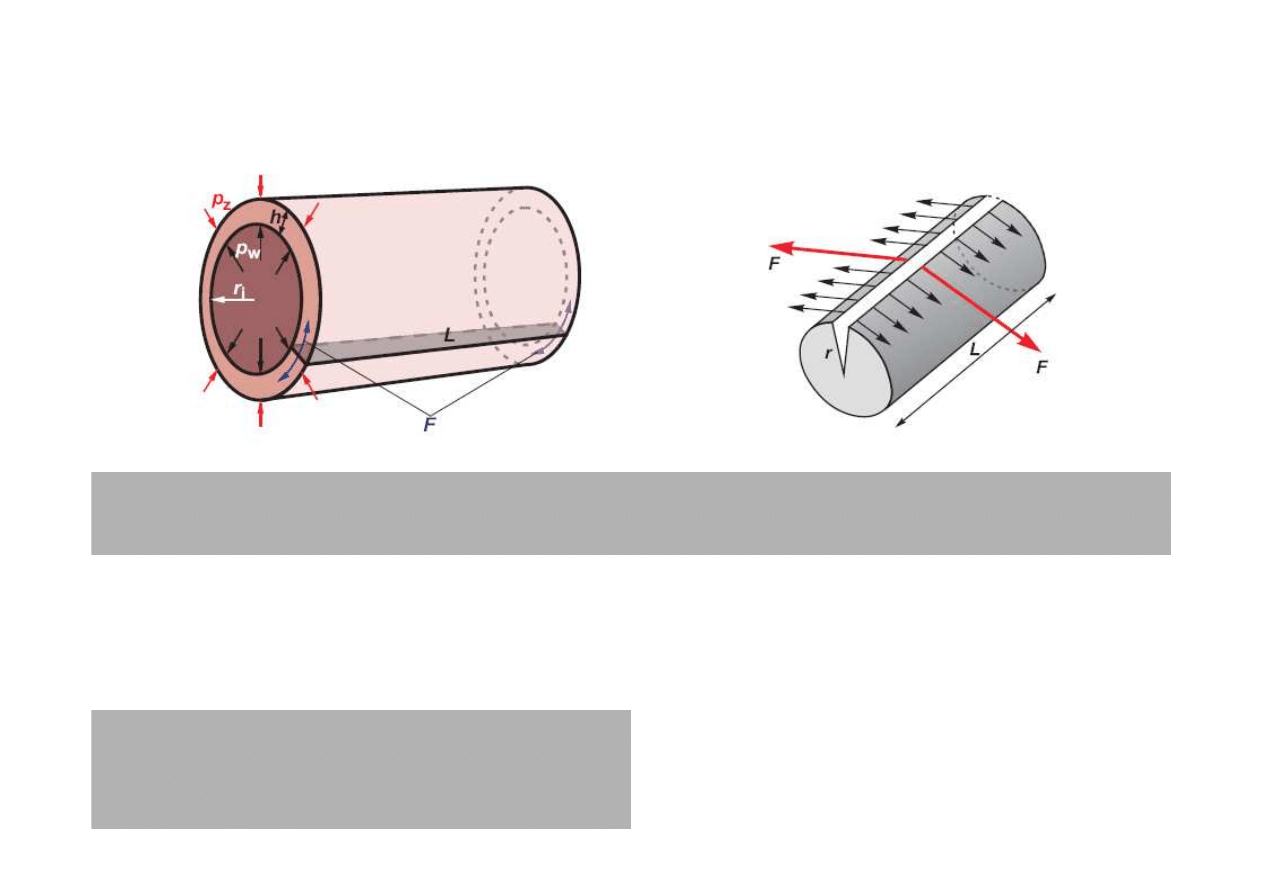
Napr

ęż

enia spr

ęż

yste

ś

cian naczynia

Napr

ęż

enie (napi

ę

cie) spr

ęż

yste poprzeczne = F/L = p *r* L /L = p*r

Napr

ęż

enie podłu

ż

ne = F/2

π

r = p*

π

*r

2

/ 2

π

r = p*r/2

Ci

ś

nienie transmuralne to ró

ż

nica pomi

ę

dzy ci

ś

nieniem krwi i ci

ś

nieniem

zewn

ę

trznym (panuj

ą

cym w tkankach otaczaj

ą

cych naczynie) p = p

w

- p

z

Ze wzgl

ę

du na wi

ę

ksze ci

ś

nienie,

napr

ęż

enia spr

ęż

yste s

ą

wi

ę

ksze w

t

ę

tnicach ni

ż

w

ż

yłach

Najwi

ę

ksze dla du

ż

ych naczy

ń

Aorta T = 200 N/m
Naczynia włosowate T = 0,016 N/m

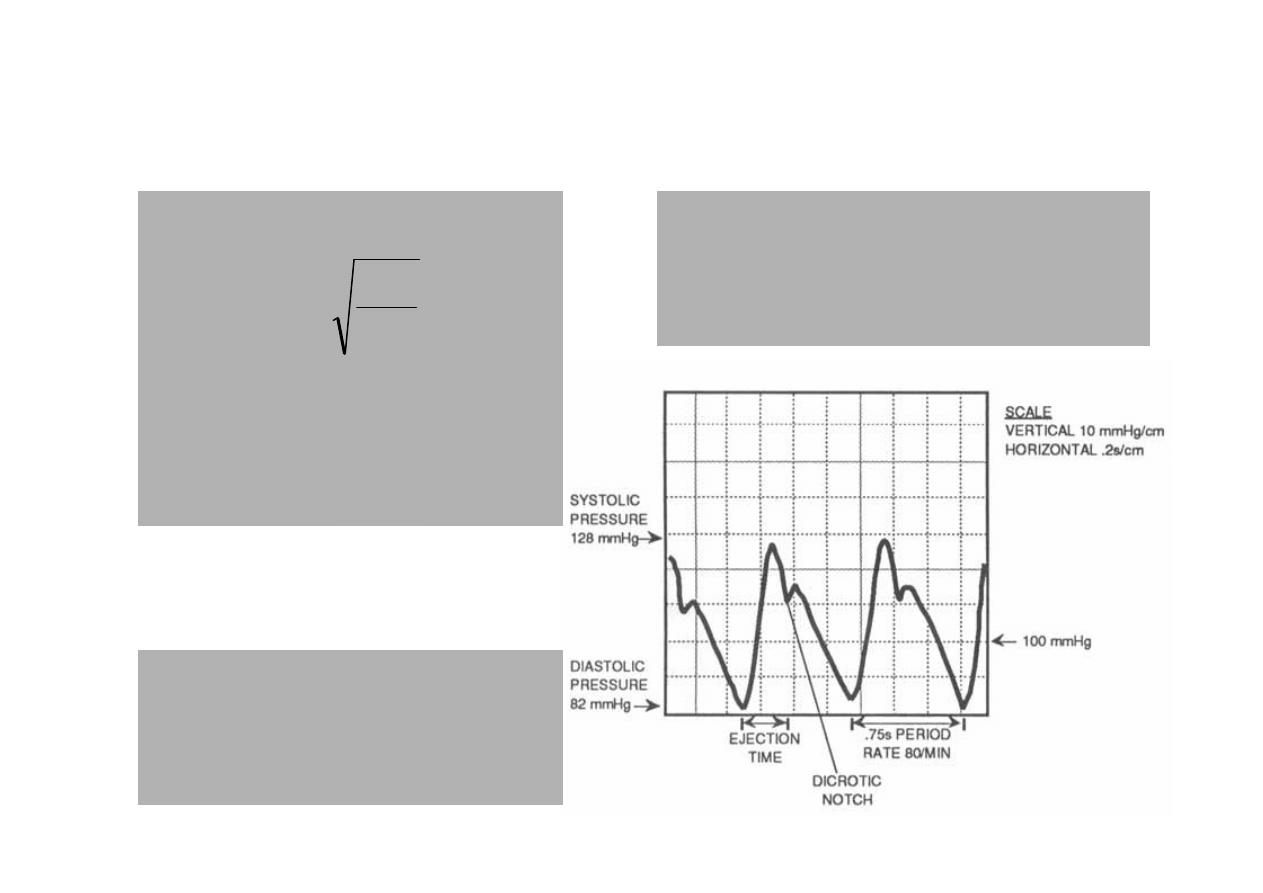
Fala t

ę

tna

Pr

ę

dko

ść

fali t

ę

tna

E – moduł Younga
h – grubo

ść

naczynia

ρ

– g

ę

sto

ść

krwi

r

–

promie

ń

naczynia

r

Eh

c

ρ

2

=

Pr

ę

dko

ść

fali t

ę

tna 5 – 8 [m/s]

Długo

ść

fali t

ę

tna to kilka metrów:

5 [m/s] * 0.8 [1/s] = 4 [m]

Nie mylmy pr

ę

dko

ś

ci fali t

ę

tna

z pr

ę

dko

ś

ci

ą

krwi –

w t

ę

tnicach krew płynie

z pr

ę

dko

ś

ci

ą

rz

ę

du 0,5 [m/s]

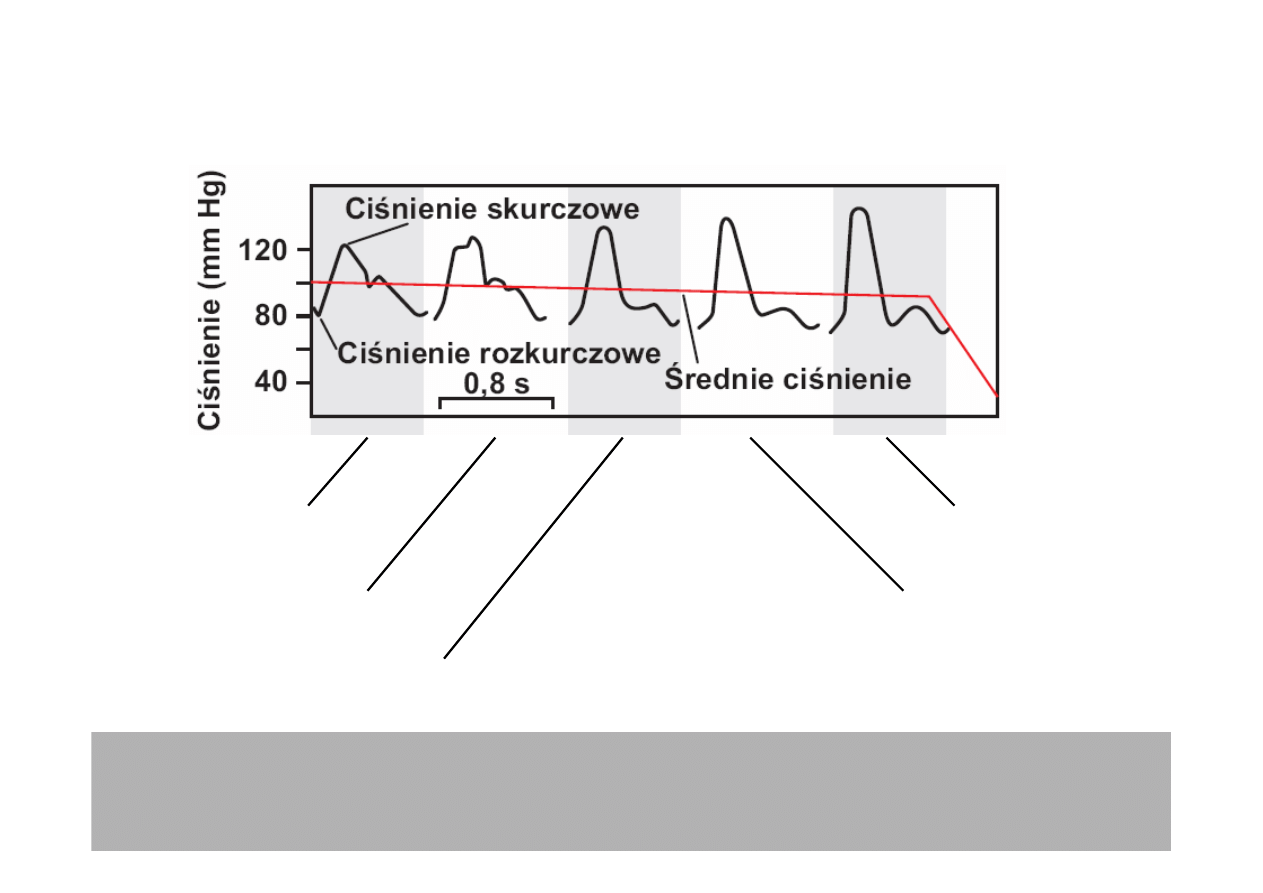
Ewolucja fali t

ę

tna

aorta zst

ę

puj

ą

ca

aorta piersiowa

aorta brzuszna

t

ę

tnica biodrowa

t

ę

tnica podskórna

W najwi

ę

kszych t

ę

tnicach ro

ś

nie (!) ci

ś

nienie skurczowe. Spada ci

ś

nienie

rozkurczowe i ci

ś

nienie

ś

rednie. W mniejszych t

ę

tnicach nast

ę

puje gwałtowny

spadek ci

ś

nienia oraz zanik amplitudy ci

ś

nienia (czyli zanik t

ę

tna)

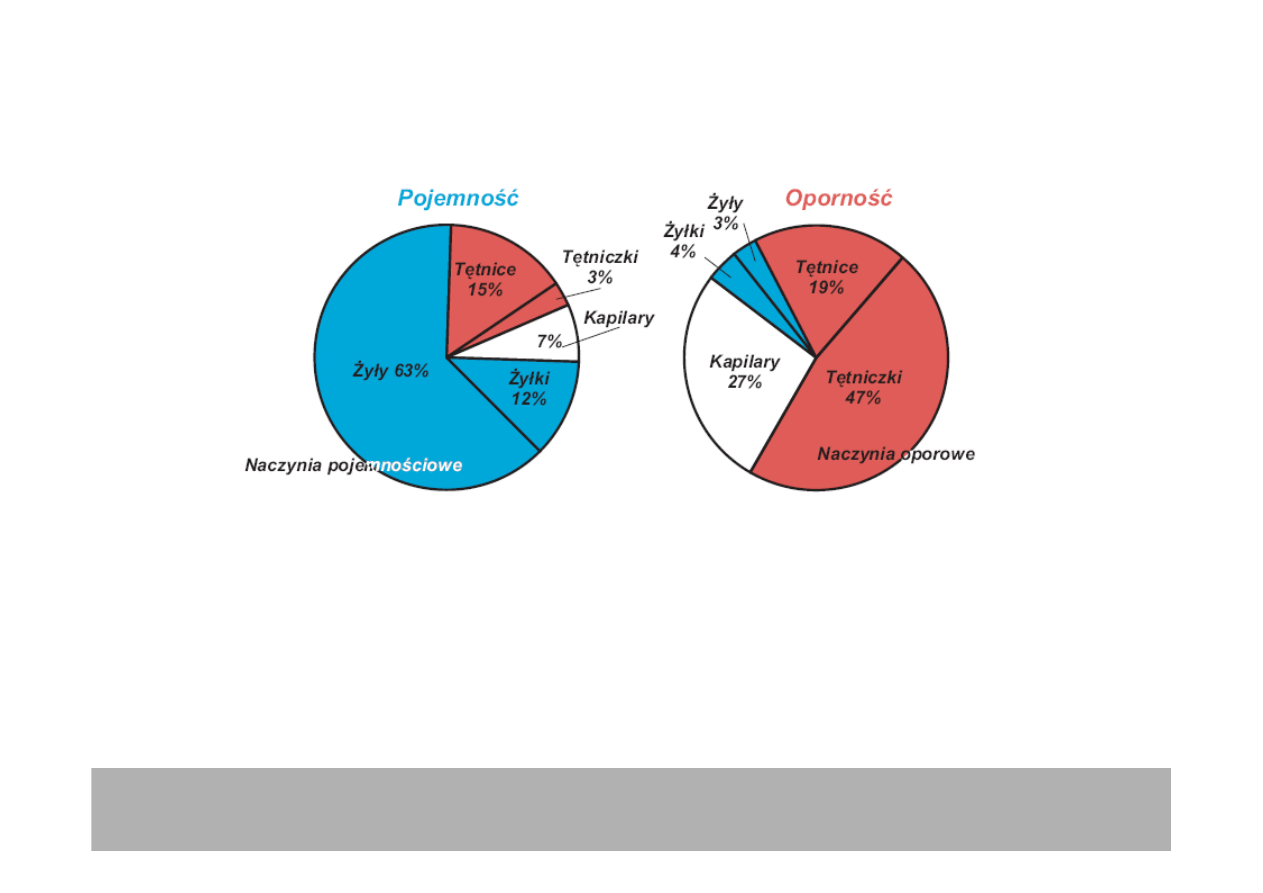
Układ

ż

ylny

ś

yły pełni

ą

funkcj

ę

zbiornika krwi. W przypadku wstrz

ą

su hipowolemicznego,

jako reakcja obronna, mo

ż

e nast

ą

pi

ć

skurcz

ż

ył. Dlatego przy podejrzeniu

wykrwawienia nale

ż

y niezwłocznie zało

ż

y

ć

wenflon – przy skurczonych

ż

yłach

jest to niezwykle trudne.
Oczywi

ś

cie podczas wstrz

ą

su, dystrybucja krwi jest znacz

ą

co inna

Krew w

ż

yłach płynie dzi

ę

ki ró

ż

nicy ci

ś

nie

ń

, pompie mi

ęś

niowej działaj

ą

cej

wraz z systemem zastawek

ż

ylnych