S

TRATY MOCY W ELEMENTACH ENERGOELEKTRONICZNYCH

Przepływ pr du w elemencie półprzewodnikowym powoduje wydzielanie si ciepła.

Moc tracon (rozpraszan lub zamienian na ciepło) odnosimy do poszczególnych stanów pracy

elementu bez próby jej lokalizacji w strukturze. Całkowita moc tracona, b d ce sum strat: zał czania,

wył czania, przewodzenia, blokowania, blokowania w kierunku wstecznym (zaworowe), oraz

zał czania w obwodzie bramki (bazy) wynosi:

P

P

P

P

P

P

P

c

on

off

T

D

R

G

=

+

+

+

+

+

Prze doborze elementu półprzewodnikowego uwzgl dniamy zwykle straty znacz ce, natomiast

pozostałe - dla uproszczenia oblicze - pomijamy. Straty przypisane poszczególnym stanom pracy s

charakterystyczn cech poszczególnych elementów półprzewodnikowych i warunków ich pracy.

Straty mocy w stanie przewodzenia

- warto chwilowa :

( )

( ) ( )

p

t

u

t i

t

T

T

T

ω

ω

ω

=

⋅

,

gdzie napi cie przewodzenia opisane z uwzgl dnieniem parametrów charakterystyki statycznej wynosi

:

( )

( )

u

t

U

r i

t

T

TO

T

T

ω

ω

=

+ ⋅

I

T

r

T

U

T

U

TO

Charakterystyka statyczna w stanie przewodzenia

-warto rednia:

( ) ( )

( ) ( )

( ) ( )

P

p

t d t

U

i

t d t

r

i

t d t

P

U

I

r I

U

I

r k I

T

T

TO

T

T

T

T

TO

AV

T

RMS

TO

AV

T

i

AV

z

w

z

w

z

w

=

=

⋅

+ ⋅

=

⋅

+ ⋅

=

⋅

+ ⋅ ⋅

1

2

1

2

1

2

2

2

2

2

2

π

ω ω

π

ω ω

π

ω ω

α

α

α

α

α

α

W ostatnim równaniu u yto współczynnik kształtu pr du b d cy ilorazem warto ci skutecznej i

warto ci redniej, okre lony za pomoc wzoru:

k

I

I

i

RMS

AV

=

s_3203 J. Piłaci ski: Podstawy energoelektroniki - materiały do wykładu.

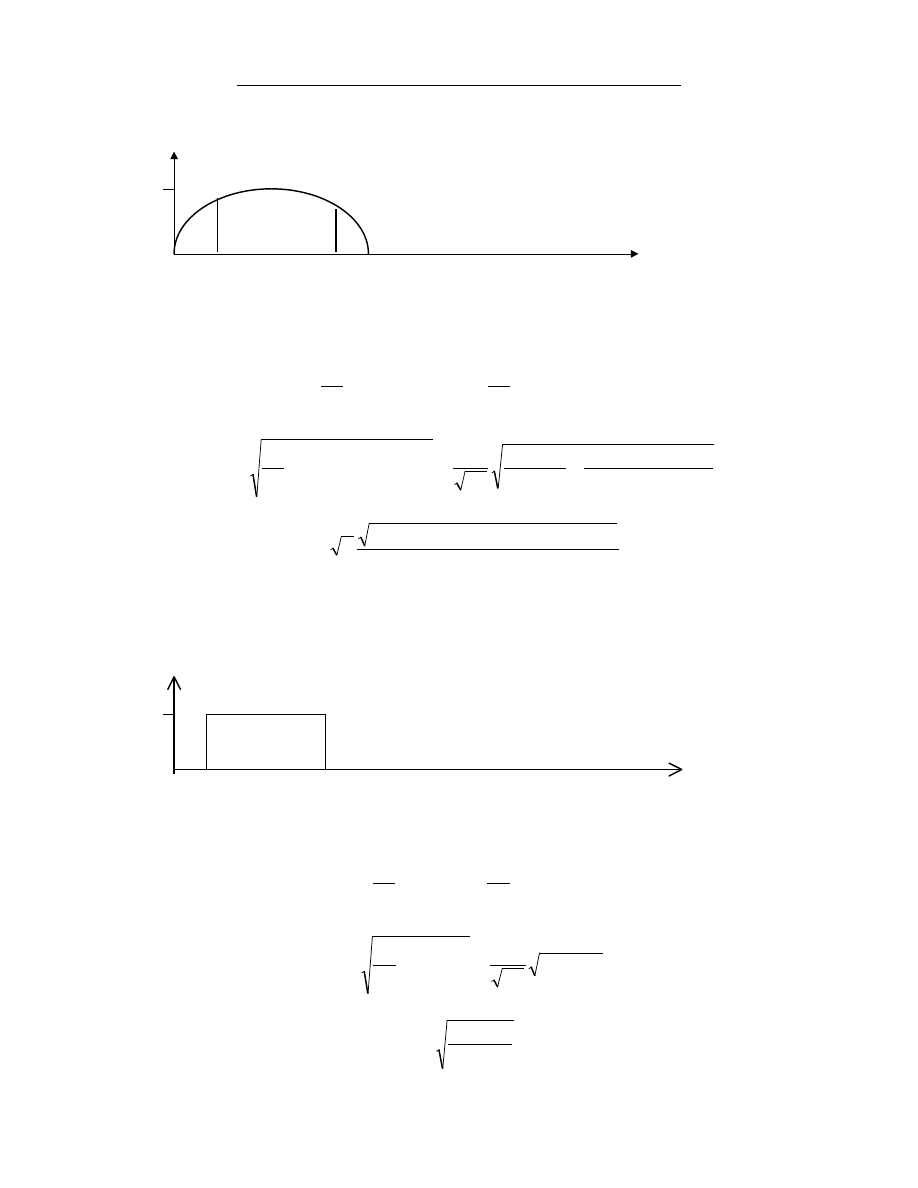
W

SPÓŁCZYNNIK KSZTAŁTU DLA WYBRANYCH PRZEBIEGÓW PR DU

A. Sinusoidalny przebieg pr du.

i

T

I

m

ωt

0

α

z

α

w

π

2

π

( )

( )

i

t

I

t

T

m

ω

ω

=

sin

α ω α

z

w

t

( ) ( )

(

)

I

I

t d t

I

AV

m

m

z

w

z

w

=

=

−

1

2

2

π

ω

ω

π

α

α

α

α

sin

cos

cos

,

( )

(

)

( )

I

I

t d t

I

RMS

m

m

w

z

z

w

z

w

=

=

−

−

−

1

2

2

2

2

2

4

2

π

ω

ω

π

α

α

α

α

α

α

sin

sin

sin

,

k

i

w

z

z

w

z

w

=

−

−

⋅

−

−

π

α

α

α

α

α

α

05

2

2

. (sin

sin

)

cos

cos

.

B. Prostok tny przebieg pr du.

i

T

I

m

ωt

∝

z

∝

w

π

2

π

i

t

I

T

m

( )

ω =

α ω α

z

w

t

( )

(

)

I

I d t

I

AV

m

m

w

z

z

w

=

=

−

1

2

2

π

ω

π

α

α

α

α

,

( )

I

I d t

I

RMS

m

m

w

z

z

w

=

=

−

1

2

2

2

π

ω

π

α

α

α

α

,

k

i

w

z

=

−

2

π

α

α

.

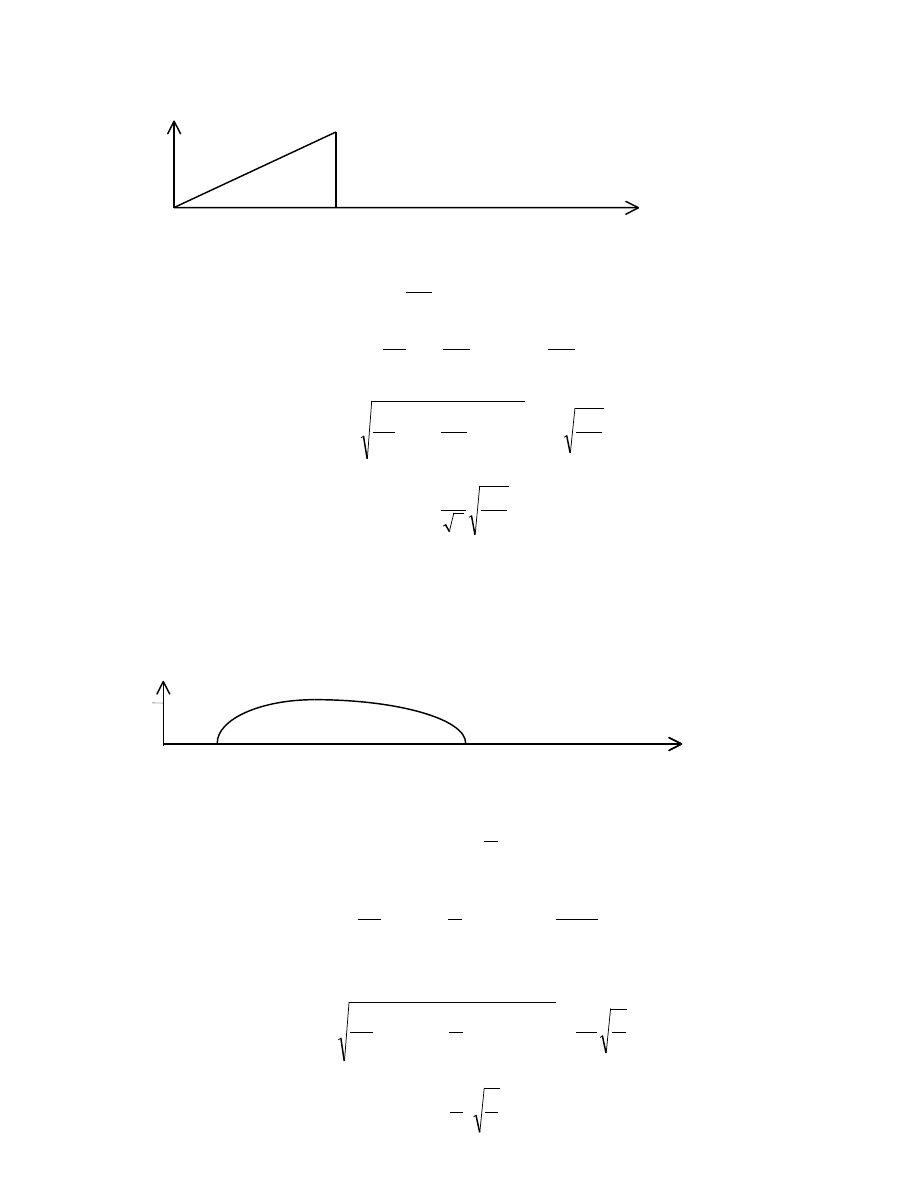
C. Trójk tny przebieg pr du.

i

T

ωt

0

α

w

π

2

π

i

t

I

t

T

m

w

( )

ω

ω

α

=

,

0

ω α

t

w

,

( )

I

I

t

d t

I

AV

m

w

m

w

w

=

=

1

2

4

0

π

ω

α

ω

α

π

α

,

( )

I

I

t

d t

I

RMS

m

w

m

w

w

=

=

1

2

6

2

0

π

ω

α

ω

α

π

α

,

k

i

w

= 4

6

π

α

.

D. Odkształcony przebieg pr du (odbiornik RL)

α

α

λ

w

z

−

=

I

m

ωt

0

α

z

π

α

w

2

π

( )

i t

I

t

m

ω

π
λ

ω

≈

⋅

sin

,

.

( )

I

I

t d t

I

AV

m

m

z

w

=

⋅

=

⋅

1

2

2

π

π

λ

ω

ω

λ

π

α

α

sin

,

.

( )

I

I

t

d t

I

RMS

m

m

z

w

=

⋅

=

1

2

2

2

π

π

λ

ω

ω

λ

π

α

α

sin

,

k

i

= ⋅

π

π
λ

2

.

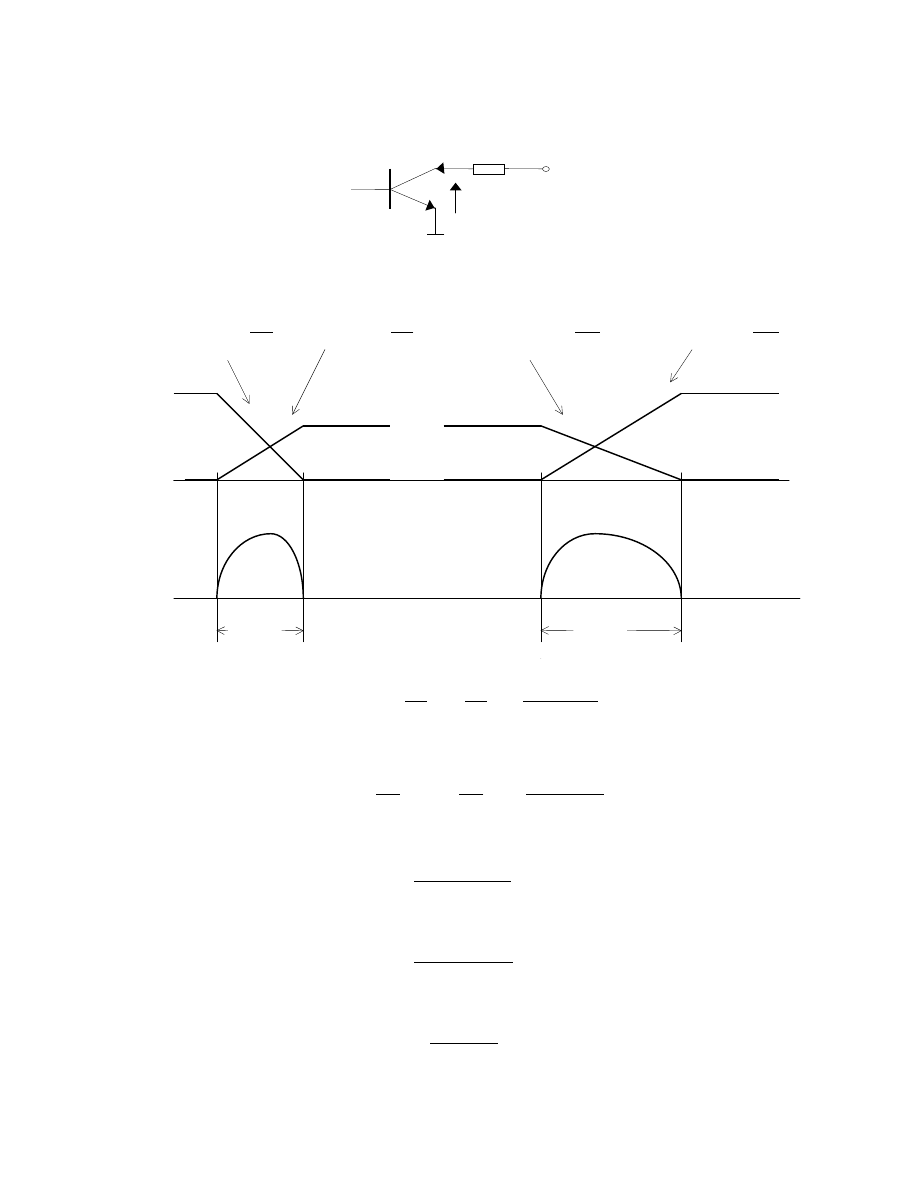
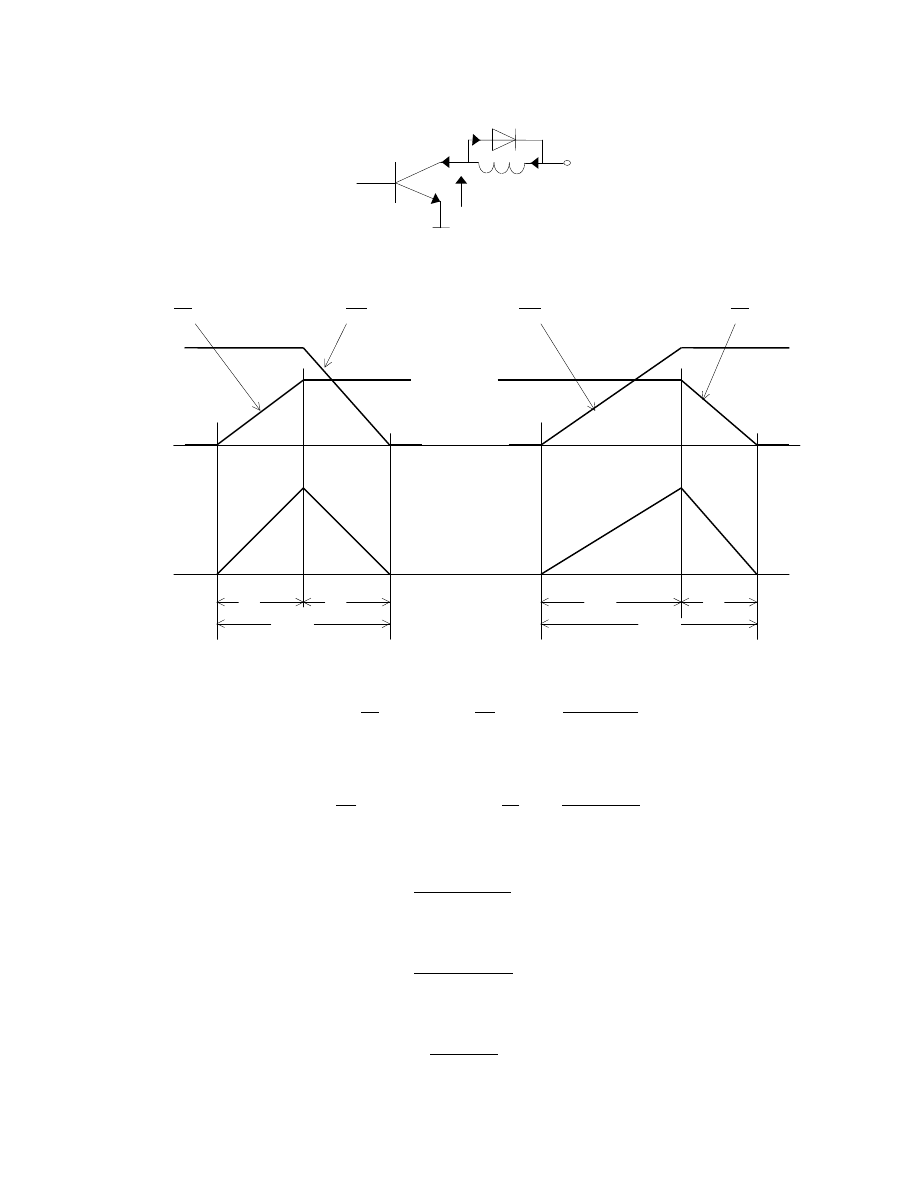
S

TRATY ENERGII I MOC WYDZIELANA PODCZAS ZAŁ CZANIA I WYŁ CZANIA TRANZYSTORA

OBCI

ONEGO REZYSTANCJ

v

V

t

t

ce

s

on

=

−

1

i

I

t

t

ce

m

on

=

i

I

t

t

v

V

t

t

c

m

off

ce

s

off

=

−

=

1

. . . . . . . . . . . . . . . . . .

t

on

t

off

W

V

t

t

I

t

t

dt

V I t

J

on

s

on

m

on

s

m

on

t

on

=

−

⋅

=

⋅ ⋅

1

6

0

[ ]

,

W

V

t

t

I

t

t

dt

V I t

J

off

s

off

m

off

t

s

m

off

off

=

⋅

−

=

⋅ ⋅

1

6

0

[ ]

,

P

V I t

f

W

on

s

m

on

s

=

⋅ ⋅

⋅

6

[ ]

,

P

V I t

f

W

off

s

m

off

s

=

⋅ ⋅

⋅

6

[ ]

,

(

)

P

P

P

V I f

t

t

W

s

on

off

s

m

s

on

off

=

+

=

⋅ ⋅

+

6

[ ]

.

i

C

R

+V

S

U

CE

S

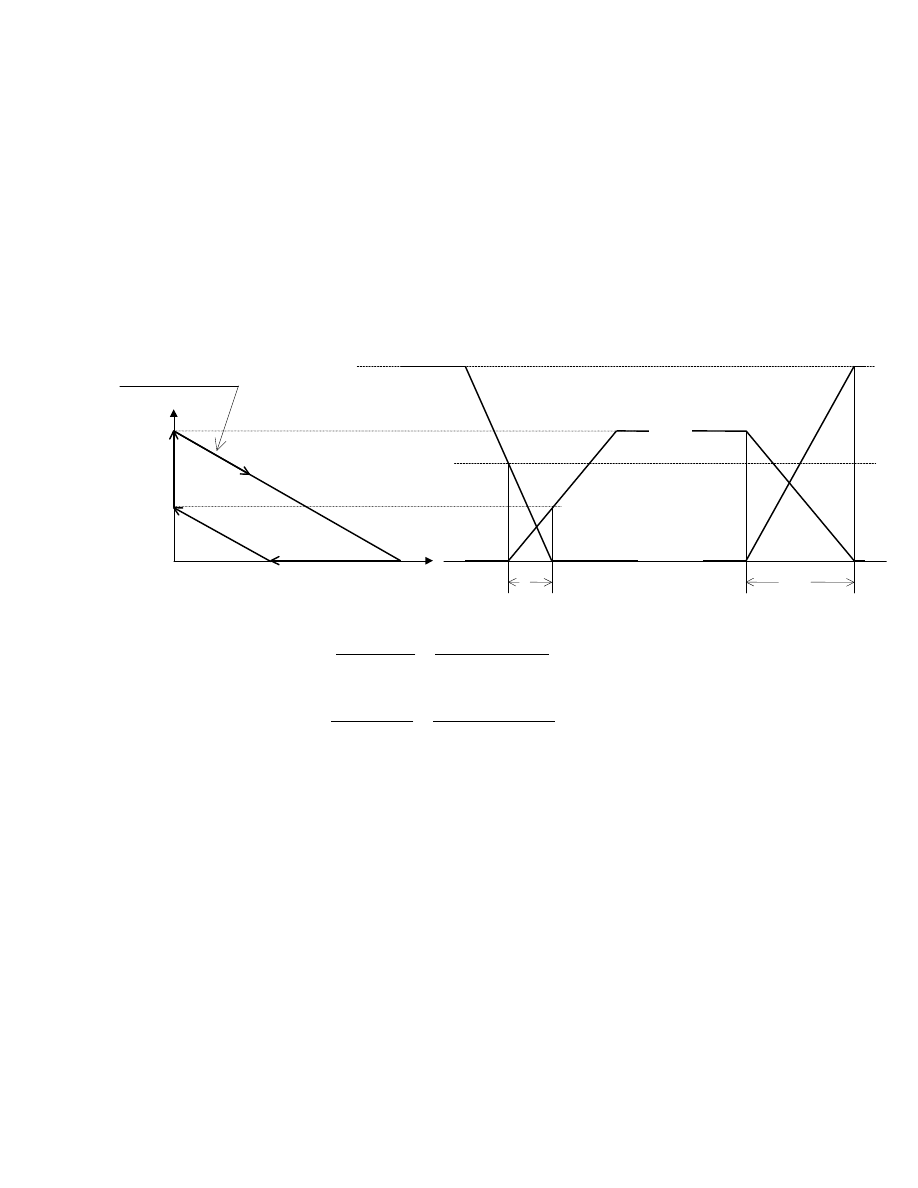
TRATY ENERGII I MOC WYDZIELANA PODCZAS ZAŁ CZANIA I WYŁ CZANIA TRANZYSTORA

OBCI

ONEGO INDUKCYJNO CI

i

I

t

t

v

V

t

t

c

m

ri

ce

s

fv

=

=

−

. . . . . . . . . . . . .

1

v

V

t

t

i

I

t

t

ce

s

rv

c

m

fi

=

=

−

. . . . . . . . . . . . . . . . . . . . . . .

1

t

ri

t

fv

t

rv

t

fi

t

on

t

off

W

V I

t

t

dt

V

t

t

I dt

V I t

J

on

s

m

ri

t

s

fv

m

t

s

m

on

ri

fv

=

⋅

+

−

⋅

=

⋅ ⋅

0

0

1

2

[ ]

,

W

V

t

t

I dt

V I

t

t

dt

V I t

J

off

s

rv

m

t

s

m

fi

t

s

m

off

rv

fi

=

⋅

+

⋅

−

=

⋅ ⋅

0

0

1

2

[ ]

,

P

V I t

f

W

on

s

m

on

s

=

⋅ ⋅

⋅

2

[ ]

,

P

V I t

f

W

off

s

m

off

s

=

⋅ ⋅

⋅

2

[ ]

,

(

)

P

P

P

V I f

t

t

W

s

on

off

s

m

s

on

off

=

+

=

⋅ ⋅

+

2

[ ]

.

i

D

i

C

+V

S

L i

L

U

CE

Przykład:

Dana jest trajektoria punktu pracy tranzystora. Obliczy straty energii podczas zał czania i

wył czania oraz ł czn moc wydzielan podczas przeł czania tranzystora przy cz stotliwo ci

pracy f

s

=10kHz.

Rozwi zanie:

Korzystamy z trajektorii p.pracy tranzystora dla narysowania przebiegów pr du i napi cia. Na

ich podstawie okre lamy rodzaj obci enia.

200V

TRAJEKTORIA

I

c

100A

t

off

=5

µ

s

100V

50A

t

on

=2

µ

s

U

ce

100V 200V t

on

t

off

W

V I

t

mJ

on

s

m

on

=

⋅ ⋅

=

⋅ ⋅ ⋅

=

−

6

100 50 2 10

6

1 667

6

,

W

V I

t

mJ

off

s

m

off

=

⋅ ⋅

=

⋅

⋅ ⋅

=

−

6

200 100 5 10

6

16 67

6

,

P

W

W

f

W

s

on

of

s

=

+

⋅ =

+

⋅

⋅

=

−

(

)

( ,

, )

,

1 667 16 67 10

10

183 4

3

4