2013-03-06

1

Metody probabilistyczne

Metody opisu struktury zbiorowości

Miary zmienności badanej cechy

(rozproszenia, zróżnicowania, dyspersji)

2

Analiza opisowa struktury zjawisk masowych

Miary zmienności

charakteryzują stopień zróżnicowania jednostek

zbiorowości pod względem badanej cechy.

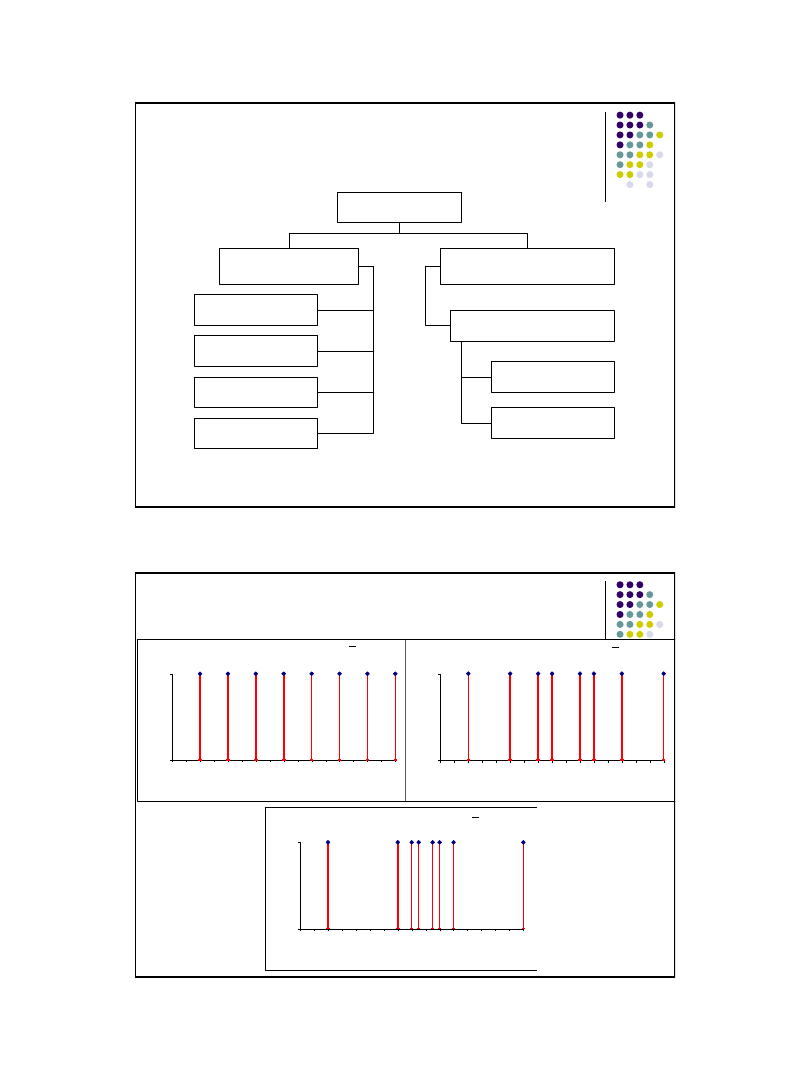
Miary zmienności

Miary pozycyjne

Miary klasyczne

wariancja

pozycyjny

współczynnik

zmienności

odchylenie

ćwiartkowe

rozstęp

współczynik

zmienności

odchylenie

przeciętne

odchylenie

standardowe

2013-03-06

2

3

Miary zmienności

Miary zmienności

Miary względne

(relatywne, stosunkowe)

Miary bezwzględne

(absolutne)

rozstęp

współczynniki zmienności

odchylenie

standardowe

wariancja

odchylenie

ćwiartkowe

klasyczny

pozycyjny

4

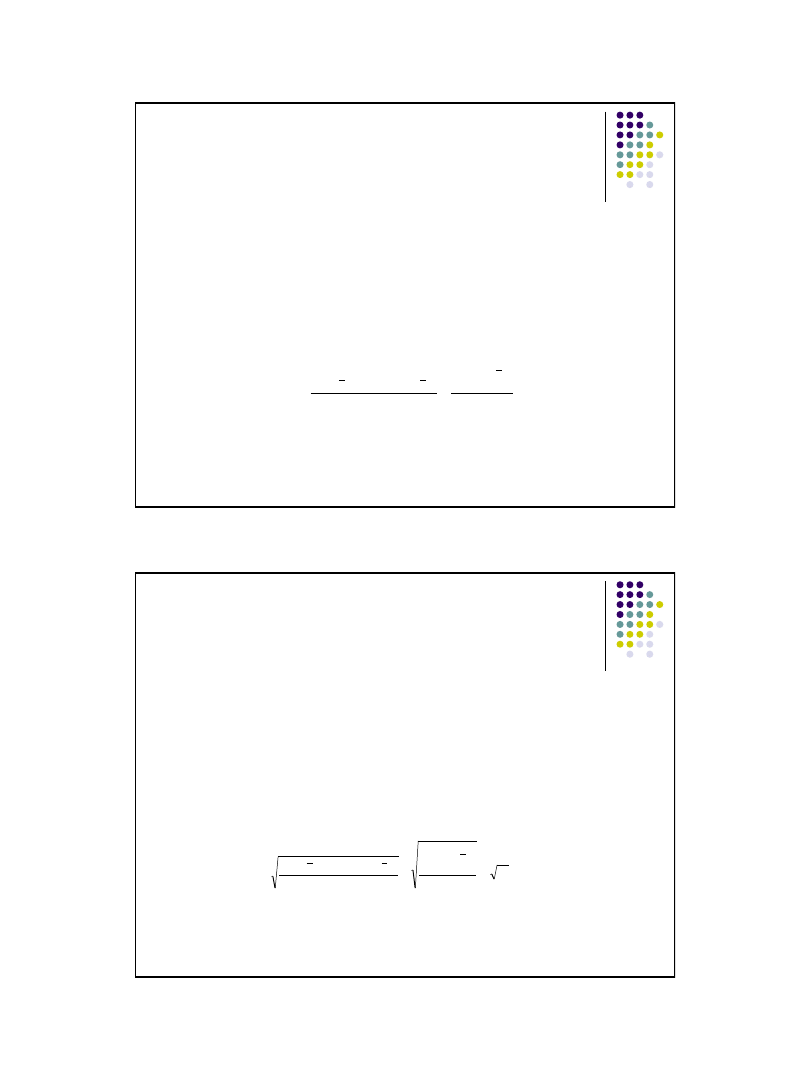
Zmienność w trzech zbiorowościach n=8

0

1

0

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16

f

i

x

i

Zbiorowość A

0

1

0

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16

f

i

x

i

Zbiorowość B

0

1

0

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16

f

i

x

i

Zbiorowość C

9



x

9



x

9



x

2013-03-06

3

5

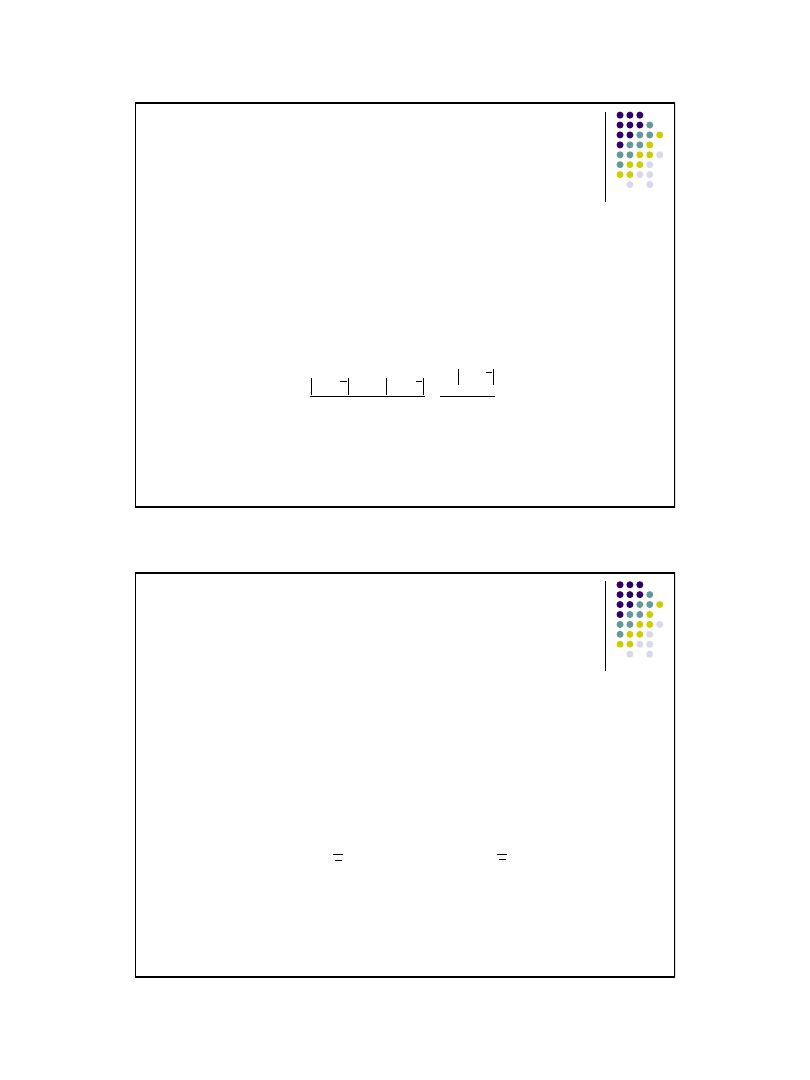
Klasyczne miary zmienności

Wariancję (s

2

)



średnia arytmetyczna kwadratów odchyleń wartości cechy od

średniej arytmetycznej zbiorowości,



wielkość mianowana w kwadracie miana badanej cechy,



nie interpretujemy jej.













n

x

x

n

x

x

x

x

s

n

i

i

n



















1

2

2

2

1

2



6

Klasyczne miary zmienności

Odchylenie standardowe (s)

– niepewność standardowa, dyspersja z próbki



pierwiastek kwadratowy z wariancji.



wielkość mianowaną tak samo jak badana cecha.



określa przeciętne zróżnicowanie badanej cechy od średniej
arytmetycznej.













2

1

2

2

2

1

s

n

x

x

n

x

x

x

x

s

n

i

i

n























2013-03-06

4

7

Klasyczne miary zmienności

Odchylenie przeciętne (d)



średnia arytmetyczna bezwzględnych odchyleń wartości cechy od jej

średniej arytmetycznej,



wielkość mianowana tak samo jak badana cecha,



interpretowany podobnie jak odchylenie standardowe.

n

x

x

n

x

x

x

x

d

n

i

i

n



















1

1



8

Klasyczne miary zmienności

Współczynnik zmienności (klasyczny) (V

s

lub V

d

)



iloraz odchylenia standardowego (lub przeciętnego) przez średnia

arytmetyczną,



wielkość niemianowana,



używany go do porównań zmienności w dwu lub więcej

zbiorowościach.

x

s

V

s



x

d

V

d



lub

2013-03-06

5

9

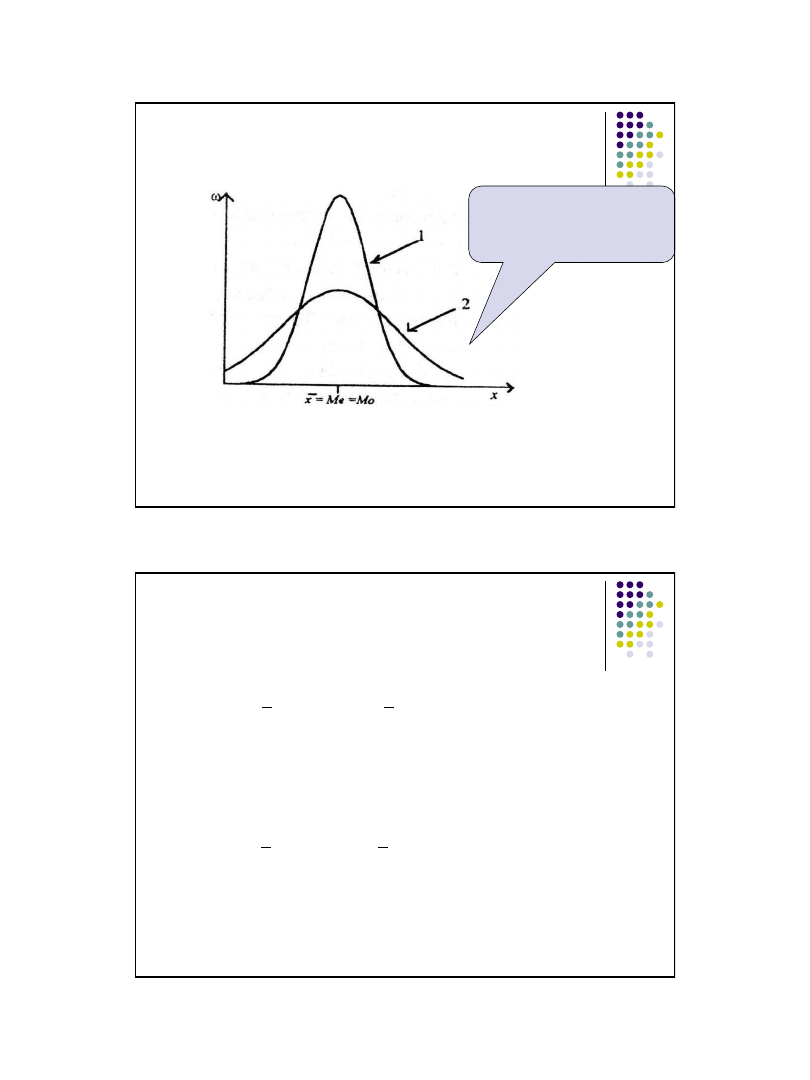
Ocena rozproszenia
na podstawie obserwacji diagramów

1. Mniejsze rozproszenie

wokół średniej

- Diagram jest smuklejszy

i wyższy.

2. Większe rozproszenie wokół średniej

- Diagram jest bardziej

rozłożysty i niższy

Odchylenie standardowe w

zbiorowości (1) jest mniejsze

niż w zbiorowości (2)

s

1



s

2

10

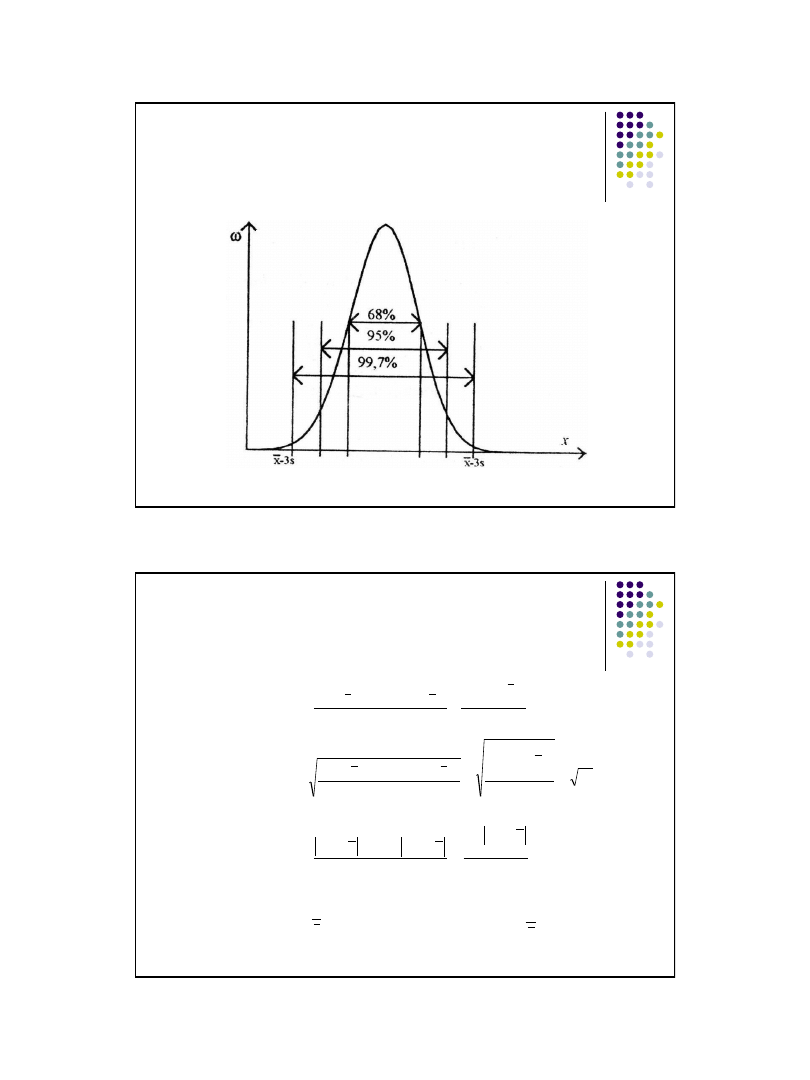
Przedziały wartości cechy – (miary klasyczne)



Przedziały typowe – obszar typowej zmienności

Przedział taki ma tą własność, że około 70% jednostek badanej
zbiorowości charakteryzuje się wartością cechy należącą do tego
przedziału.



Reguła „3 sigm

” - obszar zmienności najbardziej prawdopodobnej

Wystąpienie obserwacji x

i

poza przedziałem określonym

regułą „3 sigm” jest mało prawdopodobne

s

x

x

s

x

typ









s

x

x

s

x

i

3

3









2013-03-06

6

11

Przedziały wartości cechy – (miary klasyczne)

12

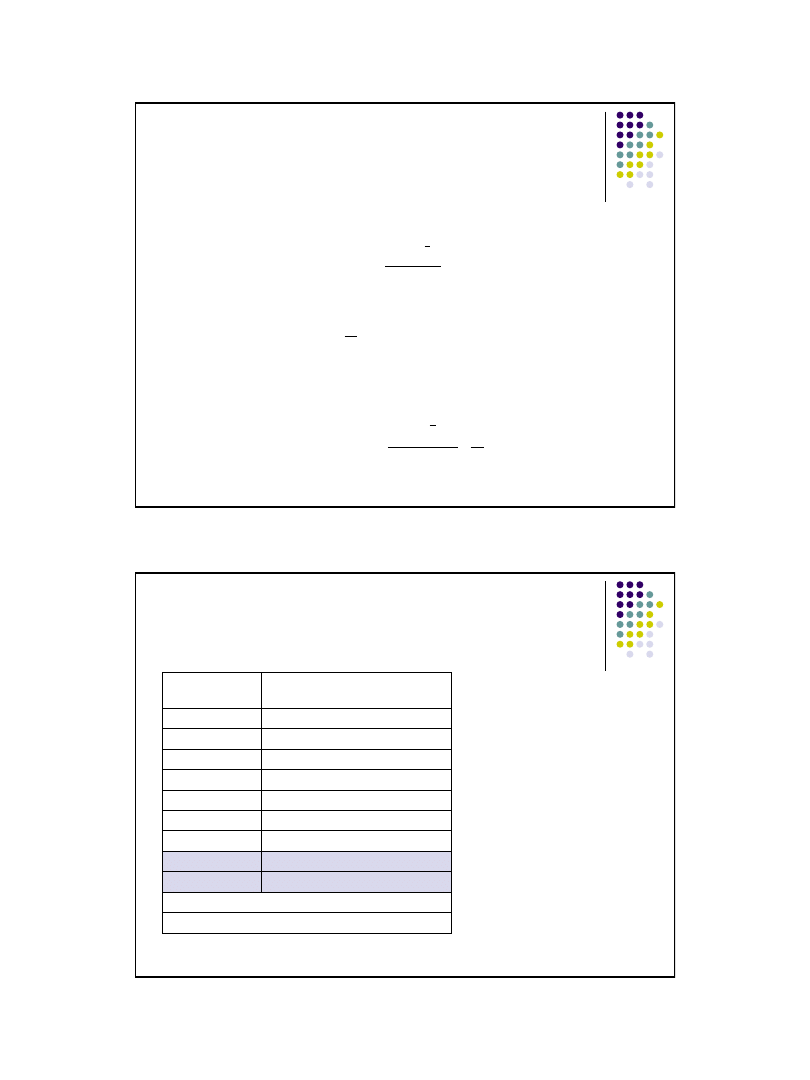
Wyznaczanie wartości miar zmienności
dla szeregów szczegółowych



Wariancja



Odchylenie standardowe



Odchylenie przeciętne



Współczynnik zmienności













n

x

x

n

x

x

x

x

s

n

i

i

n



















1

2

2

2

1

2















2

1

2

2

2

1

s

n

x

x

n

x

x

x

x

s

n

i

i

n























n

x

x

n

x

x

x

x

d

n

i

i

n



















1

1



x

s

V

s



x

d

V

d



lub

2013-03-06

7

13

Poprawki i interpretacje



Poprawka Bessela

– jeżeli wariancja jest liczona

dla małej próby (n≤30)

i

ma być wykorzystana do wnioskowania statystycznego o populacji

generalnej, z której ta próba pochodzi.

Wariancja:



Poprawka Shepparda

niektórzy statystycy twierdzą, że obliczana z szeregów rozdzielczych

przedziałowych (o równych rozpiętościach klas

i liczbie przedziałów <12) wariancja jest przeszacowana i zalecają:





1

1

2

2











n

x

x

s

n

i

i













12

i

2





12

2

1

2

2

i

n

f

x

x

s

k

i

i

i













14

Numer

obserwacji

Liczba osób w kolejce x

i

1

1

=(1-4)

2

=9

=|1-4|=3

2

3

1

1

3

3

1

1

4

3

1

1

5

5

1

1

6

5

1

1

7

8

16

4

suma

28

30

12

średnia

4

= 30/7= 4,29

=12/7=1,71

odchylenie standardowe

2,07

współczynnik zmienności V

s

/V

d

= 2,07/4 = 0,52

=1,71/4=0,43

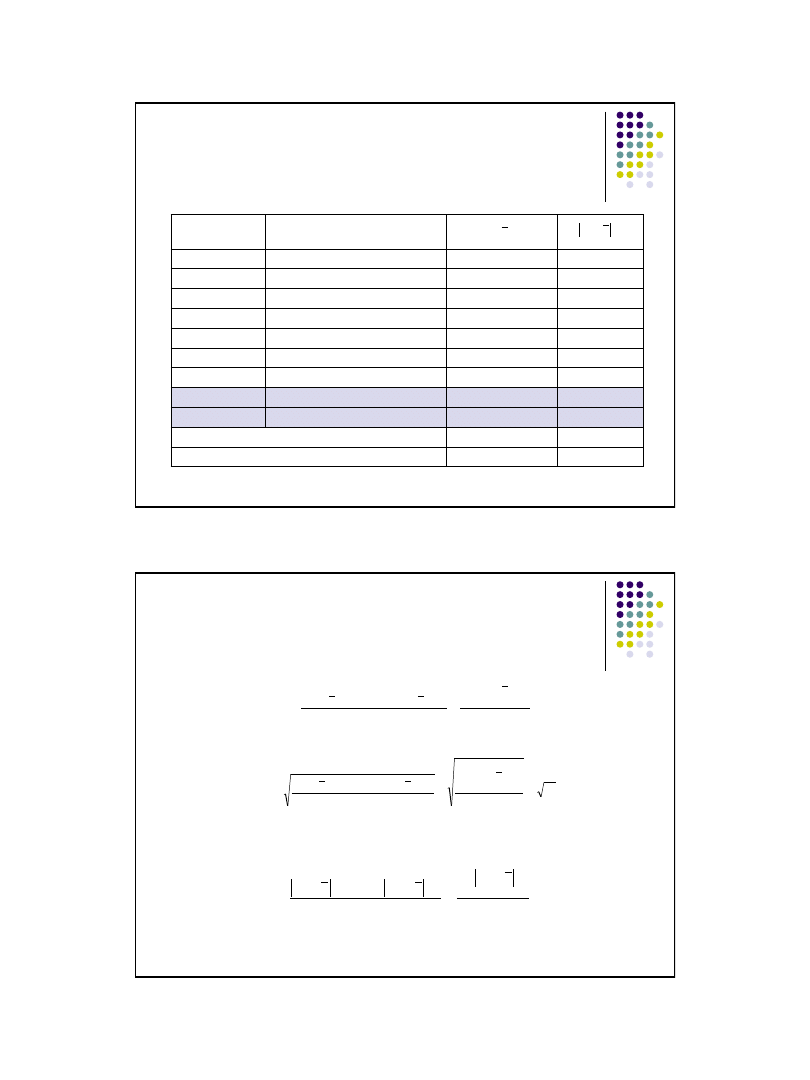
Klasyczne miary zmienności – przykład

szereg szczegółowy





2

x

x

i



x

x

i



2013-03-06

8

15

Klasyczne miary zmienności – przykład

szereg szczegółowy

Numer

obserwacji

Liczba przejazdów x

i

1

1

=(1-4)

2

=9

=|1-4|=3

2

3

1

1

3

3

1

1

4

3

1

1

5

5

1

1

6

5

1

1

7

8

16

4

suma

28

30

12

średnia

4

= 30/7= 4,29

=12/7=1,71

odchylenie standardowe

2,07

współczynnik zmienności V

s

/V

d

= 2,07/4 = 0,52

=1,71/4=0,43





2

x

x

i



x

x

i



16

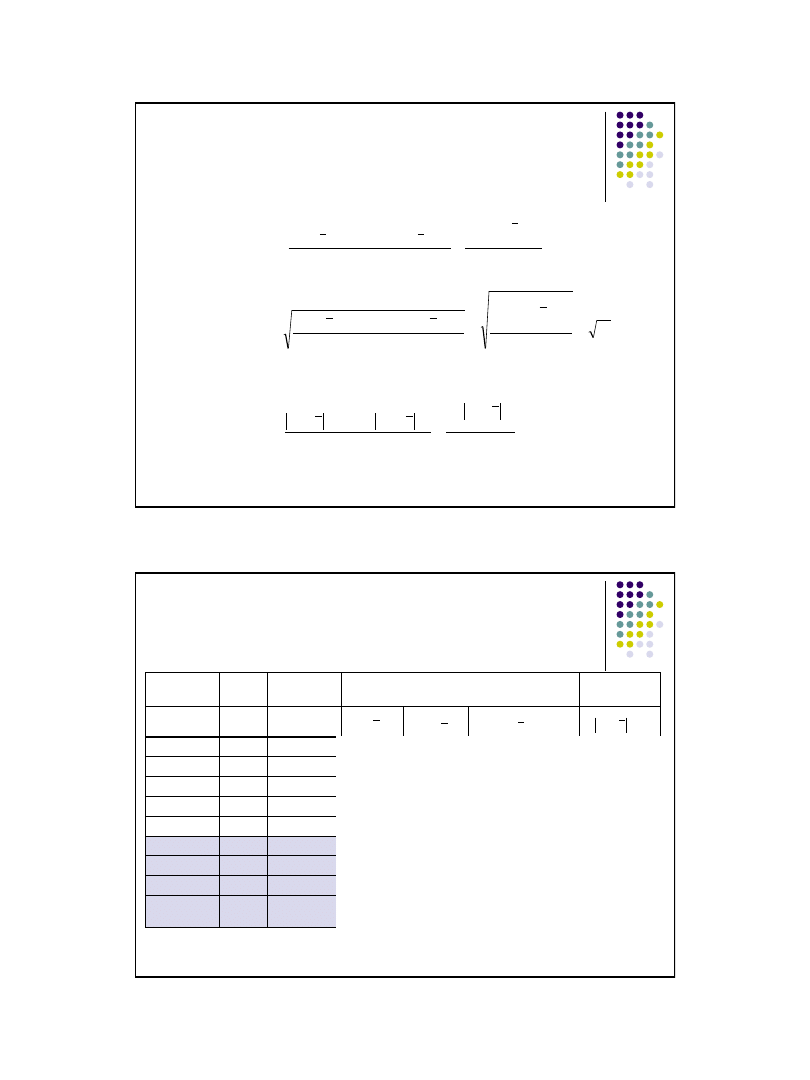
Wyznaczanie wartości miar zmienności
dla szeregów rozdzielczych punktowych



Wariancja



Odchylenie standardowe



Odchylenie przeciętne













n

f

x

x

n

f

x

x

f

x

x

s

k

i

i

i

k

k



















1

2

2

1

2

1

2















2

1

2

2

1

2

1

s

n

f

x

x

n

f

x

x

f

x

x

s

k

i

i

i

k

k























n

f

x

x

n

f

x

x

f

x

x

d

k

i

i

i

k

k



















1

1

1



2013-03-06

9

17

Wyznaczanie wartości miar zmienności
dla szeregów rozdzielczych przedziałowych



Wariancja



Odchylenie standardowe



Odchylenie przeciętne













n

f

x

x

n

f

x

x

f

x

x

s

k

i

i

i

k

k



















1

2

2

1

2

1

2





















2

1

2

2

1

2

1

s

n

f

x

x

n

f

x

x

f

x

x

s

k

i

i

i

k

k





























n

f

x

x

n

f

x

x

f

x

x

d

k

i

i

i

k

k



















1

1

1









18

numer

klasy

liczba

osób

liczba

przypadków

obliczenia dla wariancji

odchylenie

przeciętne

i

x

i

f

i

1

0

15

=0-1=-1

=(0-1)

2

=1

=(0-1)

2

*15=15

=|0-1|*15=15

2

1

25

0

0

0

0

3

2

6

1

1

6

6

4

3

3

2

4

12

6

5

4

1

3

9

9

3

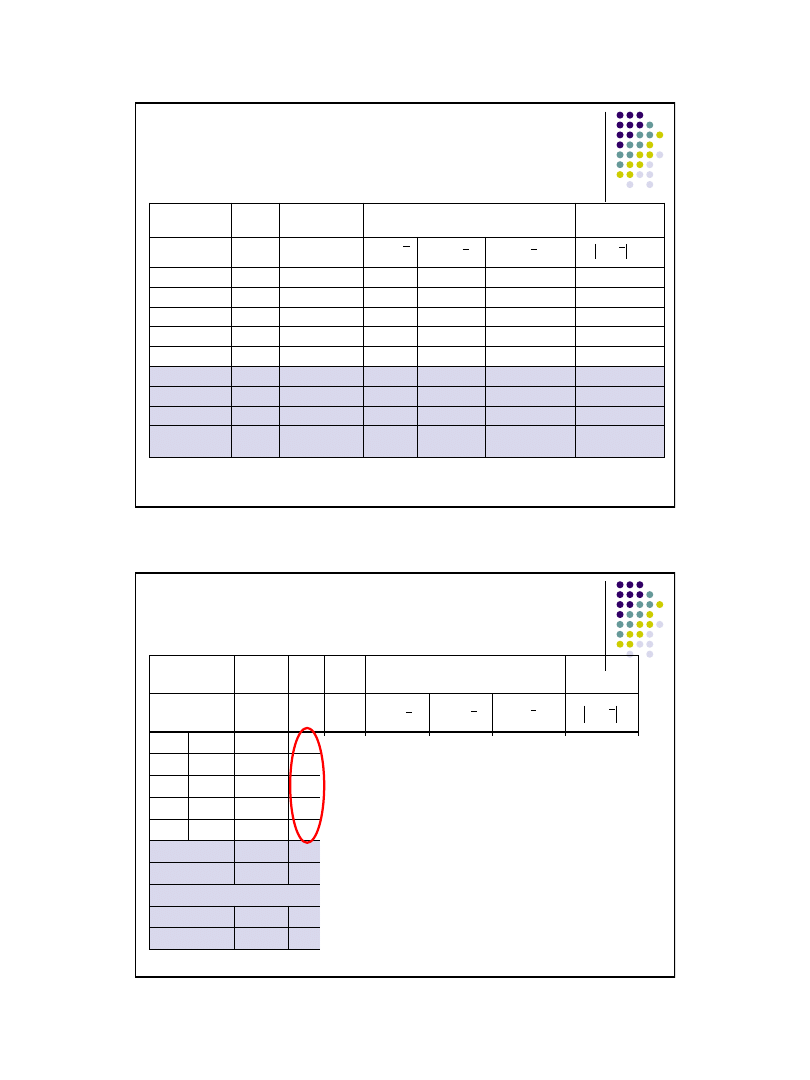
Suma



50





42

30

Średnia

x

śr

=1

=42/50=0,84

=30/50=0,6

Odch.stand

s

0,92

V

s

/ V

d

V

s

/ V

d

=0,92/1=0,92

=0,6/1=0,6

Klasyczne miary zmienności – przykład

szereg rozdzielczy punktowy

x

x

i







2

x

x

i







i

i

f

x

x

2



i

i

f

x

x



2013-03-06

10

19

numer

klasy

liczba

osób

liczba

przypadków

obliczenia dla wariancji

odchylenie

przeciętne

i

x

i

f

i

1

0

15

=0-1=-1

=(0-1)

2

=1

=(0-1)

2

*15=15

=|0-1|*15=15

2

1

25

0

0

0

0

3

2

6

1

1

6

6

4

3

3

2

4

12

6

5

4

1

3

9

9

3

Suma



50





42

30

Średnia

x

śr

=1

=42/50=0,84

=30/50=0,6

Odch.stand

s

0,92

V

s

/ V

d

V

s

/ V

d

=0,92/1=0,92

=0,6/1=0,6

Klasyczne miary zmienności – przykład

szereg rozdzielczy punktowy

x

x

i







2

x

x

i







i

i

f

x

x

2



i

i

f

x

x



obliczenia dla wariancji

odchylenie

przeciętne

Przedział

liczba

firm f

i

0,5

5,5

20

3

60

-11

121

2420

220

5,5

10,5

30

8

240

-6

36

1080

180

10,5

15,5

60

13

780

-1

1

60

60

15,5

20,5

70

18

1260

4

16

1120

280

20,5

25,5

20

23

460

9

81

1620

180

Suma

200

2800

6300

920

Średnia

14

s

2

31,5

4,6

Z poprawką Shepparda

2,08

s

2

–i

2

/12

29,42

Odch.stand

s=

5,61

s

5,42

V

s

/ V

d

V

s

/ V

d

0,39

0,33

20

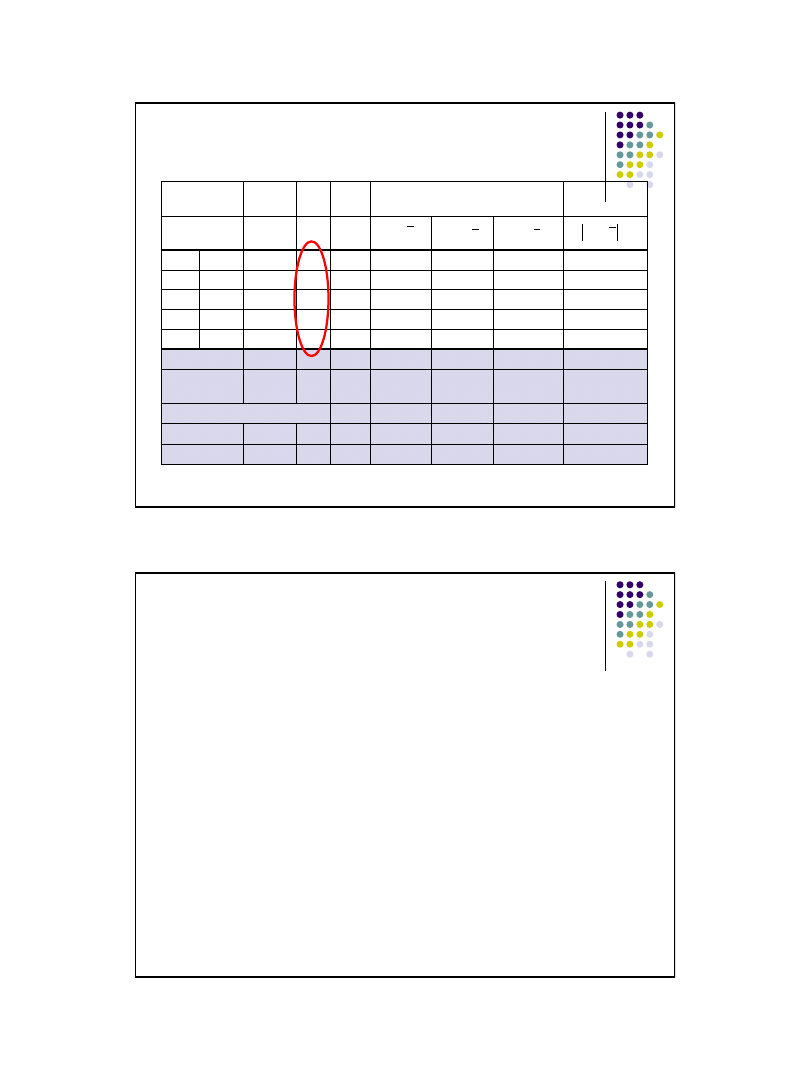
Klasyczne miary zmienności – przykład

szereg rozdzielczy przedziałowy

x

x

i









2

x

x

i









i

i

f

x

x

2





i

i

f

x

x





i

i

f

x

i

x

Poprawka Shepparda =i

2

/12=25/12=2,08333 →s

2

=31,5-

2,08=29,42 →s=5,42

2013-03-06

11

21

obliczenia dla wariancji

odchylenie

przeciętne

Przedział

liczba

firm f

i

0,5

5,5

20

3

60

-11

121

2420

220

5,5

10,5

30

8

240

-6

36

1080

180

10,5

15,5

60

13

780

-1

1

60

60

15,5

20,5

70

18

1260

4

16

1120

280

20,5

25,5

20

23

460

9

81

1620

180

Suma

200

x

2800

x

x

6300

920

Średnia

14

s

2

=6300/200=

31,5

=920/200

=4,6

Z poprawką Shepparda

2,08

s

2

–i

2

/12

29,42

Odch.stand

s=

5,61

s=

5,42

V

s

/ V

d

V

s

/ V

d

0,39

0,33

Klasyczne miary zmienności – przykład

szereg rozdzielczy przedziałowy

x

x

i









2

x

x

i









i

i

f

x

x

2





i

i

f

x

x





i

i

f

x

i

x

Poprawka Shepparda =i

2

/12=25/12=2,08333

→s

2

=31,5-

2,08=29,42 →s=5,42

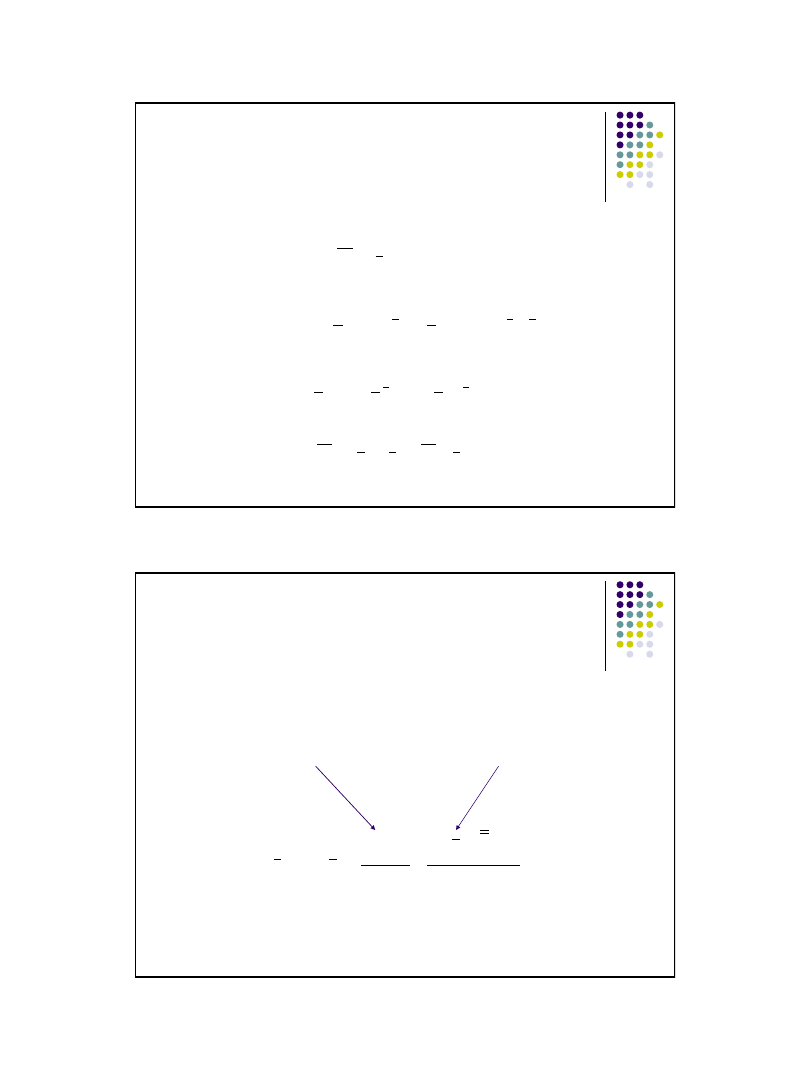
22

Współczynnik zmienności

Interpretacja V:



0 -

10% zróżnicowanie

statystycznie nieistotne,



10

– 20% zróżnicowanie słabe,



20

– 40% zróżnicowanie

umiarkowane,



40

– 60% zróżnicowanie silne,



> 60% zróżnicowanie bardzo silne,



V>20%

badana cecha

charakteryzuje się dużą zmiennością

.

Zeliaś A, Pawelek B, Wanat S.,. Metody statystyczne.
Zadania i sprawdziany str.57

Interpretacja V

(badania marketingowe)



0 - 35% cecha

słabo

zróżnicowana

lub względnie

jednorodna,



35

– 65% cecha zróżnicowana w

stopniu umiarkowanym

,



> 65% cecha zróżnicowanie

bardzo silnie

,

Rószkiewicz M. Narzędzia statystyczne w analizach
marketingowych str.7

2013-03-06

12

23

Własności wariancji



Wariancja jest

różnicą między średnią arytmetyczną kwadratów wartości

zmiennej i kwadratem jej średniej arytmetycznej

, czyli:

 

2

2

2

x

x

s

































k

i

i

i

k

i

i

x

x

x

x

n

x

x

n

s

1

2

2

1

2

2

2

1

1

 

 

 





















k

i

k

i

i

k

i

i

x

n

x

x

n

x

n

1

2

1

1

2

1

2

1

2

2

2

2

2

2

x

x

x

x

x











24

Własności wariancji



Własność równości wariancyjnej:



jeżeli zbiorowość zostanie podzielona na r grup,



to wariancja ogólna (całej zbiorowości) jest sumą dwóch składników:

wariancji wewnątrzgrupowej i wariancji międzygrupowej:

 

 

n

f

x

x

n

f

s

x

s

s

s

r

i

i

i

r

i

i

i



















1

2

1

2

2

2

2

2013-03-06

13

25

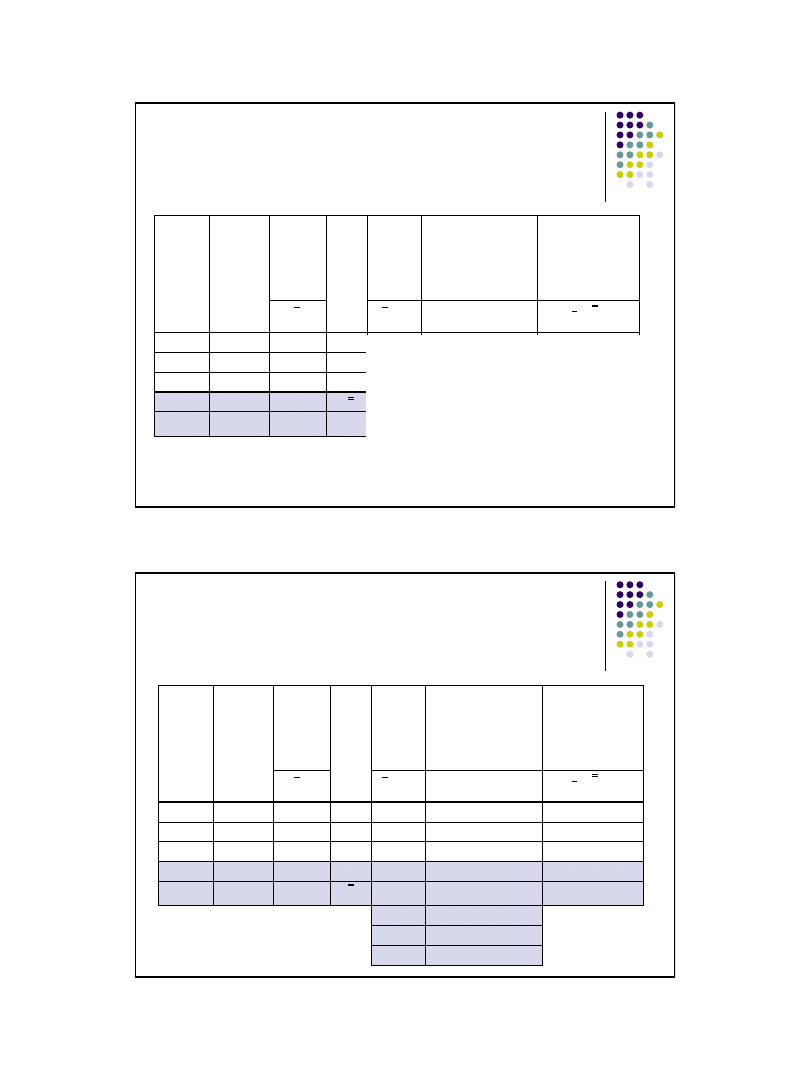
Równości wariancyjna – przykład

zbiorowość podzielona na 3 grupy



2

s

Zakład

Liczba

osób f

i

Średni

staż

pracy

waria

ncja

Średnia

dla sieci

Wariancja

wewnątrzgrupowa

Wariancja

międzygrupowa

A

30

12

3

360

90

218,7

B

100

8

2

800

200

169

C

70

10

4

700

280

34,3

Suma

200





1860

570

422

Średnia

9,3

2,85

2,11

s

2

=

4,96

s=

2,23

V(x)=

0,24

x

i

x

2

i

s

i

i

f

x *

i

i

f

s *

2

 

i

i

f

x

x

*

2



26

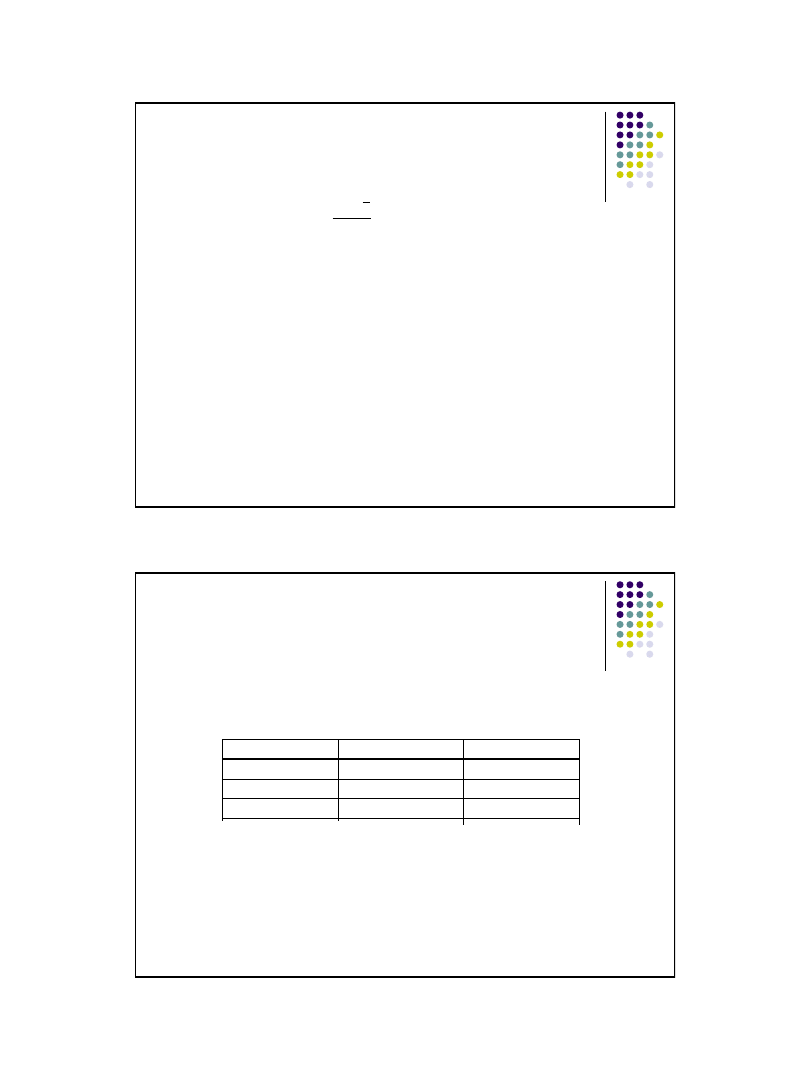
Równości wariancyjna – przykład

zbiorowość podzielona na 3 grupy

i

x

2

i

s

i

i

f

x *

i

i

f

s *

2

 

i

i

f

x

x

*

2





2

s

Zakład

Liczba

osób f

i

Średni

staż

pracy

waria

ncja

Średnia

dla sieci

Wariancja

wewnątrzgrupowa

Wariancja

międzygrupowa

A

30

12

3

360

90

218,7

B

100

8

2

800

200

169

C

70

10

4

700

280

34,3

Suma

200





1860

570

422

Średnia

9,3

2,85

2,11

s

2

=

4,96

s=

2,23

V(x)=

0,24

x

2013-03-06

14

27

Standaryzacja wartości cechy



Wartość standaryzowana informuje o tym, o ile odchyleń standardowych

pierwotna wartość cechy jest większa /mniejsza od średniej arytmetycznej,



Standaryzacji podlegają wyłącznie cechy ilościowe (tylko wtedy można

wyliczyć wartość średnią i odchylenie standardowe),



Średnia arytmetyczna zbioru danych standaryzowanych wynosi 0, a

odchylenie standardowe jest równe 1,



Dane standaryzowane pochodzące z różnych rozkładów mogą być ze

sobą porównywalne.

s

x

x

z

i

i





28

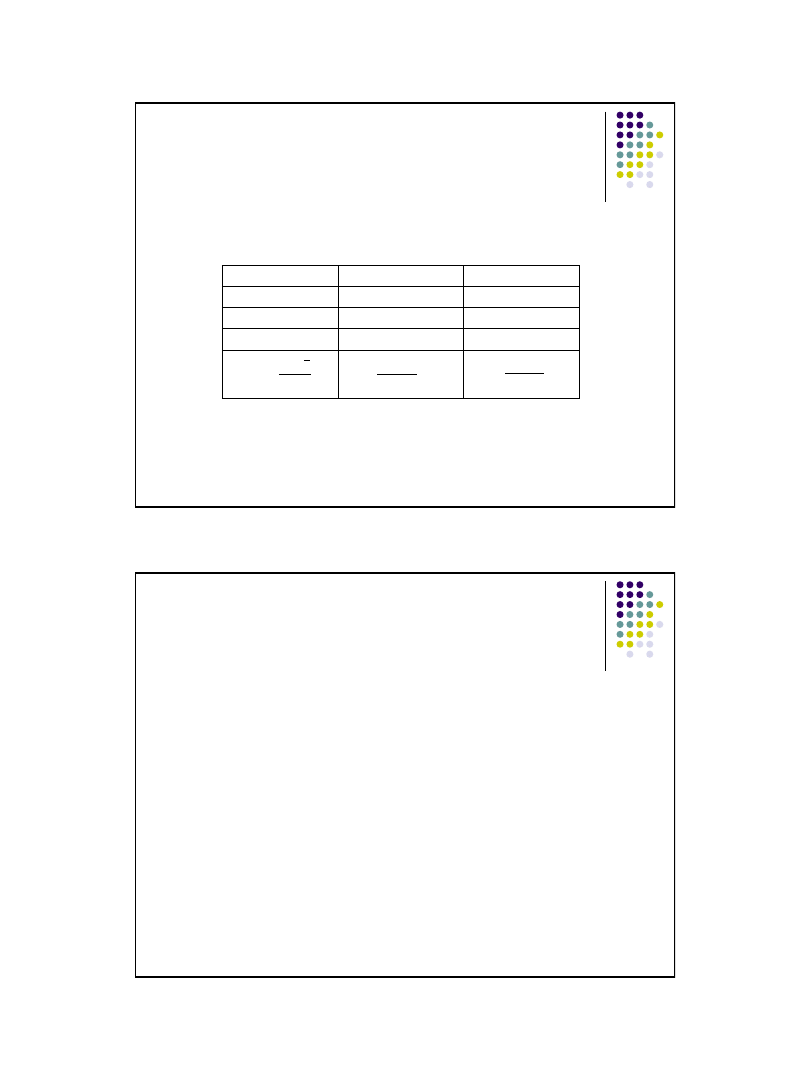
Standaryzacja wartości cechy - przykład

s

x

x

z

i

i





5

0

10

55

60

z

i

,







1

5

45

50

z

i







matematyka

j.angielski

Wynik ucznia

60

50

Średnia klasy

55

45

Odch.stand

10

5

Przykład:

Z jakiego przedmiotu uczeń uzyskał lepsze wyniki na tle klasy

Uczeń był lepszy z j.angielskiego

2013-03-06

15

matematyka

j.angielski

Wynik ucznia

60

50

Średnia klasy

55

45

Odch.stand

10

5

29

Standaryzacja wartości cechy - przykład

s

x

x

z

i

i





5

,

0

10

55

60







i

z

1

5

45

50







i

z

Przykład:

Z jakiego przedmiotu uczeń uzyskał lepsze wyniki na tle klasy

Uczeń był lepszy z j.angielskiego

POZYCYJNE MIARY ZMIENNOŚCI

30

2013-03-06

16

31

Miary pozycyjne



Rozstęp ( R )

definiuje się jako różnicę pomiędzy największą i

najmniejszą wartością cechy:



Odchylenie ćwiatkowe (Q)

definiuje się go jako połowę różnicy

pomiędzy trzecim i pierwszym kwartylem

:



mierzy poziom zróżnicowania połowy jednostek populacji.

jest miarą rozproszenia wartości cechy od mediany,



odrzucane są jednostki o wartościach badanej cechy poniżej pierwszego

kwartyla (25%) oraz powyżej trzeciego kwartyla (25%).

2

1

3

Q

Q

Q





min

max

x

x

R





32

Miary pozycyjne



Współczynnik zmienności V

Q

(pozycyjny)

jest to iloraz

odchylenia ćwiartkowego przez medianę.



wielkość niemianowana.



do porównań zmienności w dwu lub więcej zbiorowościach.



Przedział typowych wartości cechy



Definiujemy go podobnie jak w przypadku miar klasycznych



rolę średniej przejmuje tutaj mediana,



rolę odchylenia standardowego – odchylenie ćwiartkowe,



Przedział ten będzie węższy od przedziału dla miar klasycznych.

e

Q

M

Q

V



1

3

1

3

Q

Q

Q

Q

V

Q







lub

Q

M

x

Q

M

e

typ

e









2013-03-06

17

33

Miary pozycyjne -

przykład



Liczba osób w kolejce do kasy biletowej

x

i

= 1,2,2,3,3,3,3,5,5,6,7,8 n=12



Rozstęp:



Odchylenie ćwiartkowe:



Q

1

= 2,75



Q

2

(Me) = x

6

+ x

7

= (3+3)/2=3



Q

3

= 5,25



Współczynnik
zmienności
(pozycyjny):



Przedział typowych
wartości cechy
(pozycyjny):

7

1

8

min

max











x

x

R

25

,

1

2

75

,

2

25

,

5

2

1

3











Q

Q

Q

42

,

0

3

25

,

1







e

Q

M

Q

V

25

,

4

75

,

1

25

,

1

3

25

,

1

3





















typ

typ

e

typ

e

x

x

Q

M

x

Q

M

34

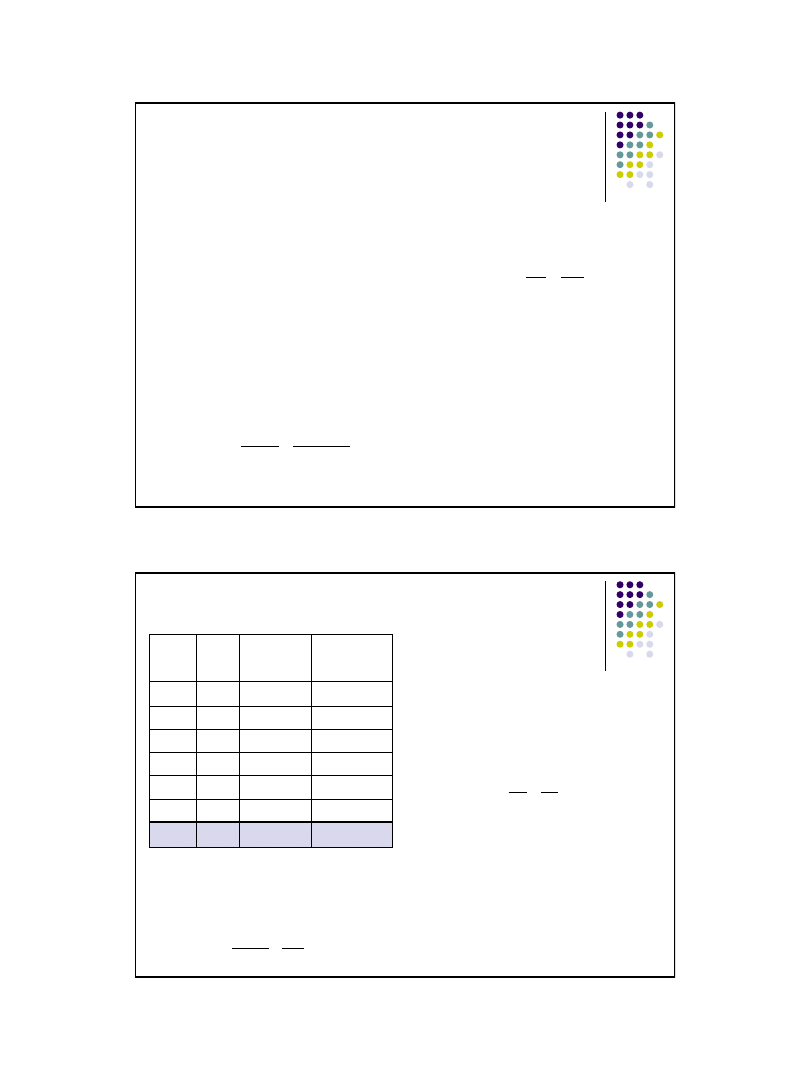
Miary pozycyjne

– przykład

szereg rozdzielczy punktowy

numer

klasy

liczba

osób

liczba

przypadków

licznaość

skumulowana

i

x

i

f

i

f

i_kum

1

0

15

15

2

1

25

40

3

2

6

46

4

3

3

49

5

4

1

50

suma



50



Rozstęp



Współczynnik zmienności
(pozycyjny):



Przedział typowych wartości
cechy (pozycyjny):

Odchylenie ćwiartkowe:
Q

1

= 0

Q

2

(Me) = 1

Q

3

= 1

5

,

0

1

5

,

0







e

Q

M

Q

V

5

,

0

2

0

1

2

1

3











Q

Q

Q

4

0

4

min

max











x

x

R

5

,

1

5

,

0

5

,

0

1

5

,

0

1





















typ

typ

e

typ

e

x

x

Q

M

x

Q

M

2013-03-06

18

35

Miary pozycyjne

– przykład

szereg rozdzielczy przedziałowy



Rozstęp

Przedział

liczba

pracown.

x

i

f

i_sk

w

i

w

i_sk

Q

0,5

5,5

20

3

20

0,1

0,1

5,5

10,5

30

8

50

0,15

0,25

Q1

10,5 15,5

60

13

110

0,3

0,55

Me

15,5 20,5

70

18

180

0,35

0,9

Q3

20,5 25,5

20

23

200

0,1

1,0

suma

200

1,0



Odchylenie ćwiartkowe:



Q

1

= 10,5



Q

2

(Me) = 15,33



Q

3

= 18,357

93

,

3

2

5

,

10

36

,

18

2

1

3











Q

Q

Q







min

max

x

x

R

=25,5-0,5=25



Współczynnik zmienności
(pozycyjny):



Przedział typowych wartości
cechy (pozycyjny):

38

,

0

33

,

10

93

,

3







e

Q

M

Q

V

26

,

19

40

,

11

93

,

3

33

,

15

93

,

3

33

,

15





















typ

typ

e

typ

e

x

x

Q

M

x

Q

M

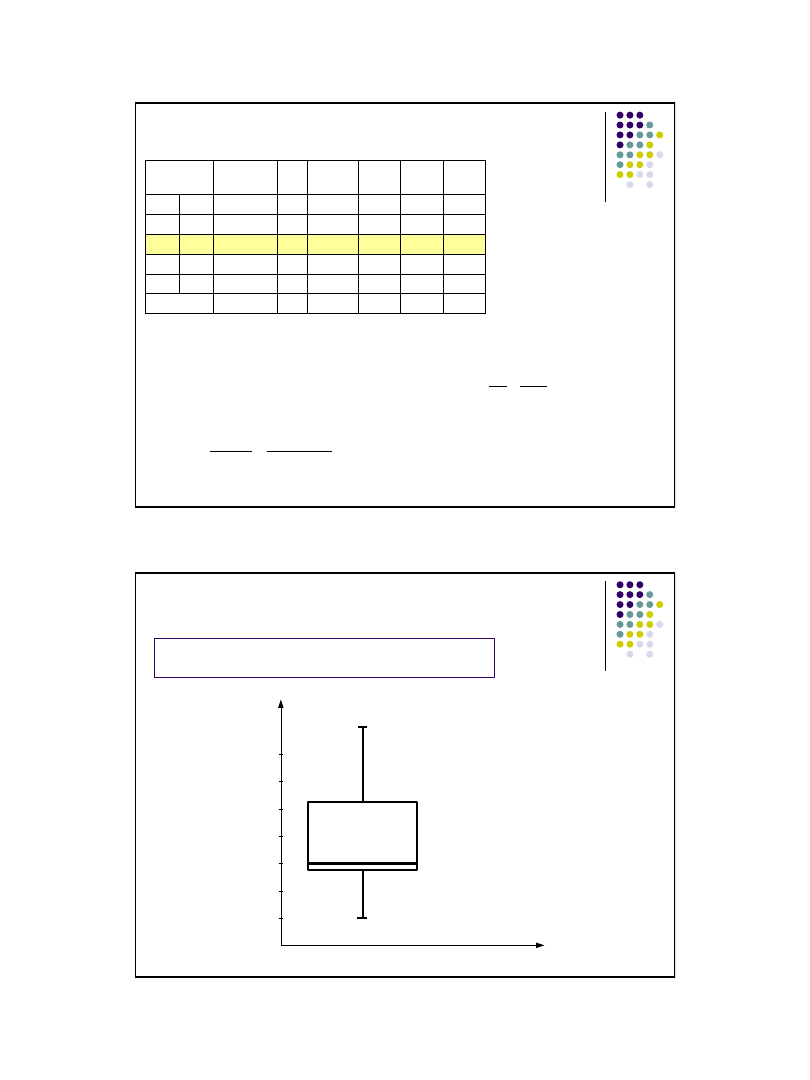
36

Wykres pudełkowy (box-and-whisker-plot)

Liczba osób w kolejce do kasy biletowej

x

i

= 1,2,2,3,3,3,3,5,5,6,7,8

1

8

7

6

5

4

3

2

x

min

= Q

0

= 1

x

max

= Q

4

= 8

Q

3

= 5,25

Q

2

= Me = 3

Q

1

= 2,75

2013-03-06

19

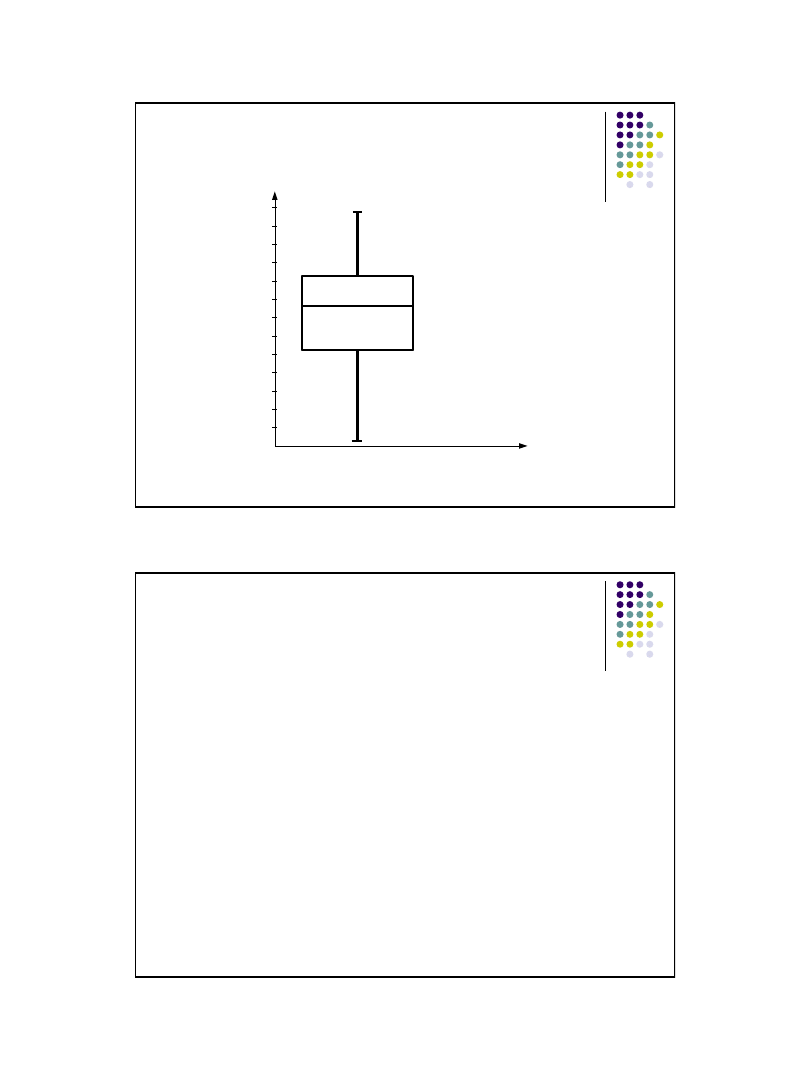
37

Wykres pudełkowy (box-and-whisker-plot)

szereg rozdzielczy przedziałowy

x

min

= Q

0

= 0,5

x

max

= Q

4

= 25,5

Q

3

= 18,4

Q

2

= Me = 15,3

Q

1

= 10,5

2

22

18

14

10

6

26

38

Excel

– funkcje – miary zmienności



=

MAX(liczba1; liczba2; ..)



=MIN(liczba1; liczba2; ..)



=ODCH.STANDARDOWE(liczba1; liczba2; ..)



=ODCH.ŚREDNIE(liczba1; liczba2; ..)



=WARIANCJA(liczba1; liczba2; ..)



SUMA(zakres)



SUMA.ILOCZYNÓW(zakres1;zakres2)



SUMA.KWADRATÓW(zakres1;zakres2)