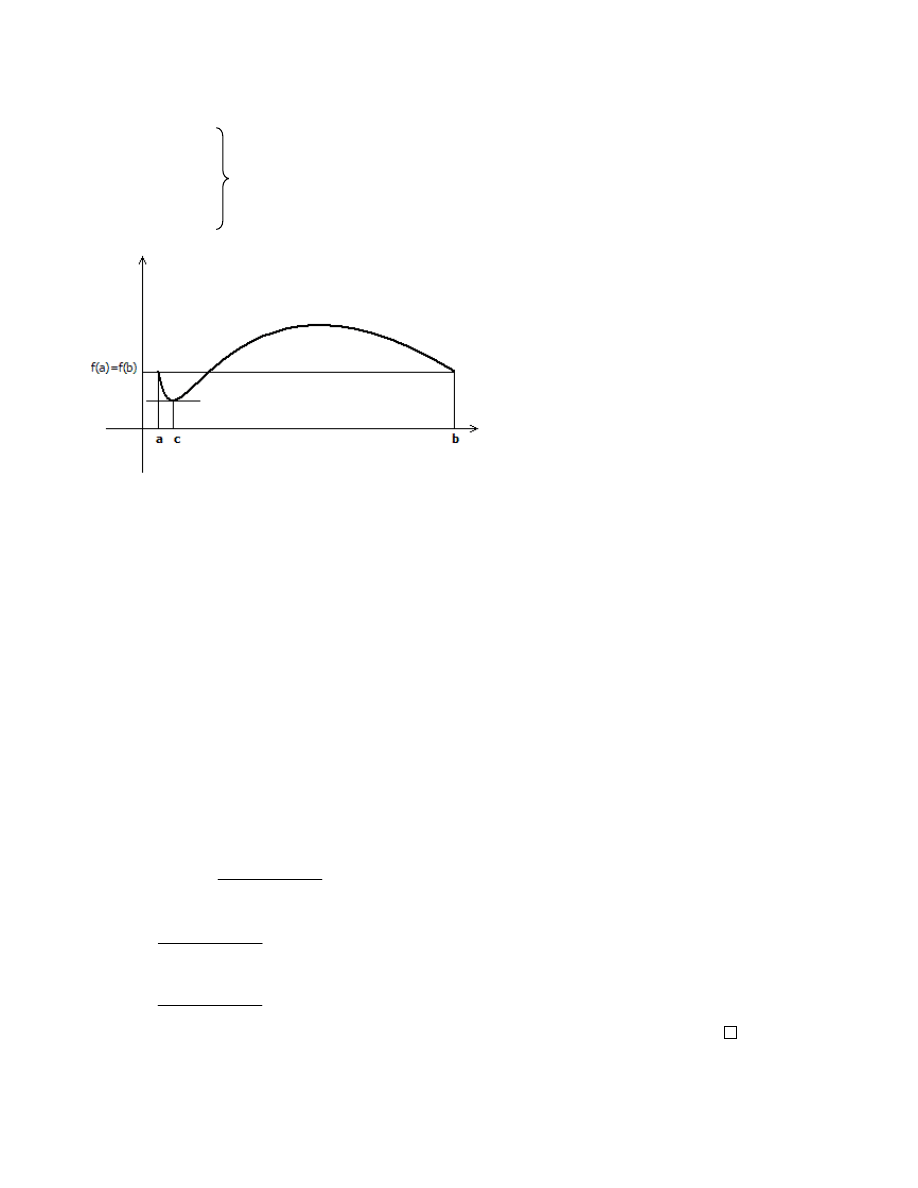
1

Twierdzenie Rolle’a

[ ]

(

)

( )

(

)

( ) ( )

b

f

a

f

b

a

D

f

b

a

C

f

=

∈

∈

,

,

Dowód twierdzenia Rolle’a

z twierdzenia Weierstrass’a (o osi ganiu kresów) mamy

[ ]

(

)

[ ]

( )

[ ]

[ ]

( )

[ ]

[

]

=

=

∈

∃

∈

b

a

f

x

f

b

a

f

x

f

b

a

x

x

b

a

C

f

,

sup

,

inf

:

,

,

,

2

1

2

1

co inaczej mo na zapisa jako

[ ]

(

)

[ ]

( ) ( ) ( )

2

1

,

,

x

f

x

f

x

f

b

a

C

f

b

a

x

≤

≤

∀

∈

∈

rozwa my teraz dwa przypadki
I.

( ) ( )

0

2

1

≡

′

≡

=

f

const

f

x

f

x

f

II.

( ) ( )

( )

( )

b

a

x

b

a

x

x

f

x

f

,

,

2

1

2

1

∈

∨

∈

<

nie stracimy na ogólno ci je li zało ymy, e

( )

b

a

x

,

1

∈

wiemy, e

( )

(

)

b

a

D

f

,

∈

wynika z tego, e

( )

1

x

f ′

∃

( )

( ) ( )

( ) ( )

( ) ( )

( )

( )

0

0

lim

0

lim

lim

1

1

1

1

1

1

1

1

1

1

1

=

′

≤

−

−

≥

−

−

−

−

=

′

′

∃

→

→

→

−

+

x

f

x

x

x

f

x

f

x

x

x

f

x

f

x

x

x

f

x

f

x

f

x

f

x

x

x

x

x

x

( ) ( )

0

:

,

=

′

∈

∃

c

f

b

a

c

2

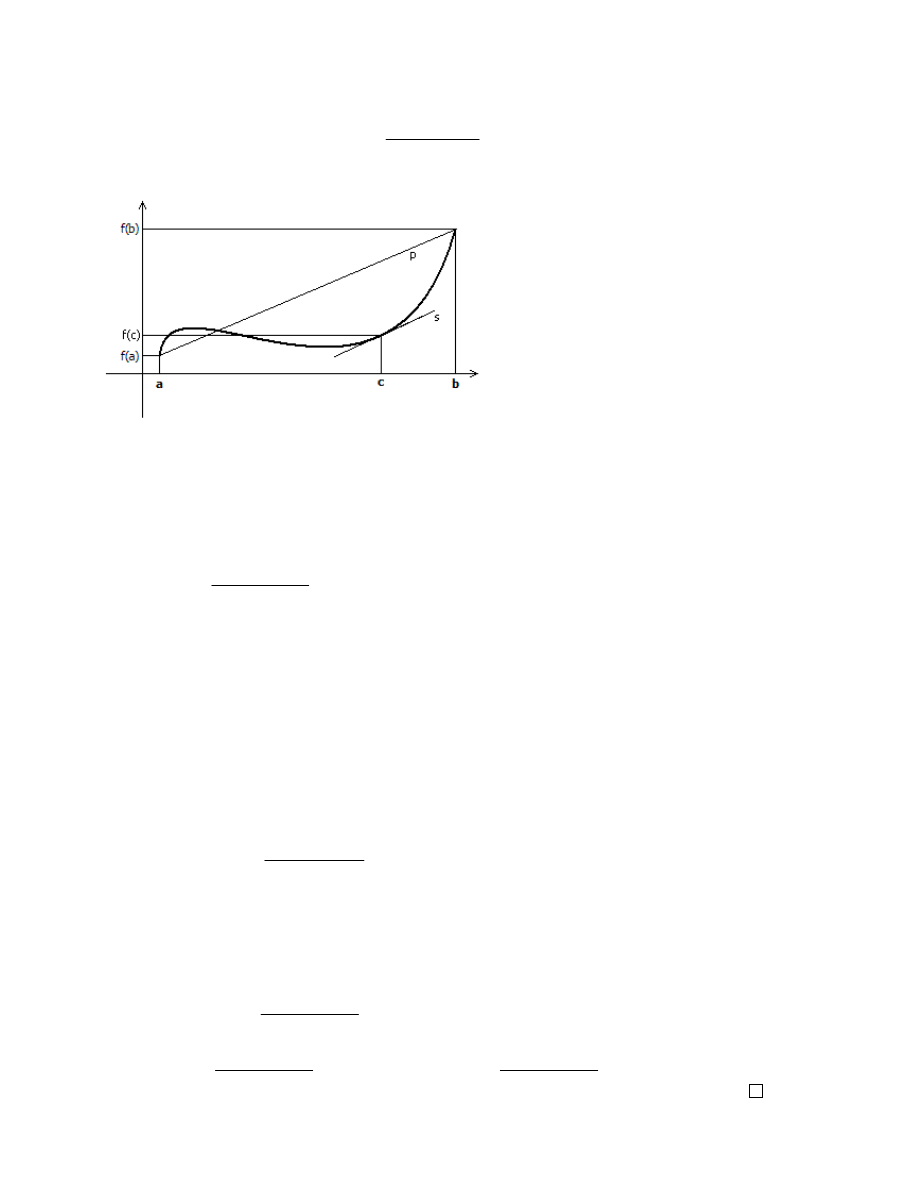
Twierdzenie o warto ci redniej (twierdzenie Lagrange’a)

[ ]

(

)

( )

(

)

( ) ( )

( ) ( )

a

b

a

f

b

f

c

f

b

a

c

b

a

D

f

b

a

C

f

−

−

=

′

∈

∃

∈

∈

:

,

,

,

Prosta

s

to styczna do wykresu funkcji w punkcie styczno ci

c

, a prosta

p

ł czy ze sob punkty

( )

(

)

a

f

a,

oraz

( )

(

)

b

f

b,

.

Wtedy obie proste wyra aj si nast puj cymi wzorami

( ) ( ) ( )(

)

( )

( )(

)

c

x

c

f

c

f

y

s

a

x

a

b

a

f

b

f

a

f

y

p

−

′

+

=

−

−

−

+

=

:

:

Z tw. Lagrange’a wynika, e

s

II

p

.

Dowód twierdzenia Lagrange’a

W celu ułatwienia dowodu, tworzymy funkcj

ϕ

, która b dzie nawi zywała do sytuacji

poprzedniej (twierdzenia Rolle’a).

( )

( ) ( ) ( ) ( )(

)

[ ]

(

)

( )

(

)

( ) ( ) ( )

( ) ( ) ( )

( ) ( )

(

)

( ) ( )

0

:

,

0

0

,

,

:

'

.

=

′

∈

∃

=

−

−

−

=

=

−

=

∈

∧

∈

−

−

−

−

−

=

c

b

a

c

a

f

b

f

a

f

b

f

b

a

f

a

f

a

b

a

D

b

a

C

a

t

a

b

a

f

b

f

a

f

t

f

t

a

Rolle

tw

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

( )

( )

( ) ( ) ( )

( )

( ) ( ) ( )

( )

( )

( ) ( )

a

b

a

f

b

f

c

f

c

a

b

a

f

b

f

c

f

c

a

b

a

f

b

f

t

f

t

b

a

t

−

−

=

′

=

′

∧

−

−

−

′

=

′

−

−

−

′

=

′

∀

∈

0

,

ϕ

ϕ

ϕ

3

Zapiszmy w innej postaci wzór Lagrange’a

( ) ( )

( )(

)

a

b

c

f

a

f

b

f

−

′

+

=

( )

( )

(

)

a

b

a

c

b

a

c

−

+

=

∈

∃

∈

θ

θ

:

1

,

0

,

przyjmijmy, e

=

=

b

x

a

x

:

:

0

wtedy:

( )

(

)

( )

1

,

0

,

0

0

0

∈

∧

−

+

=

∈

θ

θ

x

x

x

c

x

x

c

ów wzór Lagrange’a przyjmuje posta :

( ) ( )

(

)

(

)

[

]

(

)

( )

1

,

0

0

0

0

0

∈

∧

−

−

+

′

+

=

θ

θ

x

x

x

x

x

f

x

f

x

f

je li

0

x

x

≤

to z twierdzenia Lagrange’a mamy:

(

) ( )

( ) ( )

( ) ( )

0

0

0

0

0

:

,

x

x

x

f

x

f

x

x

x

f

x

f

c

f

x

x

c

−

−

=

−

−

=

′

∈

∃

wynika z tego, e nie ma znaczenia czy rozwa amy przedział

[

]

x

x ,

0

czy

[

]

0

, x

x

; wzór pozostaje ten

sam.

Wniosek (o monotoniczno ci funkcji)

Niech

( )

(

)

b

a

D

f

,

∈

, wtedy:

(1)

f

f

⇔

≥

′ 0

jest rosn ca

(2)

f

f

>

′ 0

jest silnie rosn ca

(3)

const

f

f

=

⇔

=

′ 0

Dowód
Ad (1).

( )

Niech

( )

b

a

y

x

,

,

∈

,

y

x

<

.

Wtedy na podstawie tw. Lagrange’a:

( ) ( ) ( )

( )

0

:

,

≥

′

=

−

−

∈

∃

c

f

x

y

x

f

y

f

y

x

c

,

czyli:

( ) ( )

x

f

y

f

≥

,

( )

⇐

( ) ( )

x

f

y

f

≥

, gdy

( )

( ) ( )

0

lim

≥

−

−

=

′

>

+

→

x

y

x

f

y

f

x

f

x

y

x

y

.

Ad (2). Analogicznie jak dowód implikacji

( )

w (1).

4

Ad (3). Z (1) wynika, e funkcje

f

i

-f

s rosn ce, czyli

f

jest rosn ca i malej ca, wi c jest

stała.

Uwaga

Wniosek ten zachodzi, gdy dziedzina funkcji jest przedziałem.

Przykład
Niech

( )

tgx

x

f

=

. Wtedy

( )

0

cos

1

:

2

>

=

′

∈

∀

x

x

f

D

x

f

,

a jednak:

( ) ( )

π

π

4

1

4

3

f

f

<

funkcja

f

nie jest rosn ca.

Jest ona rosn ca jedynie w ka dym z przedziałów

+

+

−

π

π

π

π

k

k

2

,

2

,

Z

k

∈

tworz cych dziedzin .

Uwaga

Implikacji (2) w powy szym wniosku nie mo na odwróci .

Przykład
Funkcja

( )

3

x

x

f

=

jest silnie rosn ca, bo

( ) ( )

2

1

,

,

2

1

2

1

x

f

x

f

x

x

D

x

x

<

∀

<

∈

jednak

( )

0

:

=

′

∈

∃

x

f

D

x

f

z czego wynika, e implikacji (2) nie mo emy odwróci .

Twierdzenie Cauchy’ego (o przyrostach)

[ ]

(

)

( )

(

)

( )

( )

( ) ( ) ( )

( ) ( )

( )

( )

c

g

c

f

a

g

b

g

a

f

b

f

b

a

c

x

g

b

a

D

g

f

b

a

C

g

f

b

a

x

′

′

=

−

−

∈

∃

≠

′

∀

∈

∧

∈

∈

:

,

0

,

,

,

,

,

Dowód

( ) ( )

( )

( ) ( ) ( ) ( )

( ) ( ) ( ) ( )

(

)

[ ]

(

)

( )

(

)

( )

( )

( ) ( )

( )

( ) ( ) ( )

( ) ( ) ( )

( )

( )

( ) ( )

( ) ( )

a

g

b

g

a

f

b

f

c

g

c

f

x

g

a

g

b

g

a

f

b

f

x

f

x

c

b

a

c

b

a

b

a

D

b

a

C

a

g

x

g

a

g

b

g

a

f

b

f

a

f

x

f

t

a

g

b

g

g

a

Rolle

tw

a

Rolle

tw

−

−

=

′

′

′

−

−

−

′

=

′

=

′

∈

∃

=

=

∈

∈

−

−

−

−

−

=

≠

≠

′

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

0

:

,

0

,

,

,

:

0

'

.

'

.

5

Uwaga

[ ]

=

b

a

Id

g

,

wzór Cauchy’ego sprowadza si do wzoru Lagrange’a

opracował Paweł Sztur