11
2. OBIEGI CIEPLNE SILNIKÓW SPALINOWYCH
2.1. Obieg teoretyczny
Obiegi teoretyczne i porównawcze słu do wzgl dnej oceny rzeczywistych procesów termodynamicznych
i analizy ich przebiegu. W obiegach teoretycznych czynnikiem roboczym jest gaz doskonały, co pozwala na
porównanie rzeczywistych przebiegów zachodz cych w silniku z zało eniami, według których silnik powinien
pracowa . Obiegi teoretyczne rozpatruje si przy nast puj cych zało eniach:
- masa czynnika w cylindrze w czasie obiegu jest stała,
- spr anie i rozpr anie odbywa si izentropowo,
- ciepło zostaje dostarczone do czynnika przez izochoryczne (V= const) lub izobaryczne (p = const)
podgrzewanie i odprowadzane jest przez izochoryczne ozi bianie, przy czym skład chemiczny czynnika
nie ulega zmianie,
- ciepła wła ciwe przy stałym ci nieniu i stałej obj to ci dla czynnika podlegaj cego przemianie pozostaj
stałe,
- przemiany termodynamiczne obiegu teoretycznego odbywaj si dostatecznie wolno, natomiast pr dko ci
czynnika w czasie przemiany s równe zeru i nie wyst puj straty przepływu.
Do oceny przebiegu procesu roboczego w silniku stosuje si nast puj ce obiegi teoretyczne:
- z doprowadzeniem ciepła przy stałej obj to ci - obieg Otto,
- z doprowadzeniem ciepła przy stałym ci nieniu - obieg Diesla,
- z doprowadzeniem ciepła przy stałej obj to ci i stałym ci nieniu - obieg Sabathe.
Odprowadzanie ciepła w tych obiegach odbywa si przy stałej obj to ci (V= const).
Warunkami ograniczaj cymi parametry termodynamiczne obiegu s :
- ci nienie otoczenia (przeci tnie około l bar),
- temperatura otoczenia (przeci tnie 290 K),
- najwy sze dopuszczalne ci nienie spalania,
- najwy sza dopuszczalna temperatura spalania.
Obiegiem o najwy szej sprawno ci teoretycznej jest obieg Carnota, który składa si z dwóch izentrop (spr anie
i rozpr anie) oraz dwóch izoterm (odprowadzanie i doprowadzanie ciepła). Sprawno tego obiegu ogranicza
maksymalna i minimalna temperatura czynnika roboczego.
2.1.1. Obieg z doprowadzaniem ciepła przy stałej obj to ci
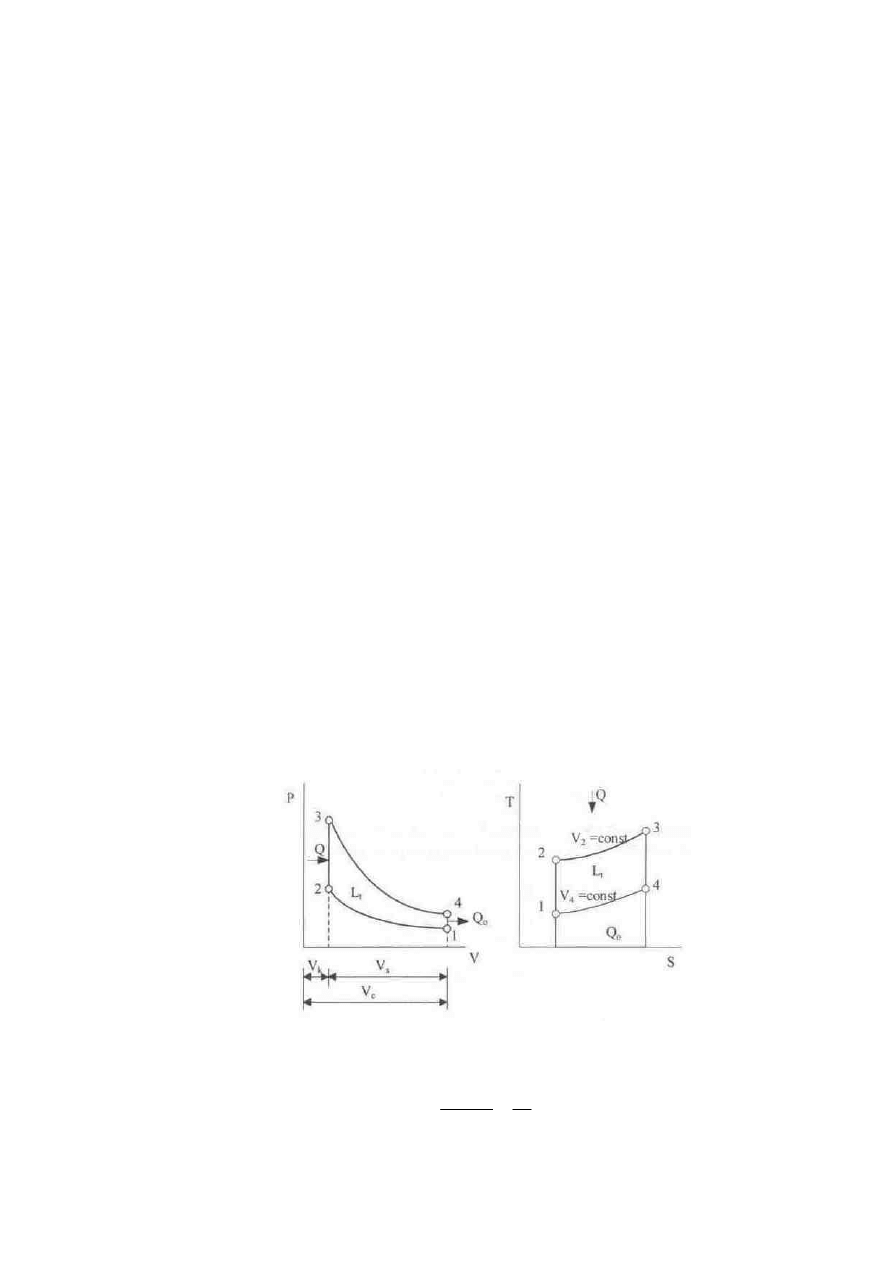
Obieg z doprowadzeniem ciepła przy stałej obj to ci (obieg Otto) przedstawiono na rysunku 2.1. Spr anie
w tym obiegu odbywa si izentropowo (S = const), a doprowadzanie ciepła izochorycznie (V= const), natomiast
rozpr anie - izentropowo (S = const), odprowadzanie za ciepła izochorycznie (V= const).
Rys. 2.1. Obieg teoretyczny z doprowadzaniem ciepła przy V = const
Wykorzystanie energii cieplnej okre la współczynnik sprawno ci teoretycznej obiegu:
Q
L
Q
Q
Q
t
t
=
−
=
0
η
(2.1)
12
Ciepło doprowadzone przy stałej obj to ci wynosi:
(
)
2
3
T
T
c
Q
v
−
=
(2.2)
Ciepło odprowadzone przy stałej obj to ci wynosi:
(
)
1
4
0
T
T
c
Q
v
−
=
(2.3)
Po podstawieniu otrzymuje si :
(
)
(
)
(
)
2
3
1
4
2
3
T
T
c
T
T
c
T
T
c
v
v
v
t
−
−
−
−
=
η
(2.4)
Stopie spr ania okre la stosunek całkowitej obj to ci cylindra do obj to ci komory spalania:
k
k
s
k
c
V
V
V
V
V
V
V
V
V
+
=
=
=
=
2
1
3
4
ε
(2 5)
Temperatury czynnika w punktach l i 2 oraz 3 i 4 le cych na izentropach mo na przedstawi jako funkcje
stopnia spr ania (ε):
1
1
1
2
−
−
=
=
κ
κ
ε
k
c
V
V
T
T
(2.6a)
1
1
4
3
−
−
=
=
κ
κ
ε
k
c
V
V
T
T
(2.6b)
Uwzgl dniaj c zale no ci:
3
1
3
4
T
T
T
T
=
(2.7a)
3
1
4
1
T
T
T
T
=
(2.7b)
wyra enie na sprawno teoretyczn przyj mi posta :
κ
κ
ε
ε
η
−
−
−
=
−
=
−
=
1
1
2
1
1
1
1
1
T
T
t
(2.8)
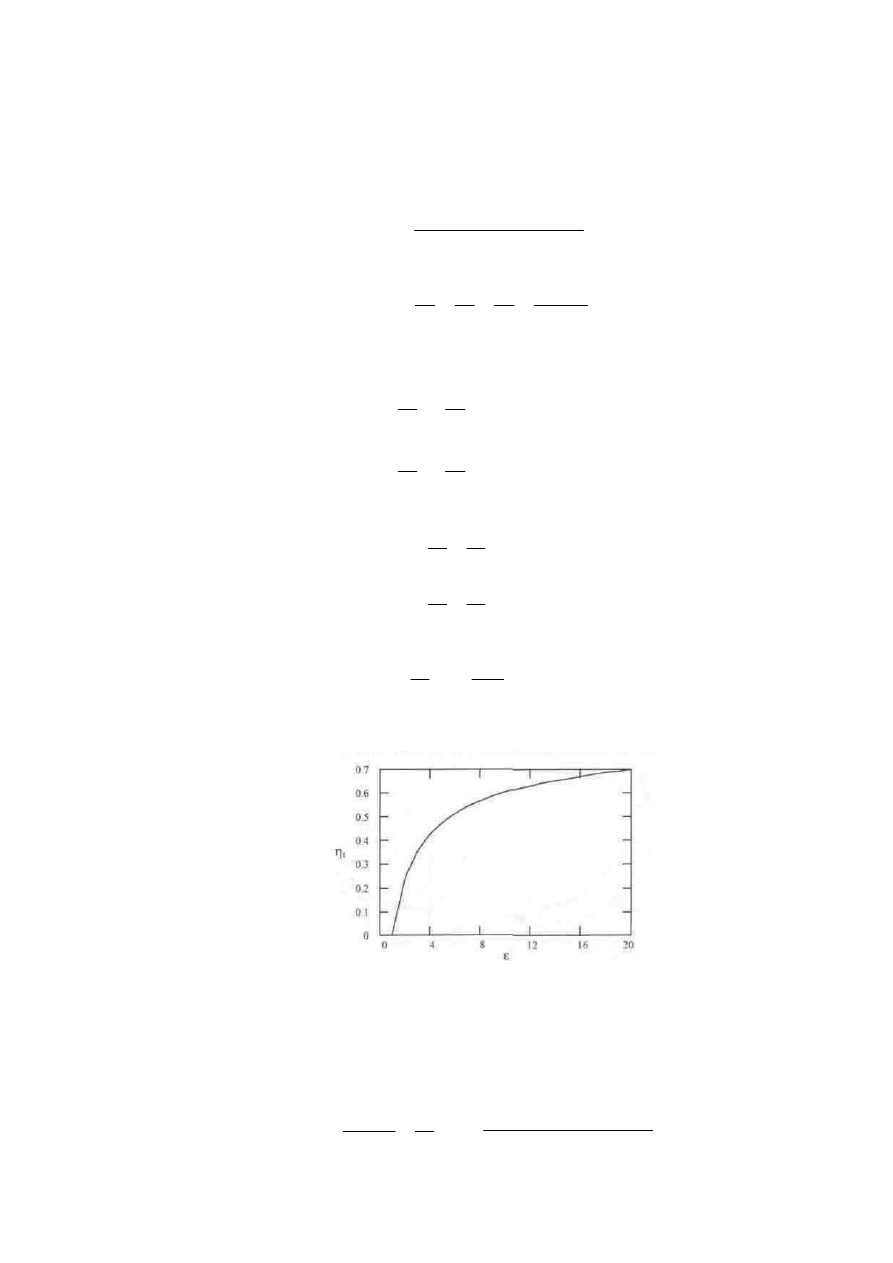
Z wyra enia (2.8) wynika, e warto współczynnika sprawno ci teoretycznej ro nie w miar wzrostu stopnia
spr ania (ε) (rys.2.2).
Rys.2.2. Współczynnik sprawno ci teoretycznej obiegu Otto w funkcji stopnia spr ania (ε) dla κ = 1,4
2.1.2. Obieg z doprowadzaniem ciepła przy stałym ci nieniu
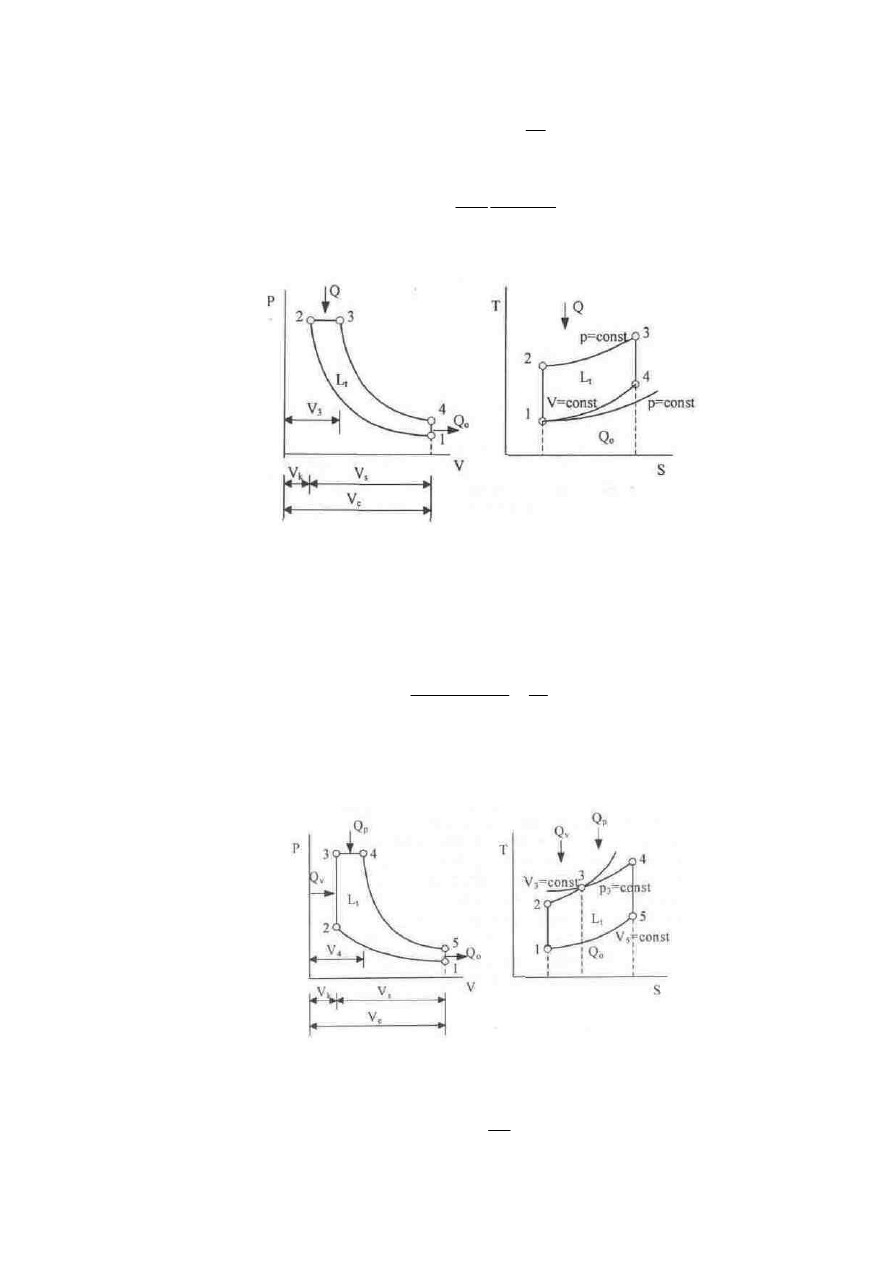
Obieg z doprowadzaniem ciepła przy stałym ci nieniu (Diesel) składa si z nast puj cych przemian:
izentropowego spr ania i rozpr ania, izobarycznego doprowadzania ciepła i izochorycznego odprowadzania
ciepła (rys. 2.3). Sprawno teoretyczna obiegu wynosi:
Q
L
Q
Q
Q
t
t
=
−
=
0
η
=
(
)
(
)
(
)
2
3
1
4
2
3
T
T
c
T
T
c
T
T
c
v
v
v
t
−
−
−
−
=
η
(2.9)
13
Wprowadzaj c definicj stopnia izobarycznego przyrostu obj to ci w postaci:
2
3
V
V
v
=
ϕ
(2.10)
wyra enie (2.9), po przekształceniach, przyjmie posta :
(
)
1
1
1
1
1
−
−
−
=
−
v
v
t
ϕ
κ
ϕ
ε
η
κ
κ
(2.1l)
Z wyra enia (2.11) wynika, e w miar wzrostu stopnia przyrostu obj to ci ((pv) sprawno teoretyczna obiegu
Diesla maleje.
Rys. 2.3. Obieg teoretyczny z doprowadzaniem ciepła przy stałym ci nieniu
2.1.3. Obieg z doprowadzaniem ciepła przy stałej obj to ci i stałym ci nieniu
Obieg z doprowadzaniem ciepła przy stałej obj to ci i stałym ci nieniu (Sabathe) jest obiegiem, według
którego pracuj współczesne, wysokopr ne silniki spalinowe. Schemat tego obiegu przedstawiono na
rysunku 2.4. Sprawno takiego obiegu mo na przedstawi w postaci:
Q
L
Q
Q
Q
Q
Q
t
p
v
p
v
t
=
+
−
+
=
0
η
(2.12)
Poszczególne udziały ciepła wynosz odpowiednio:
- ciepło doprowadzone przy V= const; Qv = cv (T3 – T2)
- ciepło doprowadzone przy p = const; Qp = cp (
T
4 –T3)
- ciepło odprowadzone przy V= const; Qo = cv (T5 – T1).
Rys. 2.4. Obieg teoretyczny z doprowadzaniem ciepła przy stałej obj to ci i stałym ci nieniu
Po wprowadzeniu definicji izochorycznego przyrostu ci nienia w postaci:
2
3
p
p
v
=
ϕ
(2.13)
14
i uwzgl dniaj c wyra enia
3
1
2
1
V
V
V
V
=
=
ε
oraz
2
4
3
4
V
V
V
V
v
=
=
ϕ
oraz po odpowiednim uporz dkowaniu wszystkich składowych wyra enia (2.12) współczynnik sprawno ci
teoretycznej obiegu Sabathe przyjmie posta :
(
)
(
)
1
1
1
1
1
−
+
−
−
=
−
v
p
v
p
t
ϕ
κϕ
ϕ
ϕ
κ
ε
η
κ
κ
(2.14)
Obieg Sabathe jest najbardziej zbli ony do rzeczywistego przebiegu, wyst puj cego w silnikach
spalinowych rednio- i szybkoobrotowych. W silnikach o zapłonie iskrowym uwidacznia si to na wykresie
indykatorowym poprzez pochylenie izochory. Zjawisko to wyst puje wyra niej w silnikach z zapłonem
samoczynnym, w których spalanie odbywa si zawsze z du ym przyrostem ci nienia.
Z wyra enia (2.14) mo na wyprowadzi odpowiednie wzory na sprawno teoretyczn obiegu Otto i
Diesla. W pierwszym przypadku stopie przyrostu obj to ci ϕv = l, w drugim - stopie przyrostu ci nienia ϕp =
l. Po podstawieniu tych wielko ci do wyra enia (2.14) otrzyma si odpowiednie wzory dla obiegu Otto i Diesla.
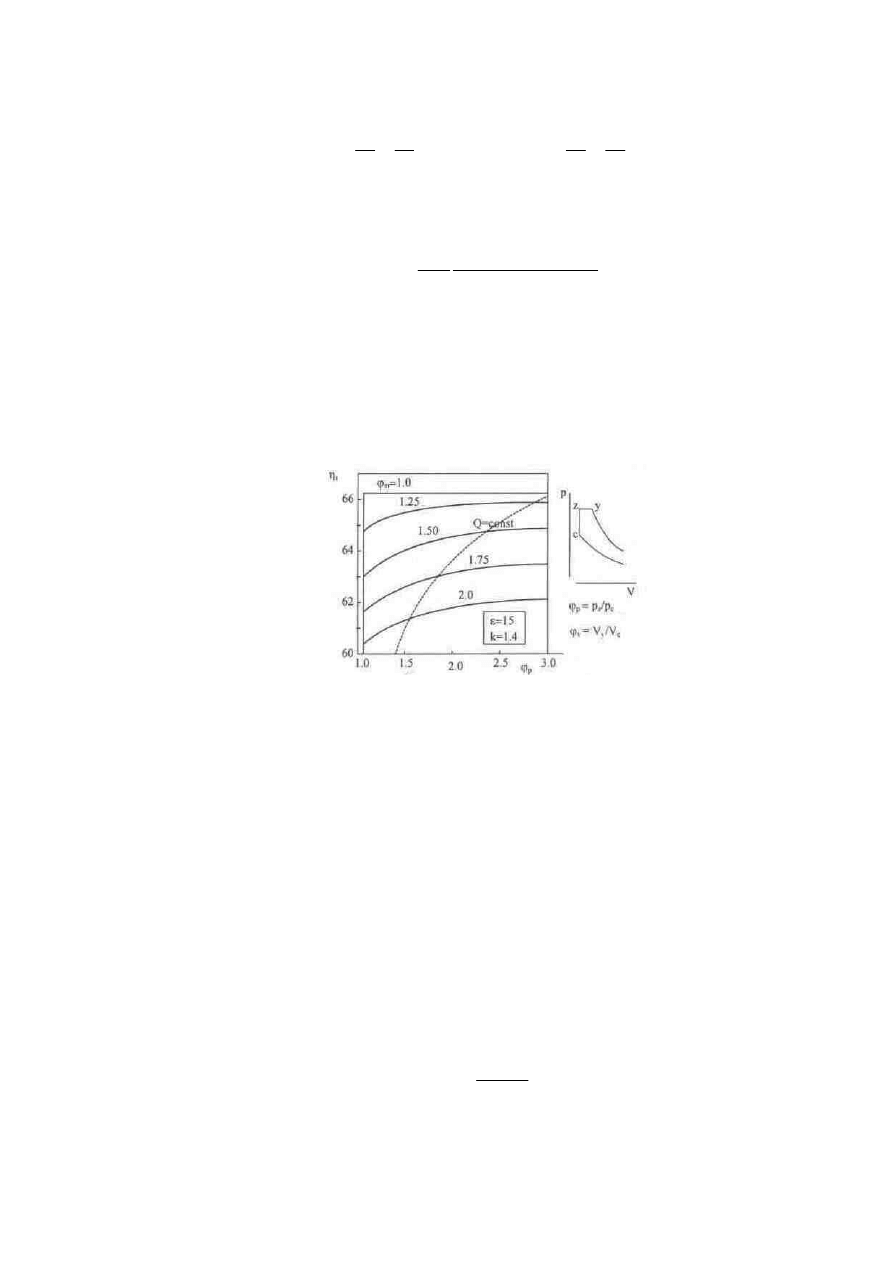
Rys.2.5. Sprawno teoretyczna (iii) obiegu w funkcji izochorycznego przyrostu ci nienia (ϕp) i izobarycznego
przyrostu obj to ci (ϕv) [8]
Sprawno obiegu Sabathe (η) ro nie wraz ze wzrostem stopnia spr ania (ε) i izochorycznego przyrostu
ci nienia (ϕp), natomiast maleje ze wzrostem izobarycznego przyrostu obj to ci (ϕv).
Wpływ współczynników (ϕp) i (ϕv) przedstawiono na rysunku 2.5. Na wykresie zaznaczono krzyw stałej
warto ci ciepła doprowadzonego do obiegu (Q). Zale no pomi dzy tymi współczynnikami okre la stosunek
Qv/Qp. Je eli ciepło doprowadzone przy stałej obj to ci (Qv) ro nie, to ro nie równie współczynnik (ϕp), a
tym samym sprawno obiegu (ηt). Jednocze nie zmniejsza si ilo ciepła doprowadzona przy stałym ci nieniu
(Qp), a wi c zmniejsza si tak e współczynnik (ϕv). Sprawno obiegu (ηt) osi ga warto maksymaln przy
współczynniku ϕv= l.
Wzgl dy wytrzymało ciowe i warunki wła ciwego spalania ograniczaj stopie spr ania (ε) i stopie
izochorycznego przyrostu ci nienia (ϕp) ponad okre lone warto ci. Dla współczesnych silników okr towych
stopie spr ania wynosi ε = 10 do 18.
2.1.4. rednie ci nienie teoretyczne
rednie ci nienie teoretyczne (pi) okre la stosunek pracy teoretycznej (Lt) do przyrostu obj to ci, jaki
wyst puje, gdy dany czynnik wykonuje t prac :
2
1
V
V
L
p
t
t
−
=
(2.5)
Warto
redniego ci nienia teoretycznego zale y od rodzaju obiegu teoretycznego. Podstawiaj c do
wyra enia (2.15) znane ju wyra enia i porz dkuj c je otrzymuje si :
- dla obiegu Otto z doprowadzeniem ciepła przy V = const, gdzie ϕv =l, ϕp> l: