1

PR

ĄD ELEKTRYCZNY

ŁADUNEK ELEKTRYCZNY W

RUCHU

Pr

ąd elektryczny

E=0

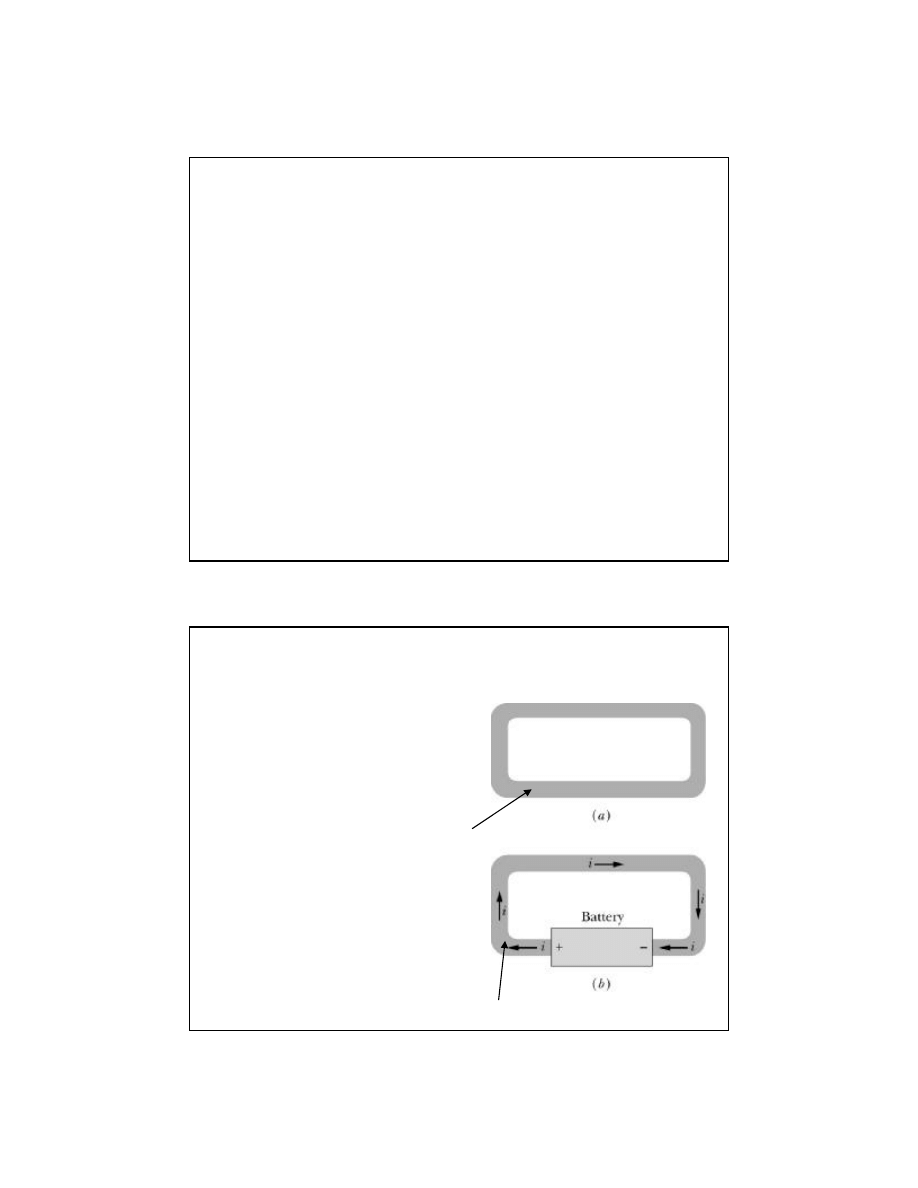
a) Ramka miedziana w równowadze

elektrostatycznej. Ka

żdy punkt ramki

ma taki sam potencja

ł. W każdym punkcie

ramki nat

ężenie pola jest równe zeru

b) Bateria (

źródło) wprowadza różnicę

potencja

łów między biegunami.

Powstaje pole elektryczne w ramce.

Obserwujemy uporz

ądkowany ruch

ładunków – prąd elektryczny

E

≠0

2

Definicja nat

ężenia prądu

• Nat

ężenie prądu jest skalarem

• Jednostk

ą natężenia prądu jest 1A=1C/s

(ale to nie jest definicja tej jednostki!)

• Umownie przyjmuje si

ę, że prąd płynie tak jakby był to

ruch

ładunków dodatnich. W rzeczywistości prąd w

metalu stanowi

ą elektrony przewodnictwa

dt

dq

i

=

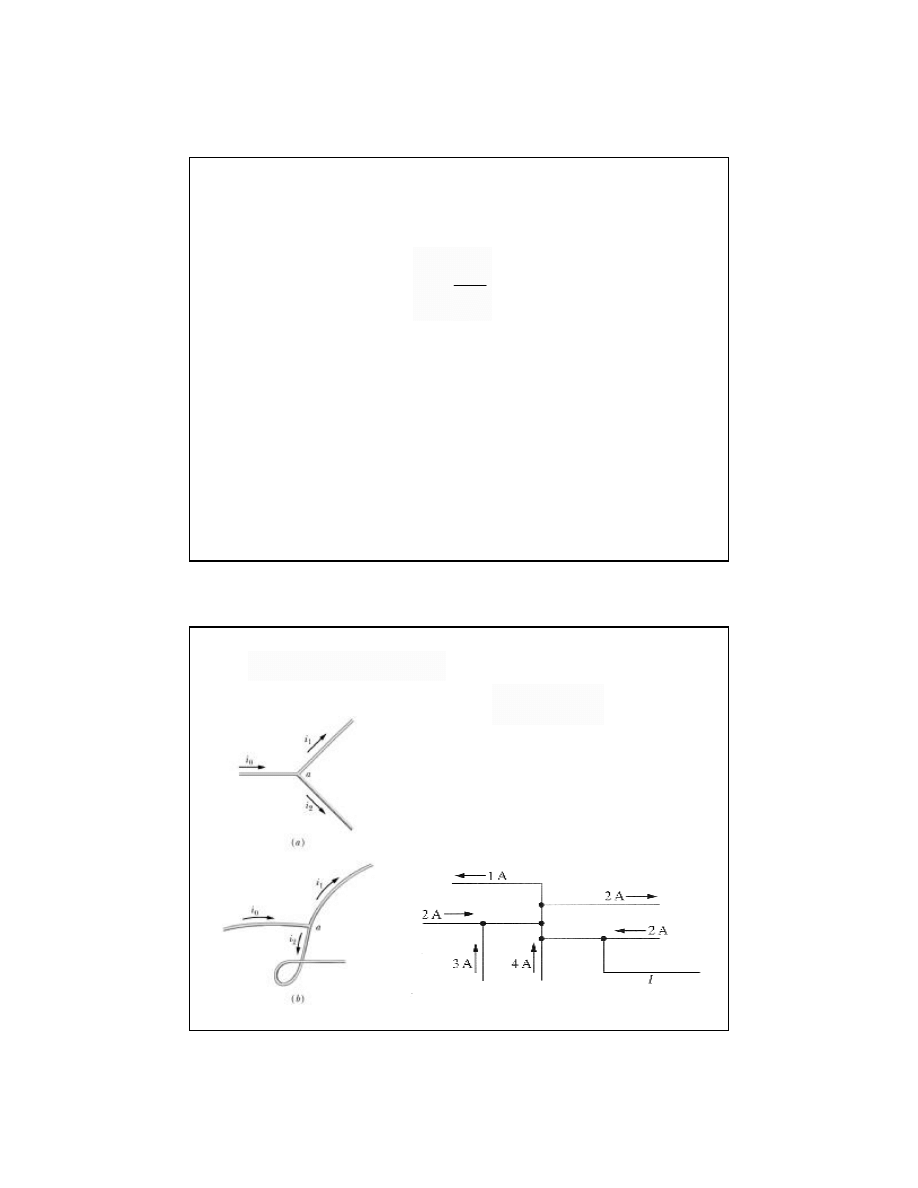
a - węzeł

2

1

o

i

i

i

+

=

I prawo Kirchhoffa

Zadanie domowe-1

Jaka jest wartość prądu I i kierunek
przepływu prądu w dolnym
przewodniku z prawej strony?

3

G

ęstość prądu

• G

ęstość prądu jest to wektor, którego wartość

równa jest nat

ężeniu prądu przepływającemu

przez element pola przekroju powierzchni na
jednostk

ę pola tej powierzchni

S

d

i

d

j

=

S

1

j

1

∫

=

S

j

r

o

r

d

i

Warto

ść natężenia prądu

pozostaje sta

ła, zmienia się

g

ęstość prądu – prawo ciągłości

przep

ływu, zasada zachowania

ładunku

j

2

S

2

strumie

ń

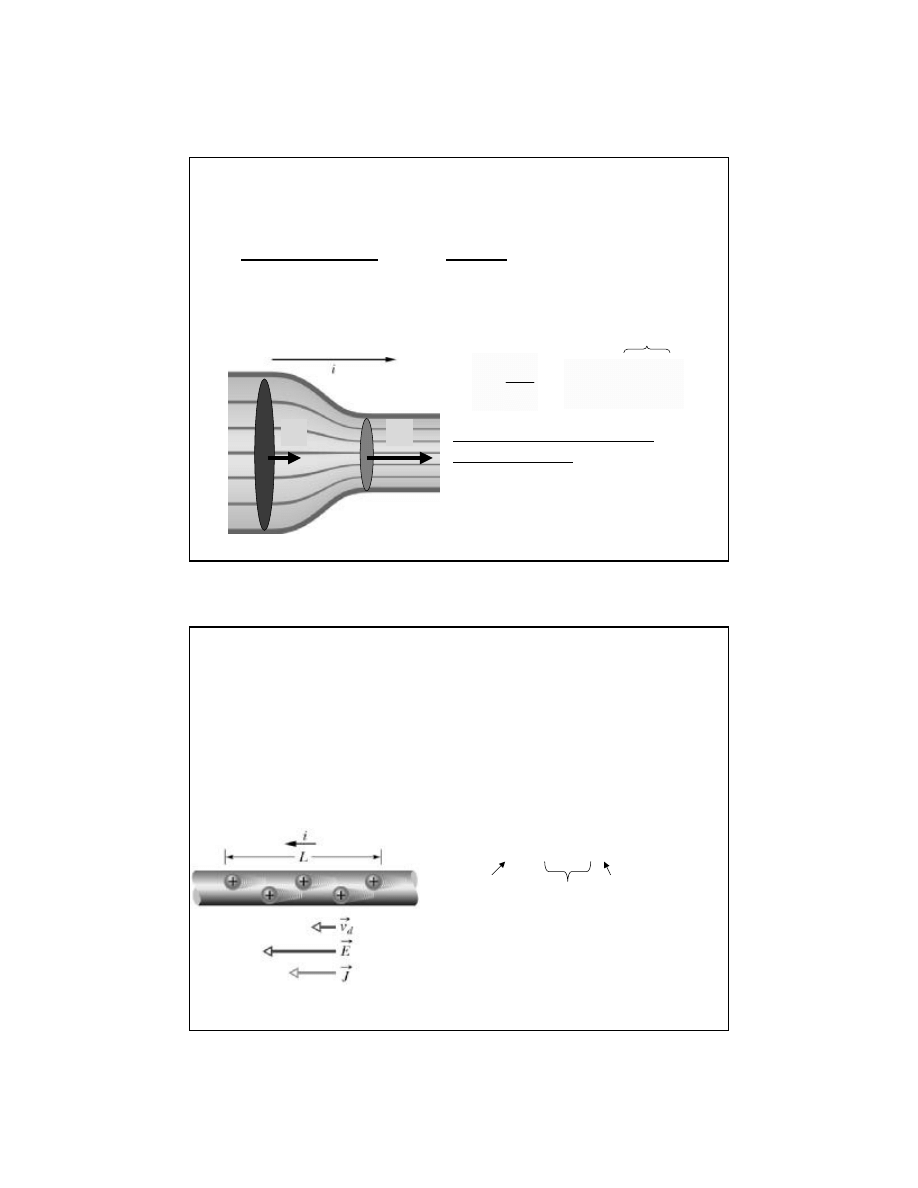
Mechanizm przewodnictwa w

metalach

• Gdy pr

ąd nie płynie, elektrony przewodnictwa poruszają

si

ę chaotycznie z prędkościami ok. 10

6

m/s

• Elektrony w przewodniku poruszaj

ą się w sposób

uporz

ądkowany z prędkością unoszenia v

d

po

przy

łożeniu pola elektrycznego (v

d

=10

-5

-10

-4

m/s)

e

)

nSL

(

q

=

ca

łkowity

ładunek
no

śników

liczba
no

śników

ładunek
elektronu

n – koncentracja no

śników ładunku

(elektronów) czyli ich liczba na jednostk

ę

obj

ętości

4

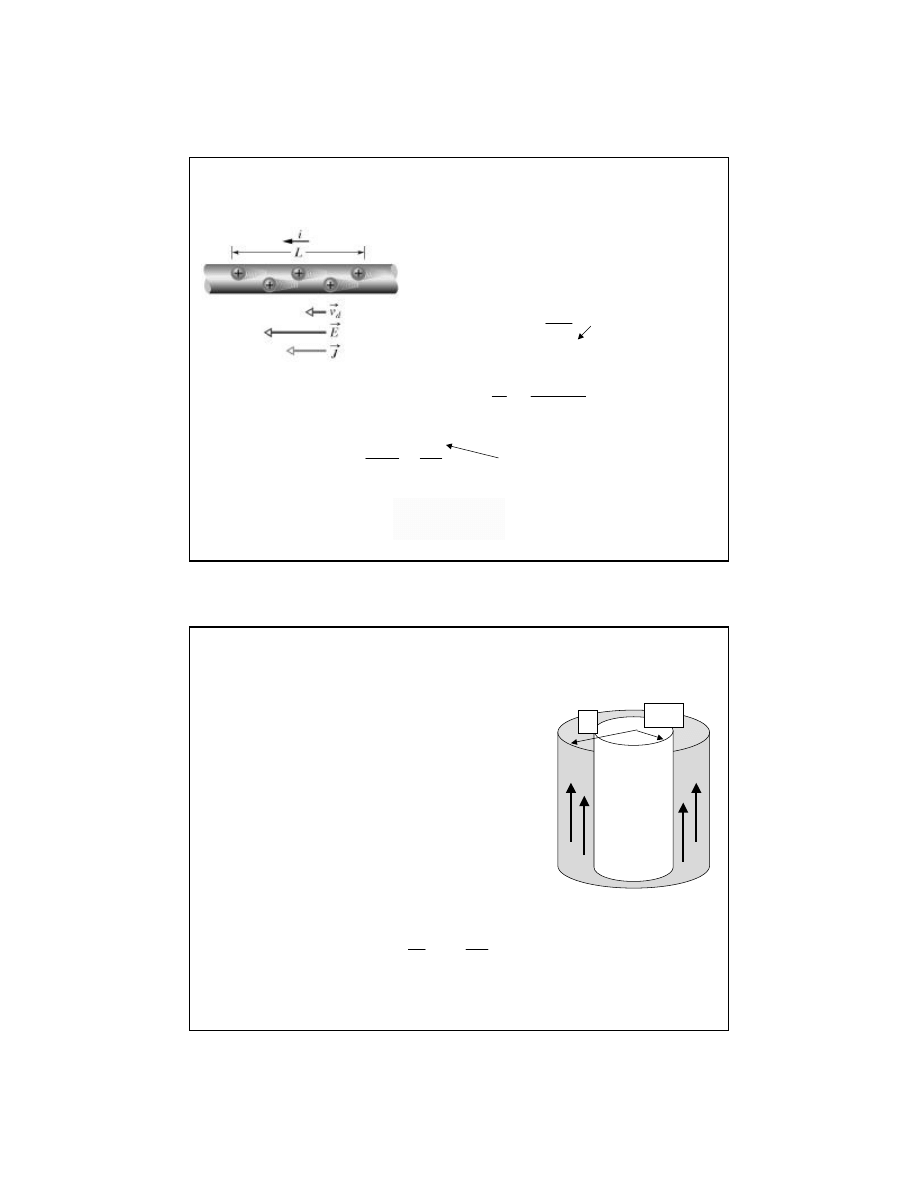
Mechanizm przewodnictwa w

metalach

d

v

L

t

=

czas, w jakim

ładunek przepływa

przez dowolny przekrój
przewodnika

g

ęstość

pr

ądu

pr

ędkość

unoszenia

d

d

nSev

v

/

L

nSLe

t

q

=

=

=

i

nat

ężenie prądu

pr

ędkość

unoszenia

ne

j

nSe

v

d

=

=

i

d

v

j

r

r

)

ne

(

=

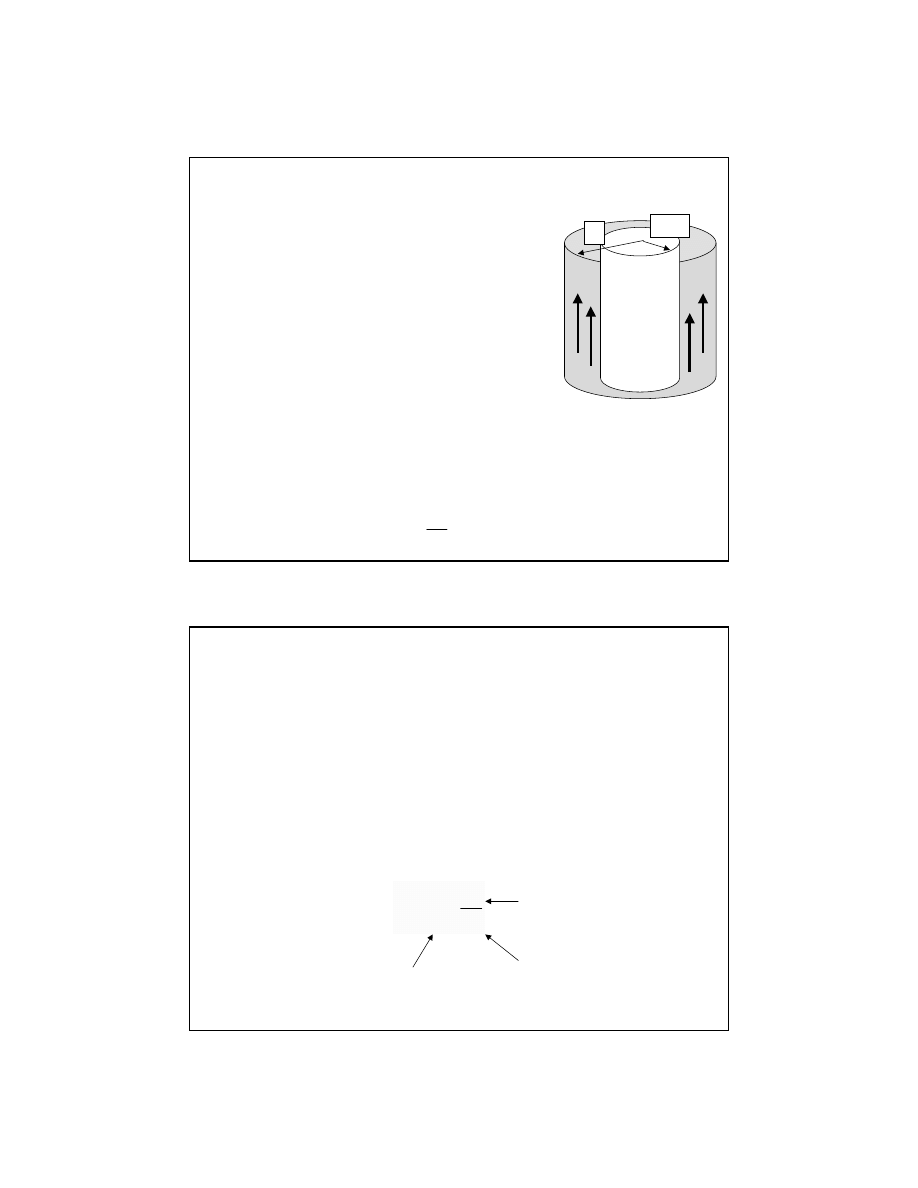
Przyk

ład-1

R/2

R

j

r

G

ęstość prądu w przewodniku o kształcie

walca o promieniu R =2 mm jest
jednakowa na ca

łym przekroju

przewodnika i równa j=2·10

5

A/m

2

. Ile

wynosi nat

ężenie prądu,

przep

ływającego przez zewnętrzną

warstw

ę przewodnika, w obszarze

pomi

ędzy R/2 i R?

Rozwi

ązanie:

'

jS

=

i

bo j=const na ca

łym przekroju walca

2

2

2

R

4

3

2

R

R

'

S

π

=













π

−

π

=

A

9

,

1

=

i

Odpowied

ź:

5

Przyk

ład-2

R/2

R

j

r

Za

łóżmy, że gęstość prądu w przewodniku o

kszta

łcie walca o promieniu R =2 mm nie

jest jednakowa na ca

łym przekroju

przewodnika i zmienia si

ę z odległością r od

środka walca zgodnie ze wzorem j = αr

2

,

gdzie

α= 3·10

11

A/m

4

. Ile wynosi nat

ężenie

pr

ądu, przepływającego przez zewnętrzną

warstw

ę przewodnika, w obszarze pomiędzy

R/2 i R?

Rozwi

ązanie:

A

1

,

7

=

i

Odpowied

ź:

∫

∫

∫

α

=

=

=

R

2

/

R

2

rdr

π

2

r

jdS

dS

j

r

o

r

i

4

R

πα

32

15

=

i

Zadanie domowe-1

Ile wynosi pr

ędkość unoszenia elektronów przewodnictwa w

przewodniku miedzianym o promieniu r = 900

μm, w którym

p

łynie prąd o natężeniu i=17 mA? Przyjąć, że każdy atom

miedzi dostarcza jednego elektronu przewodnictwa, a
g

ęstość prądu jest stała na całym przekroju przewodnika.

Wskazówka:

W pierwszym etapie zadania nale

ży znaleźć koncentrację

elektronów przewodnictwa n stosuj

ąc wzór:

M

N

A

ρ

=

n

liczba Avogadro=liczba atomów w
jednym molu równa 6,02·10

23

mol

-1

g

ęstość, dla Cu równa

8,96 ·10

3

kg/m

3

masa molowa, dla Cu
równa 63,54 ·10

-3

kg/mol

6

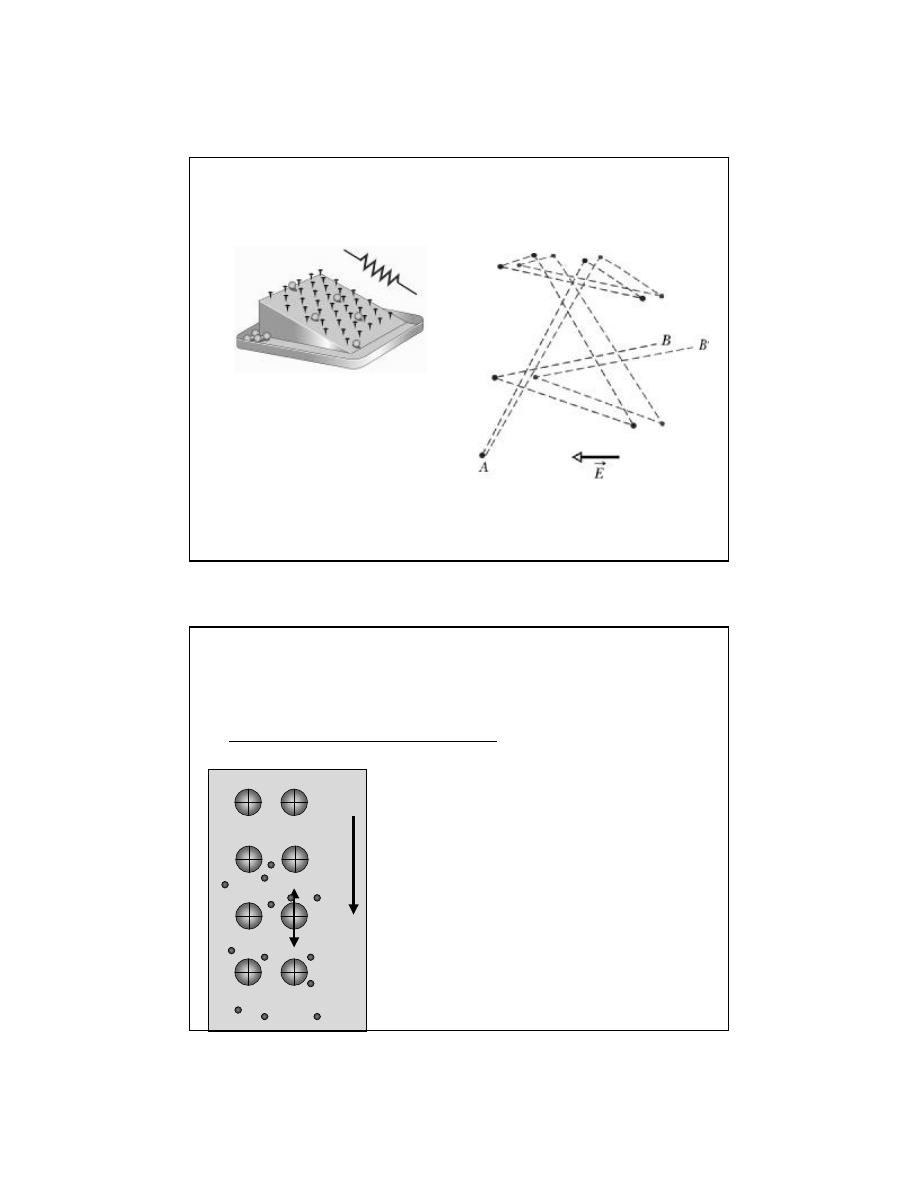
Co to jest rezystancja?

Model mechaniczny rezystancji

R

Model mikroskopowy ruchu elektronu od zderzenia do
zderzenia (linia

łamana od A do B). Ta sama linia AB’

po przy

łożeniu pola elektrycznego (v

d

oko

ło 2 mm/h)

Prawo Ohma – obraz mikroskopowy

Klasyczna teoria elektronowa przewodnictwa w metalu
– model elektronów swobodnych

Za

łożenia:

•elektrony przewodnictwa poruszaj

ą się

swobodnie w ca

łej objętości – „gaz

elektronów swobodnych”

•elektrony zderzaj

ą się tylko z dodatnimi

jonami metalu, a nie z elektronami

•jony metalu w w

ęzłach sieci, drgają wokół

po

łożeń równowagi

e

e

e

e

e

e

e

e

e

e

e

e

e

E

7

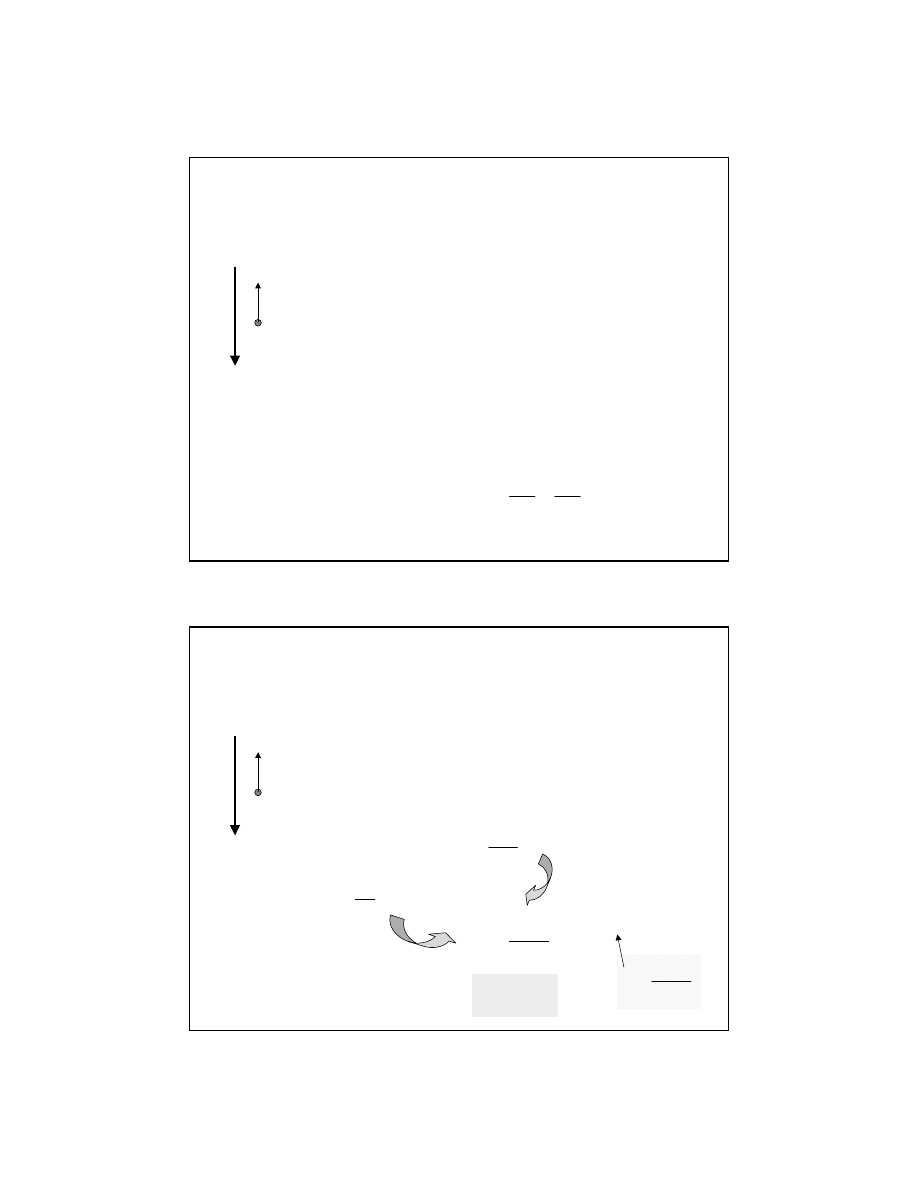
Prawo Ohma – obraz mikroskopowy

Ruch elektronów przewodnictwa w polu
elektrycznym jest z

łożeniem ruchów:

•chaotycznego wynikaj

ącego z

przypadkowych zderze

ń (z jednakową

pr

ędkością „efektywną” pomiędzy

zderzeniami v

eff

≈ 10

6

m/s)

•uporz

ądkowanego, wywołanego polem

Pr

ędkość unoszenia v

d

jest wynikiem oddzia

ływania

pola elektrycznego na elektrony.

E

a

e

e

m

eE

m

F

a

=

=

przyspieszenie jakie uzyskuje
elektron pomi

ędzy zderzeniami

Prawo Ohma – obraz mikroskopowy

ale:

E

a

ne

j

v

d

=

Natura zderze

ń elektronów przewodnictwa jest

taka,

że po kolejnym zderzeniu elektron „traci

pami

ęć” o poprzedniej prędkości unoszenia.

W

średnim czasie między zderzeniami, elektron

uzyska

średnio prędkość unoszenia:

τ

e

d

m

eEτ

τ

a

v

=

=

j

τ

n

e

m

E

2

e

=

j

E

r

r

ρ

=

Prawo Ohma w postaci
mikroskopowej

τ

n

e

m

2

e

=

ρ

rezystywno

ść

lub opór
w

łaściwy

8

Rezystywno

ść a przewodność

• rezystywno

ść ρ jest to stała materiałowa,

zale

ży od rodzaju materiału ale także od

temperatury

• przewodno

ść właściwa (konduktywność) σ

jest odwrotno

ścią rezystywności

)

T

T

(

ρ

ρ

ρ

o

o

o

−

∝

−

μ

en

m

τ

n

e

ρ

1

σ

e

2

=

=

=

ruchliwo

ść nośników ładunku

e

d

m

τ

e

E

v

μ

=

=

T

ρ

ρ

TWR

o

∆

∆

=

temperaturowy wspó

łczynnik oporu

dla metalu

Metale i pó

łprzewodniki

μ

en

σ

=

Wzór

pozwala przeanalizowa

ć zależności

temperaturowe przewodnictwa

W metalu: koncentracja elektronów jest du

ża lecz nie

zale

ży od temperatury, ruchliwość maleje gdy rośnie

temperatura, st

ąd przewodnictwo elektryczne maleje z

temperatur

ą

W pó

łprzewodniku: koncentracja elektronów silnie

zale

ży od temperatury – rośnie ze wzrostem

temperatury, ruchliwo

ść słabo zależy temperatury, stąd

przewodnictwo elektryczne ro

śnie z temperaturą

9

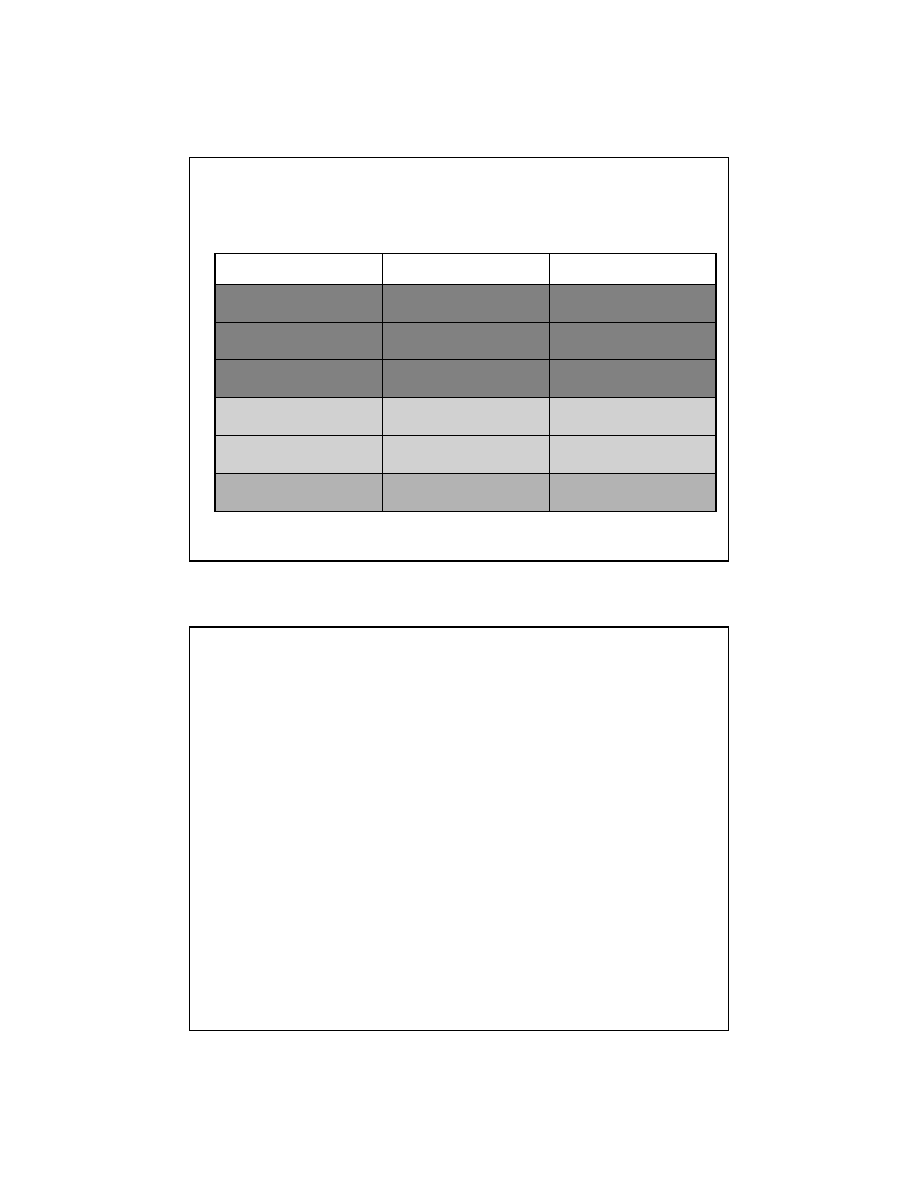
Rezystywno

ść metali,

pó

łprzewodników i izolatorów

10

10

-10

14

Szk

ło

8,7 ·10

-4

Krzem typu n

-70 ·10

-3

2,5 ·10

3

Krzem

0,002 ·10

-3

4,82 ·10

-8

Manganin

4,3 ·10

-3

1,69 ·10

-8

Mied

ź

4,1 ·10

-3

1,62 ·10

-8

Srebro

TWR [K

-1

]

ρ [Ω·m]

Materia

ł

temperatura pokojowa

Zadanie domowe-2

Poszuka

ć danych dotyczących koncentracji i

ruchliwo

ści nośników w typowych metalach i

pó

łprzewodnikach. Na tej podstawie wykonać

tabel

ę podobną do podanej.

10

PRAWO OHMA-cd

• Prawo Ohma wyra

żone w innej postaci (nadal

mikroskopowo)

j

E

r

r

ρ

=

E

j

r

r

σ

=

• Prawo Ohma wyra

żone w postaci makroskopowej

(przy u

życiu wielkości mierzonych)

I

R

U

=

GU

U

R

1

I

=

=

R - rezystancja (opór)

G - konduktancja

jednostk

ą rezystancji jest

1V/A czyli 1

Ω (om)

jednostk

ą konduktancji jest

1S=1

Ω

-1

(simens)

Prawo Ohma brzmi: nat

ężenie prądu,

p

łynącego przez przewodnik jest wprost

proporcjonalne do ró

żnicy potencjałów,

przy

łożonej do przewodnika.

Element obwodu spe

łnia prawo Ohma, gdy jego opór

(rezystancja) nie zale

ży od wartości i polaryzacji przyłożonej

ró

żnicy potencjałów.

Materia

ł przewodzący spełnia prawo Ohma, gdy jego opór

w

łaściwy (rezystywność) materiału nie zależy od wartości i

kierunku przy

łożonego pola elektrycznego.

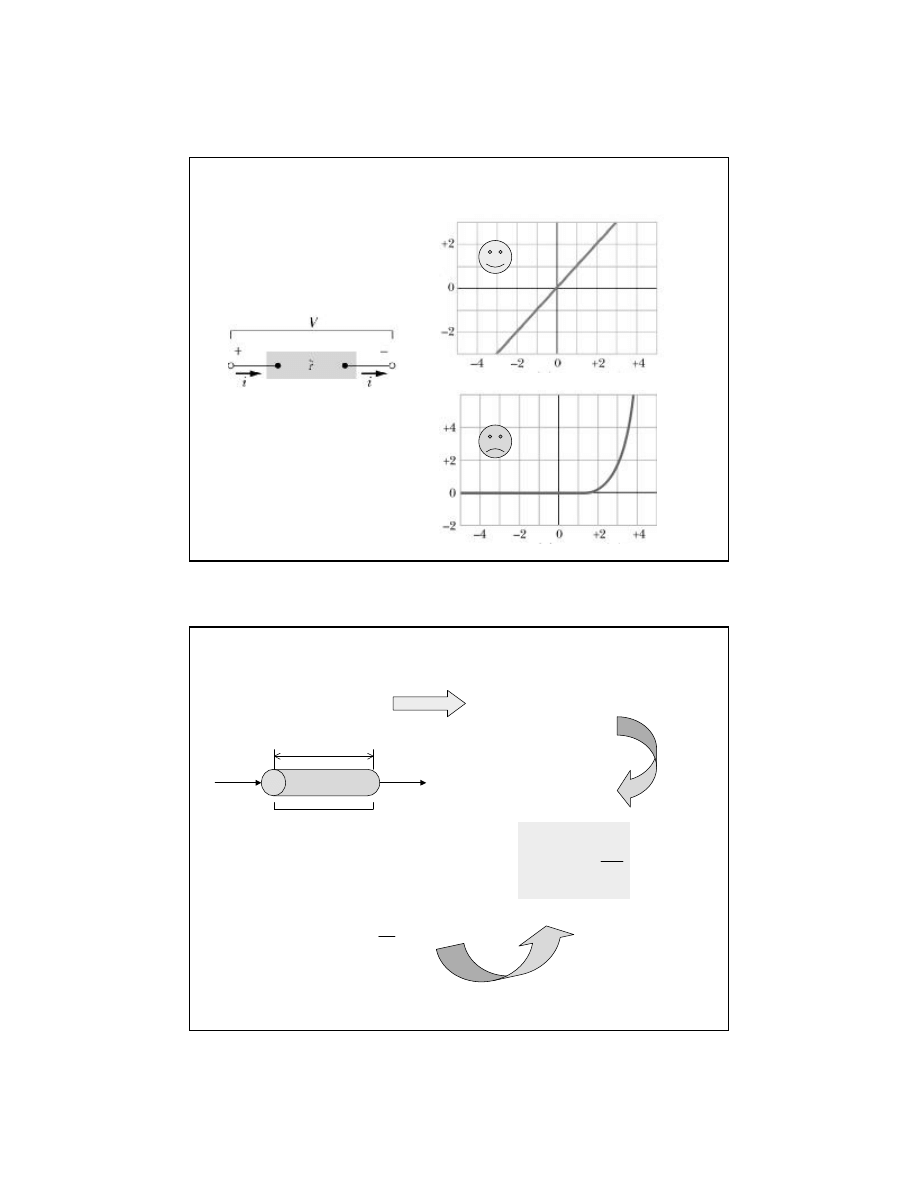
11

Czy jest spe

łnione prawo Ohma

?

I(mA)

I(mA)

U(V)

U(V)

Od postaci mikroskopowej do makroskopowej

j

E

r

r

ρ

=

I

R

U

=

EL

V

U

=

∆

=

L

S

I

ρ

jL

ρ

U

=

=

S

L

ρ

R

=

S

L

U

I

I

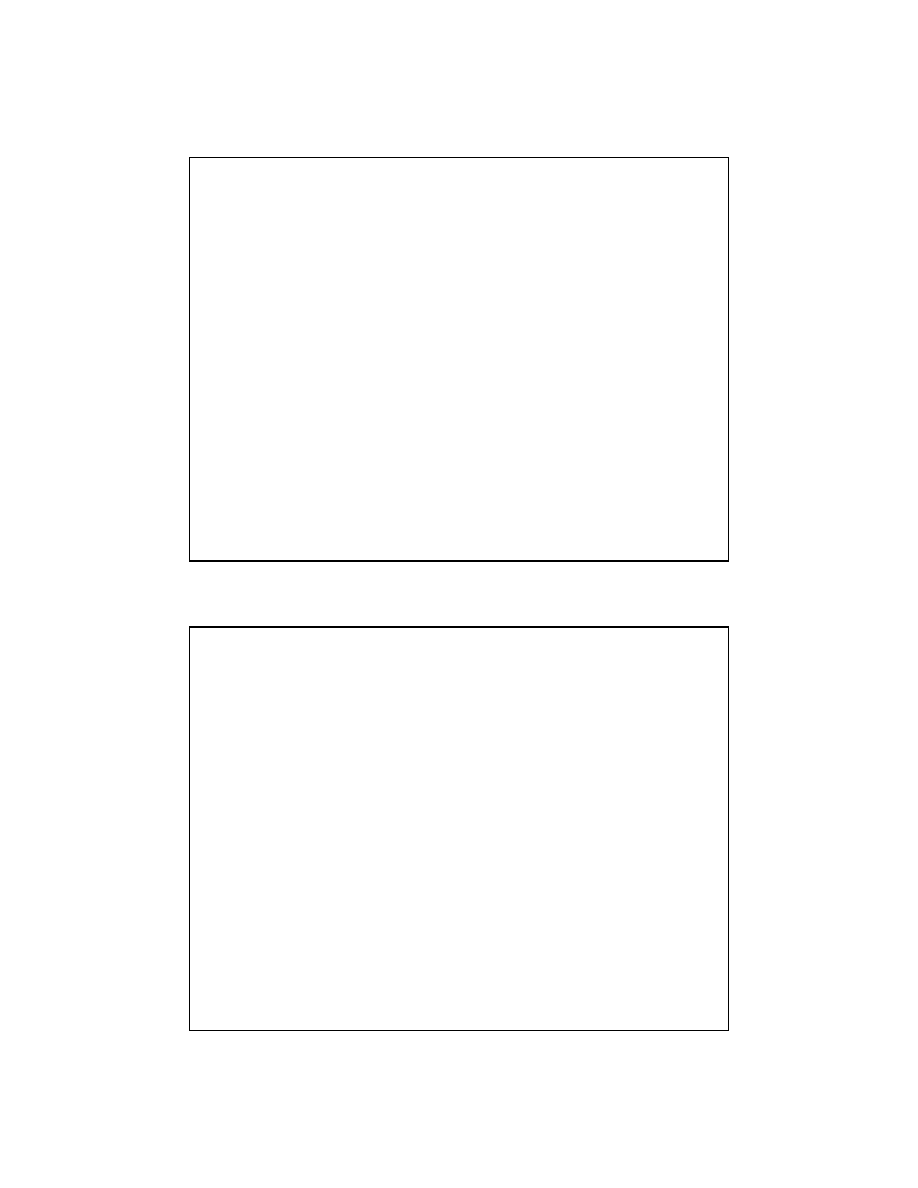
12

Zadanie domowe-3

(a) Ile wynosi

średni czas między zderzeniami dla

elektronów przewodnictwa miedzi?

(b)

Średnia droga swobodna λ elektronów przewodnictwa

jest

średnią odległością, przebywaną przez elektron

mi

ędzy zderzeniami. Jaka jest wartość λ dla miedzi?

Przyj

ąć wartość prędkości efektywnej v

eff

=1,6·10

6

m/s.

τ

Zadanie domowe-4

W przewodniku chromonikielinowym (czyli ze stopu Ni-Cr-
Fe, u

żywanego powszechnie w elementach grzejnych) o

d

ługości 1 m i przekroju poprzecznym 1 mm

2

p

łynie prąd o

nat

ężeniu 4 A przy różnicy potencjałów 2 V, przyłożonej do

jego ko

ńców. Obliczyć konduktywność chromonikieliny.

Zadanie domowe-5

Przeczyta

ć rozdziały 27.8 oraz 27.9 podręcznika HRW, tom 3.

Na tej podstawie przygotuj si

ę do odpowiedzi na pytania

dotycz

ące:

• Pó

łprzewodników (semiconductors)

• Nadprzewodników (superconductors)

Co rozumiesz pod poj

ęciem nadprzewodniki

wysokotemperaturowe? Czy wiesz,

że z tym odkryciem wiąże

si

ę nagroda Nobla? Poszukaj kto i kiedy ją zdobył.

13

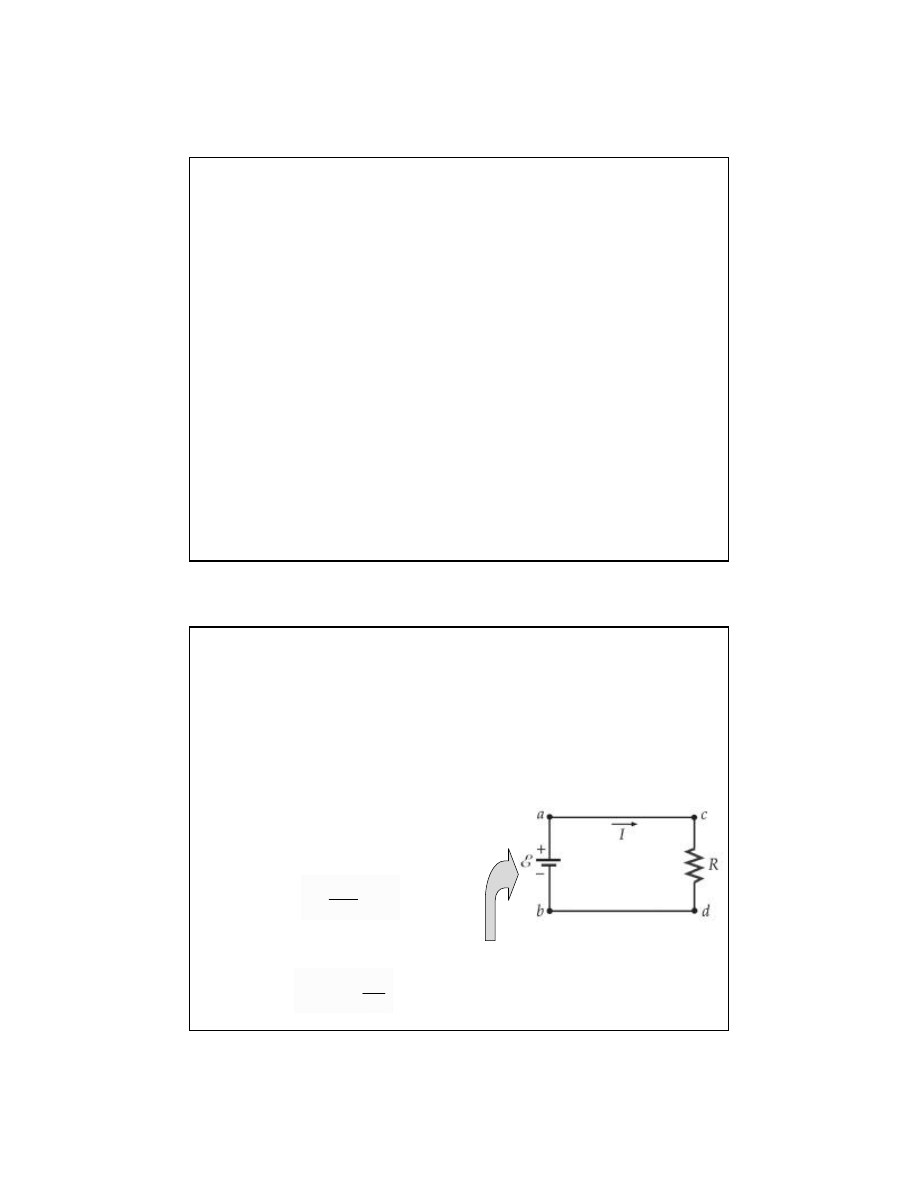
OBWODY ELEKTRYCZNE

Energia i moc w obwodzie

elektrycznym

źródło prądu lub
napi

ęcia, siła

elektromotoryczna

Energia potencjalna tracona w obwodzie:

U

Idt

U

dq

dE

p

=

=

Rdt

I

dQ

2

=

Moc zwi

ązania z przekazem energii

UI

dt

dE

P

p

=

=

a gdy spe

łnione jest prawo Ohma

R

U

R

I

P

2

2

=

=

zamienia si

ę w inny rodzaj energii (np. na elemencie rezystancyjnym na

ciep

ło Joule’a)

14

Si

ła elektromotoryczna SEM

• Aby wytworzy

ć stały przepływ ładunku, potrzebne

jest urz

ądzenie, które wykonywałoby pracę nad

no

śnikami ładunku, utrzymując stałą różnicę

potencja

łów

• Urz

ądzenie takie nazywamy źródłem siły

elektromotorycznej (

źródłem SEM)

• Si

ła elektromotoryczna nie jest siłą!!!

• Stosowane

źródła SEM to: ogniwa elektryczne

(baterie), pr

ądnice elektryczne, ogniwa

s

łoneczne, ogniwa paliwowe, termoogniwa

Zadanie domowe-6

Przygotowa

ć materiały dotyczące różnych rodzajów ogniw:

w tym tradycyjnych i niekonwencjonalnych (s

łonecznych,

paliwowych, etc.) Zagadnienie to mie

ści się w bardziej

ogólnym temacie: Fotowoltaika i niekonwencjonalne

źródła

energii, który jest obecnie szczególnie rozwijany w
o

środkach naukowych w Polsce i na świecie.

15

Definicja SEM: si

ła elektromotoryczna źródła SEM jest pracą,

przypadaj

ącą na jednostkę ładunku, jaką wykonuje źródło,

przenosz

ąc ładunek z bieguna na mniejszym potencjale do

bieguna o wy

ższym potencjale

dq

dW

ε

=

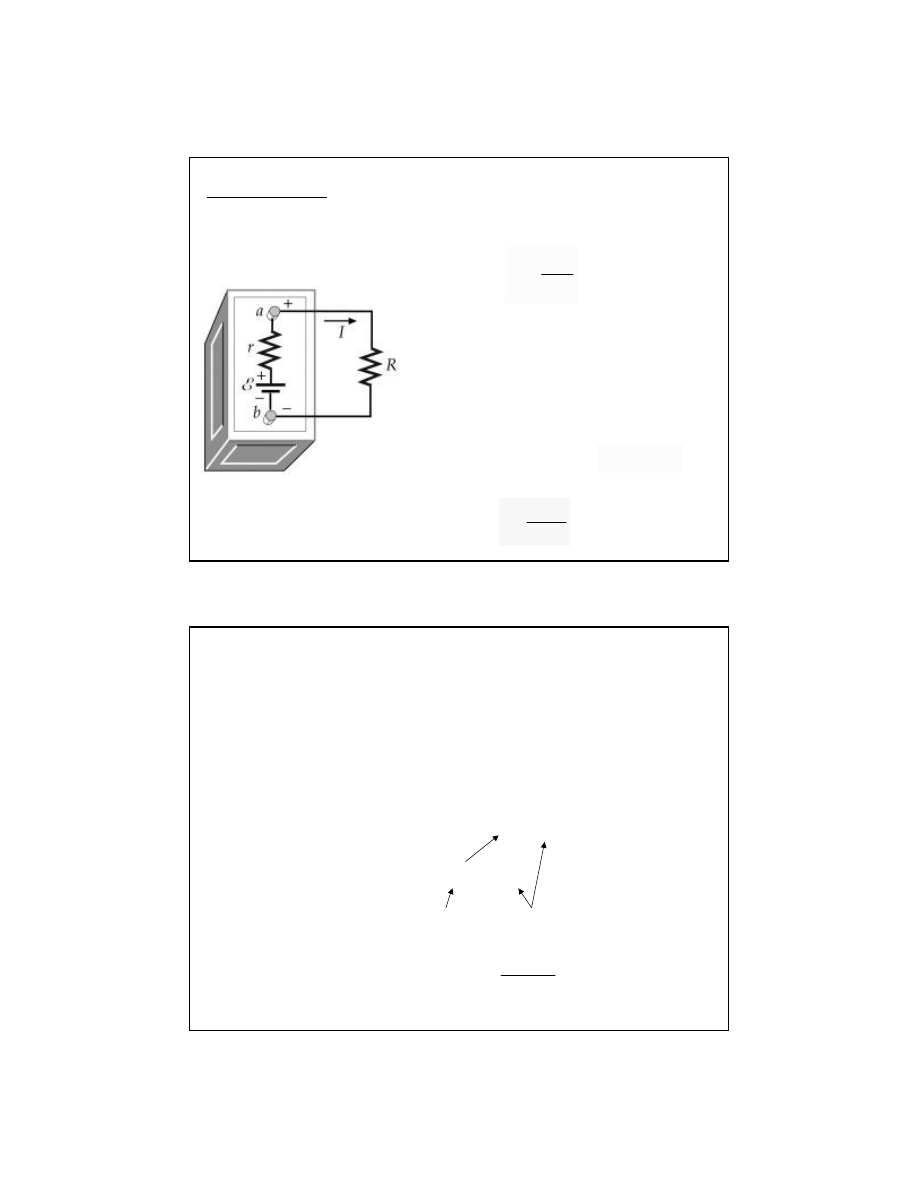
Rzeczywiste

źródło SEM zawiera

zawsze opór wewn

ętrzny r. Gdy

ogniwo jest otwarte, tj. pr

ąd nie

p

łynie, to różnica potencjałów

mi

ędzy biegunami ogniwa V

ab

=

ε

Gdy pr

ąd płynie to:

ab

V

Ir

-

ε

=

IR

V

ab

=

r

R

I

+

ε

=

Ir

U

−

=

ε

R

r)

(R

ε

R

I

P

2

2

2

+

=

=

moc rozproszona w

źródle

Wypadkowa szybko

ść przekazywania energii ze źródła SEM (moc):

UI

P

w

=

ale:

r

I

εI

I

Ir)

(ε

P

2

w

−

=

−

=

czyli:

r

SEM

w

P

P

P

−

=

moc

źródła SEM

Z drugiej strony, moc
wydzielana na obci

ążeniu R

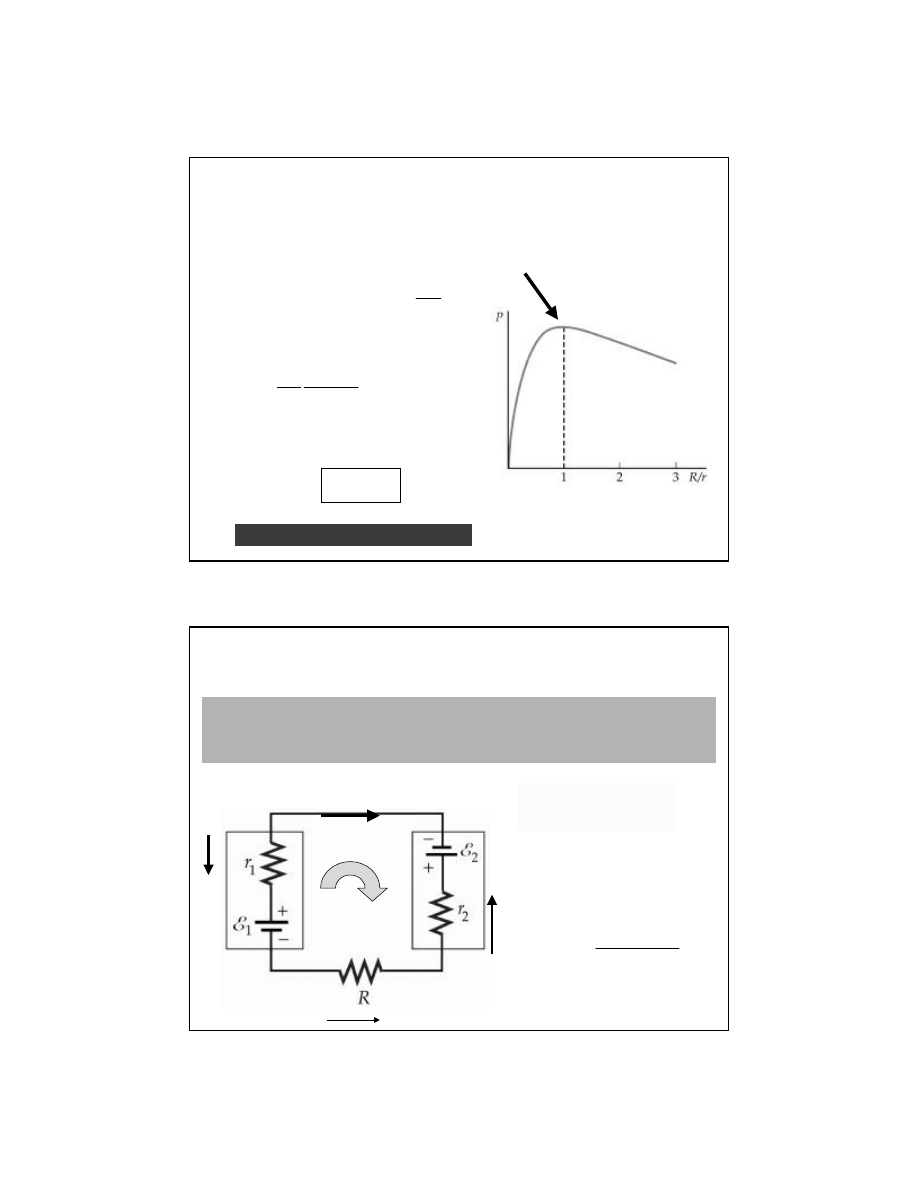
Moc i SEM

16

Dopasowanie mocy

0

dR

dP

=

Maksymalna moc wydzielana na obci

ążeniu wystąpi gdy:

warunek dopasowania mocy dla obci

ążenia R

r

R

=

0

R

r)

(R

ε

dR

d

2

2

=

+

tj., gdy

Ale

źródło zużywa się najszybciej!!

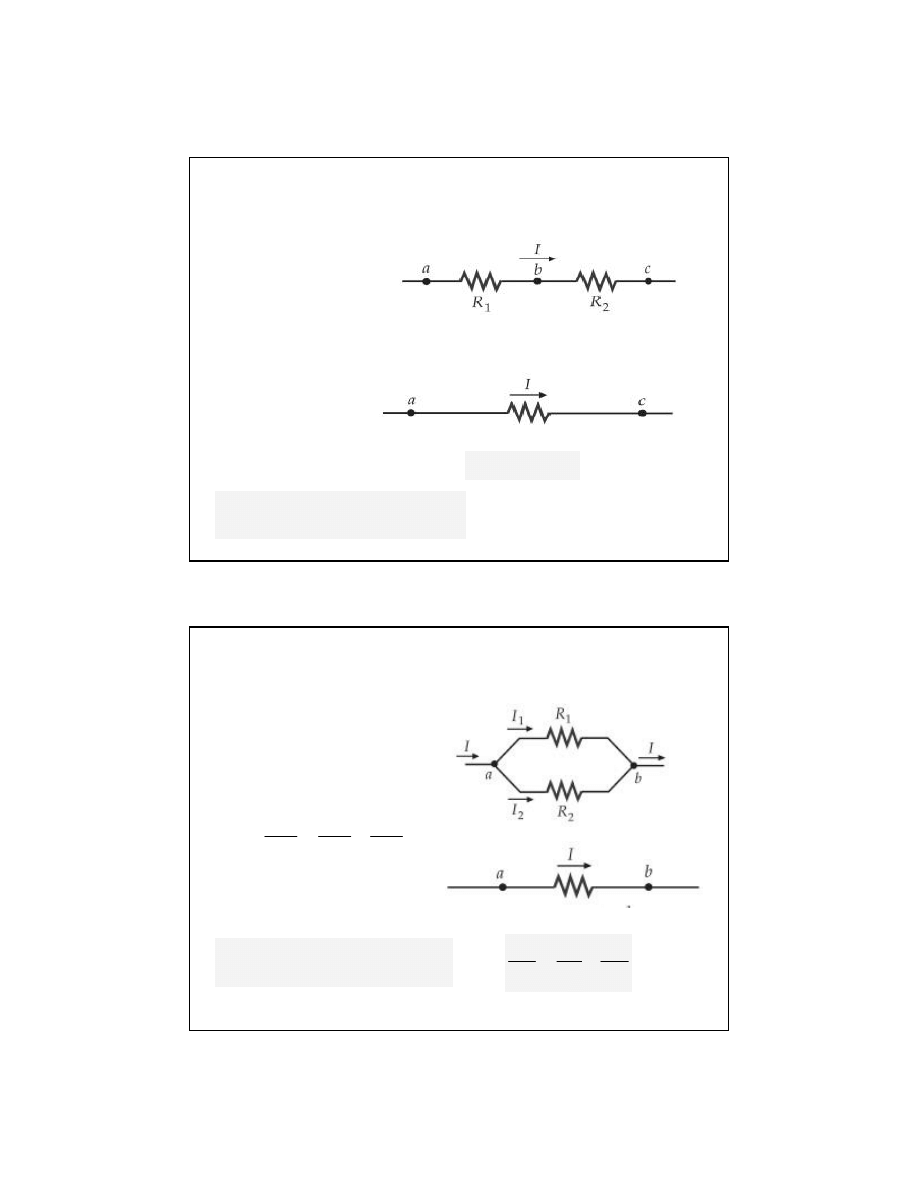
II Prawo Kirchhoffa

Algebraiczna suma zmian potencja

łów przy pełnym

obiegu dowolnego oczka musi by

ć równa zeru.

0

)

i

U

i

(ε

=

+

∑

+

Ir

1

Ir

2

IR

I

0

IR

Ir

ε

Ir

ε

2

2

1

1

=

−

−

+

−

2

1

2

1

r

r

R

I

+

+

ε

+

ε

=

17

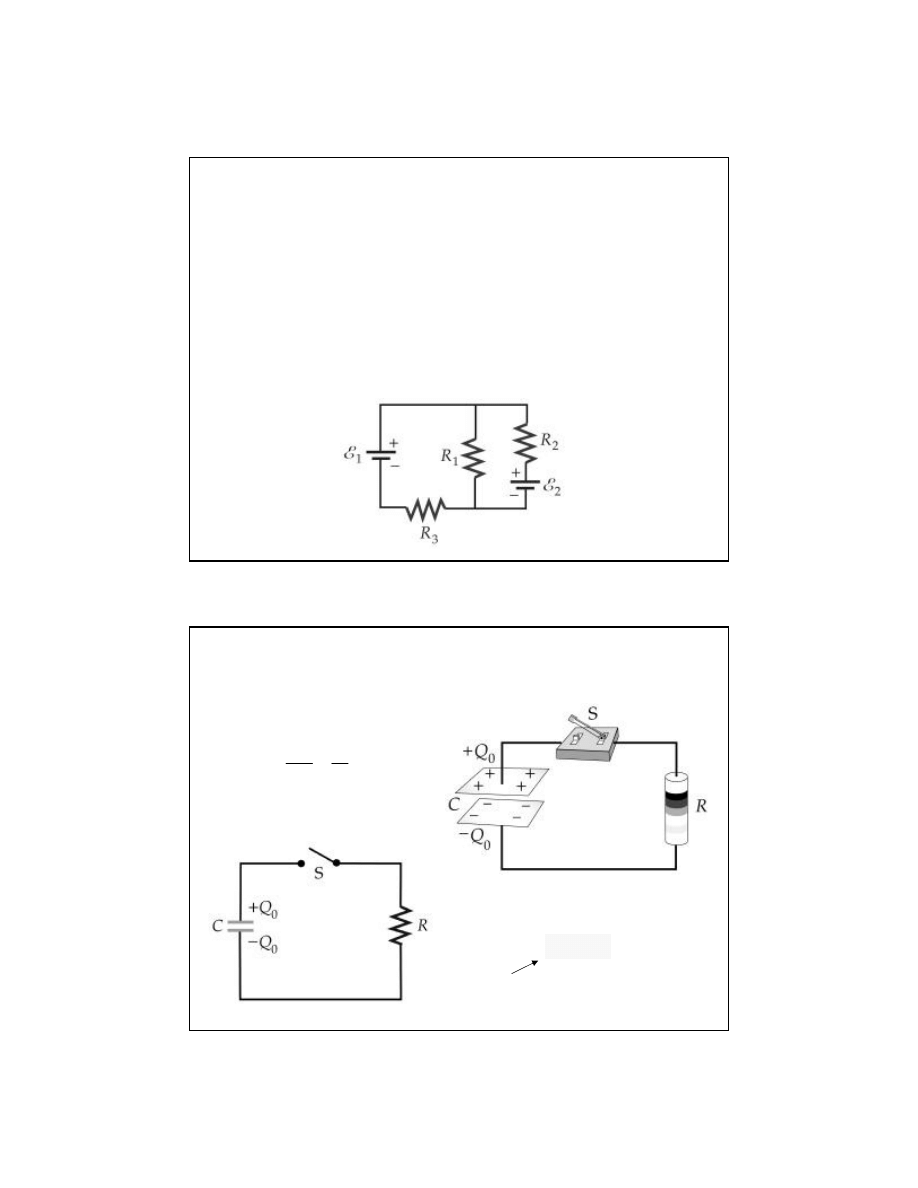
Po

łączenie szeregowe rezystancji

bc

ab

ac

V

V

V

+

=

)

R

R

(

I

IR

IR

V

2

1

2

1

ac

+

=

+

=

2

1

z

R

R

R

+

=

Rezystancja zast

ępcza

po

łączenia szeregowego

Po

łączenie równoległe rezystancji

Rezystancja zast

ępcza

po

łączenia równoległego

2

1

z

R

1

R

1

R

1

+

=

2

1

I

I

I

+

=

2

ab

1

ab

z

ab

R

V

R

V

R

V

+

=

18

Zadanie domowe-7

Zapisa

ć równania Kirchhoffa dla wszystkich oczek

w obwodzie. Wyznaczy

ć wartości natężeń prądu w

poszczególnych ga

łęziach obwodu oraz spadki

napi

ęć na poszczególnych rezystorach w obwodzie.

Za

łożyć, że:

ε

1

=11 V,

ε

2

=12 V, R

1

=R

2

=10

Ω, R

3

=1

Ω

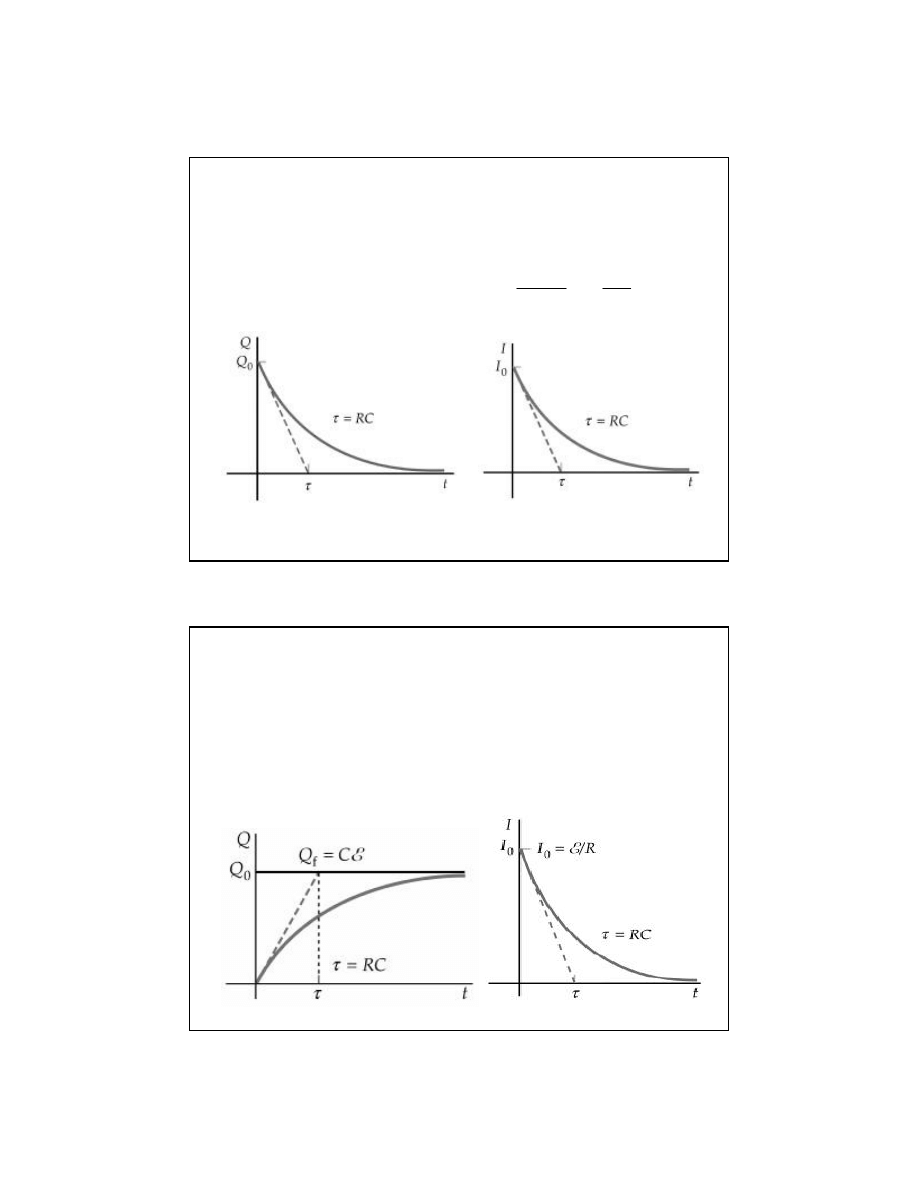
Obwody RC

Roz

ładowanie kondensatora

0

C

Q

dt

dQ

R

=

+

o

o

CU

Q

)

0

t

(

Q

=

=

=

/τ

t

o

e

Q

)

t

(

Q

−

=

RC

τ

=

sta

ła czasowa rozładowania kondensatora

19

Krzywe roz

ładowania kondensatora

/τ

t

o

e

Q

)

t

(

Q

−

=

/τ

t

o

e

τ

Q

dt

)

t

(

dQ

I

−

−

=

=

Zadanie domowe-8

Zapisz równanie obwodu dla

ładowania

kondensatora. Podaj rozwi

ązanie i sprawdź czy

odpowiada ono przedstawionym poni

żej wykresom

20

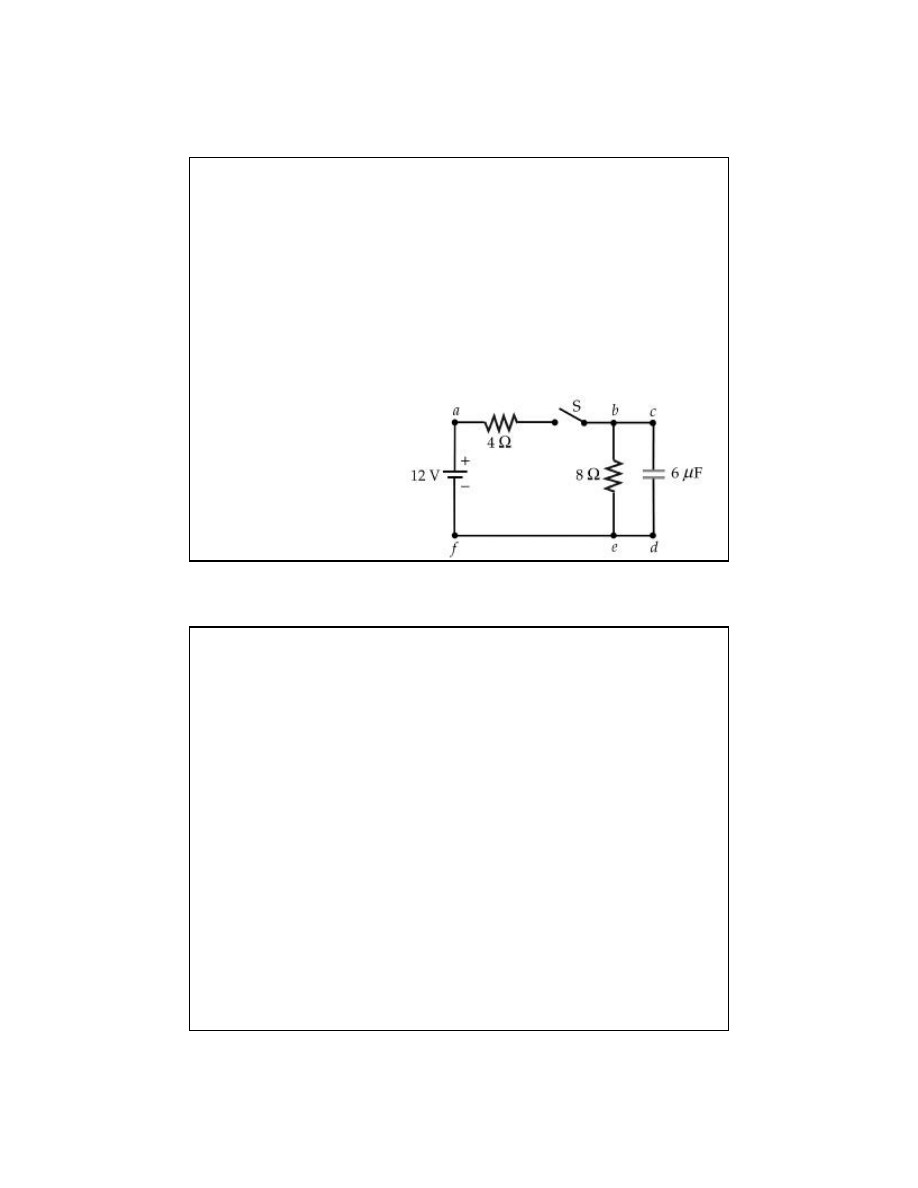
Zadanie domowe-9

Kondensator o pojemno

ści 6μF jest początkowo nie

na

ładowany. Znaleźć natężenie prądu płynącego przez

rezystor 4

Ω i rezystor 8 Ω:

(a) natychmiast po zamkni

ęciu klucza S,

(b) po bardzo d

ługim czasie od zamknięcia klucza S.

(c) Znale

źć ładunek na kondensatorze po bardzo długim

czasie od zamkni

ęcia klucza

Podsumowanie

• Pr

ąd elektryczny jest uporządkowanym ruchem

no

śników ładunku, wywołanym polem elektrycznym w

przewodniku pod wp

ływem różnicy potencjałów.

• No

śnikami ładunku są elektrony w metalach ale

elektrony i dziury w pó

łprzewodnikach. W przewodnikach

jonowych (NaCl) mog

ą to być dodatnie i ujemne jony.

• Rozpraszanie no

śników ładunku na defektach sieci, np.

drgaj

ących wokół położeń równowagi jonach, powoduje

pojawienie si

ę oporu elektrycznego (rezystancja,

rezystywno

ść) zależnego od temperatury.

• Prawo Ohma podaje zale

żność liniową pomiędzy polem

elektrycznym i g

ęstością prądu (mikroskopowo) lub

napi

ęciem i natężeniem (makroskopowo). Prawo to nie

zawsze jest spe

łnione.

• Do rozwi

ązywania obwodów elektrycznych konieczna

jest znajomo

ść praw Kirchhoffa.