
Elementy
analizy
matematycznej
Granice funkcji
Funkcja f ma w punkcie x
o
granic
ę
G
, gdy dla dowolnego ci
ą
gu (x
n
) o
wyrazach nale
żą
cych do s
ą
siedztwa S(x
o
) i zbie
ż
nego do x
o
,
odpowiadaj
ą
cy mu ci
ą
g warto
ś
ci funkcji (f(x
n
)) ma granic
ę
równ
ą
G,
co mo
ż
emy zapisa
ć
:
)]
)
(
lim
(
)
lim
,
),
(
[(
)
(
lim
(
)
(
G
x
f
x
x
N
n
x
S
x
G
x
f
n
n
o
n
n
o
n
x
def
x
x
n
o
=
⇒
=
∈
∈
∧
⇔
=
∞
→
∞
→
→
Gdy granica jest sko
ń
czona (G) to nazywamy j
ą
wła
ś
ciw
ą
W przypadku zast
ą
pienia symbolu G
±∞
to granic
ę
nazywamy
niewła
ś
ciw
ą
Definicja Heinego:
Istnienie granicy funkcji mówi nam o zachowaniu funkcji w s
ą
siedztwie
danego punktu, nie daje
ż
adnej informacji o warto
ś
ci funkcji w tym punkcie.
Funkcja nie musi by
ć
okre
ś
lona w punkcie, którym istnieje granica
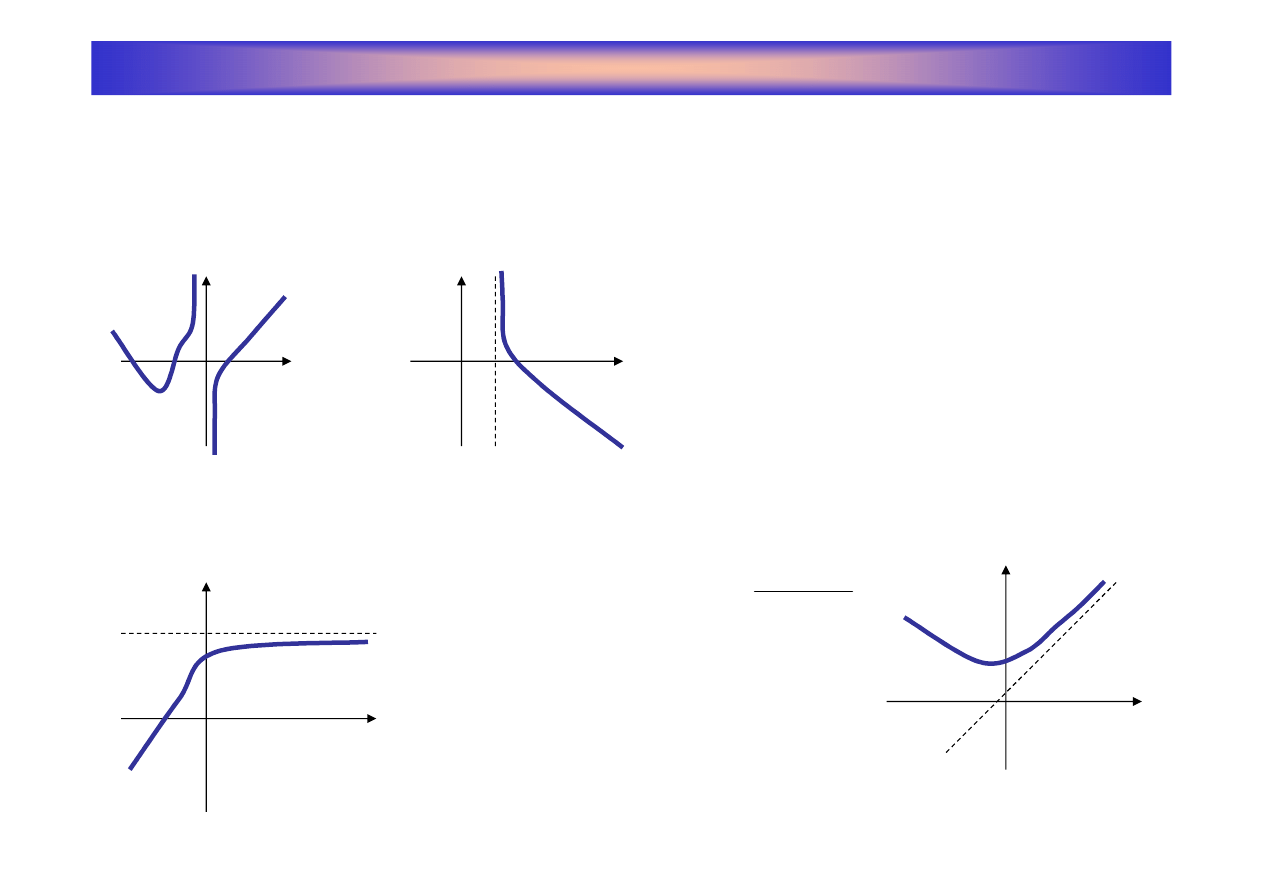
Asymptot
ą
pionow
ą
jest prosta o równaniu x=a gdy:
±∞
=
−
→
)
(
lim
x
f
a
x
±∞
=
+
→
)
(
lim
x
f
a
x
lub
obustronna jednostronna
Asymptot
ą
poziom
ą
jest prosta o równaniu
y=a gdy:
a
x
f
x
=
±∞
→
)
(
lim
Asymptot
ą
uko
ś
n
ą
jest prosta o
równaniu y=ax+b gdy istniej
ą
wła
ś
ciwe granice:
x
x
f
a
x
)
(
lim
±∞
→
=
]
)
(
[
lim
ax
x
f
b
x
−
=
±∞
→
Asymptoty
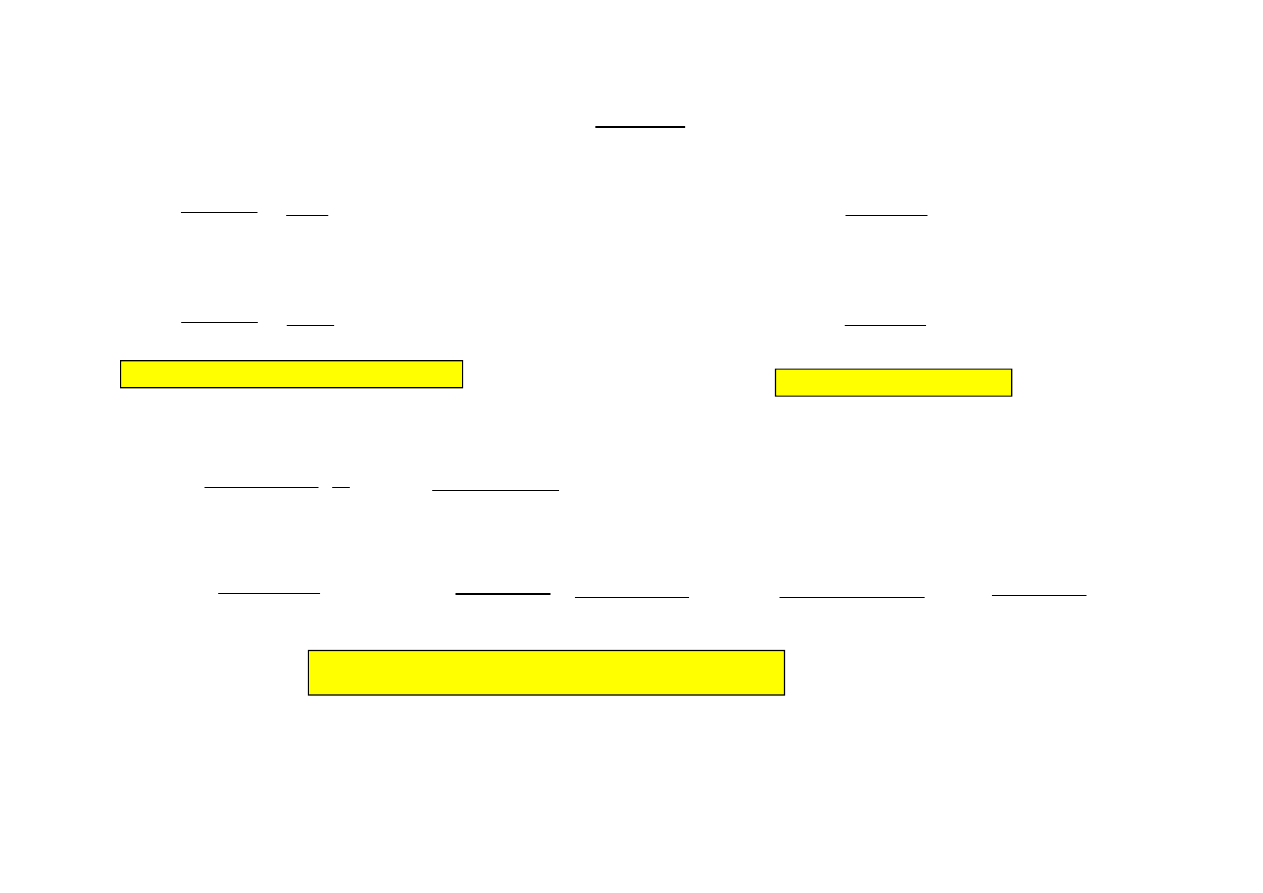
Wyznaczy
ć
asymptoty krzywej:
2
3
)
1
(
)
(
x
x
x
f
−
=
1
≠
x
=
−
−
→
2
3
1
)
1
(
lim
x
x
x
=
−
+
→
2
3
1
)
1
(
lim
x
x
x
]
0
[
]
1
[
+
+∞
=
]
0
[
]
1
[
+
+∞
=
1
=
x
obustronna
pionowa
asymptota
=
−
−∞
→
2
3
)
1
(
lim
x
x
x
=
−
∞
→
2
3
)
1
(
lim
x
x
x
∞
−
∞
+
poziomej
asymptoty
brak
=
⋅
+
−
=
∞
→
x
x
x
x
a
x
1
2
1
lim
2
3
=
+
−
∞
→
3
2
3
2
lim
x
x
x
x
x
1
∞
→
=
x
b
lim
=
−
+
−
)
2
1
(
2
3
x
x
x
x
∞
→
x
lim
−
+
−
2
3
2
1
(
x
x
x
=
+
−
+
−
)
2
1
)
2
1
(
2
2
x
x
x
x
x
∞
→
x
lim
=
+
−
−
+
−
2
3
2
3
2
1
2
x
x
x
x
x
x
∞
→
x
lim
=
+
−
+
−
2
2
2
1
2
x
x
x
x
2
istnieje asymptota uko
ś
na y=x+2
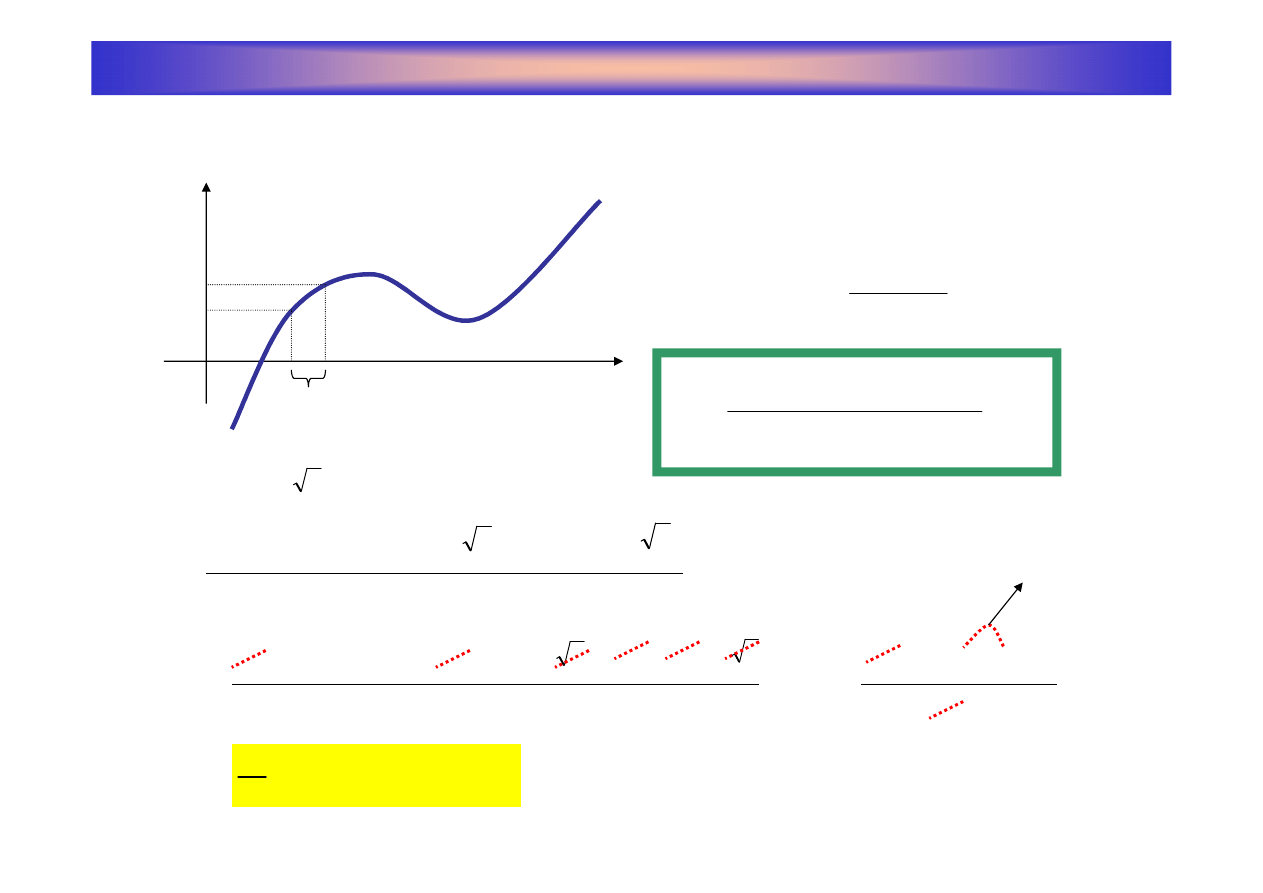
Pochodna funkcji w punkcie
f(x)
x
o
x
1
y
o
y
1
Iloraz ró
ż
nicowy
o
o
x
x
y
y
−
−
1
1
dx
dx
x
f
dx
x
f
o
o
)
(
)
(
−
+
0
lim
→
dx
2
8
4
)
(
2
−
+
=
x
x
x
f
0
lim
→
dx
]
2
)
(
8
)
(
4
[
2
−
+
+
+
dx
x
dx
x
o
o
]
2
8
4
[
2
−
+
−
o
o
x
x
dx
=
=
0
lim
→
dx
dx
2
8
8
)
(
4
8
4
2
2
−
+
+
+
+
dx
x
dx
dx
x
x
o
o
o
2
8
4
2
+
−
−
o
o
x
x
=
0
lim
→
dx
)
8
4
8
(
+
+
dx
x
dx
o
dx
8
8
+
=
o
x
8
8
)
(
'
+
=
=
x
x
f
dx
df
0
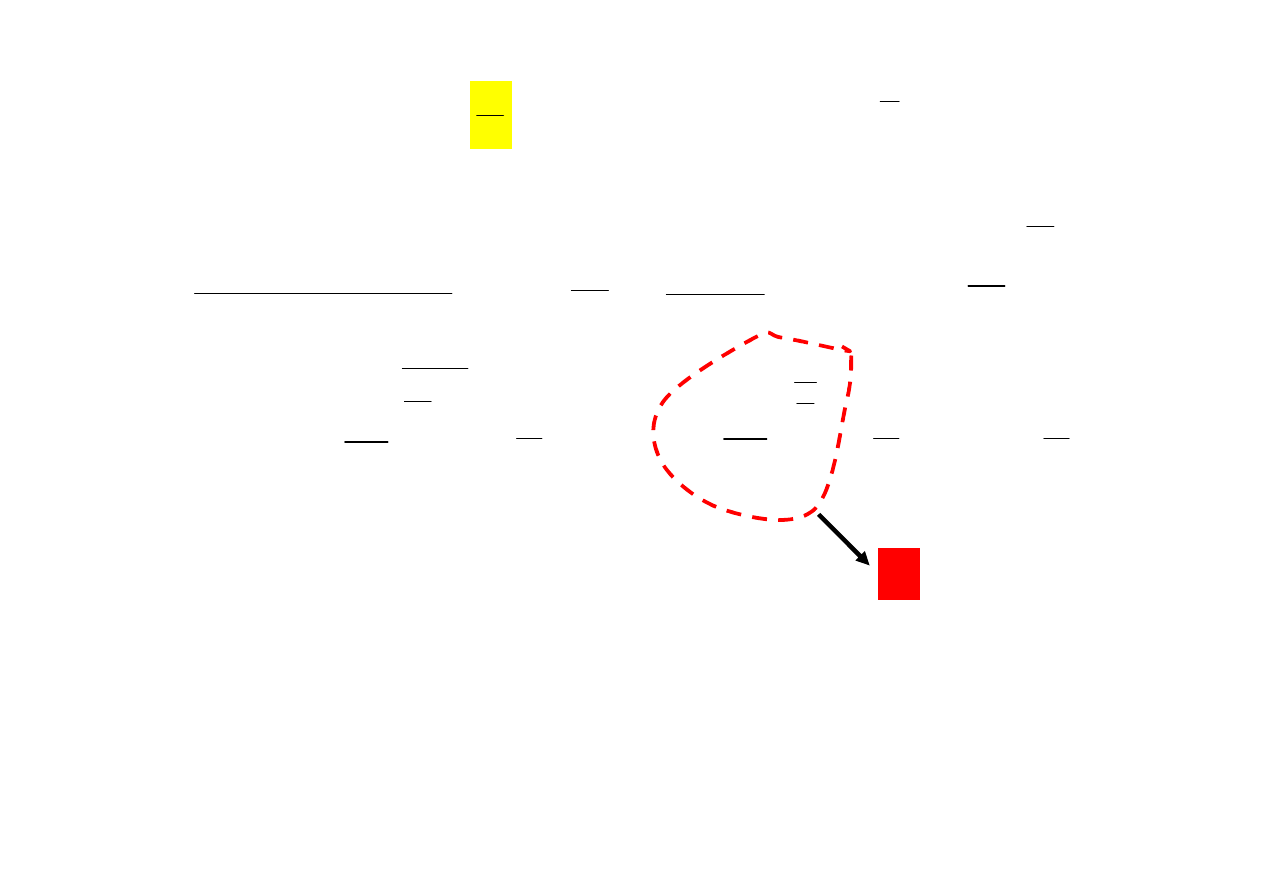
e
m
m
m
=
+
→
1
0
)
1
(
lim
?
)
(
'
ln
)
(
=
=
x
f
x
x
f
0
lim
→
dx
dx
x
dx
x
o
o
)
ln(
)
ln(
−
+
=
⋅
dx
1
0
lim
→
dx
+
o
o
x
dx
x
ln
0
lim
→
dx
=
dx
1
+
o
x
dx
1
ln
=
=
e
0
lim
→
dx
+
0
1
ln
x
dx
0
0
1
x
x
dx
⋅
=
o
x
1
0
lim
→
dx
+
0
1
ln
x
dx
0
1
x
dx
=
e
ln
o
x
1
=
o
x
1
x
1

Podstawowe wzory i twierdzenia rachunku ró
ż
niczkowego
0
)'
(
=
C
0
,
,
)'
(
1
>
∈
=
−
x
R
x
x
α
α
α
α
x
x
cos
)'
(sin
=
x
x
sin
)'
(cos
−
=
a
a
a
x
x
ln
)'
(
=
x
x
e
e
=
⇒
)'
(
a
x
x
a
ln
1
)'
(log
=
x
x
1
)'
(ln
=
⇒
)
(
'
)
(
'
)]'
(
)
(
[
x
g
x
f
x
g
x
f
±
=
±
)
(
'
)]'
(
[
x
Cf
x
Cf
=
)
(
'
)
(
)
(
)
(
'
)]'
(
)
(
[
x
g
x
f
x
g
x
f
x
g
x
f
⋅
+
⋅
=
⋅
0
)
(
;
)]
(
[
)
(
'
)
(
)
(
)
(
'
'
)
(
)
(
2
≠
⋅
−
⋅
=
x
g
x
g
x
g
x
f
x
g
x
f
x
g
x
f
Przykłady:
=
)'
(tgx
=
−
x
x
x
x
x
2
cos
)'
(cos
sin
cos
)'
(sin
=
'
cos
sin
x
x
=
−
−
x
x
x
x
x
2
cos
)
sin
(
sin
cos
cos
=
+
x
x
x
2
2
2
cos
sin
cos
x
2
cos
1
Jedynka
trygonometryczna
=
)'
(ctgx
x
2
sin
1
−
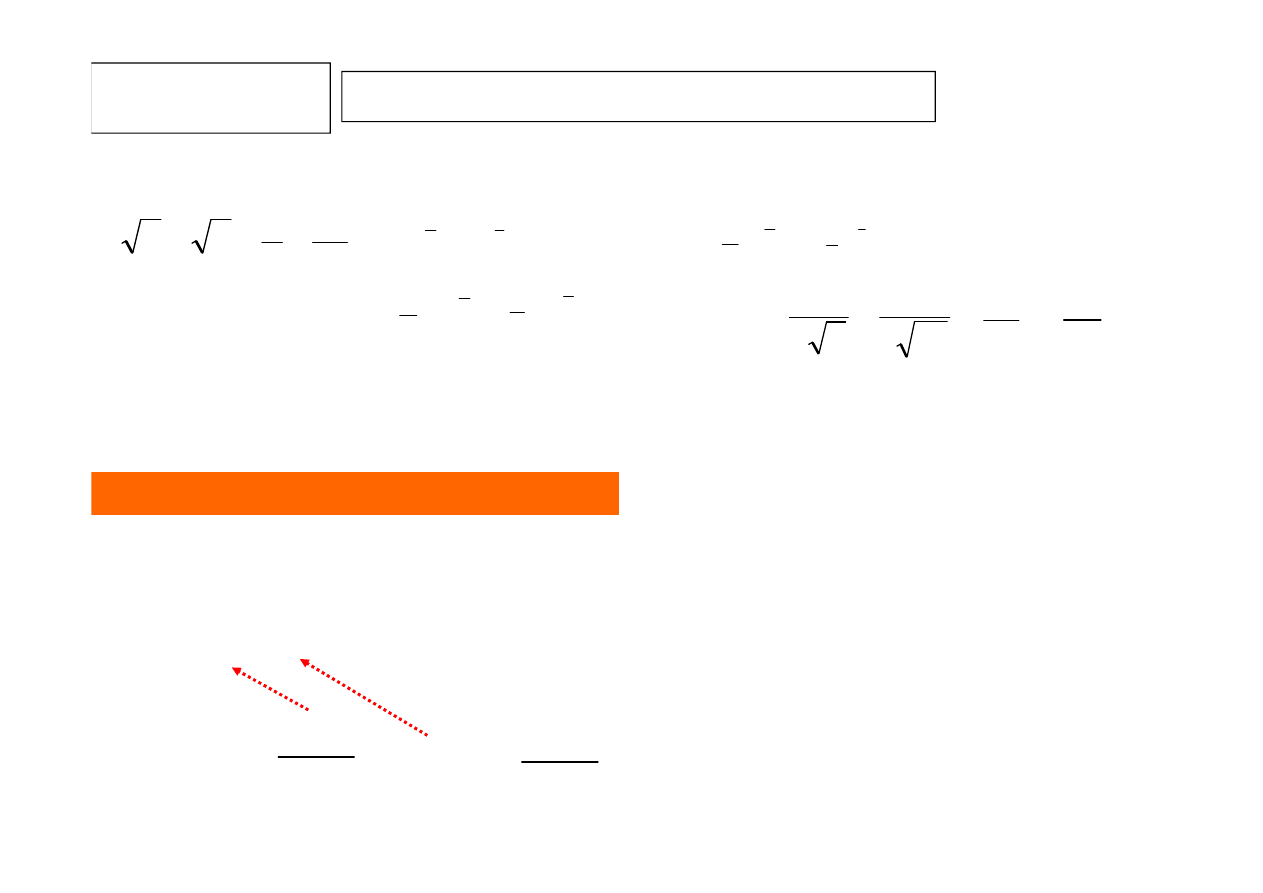
1
8
3
2
−
+
x
x
=
+
−
+
)'
3
4
(
2
3
x
x
x
=
+
−
+
'
3
'
)'
(
4
)'
(
2
3
x
x
x
=
−
+
−
)'
2
1
(
2
3
x
x
x
x
3
4
x
+
2
1
x
−
3
2
3
1
x
−
x
2
1
=
+
−
3
4x
2
−
−
x
3
2
3
1
−
−
x
2
1
2
1
−
x
=
+
−
−
1
2
4 x
1
1
−
−
−
x
1
3
1
3
1
−
−
x
1
2
1
2
1
−
x
=
−
−
)'
2
2
x
1
−
+
x
3
1
x
−
2
1
(x
1
)'
(
−
=
α
α
α
x
x
=
=
)'
( x
e
x
=
+
'
)'
(
x
e
x
e
x
x
=
+
x
x
e
x
e
)
1
(
+
x
e
x
Twierdzenie o pochodnej funkcji zło
ż
onej:
Je
ż
eli F(x)=f(g(x)) i funkcja g ma pochodn
ą
w punkcie x, a funkcja f ma pochodn
ą
w punkcie u=g(x), to funkcja F ma pochodn
ą
w punkcie x , przy czym:
F’(x)=f’(g(x))g’(x)
Przykłady:
=
+
))'
1
2
(ln( x
⋅
+
1
2
1
x
=
+
)'
1
2
( x
1
2
2
+
x
)
(
'
)
(
)
(
)
(
'
)]'
(
)
(
[
x
g
x
f
x
g
x
f
x
g
x
f
⋅
+
⋅
=
⋅
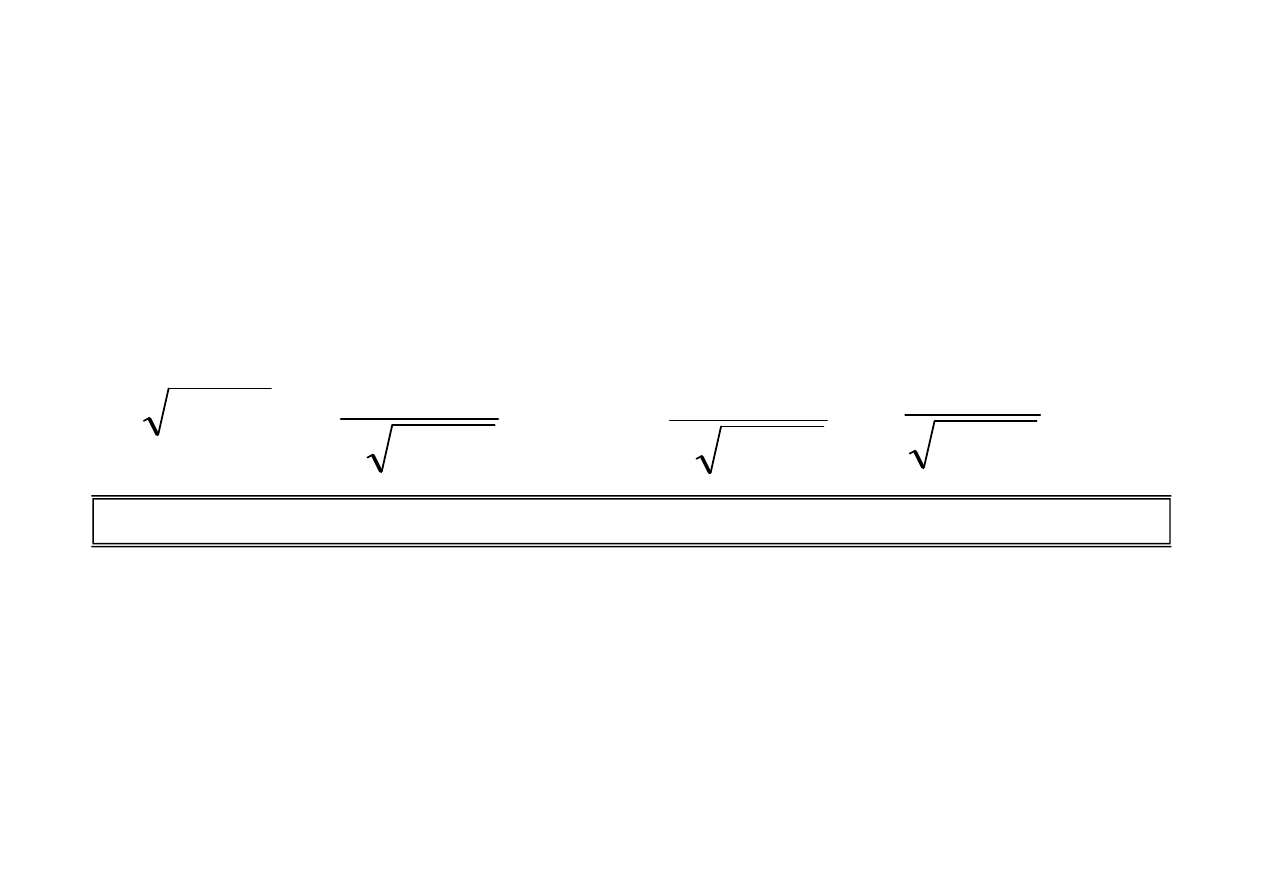
=
)'
(
sin x
e
)'
(sin
sin
x
e
x
x
e
x
cos
sin
=
=
−
]'
)
2
[(
100
3
x
=
−
−
)'
2
(
)
2
(
100
3
99
3
x
x
=
−
−
)
3
(
)
2
(
100
2
99
3
x
x
2
99
3
)
2
(
300
x
x
−
−
=
=
+
)'
3
(
2
x
=
+
+
)'
3
(
3
2
1
2
2
x
x
=
+
3
2
2
2
x
x
3
2
+
x
x
Pochodn
ą
drugiego rz
ę
du
nazywamy pochodn
ą
pierwszej pochodnej
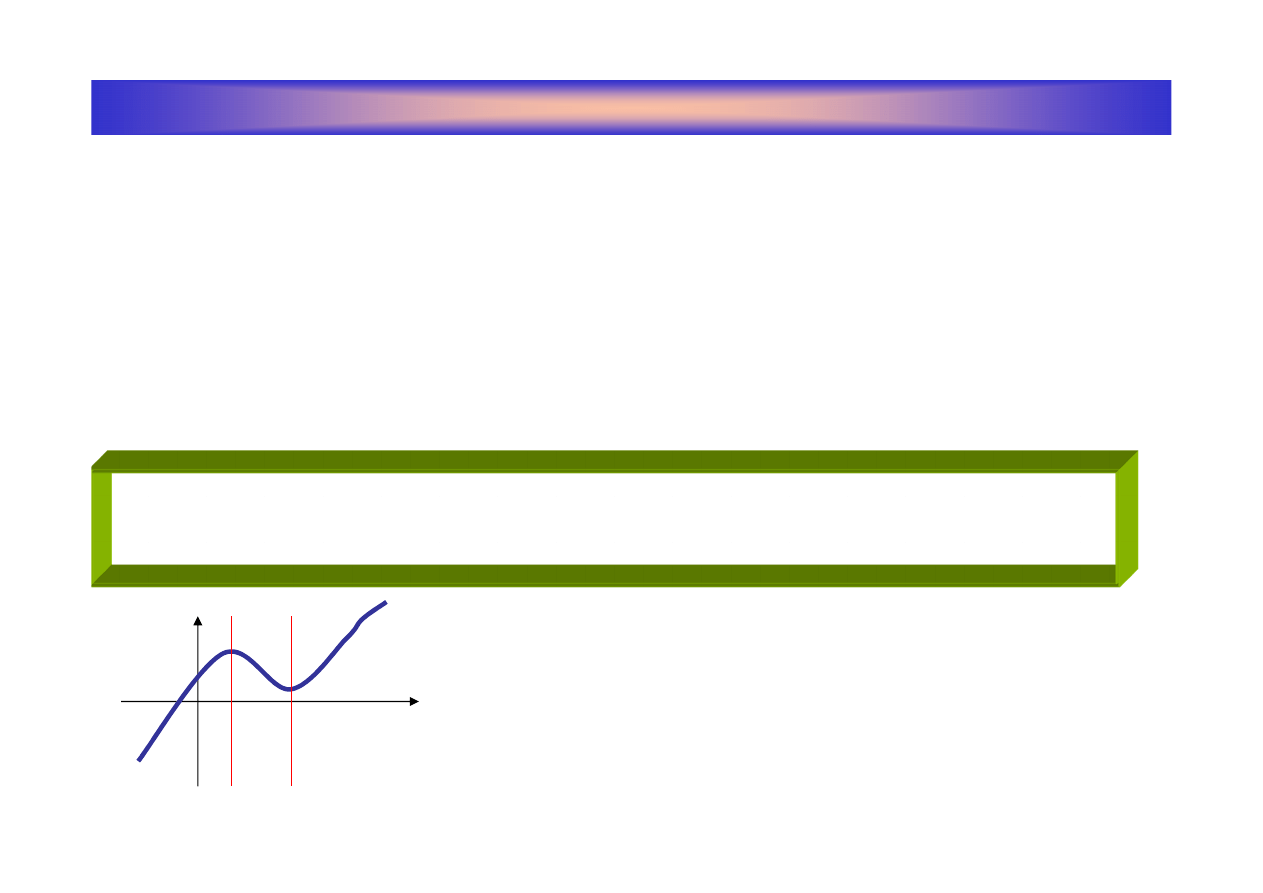
Przykład:
7
3
1
)
(
x
x
f
−
=
6
21
)
(
'
x
x
f
−
=
5
126
)
(
'
'
x
x
f
−
=
Ekstrema funkcji:
f’(x
o
)=0 - warunek konieczny istnienia ekstremum w punkcie x
o
,
ale niedostateczny
Pochodna przy przej
ś
ciu zmiennej x przez punkt x
o
zmienia znak z ujemnego
na dodatni (z dodatniego na ujemny), to funkcja y=f(x) osi
ą
ga ekstremum-
minimum (maksimum)
Je
ż
eli pierwsza pochodna funkcji jest
dodatnia
w pewnym przedziale, to funkcja
jest w tym przedziale
rosn
ą
ca
Je
ż
eli pierwsza pochodna funkcji jest
ujemna
w pewnym przedziale, to funkcja
jest w tym przedziale
malej
ą
ca
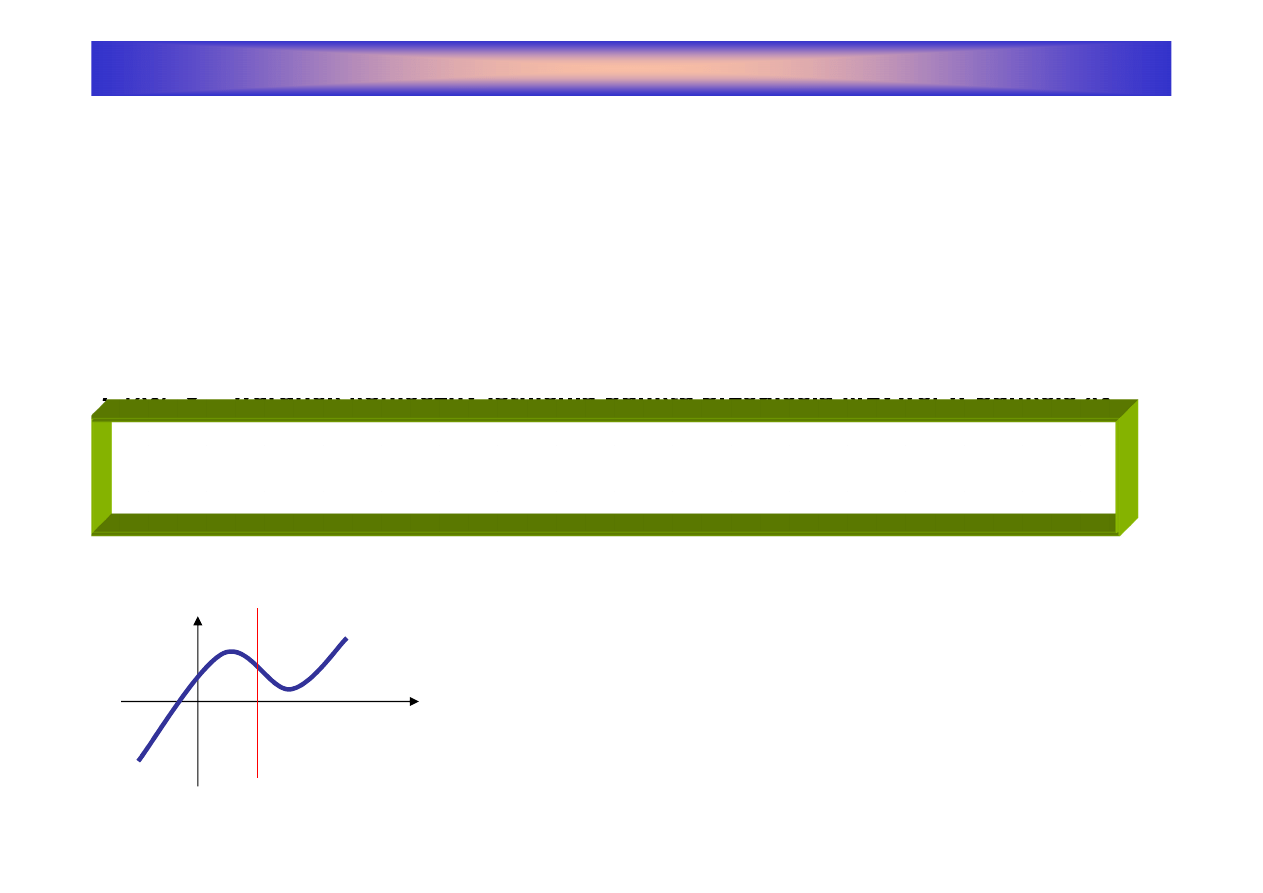
a
b
Pierwsza pochodna w przedziale :
(-
∞
;a)
ν
(b;
∞
) – jest dodatnia
(a;b) – jest ujemna
Dla x=a i x=b przyjmuje warto
ść
0
max
min
Punkty przegi
ę
cia:
f’’(x
o
)=0 - warunek konieczny istnienia punktu przegi
ę
cia krzywej w punkcie x
o
Druga pochodna przy przej
ś
ciu zmiennej x przez punkt x
o
zmienia znak z
ujemnego na dodatni (z dodatniego na ujemny), to funkcja y=f(x) osi
ą
ga
punkt
przegi
ę
cia
Je
ż
eli druga pochodna funkcji jest
dodatnia
w pewnym przedziale, to funkcja
jest w tym przedziale
wypukła
Je
ż
eli druga pochodna funkcji jest
ujemna
w pewnym przedziale, to funkcja jest
w tym przedziale
wkl
ę
sła
x
o
Druga pochodna w przedziale :
(-
∞
; x
o
)– jest ujemna
(x
o
;
∞
) – jest dodatnia
Dla x=x
o
przyjmuje warto
ść
0

Badanie przebiegu zmienno
ś
ci funkcji:
1) Dziedzina
2) Punkty przeci
ę
cia z osiami układu współrz
ę
dnych
3) Granice i wnioski dotycz
ą
ce istnienia asymptot
4) Wyznaczenie pierwszej pochodnej i badanie jej znaku
5) Wyznaczenie drugiej pochodnej i badanie jej znaku
6) Budowa tabeli przebiegu zmienno
ś
ci funkcji
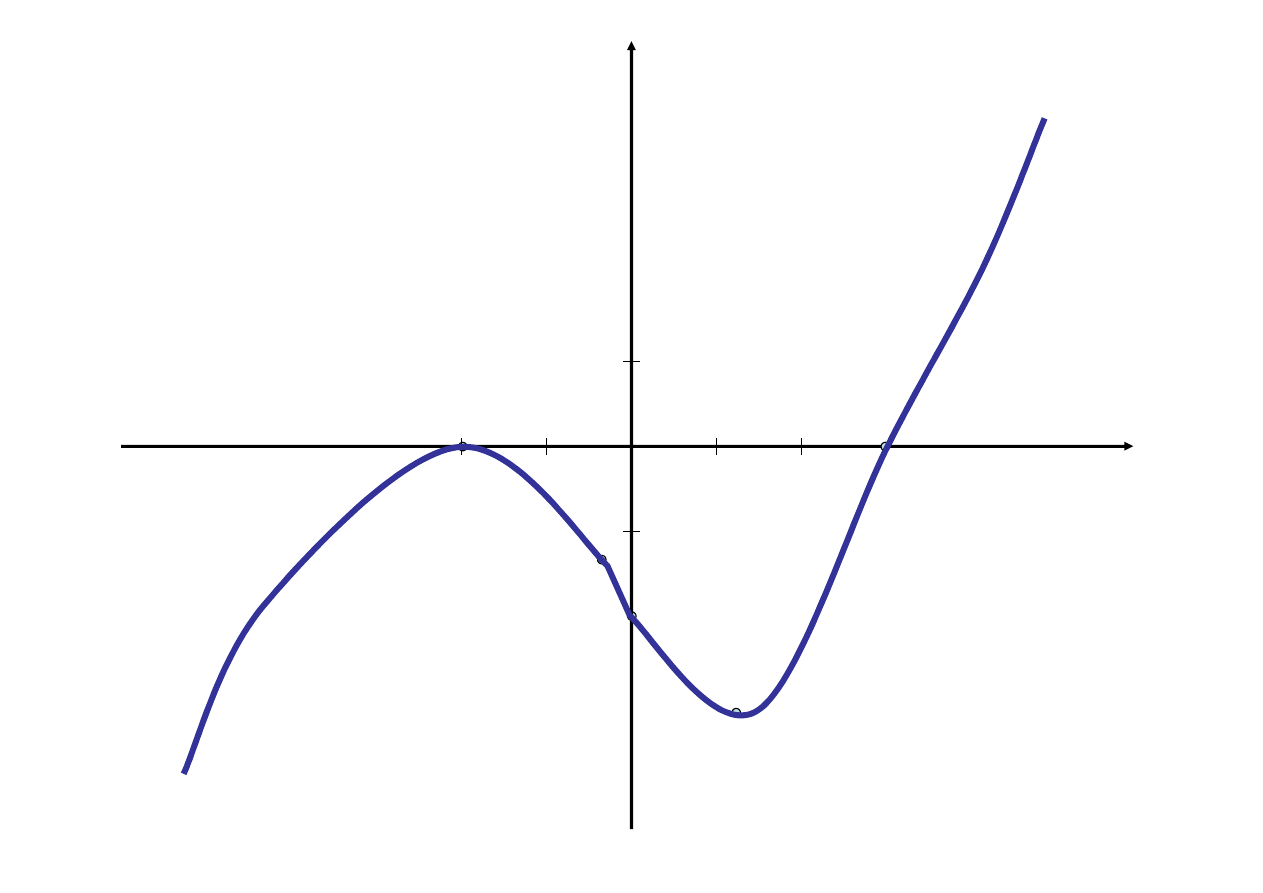
7) Szkic wykresu

Zbada
ć
przebieg zmienno
ś
ci funkcji:
)
3
(
)
2
(
)
(
2
−
+
=
x
x
x
f
1) Dziedzina
R
x
∈
2) Punkty przeci
ę
cia z osiami układu współrz
ę
dnych
12
)
0
(
−
=
f
Z postaci iloczynowej odczytujemy,
ż
e funkcja posiada miejsca zerowe dla x=-2 i x=3
12
4
12
4
3
)
3
)(
4
4
(
)
(
2
2
3
2
−
+
−
+
−
=
−
+
+
=
x
x
x
x
x
x
x
x
x
f
12
8
)
(
2
3
−
−
+
=
x
x
x
x
f
3) Granice i wnioski dotycz
ą
ce istnienia asymptot
−∞
→
x
lim
)
12
8
(
2
3
−
−
+
x
x
x
−∞
=
∞
→
x
lim
)
12
8
(
2
3
−
−
+
x
x
x
+∞
=
Funkcja nie posiada asymptot
4) Wyznaczenie pierwszej pochodnej i badanie jej znaku
=
−
−
+
=
)'
12
8
(
)
(
'
2
3
x
x
x
x
f
8
2
3
2
−
+
x
x
0
8
2
3
2
>
−
+
x
x
10
100
=
∆
⇒
=
∆
3
4
6
10
2
2
6
10
2
2
1
=
+
−
=
−
=
−
−
=
x
x
-2
4/3
)
;
(
)
2
;
(
3
4
+∞
∪
−
−∞
∈
x
Pochodna przyjmuje warto
ś
ci dodatnie w przedziale:
5) Wyznaczenie drugiej pochodnej i badanie jej znaku
=
−
+
=
)'
8
2
3
(
)
(
''
2
x
x
x
f
2
6
+
x
0
2
6
>
+
x
3
1
−
>
x
Pochodna przyjmuje warto
ś
ci dodatnie w przedziale:
)
;
(
3
1
∞
−
∈
x
6) Budowa tabeli przebiegu zmienno
ś
ci funkcji
f’(x)
f”(x)
f(x)
-
∞
26
,
9
12
)
(
8
)
(
)
(
)
(
3
1
2
3
1
3
3
1
3
1
−
=
−
−
−
−
+
−
=
−
f
52
,
18
12
8
)
(
)
(
)
(
3
4
2
3
4
3
3
4
3
4
−
=
−
⋅
−
+
=
f
∞
-
∞
…
…
∞
-2
…..
…..
…..
…..
-1/3
0
4/3
3
0
0
0
+
+
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
-
-9,26
-12
-18,52
0
0
Punkt
przegi
ę
cia
Minimum
Maksimum
-1
-6
6
2
3
4
)
(
2
−
−
+
=
x
x
x
x
f
2
≠
x
2
3
)
0
(
=
f
−
→
2
lim
x
+
→
2
lim
x
2
3
4
2
−
−
+
x
x
x
2
3
4
2
−
−
+
x
x
x
=
=
]
0
[
]
9
[
+
]
0
[
]
9
[
−
=
=
∞
−
∞
+
Asymptota pionowa obustronna x=2
−∞
→
x
lim
2
3
4
2
−
−
+
x
x
x
2
3
4
2
−
−
+
x
x
x
+∞
→
x
lim
∞
−
=
= ∞
+
Brak asymptoty poziomej
∞
→
x
lim
=
a
=
⋅
−
−
+
x
x
x
x
1
2
3
4
2
x
x
x
x
2
3
4
2
2
−
−
+
∞
→
x
lim
1
=
=
b
∞
→
x
lim
−
−
−
+
x
x
x
x
2
3
4
2
∞
→
x
lim
=
=
−
−
−
−
−
+
2
)
2
(
2
3
4
2
x
x
x
x
x
x
∞
→
x
lim
=
=
−
+
−
−
+
2
2
3
4
2
2
x
x
x
x
x
∞
→
x
lim
6
2
3
6
=
−
−
x
x
Asymptota uko
ś
na y= x+6
=
−
−
+
=
'
2
2
3
4
)
(
'
x
x
x
x
f
=
−
−
+
−
−
+
2
2
)
2
(
)
3
4
(
)
2
)(
4
2
(
x
x
x
x
x
=
−
+
−
−
−
+
−
=
2
2
2
)
2
(
3
4
8
4
4
2
x
x
x
x
x
x
2
2
)
2
(
5
4
−
−
−
x
x
x
0
>
zawsze dodatni
6
36
=
∆
⇒
=
∆
1
1
−
=
x
5
2
=
x
-1
5
)
;
5
(
)
1
;
(
∞
∪
−
−∞
∈
x
=
−
−
−
=
'
2
2
)
2
(
5
4
)
(
"
x
x
x
x
f
=
−
−
−
−
−
−
−
4
2
2
)
2
(
)
5
4
)(
2
(
2
)
2
)(
4
2
(
x
x
x
x
x
x
=
−
−
−
−
−
−
−
=
4
2
)
2
(
)]
5
4
(
2
)
2
)(
4
2
)[(
2
(
x
x
x
x
x
x
3
=
−
+
+
−
+
−
−
=
3
2
2
)
2
(
10
8
2
8
4
4
2
x
x
x
x
x
x
3
)
2
(
18
−
x
0
>
0
2
>
−
x
2
>
x
)
;
2
(
∞
∈
x
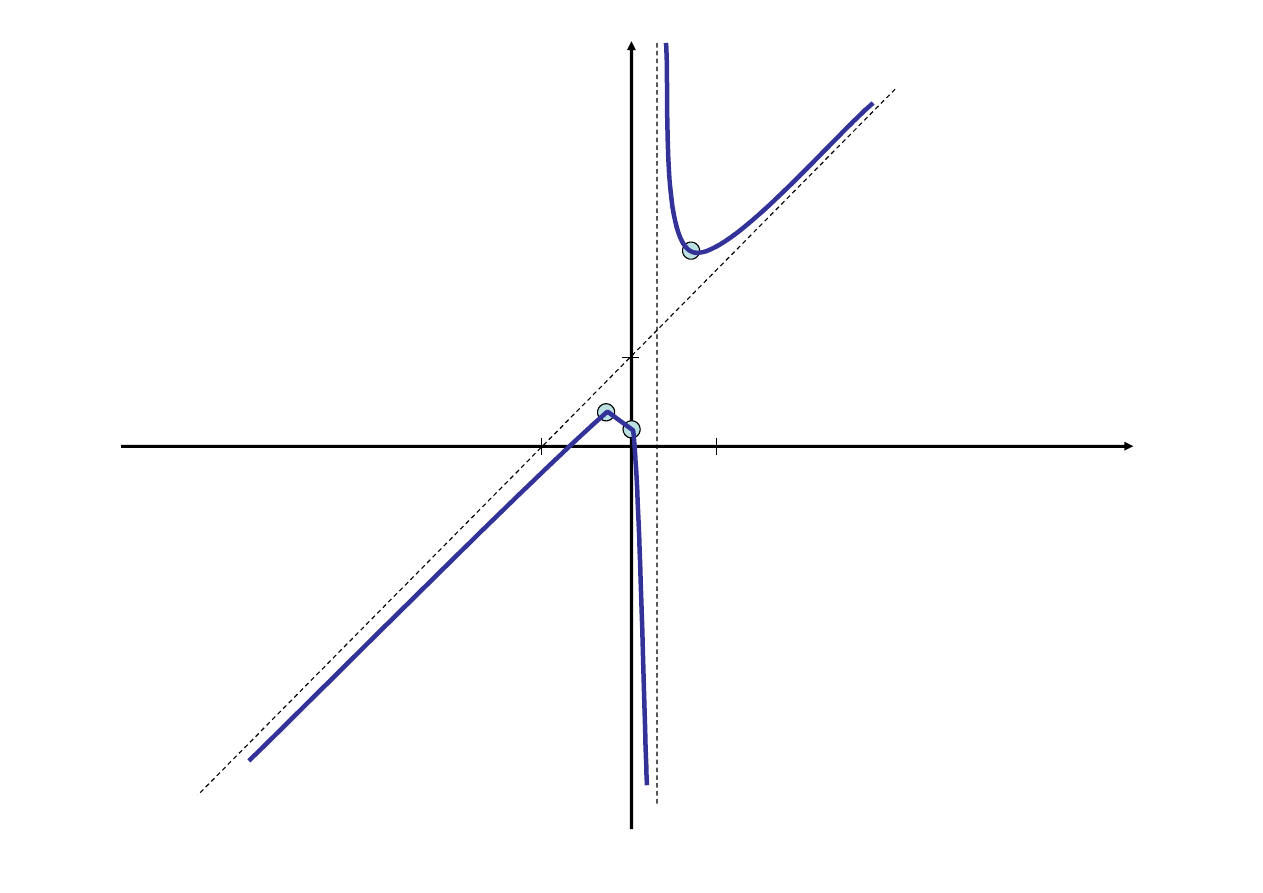
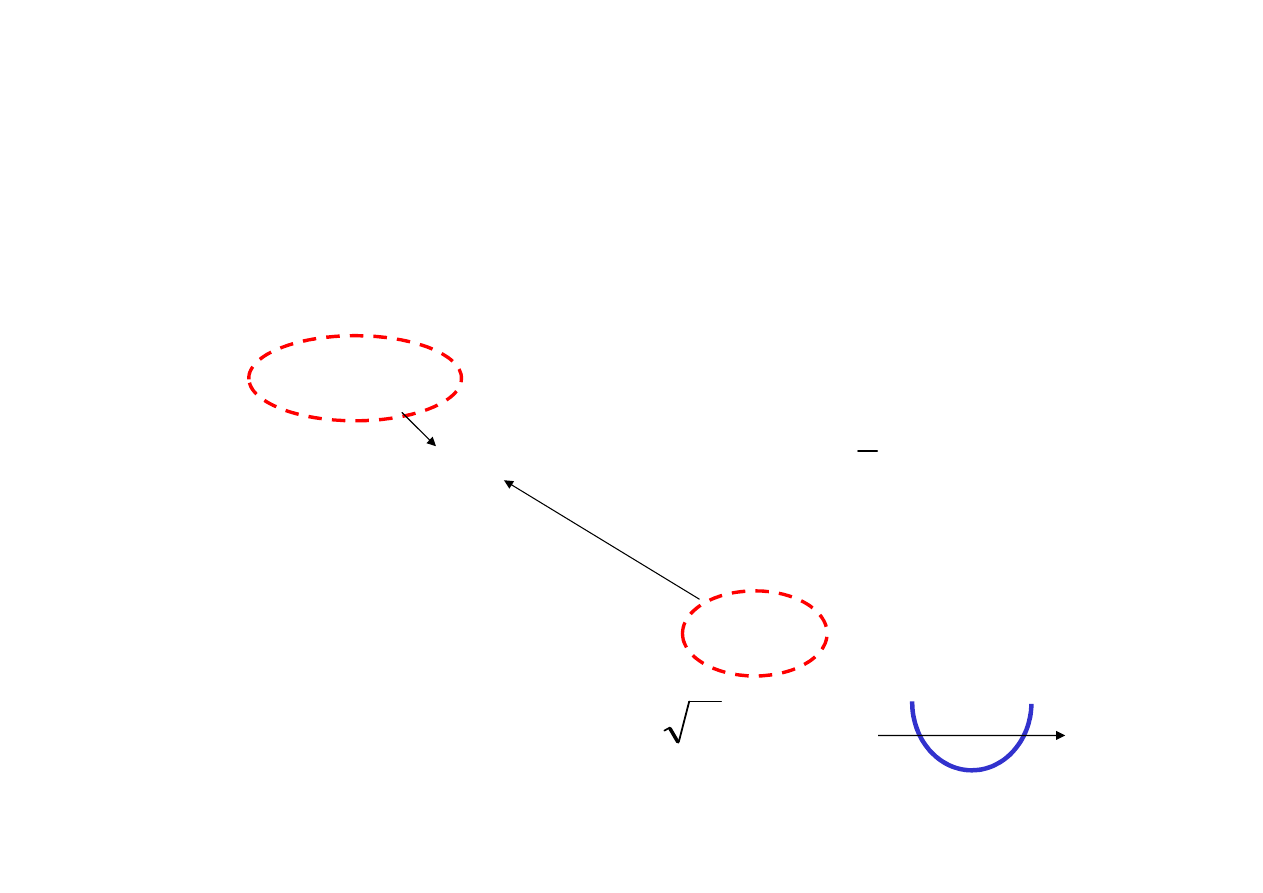
f’(x)
f”(x)
f(x)
-
∞
…
…
∞
…..
…..
…..
-1
2
0
5
X
X
X
+
0
-
0
+
+
+
+
-
-
-
-
-
-
-
-
2
3/2
14
-
∞
-
∞
∞
∞
Maksimum
Minimum
6
-6
9
6
2
2
)
(
−
+
−
=
x
x
e
x
f
R
x
∈
000123
,
0
)
0
(
9
≈
=
−
e
f
)
6
4
(
)
(
'
9
6
2
2
+
−
⋅
=
−
+
−
x
e
x
f
x
x
0
>
−∞
→
x
lim
+∞
→
x
lim
0
=
−
+
−
9
6
2
2
x
x
e
=
−
+
−
9
6
2
2
x
x
e
0
Funkcja posiada asymptot
ę
poziom
ą
y=0
zawsze dodatni
2
3
6
4
<
⇒
−
>
−
x
x
)
6
4
)(
6
4
(
)
(
''
9
6
2
2
+
−
+
−
⋅
=
−
+
−
x
x
e
x
f
x
x
=
−
⋅
+
−
+
−
)
4
(
9
6
2
2
x
x
e
=
−
+
−
+
−
⋅
=
−
+
−
]
4
)
6
4
)(
6
4
[(
9
6
2
2
x
x
e
x
x
)
32
48
16
(
2
9
6
2
2
+
−
−
+
−
x
x
e
x
x
0
>
8
:
/
0
32
48
16
2
>
+
−
x
x
8
:
/
0
4
6
2
2
>
+
−
x
x
2
4
=
∆
⇒
=
∆
2
;
1
2
1
=
=
x
x
1
2
)
;
2
(
)
1
;
(
∞
∪
−∞
∈
x
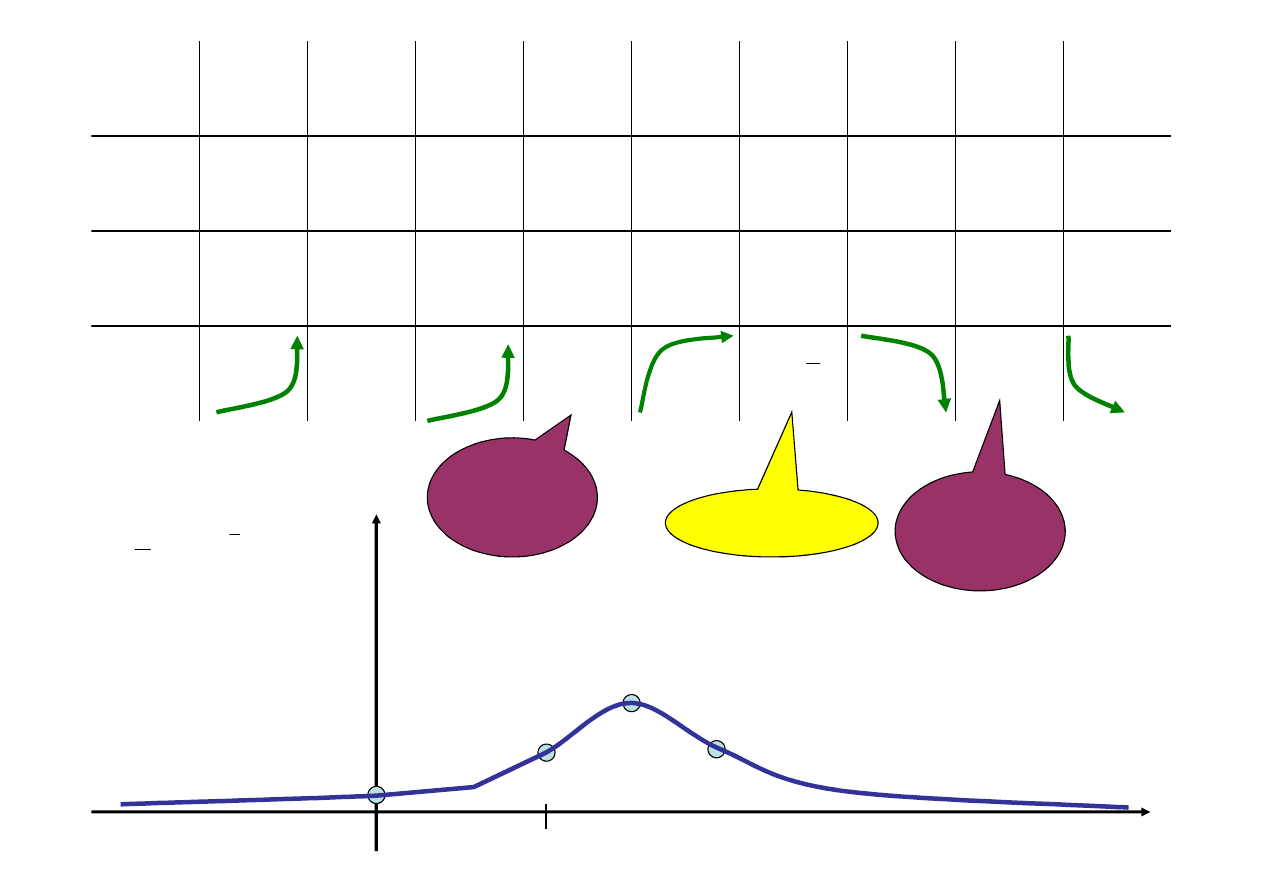
f’(x)
f”(x)
f(x)
-
∞
…
…
∞
0
1
3/2
2
…..
…..
…..
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
0
0
0
0
0
0067
,
0
)
1
(
5
≈
=
−
e
f
0111
,
0
)
(
2
9
2
3
≈
=
−
e
f
0067
,
0
)
2
(
5
≈
=
−
e
f
5
−
e
5
−
e
2
9
−
e
9
−
e
1
Maksimum
Punkt
przegi
ę
cia
Punkt
przegi
ę
cia
Wyszukiwarka
Podobne podstrony:
materialy z zajec 5 id 286508 Nieznany
materialy z zajec 1 id 286505 Nieznany
Materialy pomocnicze 4 id 28534 Nieznany
Materialy oprobowanie(1) id 285 Nieznany
Materialy wybuchowe 2 id 285462 Nieznany
materialy metalowe id 286273 Nieznany
Materialy 5 GLIKOLIZA id 767132 Nieznany
IMIR materialy prad id 211874 Nieznany
Materialy pomocn id 286338 Nieznany
Material teoretyczny id 284375 Nieznany
materialy szkoleniowe 2 id 2863 Nieznany
materialy 10 id 284528 Nieznany
Materialy Pomocnicze (1) id 285 Nieznany
materialy korespondencja id 28 Nieznany
program zajec id 395592 Nieznany
Materialy 8 FERMENTACJI id 7671 Nieznany
Materialy pomocnicze id 285330 Nieznany
Program zajec 2 id 395593 Nieznany
4 materialy pomocnicze id 37744 Nieznany (2)
więcej podobnych podstron