NEUTRON COLLISION THEORY
M. Ragheb
3/30/2006
INTRODUCTION
We wish to analyze the process by which neutrons scatter upon collision with the nuclei of
different materials. The intended use is in shielding, dosimetry, and criticality calculations. The
energy loss per collision would characterize the properties of different energy moderating
materials such as graphite, light water, and heavy water.
The kinematics of two-body collisions processes are best described using the Center of Mass
system (CM), rather than the Laboratory (LAB) system of coordinates. The reason is that
scattering is isotropic in the CM frame, and it is easier described in it.
We then introduce the concept of a microscopic and macroscopic neutron cross section and
describe the use of compiled cross sections data to estimate collision rate densities and reaction
rates.
RELATIONSHIPS BETWEEN VELOCITIES AND ENERGIES IN CM
AND LAB SYSTEMS
The CM system is characterized by:
1.
The total momentum in the CM system is zero.
2.
The magnitudes of the CM velocities do not change in a collision. Their velocity vectors
are rotated through the CM scattering angle.
3.
Cross sections are calculated in the CM system, but are measured and used in the LAB
system.
4.
The total energy in the CM system is always less than in the LAB system. The energy
difference is taken up by the center of mass’ motion itself.
Let us consider:
Mass of target nucleus = A
Mass of neutron = 1
Target nucleus is stationary, implying that
0
V
L
=
We can now deduce the relationships between velocities and energies in the CM and LAB
systems.
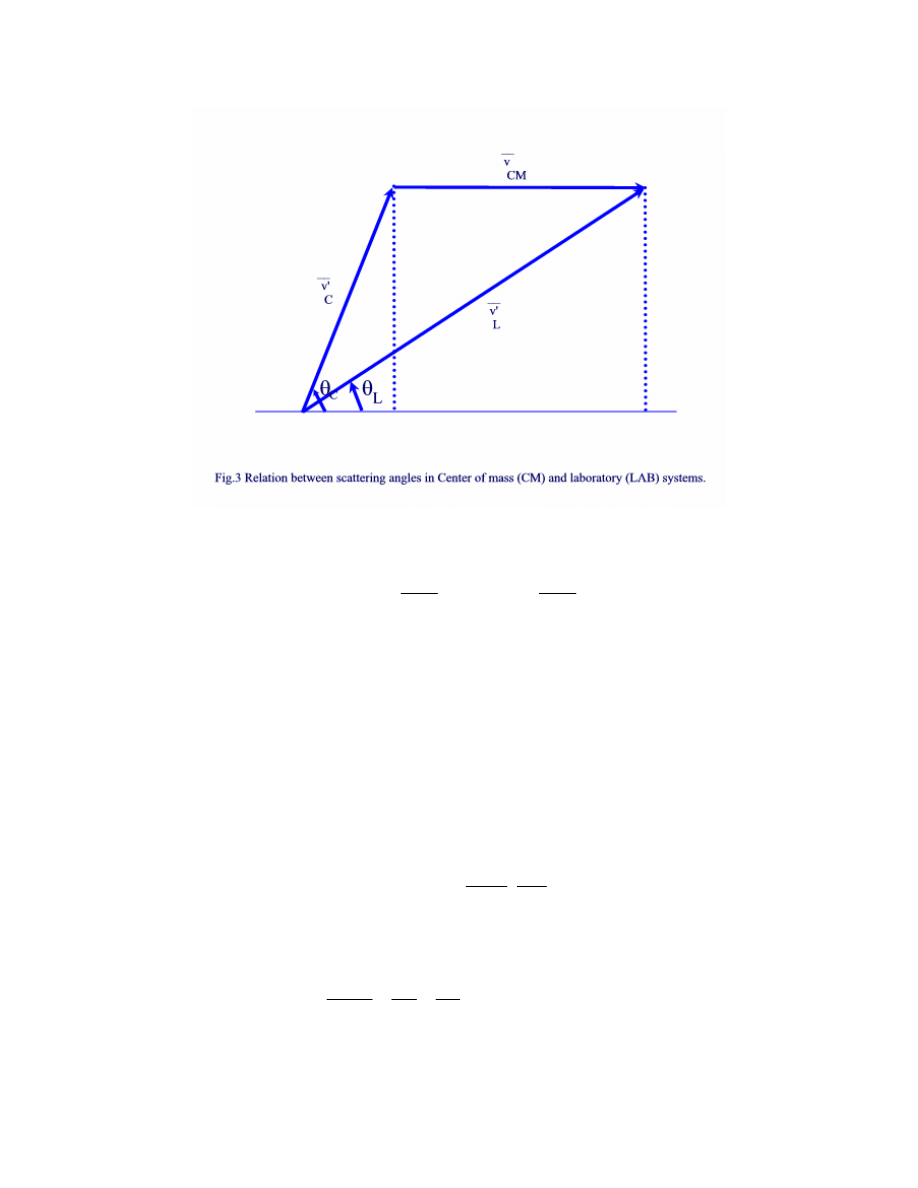
The collision coordinates in the LAB and CM system before and after a collision are shown
in Figs.1 and 2, as well as the relationships between the scattering angles in the LAB and the CM
frames.
The Center of Mass velocity, is obtained by a momentum balance before and after a collision
as:
1
1
CM
L
L
(
A)v
v
A V
+
= ⋅ + ⋅
By taking
L
V = 0, we get:
1
1
CM
L
v
v
A
=
+
(1)
The neutron velocity in the center of mass system using Eqn. 1 is:
1
1
C
L
CM
L
L
v
v - v
v -
v
A
=
=
+
.
From which:
1
C
A
v
L
v
A
=
+
(2)
The target velocity in the Center of Mass system is from Eqn. 1:
1
1
C
L
CM
L
V
V - v
v
A
=
= −
+
(3)
where again we took
L
V = 0.
The total momentum in CM frame is by using Eqns. 2 and 3:
1
1
1
1
C
C
L
L
A
A
v
A V
v -
v
A
A
⋅
+ ⋅
= ⋅
=
+
+
0
The total kinetic energy in the LAB system is:
2
2
1
1
1
2
2
L
L
L
2
1
2
L
E
v
AV
= ⋅ ⋅ +
= v
(4)
where
L
V was taken as zero.
The total kinetic energy in the CM system is:
2
2
1
1
1
2
2
C
C
C
E
v
AV
= ⋅ ⋅
+
Using Eqns.2 and 3 we get:
2
2
2
2
2
2
2
1
1
1
2
1
2
1
1
1
2
1
C
L
L
A
A
L
E
v
v
(A
)
(A
)
A(A
)
v
(A
)
= ⋅ ⋅
+
+
+
+
=
+
Thus:
2
1
1
2
1
2
C
L
A
2
L
E
v
A
v
µ
= ⋅
=
+
(5)
where:
.1
1
A
A
µ
=
+
,
is the reduced mass.
The relationship between the LAB and CM velocities from Eqns 4 and 5 is:
1
C
L
A
L
E
E
A
µ
=
=
+
E
(6)
Thus E
C
< E
L
, since the center of mass motion itself takes the energy difference.
Applying conservation of momentum in the CM system before and after a collision
yields:
Before collision After collision
1
1
C
C
C
C
'
'
v
AV
AV
v
⋅
+
=
+ ⋅
Rewriting this vector equation component-wise in the x and y directions:
cos
cos
'
'
C
C
C
c
C
v
AV
-AV
v
c
θ
θ
−
=
+
(7)
c
0
sin
si
'
'
C
c
C
- AV
v
n
θ
θ
=
+
(8)
Equation 8 implies that:
'
C
v
AV
=
'
C
C
(9)
Substituting in Eqn. 7 we get:
C
v
AV
=
(10)
Then using Eqn. 3 we get:
1
C
A
v
L
V
A
=
+
(11)
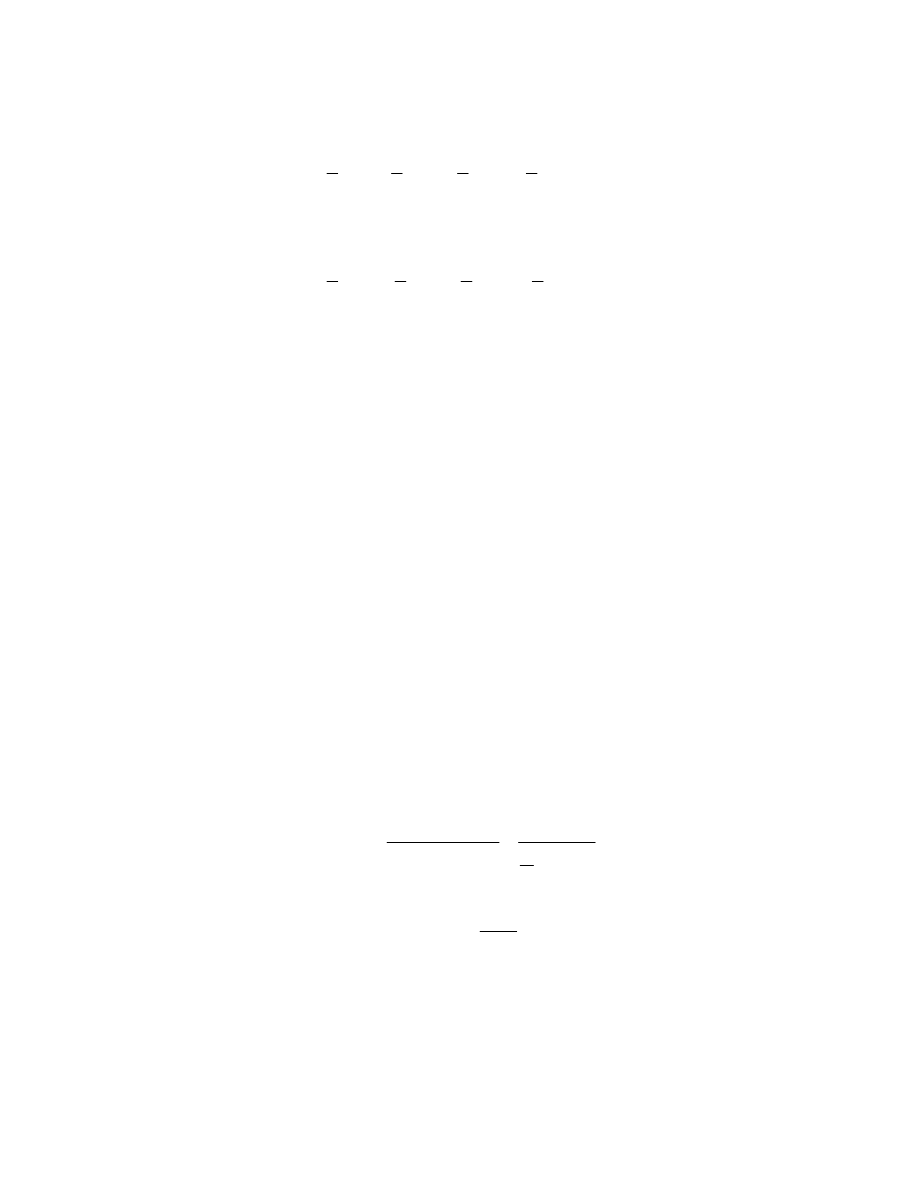
Applying conservation of energy in the CM system yields:
2
2
2
1
1
1
1
.1.
.1.
2
2
2
2
C
C
C
v
AV
v'
AV'
+
=
+
2
C
Substituting for v
c
and v'
c
from Eqns.9 and 10:
2
2
2
2
2
2
2
2
1
1
1
1
2
2
2
2
1
1
C
C
C
C
C
C
A V
AV
A V'
AV'
(A
)V
(A
)V'
+
=
+
+
=
+
which yields:
C
V
V'
=
C
C
'
(12)
Substituting in Eqns. 9 and 10:
C
v
v'
=
(13)
Thus the velocities do not change in the CM frame.
RELATIONSHIP BETWEEN SCATTERING CROSS SECTION IN LAB AND CM
FRAMES
From Fig.3, we can write for the horizontal and vertical components:
Horizontal:
cos
cos
C
'
L
L
CM
v
v
v
C
θ
θ
=
+
(14)
Vertical:
sin
sin
C
'
'
L
L
v
v
C
θ
θ
=
(15)
Dividing the Left Hand Side (LHS) of both equations, we get:
sin
sin
tan
1
cos
cos
C
c
C
L
CM
C
C
C
v'
v
v'
A
θ
θ
θ
θ
θ
=
=
+
+
(16)
Here we used from Eqn.1:
1
1
CM
L
v
v
A
=
+
and from Eqns.2,13:
'
1
C
C
L
A
v
v
v
A
=
=
+
L
C
C
v
A
A
v
v
+
=
=
1
'
Now:
L
L
L
L
CM
C
C
C
(
)sin
d
(
)sin
d
σ θ
θ
θ
σ
θ
θ
θ
⋅
=
⋅
where:
L
L
(
)
σ θ
is the differential scattering cross section in the LAB system,
CM
C
(
)
σ
θ
is the differential scattering cross section in the CM system.
Thus:
C
L
L
CM
C
L
L
sin
d
(
)
(
)
sin
d
C
θ
θ
σ θ
σ
θ
θ
θ
=
⋅
⋅
(17)
From Eqns.15 and 13:
C
L
sin '
'
sin '
L
L
C
C
v
v
v
v
θ
θ
=
=
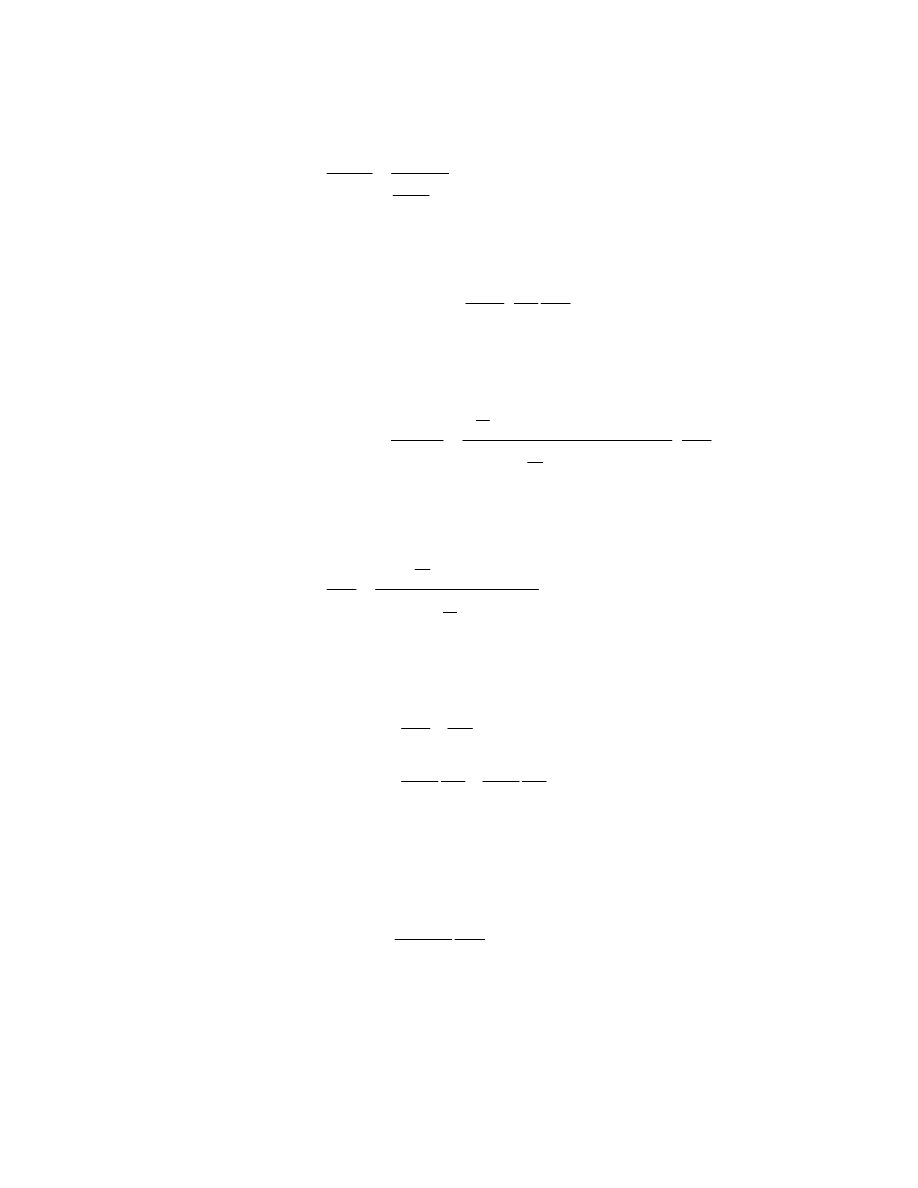
Thus, from Eqn. 11:
C
L
sin '
sin
1
L
L
v
A
v
A
θ
θ
=
+
(18)
Substituting in Eqn.17:
C
L
L
CM
C
L
1 A
' d
(
)
(
)
A
d
L
L
v
v
θ
σ θ
σ
θ
θ
+
=
⋅
⋅
(17)'
Differentiating Eqn.16 with respect to
L
θ , we get:
2
C
C
C
2
C
L
2
2
L
L
C
1
[(
cos
) cos
sin
]
1
d
sec
1
cos
d
(
cos
)
A
A
θ
θ
θ
θ
θ
θ
θ
θ
+
+
=
=
⋅
+
Thus:
2
C
C
2
L
L
C
1
(
cos
)
d
A
1
d
cos
.(
cos
1)
A
θ
θ
θ
θ
θ
+
=
+
(19)
To get an expression for
in terms of
L
θ
2
cos
C
θ
, we use Eqn.14:
2
2
2
'
cos
(
cos
)
'
'
1
(
c
1
'
1
'
CM
C
L
C
L
L
L
L
C
L
L
v
v
v
v
v
A
v
A v
A v
θ
θ
os
)
θ
=
+
=
+
+
+
by use of Eqns. 1, 11 and 13.
Thus:
2
2
2
2
2
1
cos
(1
cos
)
(1
)
'
L
L
L
v
A
A
v
C
θ
θ
=
+
+
(20)
Substituting Eqn.20 into Eqn.19, we get:
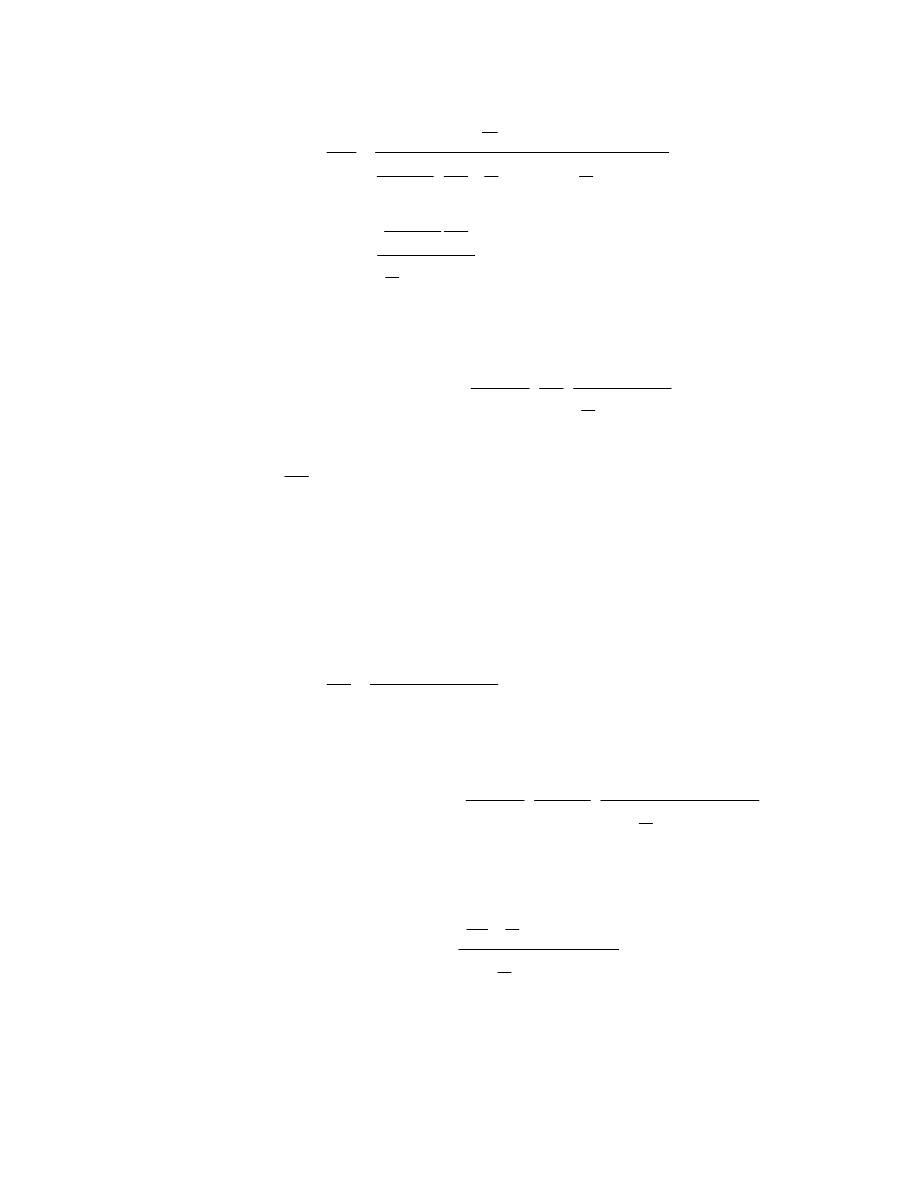
2
C
C
2
2
2
L
C
C
2
2
2
2
2
2
C
1
(
cos
)
d
A
1
1
d
(
cos
) (
cos
1
(1
)
'
(1
)
'
1
(
cos
1)
L
L
L
L
A
v
A
v
A
A
A
v
A
v
A
θ
θ
θ
θ
θ
θ
+
=
)
⋅
⋅
+
+
+
+
=
+
(21)
Substituting Eqn.21 into Eqn. (17)':
3
3
L
L
CM
C
3
3
(1 A)
'
1
(
)
(
)
1
A
(
cos
1)
L
L
C
v
v
A
σ σ
σ
σ
θ
+
=
⋅
⋅
⋅
+
(17)''
To get the value of
3
'
(
)
L
L
v
v
we use the triangular relationship from Fig. 3:
2
2
2
2
2
'
'
2 '
cos(180
)
'
2 '
cos
C
o
L
CM
C
C
CM
C
CM
C
CM
C
v
v
v
v
v
v
v
v
v
θ
θ
=
+
−
−
=
+
+
Substituting for
from Eqn.1, using
CM
v
'
C
v
v
C
=
, and substituting for v
L
from Eqn.11, we get:
2
2
2
'
1
2 cos
(1
)
L
L
v
A
A
v
A
2
C
θ
+
+
=
+
(22)
Substituting Eqn.22 into Eqn. (17)'', we get:
3
2
L
L
CM
C
3
3
(1 A)
1
(1
2 cos
)
(
)
(
)
1
A
(1
)
(
cos
1)
C
C
A
A
A
3 / 2
A
θ
σ θ
σ
θ
θ
+
+
+
=
⋅
⋅
⋅
+
+
Finally:
3 / 2
2
L
L
CM
C
1
2
(
.cos
1)
(
)
(
)
1
(
cos
1)
C
C
A
A
A
θ
σ θ
σ
θ
θ
+
+
=
+
(23)
which relates the scattering cross sections in the LAB and CM systems.
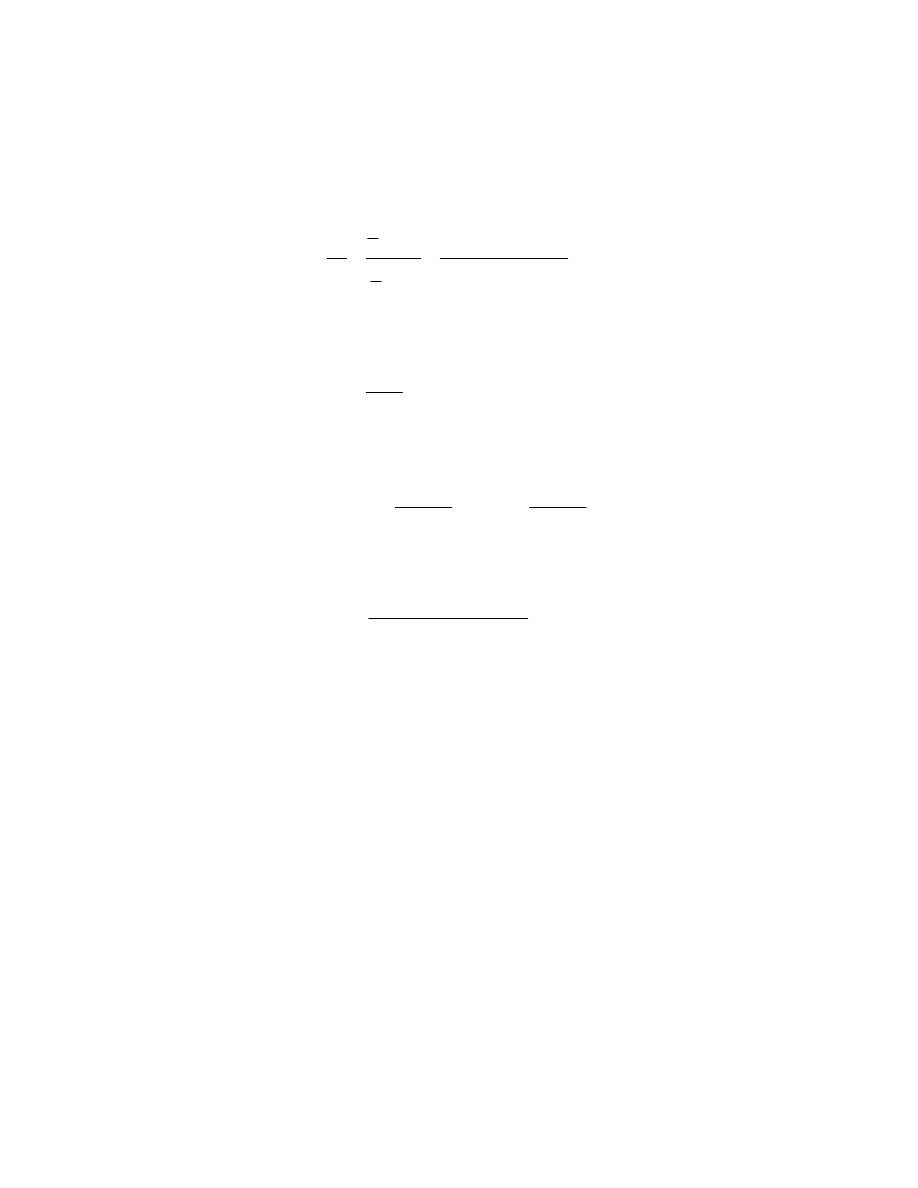
RELATIONSHIP BETWEEN THE INITIAL AND FINAL ENERGIES
To relate the final and initial particle energies in the LAB system, we use Eqn. 22:
2
2
2
2
1
.1. '
'
1 2
2
1
(
1)
.1.
2
L
C
L
v
E
A
A
E
A
v
cos
θ
+ +
=
=
+
(24)
Defining the collision parameter:
2
1
1
A
A
α
−
⎛
= ⎜
+
⎝
⎠
⎞
⎟
(25)
Thus:
2
2
2
1
2
1
2.
, 1-
2.
(
1)
(
1)
A
A
A
A
α
α
+
+ =
=
+
+
And:
(1
)
(1
) cos
'
[
]
2
C
E
E
α
α
θ
+
+ −
=
⋅
(26)
which relates the initial and final energies for a collision.
SPECIAL CHARACTERISTICS OF PARTICLES COLLISIONS ENERGY
TRANSFER
Equation 26 describing the relationship between the initial and final energy of a neutron
after collision with a nucleus possesses several important characteristics:
1. It implies that the energy transfer from neutron to nucleus is related to the scattering angle
in the CM system.
For the case of no collision we have
0
C
θ
= , then:
'
E
E
= .
2. The maximum energy loss occurs in a back scattering collision:
.
180
o
C
θ
=
Then:
'
E
E
α
=
.
The maximum energy loss would be:
max
'
(1
E
E
E
E
E
)E
α
α
∆
= −
= −
= −
3. Not only a neutron cannot gain energy in an elastics collision with a stationary
nucleus (E'<E), but is cannot emerge with an energy E' less than the value of E
α
.
RELATIONSHIP BETWEEN THE SCATTERING ANGLES
C
θ
AND
L
θ
By inspection of Fig.3 we can write using Eqns. 1 and 2:
' cos
' cos
1
cos
1
1
L
L
C
C
CM
L
C
L
v
v
v
A
v
v
A
A
θ
θ
θ
=
+
=
+
+
+
Substituting for v'
L
from Eqn.22, we get:
2
1
(1
2 cos
)
'
(1
)
C
L
L
A
A
v
v
A
θ
+
+
=
⋅
+
/ 2
thus:
2
1/ 2
(1
2 cos
)
1
cos
cos
(1
)
1
1
C
L
C
A
A
A
A
A
A
θ
θ
θ
+
+
=
+
+
+
+
So that:
2
cos
1
cos
(
2 cos
1)
C
L
C
A
A
A
1/ 2
θ
θ
θ
+
=
+
+
(27)
For high mass number elements such as Uranium, A>>1, the second term in the numerator, and
the second and third terms in the denominator are small, then:
2 1/ 2
cos
cos
cos
(
)
C
L
C
A
A
θ
θ
θ
=
≈
and the CM and LAB frames coincide to each other.
THE AVERAGE COSINE OF THE SCATTERING ANGLE
0
µ
We can write in the LAB system:
4
0
0
4
0
cos
cos
L
L
d
d
π
π
θ
µ
θ
Ω
=
=
Ω
∫
∫
where:
2 sin
C
C
d
d
π
θ θ
Ω =
,
is an element of solid angle.
Even though diffusion is isotropic in the CM frame, it is not so, in general, in the LAB
frame.
The departure from isotropic scattering is measured in terms of
0
cos
L
θ
µ
=
, where:
0
0
0
1/ 2
0
1/ 2
0
1
cos
cos
2 sin
4
1
cos
sin
2
1
cos
1
sin
2 ( 2
2 cos
1)
1
cos
1
(cos
)
2 ( 2
2 cos
1)
L
L
C
L
C
C
C
C
C
C
C
C
C
d
d
A
d
A
A
A
d
A
A
π
π
π
π
µ
θ
θ
π
θ θ
π
θ
θ θ
θ
C
θ
θ
θ
θ
θ
θ
=
=
⋅
=
⋅
+
=
⋅
+
+
+
=
+
+
∫
∫
∫
∫
C
C
C
C
C
: cos
,
0
cos
1
1
cos
1
1
Let
y
y
y
θ
θ
θ
θ
π
θ
≡
= ⇒
= + ⇒ =
= ⇒
= − ⇒ = −
+
Thus:
1
0
2
1/ 2
1
1
1
2
1/ 2
2
1/ 2
1
1
1
1
2
(
2
1)
1
1
2
(
2
1)
(
2
1)
Ay
dy
A
Ay
Ay
dy
dy
A
Ay
A
Ay
µ
+
−
+
+
−
−
+
=
+
+
⎡
⎤
=
+
⎢
⎥
+
+
+
+
⎣
⎦
∫
∫
∫
Now, from a table of integrals:
2
2
2(2
,
3
dx
a
bx
xdx
a
bx
a
bx
b
b
a
bx
a
bx
+
− )
=
= −
+
+
+
∫
∫
Thus:
1
2
2
2
0
2
1
2
2
2
0
3
2
2
3
2
2
2 (
1)
2
1
( 2)[2(
1)
2
]
(
1)
2
2
12
2
:
A
1,
2A
1
1
(
1
)(
1)
(
1
)(
1)
(
1)
(
1)
2
3
1
1
(
1
1
2
3
1
2
A
Ay
A
A
Ay Ay
A
Ay
A
A
where
b
A
A A
A
A A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
µ
α
µ
+
−
⎡
⎤
+ +
−
+ −
=
+ +
+
⎢
⎥
⎢
⎥
⎣
⎦
≡
+
≡
⎡
⎤
⎡
⎤
=
−
+ −
+ −
+ +
−
+
+ −
−
⎣
⎦
⎢
⎥
⎣
⎦
⎡
⎤
⎡
⎤
=
−
+ −
+
+ − −
− −
+
+ +
+
⎣
⎦
⎢
⎥
⎣
⎦
=
)
2
2
1 6
2
2
2
3
2
3
3
A
A
A
−
⎡
⎤
− +
=
=
⎢
⎥
⎣
⎦
(28)
This relationship applies for elements other than hydrogen, that is for A not equal to unity.
THE SCATTERING PROBABILITY DISTRIBUTION FOR ELASTIC
SCATTERING FROM STATIONARY NUCLEI
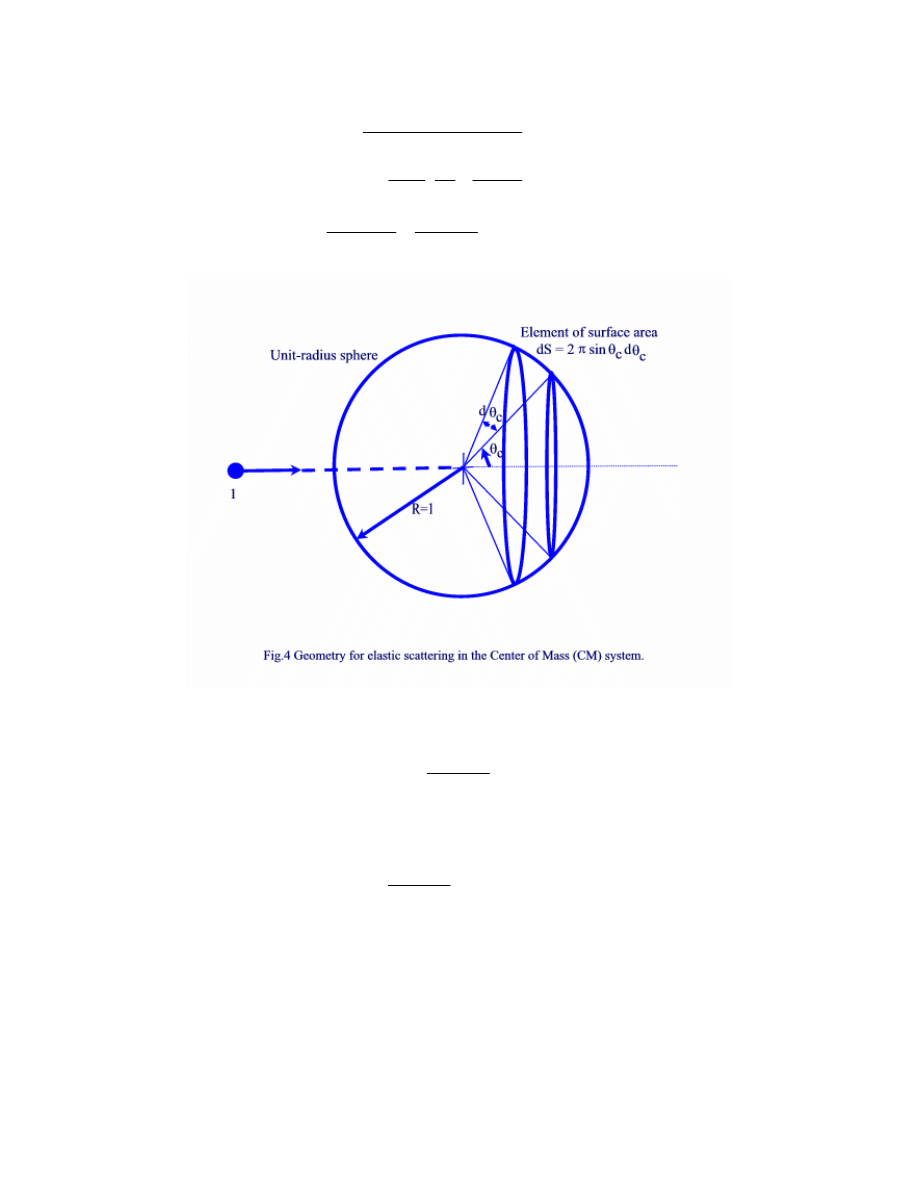
Since scattering is isotropic in CM system, the probability:
C
C
( ')
'
Number of favorable events scattering between
and
d
P E dE
Total number of events
C
θ
θ
θ
+
=
,
can be expressed using Fig. 4 as:
2
( ')
'
2 sin
4
1
(cos
)
'
2
'
1 (cos
)
'
2
'
C
C
C
C
Surface dS
P E dE
Total unit surface
d
d
d
dE
d
dE
dE
π
θ θ
π
θ
θ
=
=
⋅
= −
⋅
= −
⋅
E
From Eqn. 26:
(1
)
(1
) cos
'
2
2
'
(1
)
cos
1
(1
(cos
)
2
'
(1
)
C
C
C
E
E
E
E
d
dE
E
)
α
α
θ
α
θ
α
α
θ
α
+
+ −
=
⋅
+
=
⋅
−
−
−
=
−
Thus:
1
( ')
'
'
(1
)
P E dE
dE
E
α
= −
⋅
−
(29)
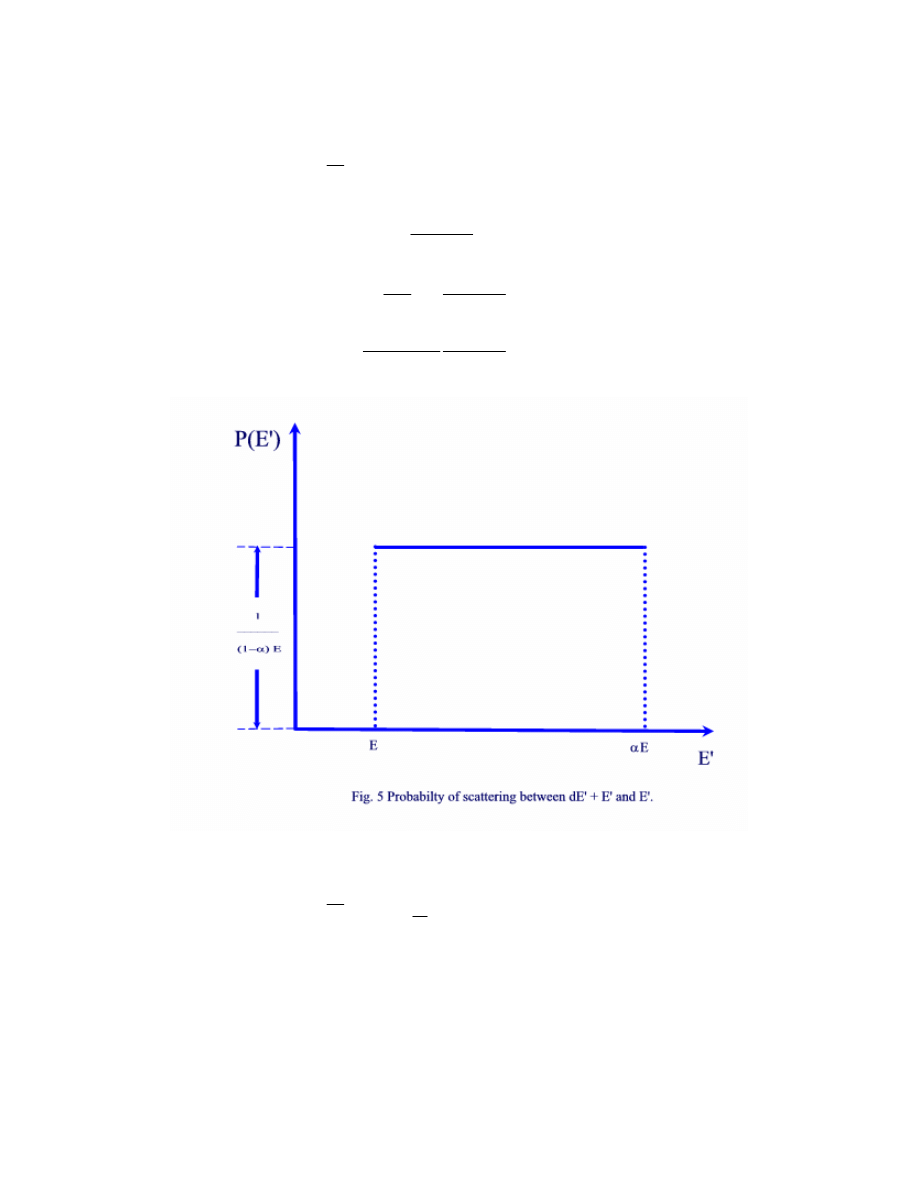
Since dE' is negative, P(E') is positive and equal to:
1
( ')
(1
)
P E
E
α
=
−
and the collided neutron energy will be between E and E
α
. This is shown in Fig.5. The neutron
has an equal probability of falling between the energies E'=E and E'= E
α
.
AVERAGE ENERGY OF NEUTRON AFTER A COLLISION
This, using Eqn. 29 can be written as:
2
2
2
2
'
' ( ')
'
1
'
'
(1
)
'
1
.
2
(1
)
1
2
(1
)
E
E
E
E
E
E
E
E P E dE
E
dE
E
E
E
E
E
E
α
α
α
α
α
α
α
=
= −
−
⎡
⎤
= − ⎢
⎥
−
⎣
⎦
−
=
−
∫
∫
Thus:
'
(1
)
2
E
E
α
= +
(30)
THE AVERAGE LOGARITHMIC ENERGY DECREMENT PER
COLLISION
The average value of decrease of the natural logarithm of neutron energy in a collision is:
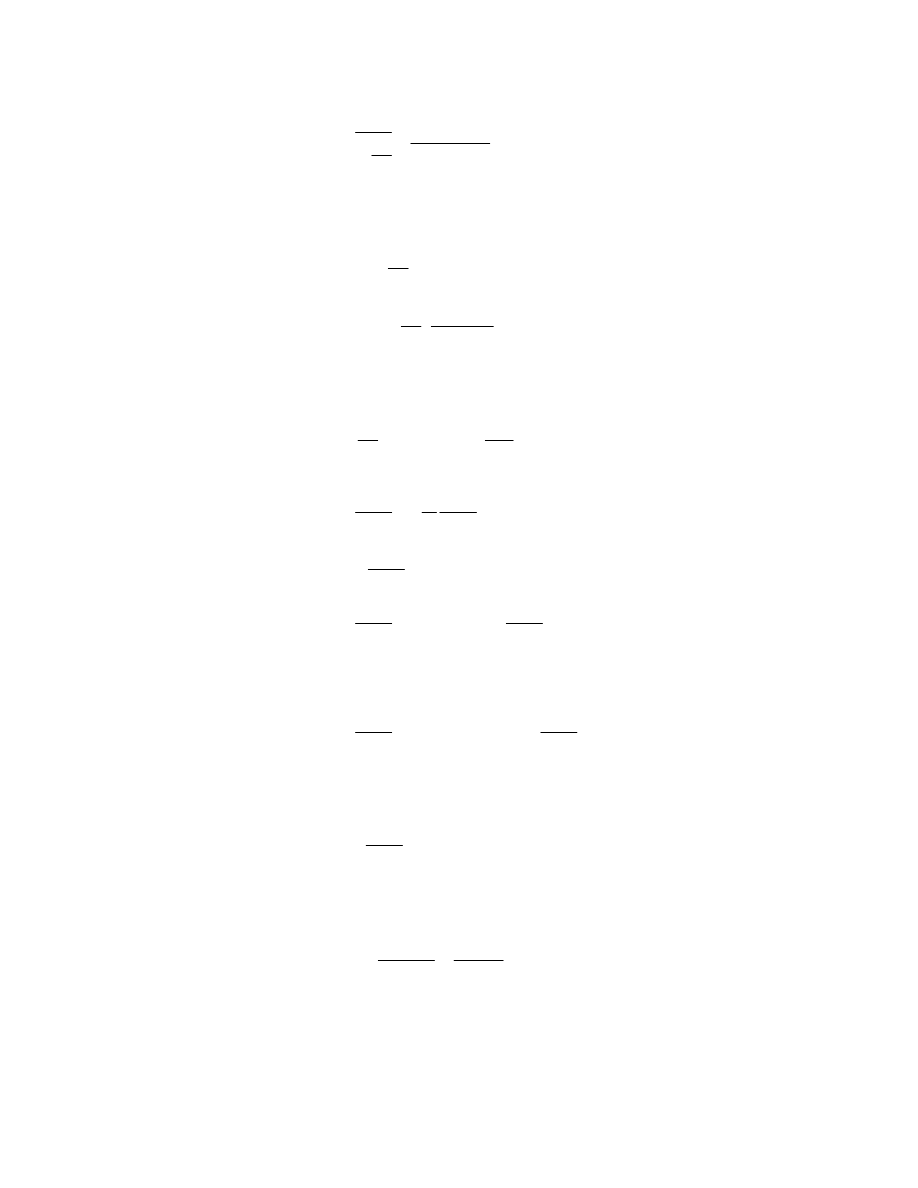
ln
ln
ln
'
'
E
E
E
E
ξ
=
=
−
(31)
Its utility is that it is independent of the neutron energy as shown below:
ln
( ')
'
'
'
ln
' (1
)
E
E
E
E
E
P E dE
E
E
dE
E
E
α
α
ξ
α
=
= −
⋅
−
∫
∫
Making the change of variable:
'
'
E
dE
d
E
E
χ
χ
=
⇒
=
1
1
1
1
1
ln
1
1
ln
1
1
1
[ ln
]
[ ln
1]
1
1
Ed
E
d
α
α
α
χ
ξ
α
χ
χ χ
α
χ χ χ
α α α
α
α
−
=
−
= +
−
=
−
=
−
−
−
∫
∫
+
From which:
1
[1
ln ] 1
ln
1
1
α
ξ
α α α
α
α
=
− +
= +
−
α
−
(32)
But the collision parameter is:
2
1
1
A
A
α
−
⎛
⎞
= ⎜
⎟
+
⎝
⎠
Thus:
2
(
1)
(
1
1
ln
2
(
A
A
A
A
ξ
)
1)
−
−
= +
+
(33)
When A is large, (A>>1), for heavy elements:
2
3
5
3
5
(
1)
1
1
1
1 2
[
...]
2
3
5
1
1
1
1
: ln(
)
2(
...)
1
3
5
A
A
A
A
A
Z
Since
Z
Z
Z
Z
ξ
−
→ −
+
+
+
+
≈
+
+
+
−
2
2
2
1
2
1
A
A
A
A
ξ
−
+
= −
≈
(34)
by considering that the value of 1 in the numerator is small relative to the other terms.
For A>10 an expression correct to about 1% fitting experimental data is:
2
2
3
A
ξ
=
+
(35)
In the case of mixture of elements in a moderator, the individual values of
ξ
are weighed
by the scattering cross sections of each component to obtain its average value over the mixture:
1
1
n
si i
i
n
si
i
σ ξ
ξ
σ
=
=
=
∑
∑
(36)
THE AVERAGE NUMBER OF COLLISIONS IN A MODERATOR
To slow down from energy
'
'
E E to energy
''
E
'
'
E the number of neutron collisions can
be estimated from:
'
ln
''
E
E
N
ξ
=
(37)
SLOWING DOWN POWER AND MODERATING RATIOS
These moderator parameters are defined as:
Slowing down power =
s
ξ
∑
(38)
This is a measure of how efficient a material is in slowing-down the neutron energy.
Moderating ratio =
s
a
ξ
∑
∑
(39)
This is a measure of the efficiency of moderation without absorption.
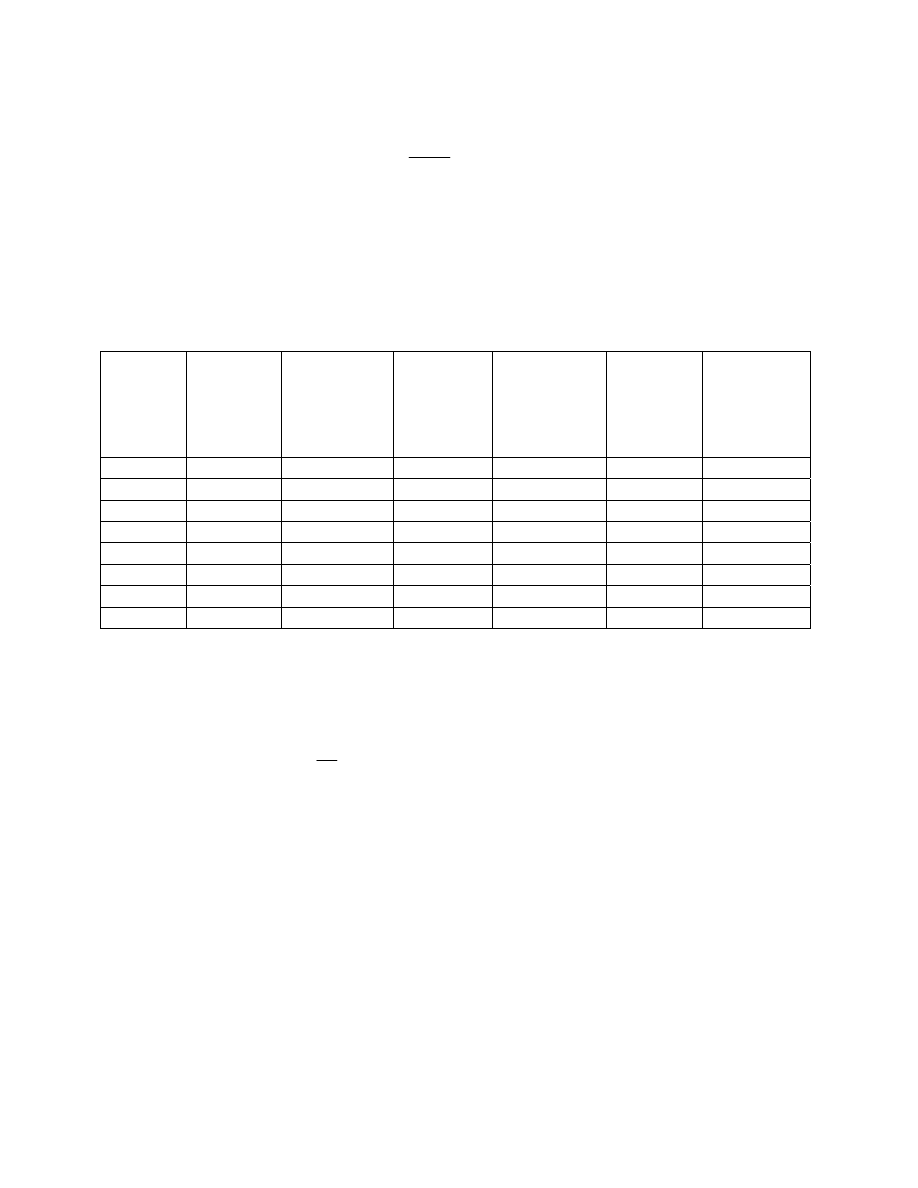
Table 1 compares the values of the slowing down power and the moderating ratios for
several materials. Deuterium used in heavy water distinguishes itself as a superior moderator.
Nevertheless, carbon as graphite, light water and beryllium are also used as neutron moderators.
Table 1: Properties of major moderator materials.
Element
Mass
Number
A
Average
Logarithmic
Energy
decrement
ξ
Average
Number
of
Collisions
N
Macroscopic
Absorption
Cross
section
Σ
a
Slowing
Down
Power
ξΣ
s
Moderating
Ratio
ξΣ
s
/
Σ
a
H
1 1 18
0.0792
1.53
72.0
D
2 0.725 25 0.0009
37.0
12,000.0
He
4 0.425 43 0.0
0.000016
83.0
Li
7 0.268 67 71.0
0.176
159.0
Be
9 0.209 80 0.008 -
-
B
11 0.176 103 780.0 - 170.0
C
12 0.158 115 0.005
0.064 -
O
16 0.120 150 0.0
-
-
THE LETHARGY OR LOGARITHMIC ENERGY DECREMENT
This is defined as:
0
ln
E
u
E
=
(40)
where
is arbitrary reference energy corresponding to zero lethargy (e.g. 10 MeV).
0
E
The lethargy of a neutron increases as it is slowed down. The lethargy variable allows the
expression of the neutron energy E as a dimensionless variable.
The lethargy change can be written as:
1
2
1
2
ln
E
u
u
u
E
∆ =
− =
(41)
From Eqn. 40:
0
u
E
E e
−
=
(42)
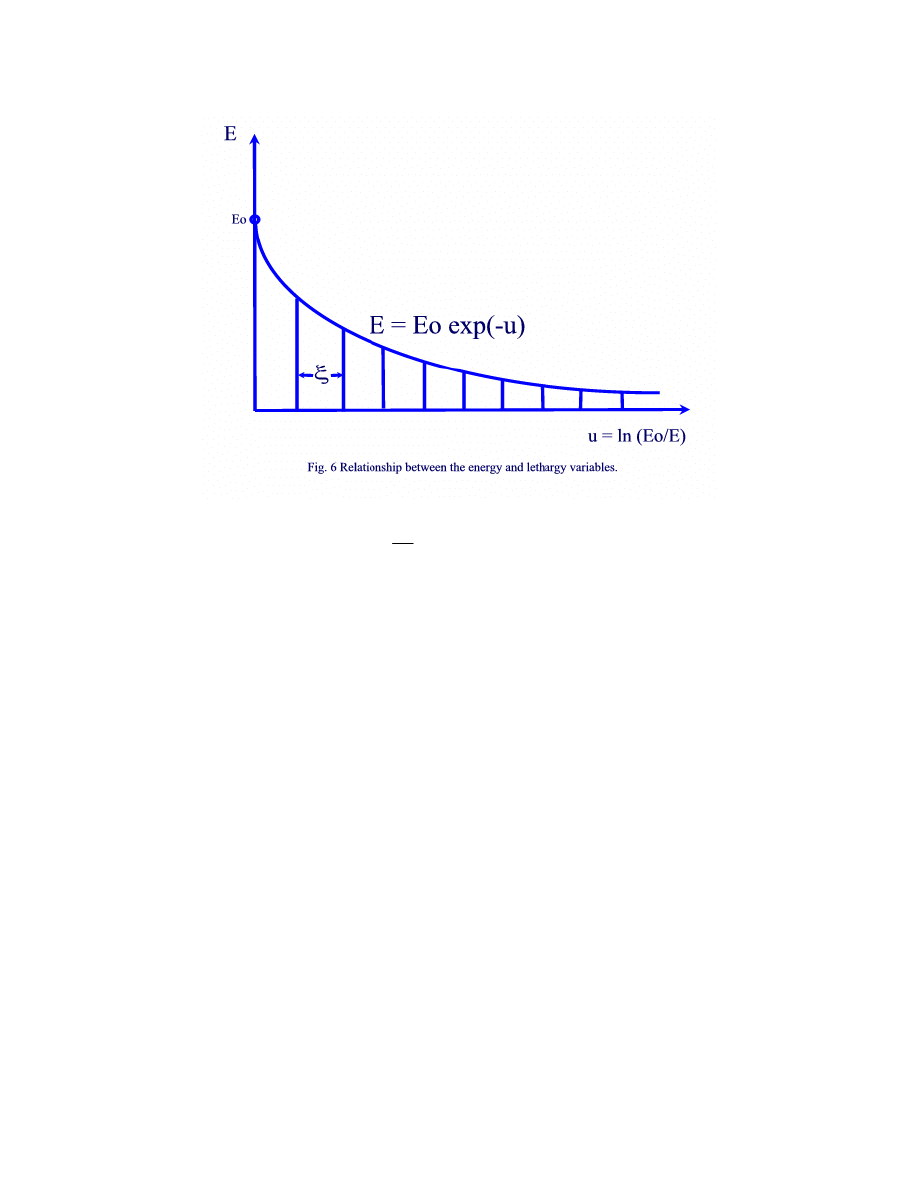
It is evident that
ξ
can be regarded as the average change in the lethargy of a neutron per
collision. Regardless of its energy, a neutron suffers the same number of collisions for the same
specified change in lethargy. Figure 6 shows that a neutron loses considerably more energy in
earlier scatterings than in later ones.
REFERENCE
1. M. Ragheb, ”Lecture Notes on Fission Reactors Design Theory,” FSL-33, Department of
Nuclear, Plasma and Radiological Engineering, 1982.
EXERCISE
1.
Carry out the detailed derivation proving that, for elements other than hydrogen, the
mean value of the cosine of the scattering angle for neutron collisions is given by:
4
0
0
4
0
cos
2
cos
3
L
L
d
A
d
π
π
θ
µ
θ
Ω
=
=
=
Ω
∫
∫
.
Document Outline